基于时间反转变换的动目标相参积累算法*
刘海涵,吕卫祥
(南京船舶雷达研究所724所,江苏 南京 211106)
0 引言
在现代战争中,雷达面临的目标日趋复杂,主要体现在低雷达反射截面积(radar cross section,RCS)、高速度和高机动3个方面[1]。在不增加硬件成本的条件下,采用长时间相参积累算法提高信噪比,实现微弱目标检测与识别具有非常重要的军事意义[2-3]。而如何解决长时间积累过程中存在的三跨问题:跨距离单元、跨多普勒单元、跨波束也成了国内外学者的研究热点[4]。
包络补偿和相位补偿是实现长时间相参积累的关键[5]。针对匀加速度高速机动目标,常采用不需要先验速度信息的Keystone[6]变换及其高阶形式实现距离走动和距离弯曲的校正。在包络对齐后,根据目标的运动特性将目标信号沿方位向的分布建模为QFM(quadratic frequency modulated)信号并采用时频变换或构建匹配项多维搜索的方法对其进行参数估计[7]。近年来结合Radon[8]变换和Key‑stone变换的包络与多普勒统一补偿的算法较为流行。典型算法有:广义拉东傅里叶变换[9](generalized Radon Fourier transform,GRFT)、Keystone分数阶 傅 里 叶 变 换[10](KT-fractional Fourier transform,KT-FRFT)、Radon线性正则变换[11](Radon linear ca‑nonical transform,RLCT)等。以上几种算法都无法避免多维搜索。随着信号采样点数及积累脉冲数增加,算法运算量陡升,给硬件设备带来巨大压力,不利于雷达对目标的实时检测。
2016年李小龙提出TRT-SKT-LVD(time revers‑ing transform,second-order Keystone transform and LV′s distribution)算法[12]。该算法无需搜索,极大降低了运算量,且拥有较优的检测性能。但在慢时间维对回波进行反转相乘简化信号模型时会丢失目标的速度信息。导致多目标拥有相同的距离和加速度时算法失去分辨能力,严重制约了该算法的应用范围。
本文提出TRT-KTR(time reversing transform,first-order Keystone transform and Radon transform)算法,在慢时间维对回波进行反转相除,剥离出目标的速度信息。针对相除运算产生的噪声突变点,采用低通滤波器和线性平滑法消除其影响。并采用Keystone变换校正目标速度引起的距离徙动。利用Radon变换估计速度模糊数并进行补偿实现回波能量的相参积累。TRT-SKT-LVD与TRT-KTR相配合,克服了其不能测速的缺陷,能够实现多目标检测。联合算法运算复杂度没有增加,且2个算法采用分段并行运算有利于减少硬件设备的负担,提高信号检测的实时性。
1 信号模型
假设雷达发射线性调频信号(linear frequency modulated,LFM)[13]如下:

式中:γ为线性调频信号调频斜率;Tp为脉冲宽度;fc为雷达载频;τ为快时间;tm=m⋅PRT代表慢时间,m=-(N-1)/2,…,-1,0,1,…,(N-1)/2,N为 积累脉冲数,PRT为脉冲重复时间;rect(·)为矩形函数。
假设|v|/c≪1,c为光速。雷达接收到的基带信号为

式中:σ0为雷达反射系数;λ=c/fc为雷达波长。
对信号进行脉冲压缩得

式中:A为信号脉压后幅值;B为信号带宽。对于匀加速直线运动目标:

式中:R(tm)为动目标到雷达的距离;R0为初始距离;v为目标径向速度;a为目标径向加速度。
当目标运动速度过快而雷达的脉冲重复频率PRF较低时,在方位向会发生多普勒欠采样。此时目标的径向速度可表示为[14]

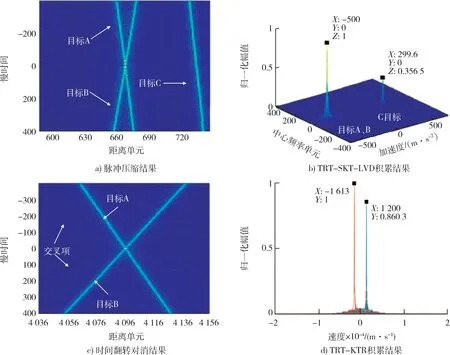
式中:vamb=PRF⋅λ/2表示盲速;|v0| 对式(2)沿快时间τ作傅里叶变换,并将式(6)带入: 式(7)存在4个相位项,前3个相位项分别包含目标的运动参数:初始距离、初始速度和加速度。从后计的3个相位项中,快时间频率fτ皆与慢时间tm相耦合,其中速度v0、速度模糊数F所在相位项为一阶耦合会造成线性距离走动。而加速度所在相位项为二阶耦合会造成距离弯曲。 对式(7)沿慢时间维作时间反转变换得 用(tm,fτ)乘S(tm,fτ)得 由式(9)知TRT变换后,信号的速度信息因相乘对消而丢失。这导致TRT-SKT-LVD算法无法测速。 对式(9)作二阶Keystone变换(SKT),令 代入式(9)并沿快频率维作逆傅里叶变换得 由式(11)可知,完成二阶Keystone变换校正距离弯曲后,信号快时间维峰值均落在4R0/c对应的距离单元内。取峰值所在距离单元内的慢时间信号: 对式(12)采用LVD[15]变换得 式中:γ为调频斜率单元。由式(13)知,通过估计调频斜率单元峰值位置即可得到目标加速度。 令D(tm,fτ)=S(tm,fτ)/Sˉ(tm,fτ),又因为 exp(-j4πfcFvambtm/c)=1,得 对式(14)进行一阶Keystone变换,令 代入式(14)得 在窄带雷达条件下,fτ≪fc,得 式(16)改写为 采用Radon变换估计模糊数F。由式(17)知在一阶Keystone变换后模糊速度会造成线性距离走动。在快时间维-慢时间维平面脉压峰值表现为一条斜线。沿不同角度对式(17)作Radon变换,当与峰值斜线角度相同时,Radon变换得最大值,得到估计角度̂,可求得速度模糊数F=tan̂(fc/fs)。 构建匹配项exp(j8πfτFvambtn/λfc)对式(16)进行补偿后得 对式(19)沿fτ作逆傅里叶变换后再沿慢时间作傅里叶变换得 式中:fn为多普勒频域,通过估计多普勒频域单元峰值的位置即可得到目标速度。 假设回波中存在高斯白噪声,时间反转相除运算会产生突变点。突变点可分为2类:一种是幅值接近于0的下突变点;另一种是幅值远大于回波最大幅值的上突变点。下突变点出现位置可视为该点信号缺失。由式(14)已知,时间反转变换后的信号产生线性距离走动。缺失部分数据点的信号虽然会损失部分信号能量;但回波矩阵仍会保持包络走动的线性特征,后续Radon变换和相参积累的峰值位置并不会受到影响。这种损失可以通过增加脉冲积累数量延长积累时间减轻其影响,一般来说是可以接受的。 假设在tm=t′时共产生了k个上突变点,其幅值为(M1,M2,…,Mk)≫max(D(tm,fτ)),此时TRT相除后的信号可写为 沿快频率维对式(21)作逆傅里叶变换得 由式(22)可知,在慢时间为t′时的快时间域,上突变点的存在会导致快时间域内回波能量整体大幅抬升,进而导致相参积累后信号与噪声能量的归一化比值大幅降低。在后续Radon变换中,上突变点造成的慢时间能量整体抬升,会在搜索角度90°位置产生伪峰,严重干扰速度模糊数的估计。对此采用低通滤波器加线性平滑法减少上突变点的影响。 由式(14)可知,由于门限函数rect(fτ/B)的限制,D(tm,fτ)是以带宽为B的低通信号。采用低通滤波器,保留通带内的信号,尽量压低有效带宽以外的突变点。对滤波后的信号Dh(tm,fτ),设置参考门限L,L≥max(D(tm,fτ))。设置参考单元数为m,m为偶数。沿快时间维遍历,当离散点值大于门限L则被判断为突变点。在这个点左右各寻找最近的m/2个非突变点,即参考单元,并将突变点赋值为m个非突变点的均值。通过线性平滑,消除突变点的影响。 当回波中存在多个目标时,慢时间反转变换不可避免地产生交叉项,且目标越多交叉项越多,影响越严重。由式(13),(20)可知,TRT-SKT-LVD算法可以积累出目标加速度与距离信息。TRT-KTR算法可以积累出目标速度信息。相参积累完成后,2个算法得到的信息是独立的。当回波中存在多目标时,需要对目标参数进行匹配。 在实际应用中,雷达所探测的目标距离、速度、加速度最大范围是已知的。目标积累时间内在快时间域产生的距离走动是有限的。本算法中根据雷达系统先验信息,采用将脉压后的数据在快时间维上分段并行处理的策略来减少信号间交叉项。 快时间维分段如图1所示,存在A到F 6个目标。假设动目标脉压峰值最大走动距离不超过2个网格。不分段情况下,图1中所有目标在慢时间反转变换后会相互耦合并产生交叉项。分段后,C被截断。A,B为一组,D,E,F为一组。对不同分段单独作慢时间反转变换后,A,B间产生交叉项,D,E,F间产生交叉项,大大减少了交叉项的数量。C因为被截断,能量损失严重,对A,B影响较小。对脉压信号重新分段后C在段内保持连续,目标运动特征完整保留,利于后续检测。脉压后信号分段并行处理减少了单次计算的距离单元数,降低单次运算数据量,有利于信号实时检测。 图1 快时间维分段示意图Fig.1 Fast time dimension segmentation diagr am 本算法中以段为单位,采用帧间动目标跟踪的方法进行目标参数匹配。目标的运动状态已知为匀加速度直线运动,在运动过程中加速度保持不变。令一个慢时间积累周期的数据矩阵为一帧,在相邻帧中,经过TRT-SKT-LVD算法处理可得多组相关联的距离与加速度。经过TRT-KTR算法处理可得多组速度。根据匀加速度运动模型,由于帧间时间间隔为已知固定值,故相邻帧同目标速度增量由其加速度确定。计算不同速度对应的走动距离,根据速度增量和走动距离联合求解线性方程组,可将目标参数匹配。在实际工程应用中,径向多目标分辨时具有相同距离单元与相同加速度的目标数不会过多。当具有相同距离单元与相同加速度的目标数不超过2时,单帧信息即可实现目标参数匹配。 联合算法流程图如图2所示。 图2 TRT-SKT-LVD与TRT-KTR联合算法流程图Fig.2 Flowchart of TRT-SKT-LVD and TRT-KTR joint algorithm (1)对雷达接收到的信号进行去载频得到基带信号sr(tm,τ),进行脉冲压缩得到s(tm,τ)。 (2)对s(tm,τ)快时间维作傅里叶变换得s(tm,fτ),并作慢时间翻转变换得Sˉ(tm,fτ)。 (3)S(tm,fτ)与Sˉ(tm,fτ)相除得D(tm,fτ),通过低通滤波器进行频域滤波。低通滤波器通带带宽与发射信号一致。 (4)设定参考门限L,滤波后的信号沿快频率维fτ进行遍历,对于超过参考门限的值视为突变值,取相距最近的m个参考单元的均值代替突变值。 (5)对进行门限平滑后的信号D′(tm,fτ)进行一阶Keystone变换得D′(tn,fτ)。 (6)对D′(tn,fτ)采用Radon变换估计模糊数F,构建匹配项exp(j8πfcFvambtn/c)进行补偿。 (7)对补偿后的D″(tn,fτ)沿fτ作逆傅里叶变换后再沿慢时间tn作傅里叶变换积累出目标。 假设积累脉冲数为M,距离单元数为Nr,多普勒模糊搜索个数为NF,单位慢时间平均突变点个数为Nc个。 时间反转变换需要进行MNr+2MNrlbNr复数乘法。频域滤波需要进行MNr次复数乘法,平滑突变点需要2MNc次复数乘法。采用Chrip-Z算法实现Keystone变换,需要12MNr+2MNrlbNr次复数乘法。Radon变换与补偿模糊速度共需要进行MNF+MNr次复数乘法。慢时间FFT积累速度v需要进行MNrlbM。当M=Nr=NF=Nc时,TRT-KTR算法计算复杂度为O(N2lbN);TRT-SKT-LVD算法计算复杂度为O(N3lbN)[12];联合算法计算复杂度依然为O(N3lbN),计算复杂度并未增加。相较于GRFT的计算复杂度O(N5),小了近2个数量级。 为了验证算法的有效性,雷达仿真参数如表1所示。假设初始时刻目标与雷达的距离R0=50 km,径向速度v0=1 200 m/s,径向加速度a0=300 m/s2做匀加速直线运动。在无噪声条件下,单目标仿真结果如图3所示。 表1 雷达系统参数Table 1 Radar system par ameters 图3 a)为脉冲压缩结果。积累期间回波发生严重的距离走动,走动16个距离单元。由表1得距离分辨率为ΔR=c/2fs=15 m。在慢时间序号为-200时目标速度为v′=1 170 m/s。理论距离走动单元数为RM=(v′t+0.5a0t2)/ΔR=16。仿真与理论吻合。 在慢时间序列号为0时对应脉压峰值的距离单元为R0/delta_R≈3 333。Radon变换搜索峰值所得脉压倾斜角为175.4°,动目标速度模糊数估计值为Fest=(fc/fs)tan(θπ/180)=-80.5。由式(17)知TRT后模糊数扩大了2倍。理论模糊数为-40,模糊数估计误差为0.006 25。图3 c)为Keystone变换并补偿了速度模糊数后,不同慢时间回波的脉压峰值落在同一距离单元,距离走动被校正。图3 d)为相参积累结果,速度分量被积累起来形成峰值。图3的仿真结果与理论保持一致,所提算法能准确估计模糊数,并有效实现目标距离走动的校正与速度能量的分离与相参积累。 图3 无噪声情况下TRT-KTR算法Fig.3 TRT-KTR algorithm without noise 在回波中添加高斯白噪声,使脉压前信噪比为-18 d B。设平滑处理参考单元数为4,参考门限L为2max(S(tm,fτ))。图4 b)显示,时间翻转相除变换在某些慢时间序号的回波内产生了严重的幅值抬升。由式(19),(20)可知,这是远大于信号值的上突变点引起的。这些海浪式的幅值抬升虽不会掩盖信号能量,但会造成信号能量与回波能量比值降低,干扰信号检测。图4 c)显示,垂直于慢时间维的幅值抬升还会使得Radon变换在搜索角度90°附近产生峰值,严重影响Radon变换搜索速度模糊数。图4 d)显示,经过低通滤波与对超过门限的突变点平滑处理,突变点造成的信号能量抬升被成功消除。采用的线性平滑的方法将突变点去除时会同时去除掉该点的有效信号,损失大约7 d B的信噪比。图4 e)显示,经过突变点抑制后的算法在低信噪比情况下,能够实现动目标速度的分离与相参积累。 图4 有噪声情况下TRT-KTR算法Fig.4 TRT-KTR algorithm in the presence of noise 在实际应用时,可以根据先验信息确定角度搜索范围。假设目标速度范围[-3 000,3 000],则模糊数范围[-200,200],Radon变换搜索角度最小范围为[0,11.309 9]和[168.690 1,180]。这样既规避了在90°附近产生的突变点尖峰,又将计算资源集中在有效区间,同时减少了运算量。 速度模糊数估计精准与否影响距离走动是否能被完全校正,进而影响算法的性能。进行100次蒙特卡罗实验,比较不同信噪比下Radon变换估计速度模糊数的均方根误差(root mean square error,RMSE),仿真结果如图5 a)所示。如果要求RMSE<10-1,平滑后比平滑前性能改善约10 dB。如果要求RMSE<10-2,则平滑后比平滑前性能改善约5 dB。经过低通平滑去除突变点后的模糊数估计RMSE显著小于未去除突变点的均方根误差。 进行100次蒙特卡罗实验,TRT-LTR算法与MTD(moving targets detection)算法检测结果如图5 b)所示。在检测概率要求为0.9时,TRT-KTR算法性能比MTD算法所需信噪比少约7 d B。当要求检测概率为0.95时,输入信噪比至少为-15 d B。本节仿真中,脉冲相参积累个数为400个,积累时间为0.2 s。当脉冲相参积累个数继续增加时,由于MTD没有解决距离走动和距离弯曲问题,回波能量扩散在不同距离单元。TRT-KTR算法相参积累增益更大,性能优势会更加明显。 图5 TRT-KTR算法积累性能Fig.5 Intergration performance of single-target TRT-KTR 假设有3个运动目标做匀加速直线运动,分别为目标A、目标B、目标C。目标A,B,C初始距离分别为10,10,11 km;初始径向速度分别为1 200,-1 600,1 000 m/s;初始径向加速度分别为-500,-500,300 m/s2;积累脉冲数为800。 在无噪声情况下,仿真结果如图6所示。由图6 a)所示脉冲压缩后,3个目标都产生了不同程度的距离走动和距离弯曲。由图6 b)所示,脉压数据在经过TRT-SKT-LVD算法处理后积累出2个尖峰。由于目标A、目标B拥有相同的加速度与初始距离,其能量叠加在一起通过LVD时频处理无法区分两目标。将脉压后目标A,B信号划归一段取出,作TRT相除变换,处理结果如图6 c)所示。由于脉压信号的交叠在时间翻转相除变换后产生了交叉项,交叉项的存在会影响Radon变换搜索模糊数。由文献[12]第2节推导可知,不分段情况下3个目标理论上会产生3个自聚焦项和6个交叉项。通过分段,将A,B划归同一分段,仅产生2个交叉项,减少交叉项数量。图6 d)表明,TRT-KTR算法成功分辨出目标A,B速度。TRT-SKT-LVD和TRT-KTR算法联合可以得到多目标的全部运动参数。 图6 联合算法多目标分辨Fig.6 Joint algorithm for multi-tar get resolution 针对TRT-SKT-LVD算法无法测速的问题,本文提出TRT-KTR算法分离目标回波中的速度分量,采用低通滤波器加线性平滑的方法消除了时间反转相除变换产生的上突变点的影响。对脉压后信号、快时间维分段并行处理,减少了多目标交叉项数量及运算数据量。仿真结果证明,该算法在低信噪比情况下可以有效分离目标速度信息。联合算法可以有效积累出目标距离、速度、加速度三维信息,实现多目标检测。

2 算法原理
2.1 TRT-SKT-LVD算法



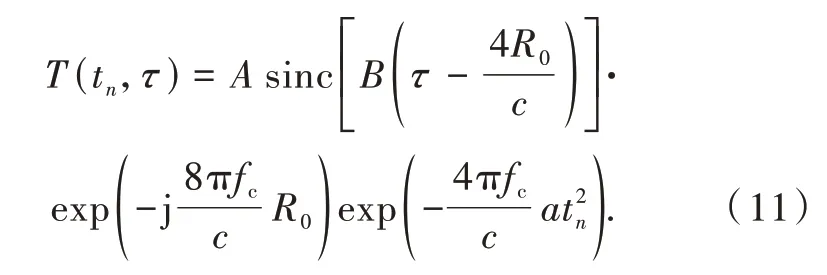


2.2 TRT-KTR算法







2.3 噪声突变点分析
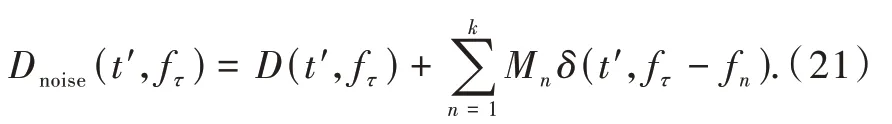

2.4 多目标联合检测分析


3 算法实现及运算量分析
3.1 TRT-KTR算法流程
3.2 运算量分析
4 仿真结果及分析
4.1 无噪声TRT-KTR算法性能


4.2 有噪声TRT-KTR算法性能


4.3 多目标积累性能
5 结束语

