高中数学“一题多解”教学的实践

⦿张家港高级中学 刘 学

1 引言

在高中数学解题教学中，为进一步培养学生的解题技巧与解题水平，教师通常会专门设计一些“一题多解”类的专题训练，鼓励他们面对同一道题目时尽量找出更多不同解法.这一模式能激活学生的自主思维，使其全身心地投入到思考中，有助于他们更好地巩固数学知识与技能.

2 一题多解在教学中的应用

2.1 集合问题的中一题多解

集合是高中数学教材中第一章节的内容，也是高中数学知识体系中的基础构成部分，是学生学习函数知识的前提，虽然题目难度一般，但是也有不少一题多解类试题，教师可以利用这类题目，让学生尝试运用多种方法解决问题，让他们进一步了解集合的含义，体会元素和集合的“属于”关系，为利用集合的思想方法解决简单实际问题做铺垫.

例1已知集合M={x|y2=x+1}，P={x|y2=-2(x-3)}，那么M∩P=( ).

C.[-1，3] D.(-∞，3)

解析：能识别出集合M与P的元素的特征，是求得M和P交集的关键所在.M∩P的元素并非(x，y)，而是x的形式.

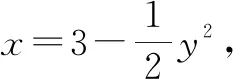
解法2：使用排除法，因为M∩P的元素均是x，并非简单(x，y)的形式，将A排除掉；比较B，C两项，假如取x=-1，-1∈M，-1∈P，得知-1∈(M∩P)，排除B；再比较C与D，取x=-2，-2∉M，D也排除.正确答案为：C.

针对上述案例，学生采用不一样的解题方法处理这一题目，使其理清集合的本质，明确元素的特点具有互异性，再通过代入检验求出两个集合的交集，让他们学会处理该类试题.

2.2 函数问题中的一题多解

函数作为学生从初中阶段就开始接触到的一类知识，步入高中阶段以后，函数的知识范围有所扩大，更是出现不少新型函数，而且对函数的研究更为深入，是学生的学习重点与难点.在高中数学函数解题训练中，教师同样可以利用一题多解类的试题，引领学生从多个角度看待问题，促使他们充分运用所学知识与已知条件通过合理正确的方式来解题.

例2在锐角三角形ABC中，如果sinA=2sinBsinC，那么tanAtanBtanC的最小值是多少？

这是一道典型的三角函数类题目，学生分析、讨论后能够找到以下几种解法.

解法1：根据题意可得

①

令 cosBcosC=tcosA

②

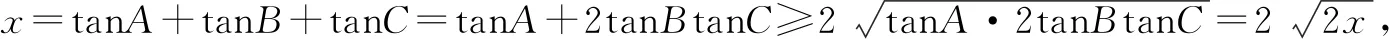
上述案例，从两种完全不同的解题方法来看运用的是两种思路，用到的数学知识也不一样，这样能够拓展学生的思维空间，使其尝试从多个层面与角度解题，让他们学会举一反三.

2.3 数列问题中的一题多解

在高中数学课程教学中，数列也是一类较为重要的内容，包括等差数列与等比数列两大类，在高考中出现的频率较高，是热门考点之一.高中数学教师在数列解题教学中，应当巧妙设置一些一题多解的题目，引导学生灵活运用数列的相关知识展开分析与探讨，有效拓展解题思维空间，使其寻找到最优解题思路与方法，继而提高他们的解题速度与准确度.

例3在等差数列{an}中，a1<0，S9=S12，那么数列{an}的前几项和最小？

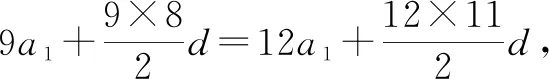
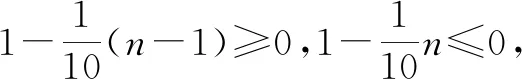
解法2：根据S9=S12可知a10+a11+a12=3a11=0，则a11=0，又因为a1<0，所以公差d>0，据此能够判断出数列{an}前10项或前11项的和最小.

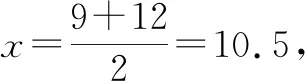
如此，学生分别按照常规思路分析，根据等差数列的概念公式，通过寻找转折项运用等差中项的性质，或采用函数思想将数列问题转化成函数问题的方式解题，使其思路更为灵活.

2.4 不等式问题的一题多解

虽然学生从小学阶段就有所接触不等式，像简单的大于、小于、大于等于、小于等于等算式和数量关系，不过高中阶段的不等式知识更为深奥，涉及到的题目难度也更大，对他们的知识水平与解题能力要求较高.所以，高中数学教师可以在不等式问题中设置一题多解训练，引领学生充分运用所学知识通过多种解题方法来处理问题，增强他们的解题自信心.

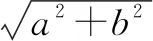
对于上述案例，这三种证明方法跨度大，分别利用基本不等式的性质、复数模的性质及数形结合思想，学生通过寻找更多解题方法，可有效活化他们的数学思维，改善解题水平.

2.5 几何问题中的一题多解

数学主要由代数与几何两大部分构成，高中数学课程体系中的几何知识以立体几何与解析几何为主，对学生的抽象思维能力、几何直观能力与空间想象力有着较高要求，他们在解题中极易遇到障碍.高中数学教师在解题教学环节，可以针对几何问题精心设计一些题目，要求学生运用多种不一样的解题方法，使其掌握更多处理几何问题的技巧，提高解题效率.

A.有两个点PB.有四个点P

C.可能不存在点PD.一定不存在点P

解法1：把线段F1F2当作直径画一个圆，已知圆的半径r=c=3<4=b，所以圆和椭圆不会相交，即不存在点P.

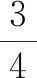
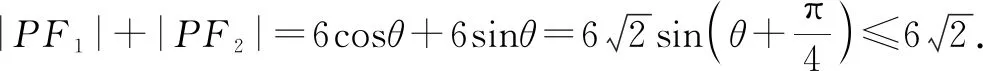
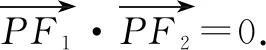
在上述案例中，面对这样一道难度一般的解析几何类题目，学生可以轻松找到多个不一样的解题方法，使其充分体会到一题多解的乐趣，同时让他们通过比较发现最优解题思路.

3 结语

总而言之，高中数学具有较强的理论性与学科性特征，在学习与解题训练中经常会遇到不少挑战，教师应用“一题多解”的训练模式，可以有效活化学生的思维，使其拓展解题思路，掌握高效的解题方法，慢慢增强他们的解题自信.Z