高中数学“边沿”知识数学归纳法的应用
⦿安徽省亳州市蒙城县第二中学 王 浩
1 引言
高中数学课本中有许多重要的数学公式及定理,课本中往往只给出基本形式及其证明,但在很多情况下,我们还会运用它们的推广形式,即需要将它们由特殊形式推广到一般形式.例如指数运算法则,对数运算法则,复数中的棣莫佛定理,二项式定理,等等.但这些定理一般形式的证明往往较抽象、复杂,通常我们只给出其一般形式,很少给出证明.笔者将运用数学归纳法来探究这些常用定理的推广.
2 数学归纳法的应用
2.1 对数运算法则推广的证明
对于对数运算法则,课本中是这样写的:
两个正数的积的对数等于这两个正数对数的和.
若a>0,且a≠1,N1>0,N2>0,
那么 loga(N1N2)=logaN1+logaN2.
此性质可推广为:
loga(N1N2·…·Nn)=logaN1+logaN2+…+logaNn.
即n个正数的积的对数等于这n个正数对数的和.
怎样证明这个推广,当时没有说,现在我们可以用数学归纳法进行严格证明.
证明:(1)当n=2时,等式成立.
(2)假设当n=k(k≥2,k∈N)时,等式成立,即
loga(N1N2·…·Nk)=logaN1+logaN2+…+logaNk,
当n=k+1 时,
loga(N1N2·…·NkNk+1)
=logaN1+logaN2+…+loga(NkNk+1)
=logaN1+logaN2+…+logaNk+logaNk+1,
所以,当n=k+1时,等式也成立.
由(1)(2)可知,对∀n≥2(n∈N*)等式都成立.
2.2 复数棣莫佛定理的证明
关于复数三角形式的乘法与乘方,两个复数相乘,积还是一个复数,模等于各复数的模的积,它的辐角等于各复数辐角的和.
若z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),那么
z1z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].
上面定理也可推广到n个复数相乘的情况,
z1z2…zn=r1r2…rn[cos(θ1+θ2+…+θn)
+isin(θ1+θ2+…+θn)].
这一推广也可以用数学归纳法证明如下:
证明:(1)当n=2时,等式成立.
(2)假设n=k(k≥2,k∈N*)时,等式成立,
当n=k+1时,
z1z2…zkzk+1
=z1z2…zk-1(zkzk+1)
=r1(cosθ1+isinθ1)·r2(cosθ2+isinθ2)·…·rk-1(cosθk-1+isinθk-1)·rkrk+1[cos(θk+θk+1)+isin(θk+θk+1)]
=r1r2…rkrk+1[cos(θ1+θ2+…+θk+θk+1)+isin(θ1+θ2+…+θk+θk+1)],
所以,当n=k+1时,等式也成立.
由(1)(2)可知,对∀n≥2(n∈N*)等式都成立.
特别地,如果r1=r2=…=rn=r,θ1=θ2=…=θn=θ时,就有
zn=[r(cosθ+isinθ)]n=rn(cosnθ+isinnθ).
这就是复数乘方公式,通常称作棣莫佛定理.
2.3 均值不等式推广的证明
在不等式中,已经学习了均值不等式,即两个正数的算术平均数不小于它们的几何平均数,它们的几何平均数又不小于它们的调和平均数.
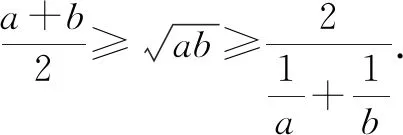
将上式推广,对于n个正数也有相应的平均数的概念及关系.
如果a1,a2,…,an是n个正数,那么
证明:下面先用数学归纳法证明
①
不妨设0 当a1=an即a1=a2=…=an时,上式成立; 当a1 (1)当n=1时,不等式成立; (2)假设n=k时不等式成立,即 又因为 所以 当n=k+1时, 两边都乘k+1次方,应用二项式定理,可得 这就是说 所以 由(1)(2)可知,对∀n∈N*式①都成立. 上述证明还说明了当且仅当a1=a2=…=an时,①式中等号才成立. 下面再证: ② 证明:因为a1,a2,…,an都是正数,由①式得: 所以 综合①②式就证得原不等式. 通过知识的拓展,提升学生逻辑思维及推理能力,数学归纳法作为演绎推理的一种,培养学生逻辑地思考问题,在比较复杂的情境中把握事物之间的关联,让学生感受数学推理的严谨和理性精神,也让学生体会数学推理与证明的独特魅力.Z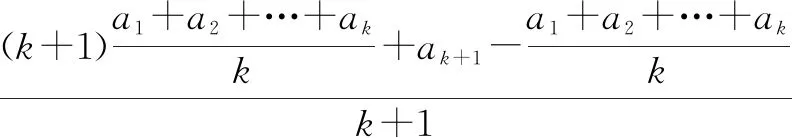
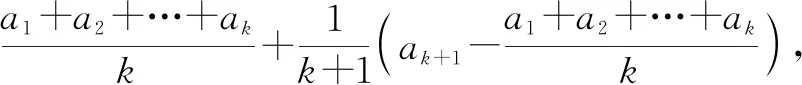
3 结束语

