化繁为简勤探求，抽丝剥茧触本质*

⦿福建省莆田第一中学 林 敏

1 引言

圆锥曲线问题常在压轴题的位置出现，是学习的一大难点.由于其运算的复杂性与转化的灵活性常使考生望而却步，而且问题的转化程度和所要面临的运算通常成反比，即转化程度越低，需要进行的计算就越复杂.所以在解圆锥曲线的相关问题时，不能盲目地进行低效的转化从而踏入繁杂的运算中后“一根筋”地“硬算”，而是在开始进行运算之前，更应当仔细审视条件和结论之间的关联，探求其内在本质，注重高效转化，精简计算，避免运算的繁复程度，真正实现圆锥曲线内容考查的价值和意义.

下面以新高考圆锥曲线压轴题为例进行研究，通过不断修正解法，以期达到精简的水平.

2 试题背景

(Ⅰ)求C的方程；

3 问题解决

3.1 试题分析

首先，本题的整体设问以双曲线为背景，是之前在旧高考中很少出现的情形.以往一般在小题中考查双曲线有关的内容，多以离心率为依托，涉及双曲线的性质和相关的代数运算，而这道题的出现打破了大题只考椭圆或抛物线的壁垒，让人眼前一亮.

其次，本题的设问条件是线段之积相等，以往一般只涉及一条相关弦长的表示与计算，该题涉及到四条弦长，让人顿感计算量飙升，但仔细思考又觉得别有洞天.

虽然题目的设置有很多创新之处，但该题依然保持着高考命题的稳定性.第一问考查较为常规的根据定义求圆锥曲线标准方程的问题，轨迹方程问题向来是备考中练习得比较充分的题型，学生完成起来没有压力，只是此题需要稍微注意下变量的范围；第二问虽然看似是在求值，但实际上是一种圆锥曲线定值问题的证明，根据条件证明斜率之和为定值，也不会让学生感到陌生，所以是在继承传统的基础上加入了创新元素，做到了新旧高考的完美转换与衔接，逐步体现学生的学科素养水平.

3.2 解题探索

3.2.1 问题初解

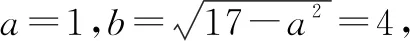
初看此题，虽觉运算可能较多，但不至于无从下手，可以从最常规的思维路径中寻找到出路，我们来看一下常规思路对应的解决方法.

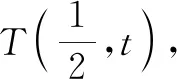
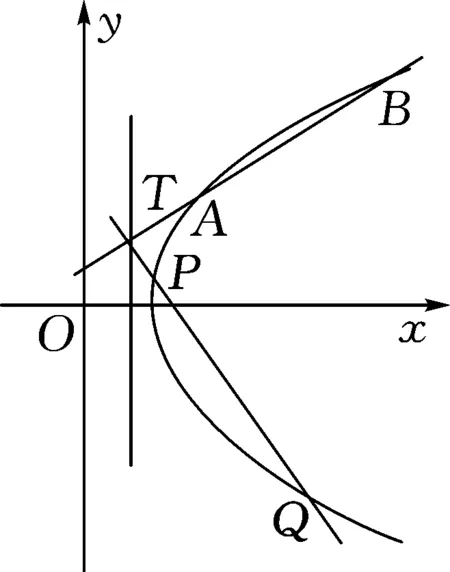
图1

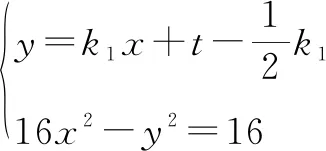
设点A(x1,y1)、B(x2,y2)，则x1≥1，且x2≥1.

在该方程判别式为正的情况下由韦达定理可得

因此，直线AB与直线PQ的斜率之和为0.

3.2.2 解后反思

该常规解法把直线的斜率作为主要的运算变量，点T的纵坐标为辅助运算变量(最终结果与之无关)，利用弦长公式实现了已知条件的表达.在联立消y的过程之中，若没有将直线的纵截距看成一个整体进行运算的话，得到的方程的形式将会更加繁杂而且写出韦达定理、代入计算也是比较复杂的过程，运算量较大，容易出现一定的错误，并不是那么容易就得出形式简洁的结果，所以思维含量较低时就需要借助于较为复杂的计算实现问题的解决.在该解法中，若不选用弦长公式，可以选用向量的坐标运算来进行表达：

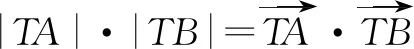
从而得到和上面一样的结果.

3.3 解法优化

3.3.1 优化思路

当我们用上面的解法完成这个题的求解之后，总会有意犹未尽的感受，所以不应该就此结束对这道题的思考.如果能够让这个题的解答更漂亮些，就需要我们回头反思在解题过程中可以优化的地方，不断地增加思维的探求深度，这样也更容易触及问题的本质，通过增大思维上的含量，来降低运算的复杂度.所以有时我们不应只停留在解决一个题的层面上，更要探求如何有效地解决，以及辐射与之相关的问题.

3.3.2 初步优化

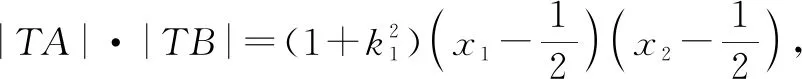
3.3.3 二次优化

由于T点既不在x轴上也不在y轴上，所以直线的方程较为繁杂，与曲线C联立后就更显复杂.基于简化坐标从而简化直线方程的视角，从这个突破口出发，可以考虑将图形整体平移，使得T所在的直线与y轴重合，虽然曲线C的方程稍有变化，但是整体运算还是会较为简洁的.

图2

因此，直线AB与直线PQ的斜率之和为0.

此时就和一道简单的圆锥曲线问题无异了，在不断的优化过程中找到了更为简洁的方法，增加了思维含量，大大降低了运算的难度和容量，降低了出错的可能；而从方程类型的角度，也可以继续进行优化.

3.3.4 三次优化

前面我们从代数形式和图形位置的角度对解法进行了优化.除此以外，若不改变图形的整体位置，则可以考虑方程属性的改变，即普通方程较为繁杂的时候可以考虑选用参数方程，而且由线段之积相等非常容易让人联想到利用直线的参数方程，由参数的几何意义表达线段长度的积，借助于三角恒等变换获得直线AB和PQ倾斜角之间的关系，从而得到斜率之间的关联.

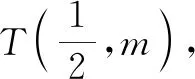
点评：该优化方法充分考虑了题目给出的条件特征，将复杂的线段长之积利用参数方程化为参数的积，建立等量关系，得到直线倾斜角的互补关系，进而得到了斜率之和为0的结论，宛若神来之笔.在新教材中，坐标系与参数方程的相关内容已经被删去了，但是在旧高考模式下选做题之一还是重点考查的，而在本题中使用参数方程的方法能起到较好的效果，体现了新高考的兼容并包和对旧高考的致敬，新旧交替的过程中实现完美的过渡，体现了教育有改革，育人不间断的特点，所以该题是一道比较有韵味的问题，而解决该题更是一种对美的追求和享受.

4 总结