解决一类函数与导数压轴题的基本策略
——以2021年浙江省高考压轴题解析为例
⦿杭州第七中学 刘富裕
1 引言
2021年浙江省压轴题表述简洁,立意新颖,知识交汇丰富,多层次多角度地考查了学生的数学思维和素养[1].该题将函数、导数、函数的零点与不等式知识结合,考查学生灵活运用导数工具分析和解决问题的能力,对逻辑推理、数学运算、直观想象等核心素养要求较高,为高校选拔和学生进一步学习所需掌握的技能、思想、方法创造条件[2].
2 原题
设a,b为实数,且a>1,函数f(x)=ax-bx+e2(x∈R).
(1)求函数f(x)的单调区间;
(2)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围;

3 题目剖析
第(1)小题比较常规,主要考查函数单调性的问题,这里要注意的是对参数的讨论;第(2)小题涉及到函数零点求参数范围,也是浙江高考连续两年都涉及到的问题;第(3)小题属于双变量含参不等式的问题,这也是近几年高考的热点问题的.解题思路如图1:
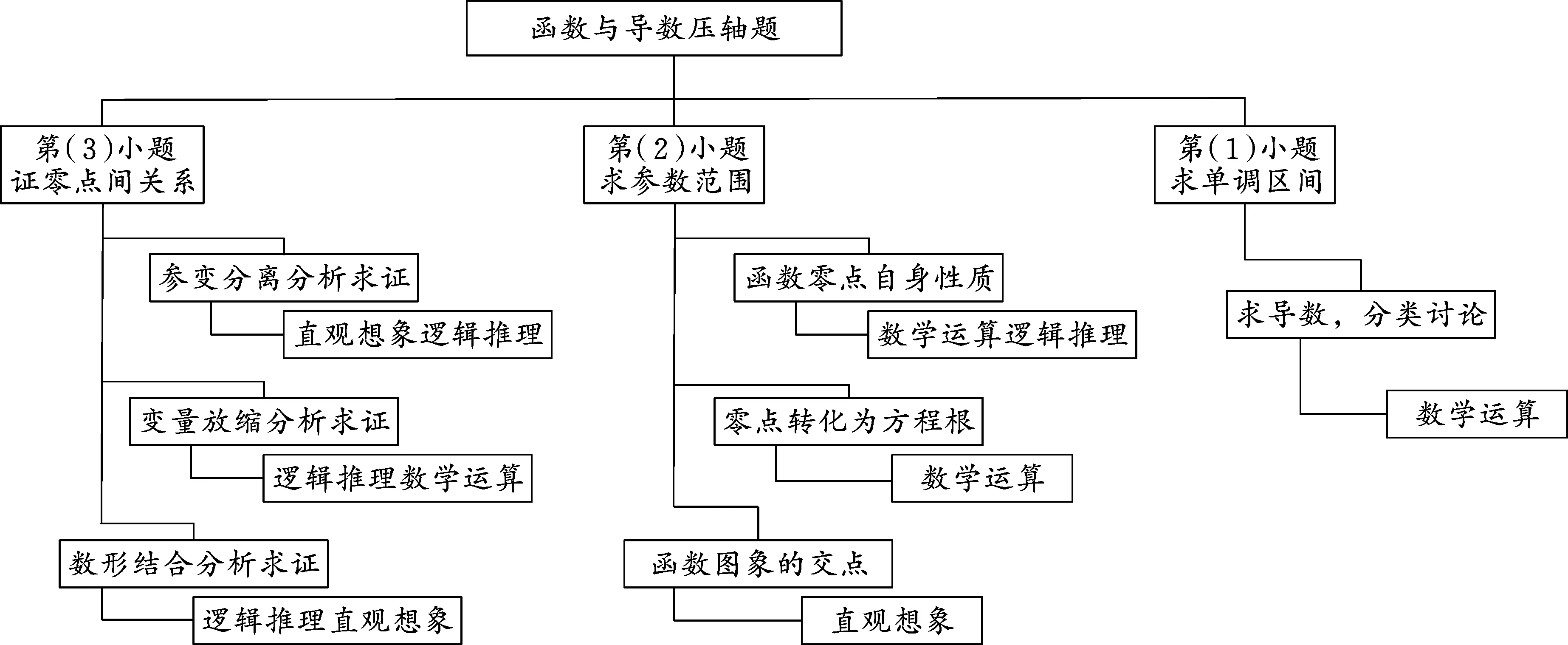
图1
4 解法探析
4.1 第(1)小题解法探究(直接求导,正负定界)
由于f(x)=ax-bx+e2(x∈R),所以f′(x)=axlna-b.
①若b≤0,则f′(x)=axlna-b>0,所以f(x)在R上单调递增;
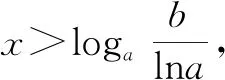
这种利用导函数来判断函数单调性是比较常规的题目,本小题要注意的是对参数b的讨论,这里的难点是对指数函数的求导以及极值点的表示.
4.2 第(2)小题解法探究
回归到原点,本小题主要涉及到知识点为函数零点.对于函数零点的问题,可以从函数零点自身性质、对应方程的根以及函数图象的交点这三个方面去切入,找到解题突破口.
4.2.1 极限叙述、进阶放缩
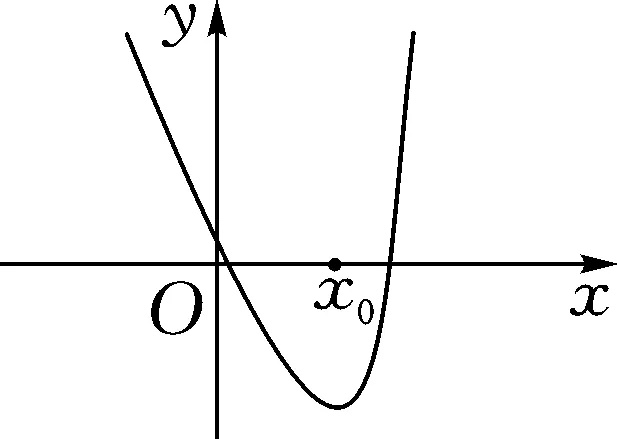
图2

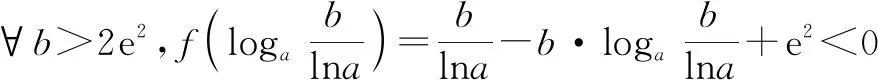
使用换底公式再去分母化简为:
⟺[1+ln(lna)]b-blnb+e2lna<0.
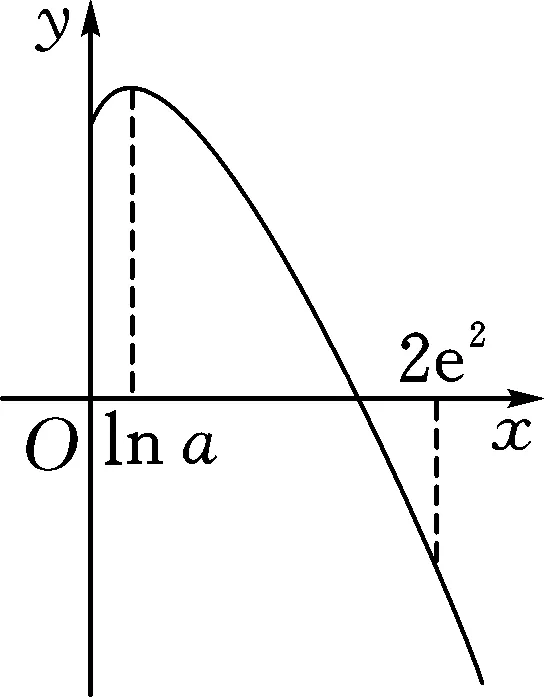
图3
记上述不等式左侧为g(b),则其导函数为g′(b)=ln(lna)-lnb,b>2e2.
易知g(b)在(0,lna)单调递增,在(lna,+∞)单调递减.
又因为gmax(b)=g(lna)=lna+e2lna>0,所以结合函数图象(如图3)可知:
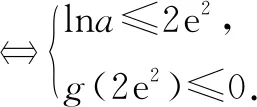
由g(2e2)=e2[2ln(lna)+lna-2ln2-2]≤0,可得2ln(lna)+lna-2ln2-2≤0,即2ln(lna)+lna≤2ln2+2.
又因为函数y=2lnx+x在x∈(0,+∞)上单调递增,结合lna≤2e2,0 这种方法是从零点自身性质出发,结合函数单调性,把“函数有两个零点”转化为“恒成立问题”,进而求参数的取值范围.过程中涉及到构造函数,并把b看作变量,体现了双参主元的思想[3]. 上述方法运算量比较大,我们还可以对其进一步改进与优化. 赫利森的研究描述了同一通道的免疫功能。它们提供了一种方法,让更多第一反应的白细胞比来自腿骨骨髓的白细胞更容易受到急性脑损伤。这一结果叫板了目前的观点,认为骨髓损伤后均匀释放白细胞进入血液循环,从而到达炎症部位。 则g(x)在x∈(0,1]上单调递增,在x∈(1,+∞)上单调递减. 以上过程,首先是从函数零点出发,然后使用极限叙述、进阶放缩的方法,最后通过恒成立问题求出参数的取值范围[4].在此过程中,也涉及到换元、构造函数、数形结合等方法,主要考查了学生的数学运算、直观想象、逻辑推理等核心素养. 4.2.2 换元转化,构造函数 记h(t)=et(t-1)-e2,则 h′(t)=et(t-1)+et·1=et·t>0. 又h(2)=0,所以t∈(0,2)时,h(t)<0,t∈(2,+∞)时,h(t)>0. 则g(t)在(0,2)上单调递减,在(2,+∞)上单调递增. 因此lna≤2,即1 此方法把函数零点转化成对应方程的根,从方程根这个角度切入,然后通过换元、二次构造函数,利用函数单调性求参数范围.过程中涉及到等价转换、二次构造、二次求导等方法,对学生的数学运算、逻辑推理的核心素养有较高的要求.但考场上时间有限,我们需要一种简化运算的方法.接下来,我们尝试从函数图象入手. 4.2.3 分参思想,利用切点 函数f(x)有两个零点,等价于函数f(x)与x轴有两个交点,但与x轴交点无法求得. 设h(x)=ax,g(x)=bx-e2,则转化为两函数图象有两个不同的交点. 设切点坐标P(x0,y0),画出函数图象(图4). 图4 发现当b为定值时,随着a的变化,两函数图象交点个数是不确定;而当a为定值时,无论b如何变化,函数图象始终有两个零点.所以,对于∀b>2e2,两函数有两个交点时,当且仅当g(x0)>y0. 从而ax0lnax0-e2=ax0.令t=ax0,则tlnt-e2=t,切点坐标为P(logae2,e2). 由g(logae2)=blogae2-e2>e2,b>2e2,得logae2≥1,从而1 这种方法是从函数图象切入,把函数零点问题转化为两函数有两个交点.从两函数相切逆推到函数图象相交的情况,从而求出参数a的取值范围. 总体上看,第(2)小题主要是双参数求参数取值范围的问题,我们首先从数学原点和题目原点出发,分别利用零点存在性质得到不等关系、利用函数最值性质得到不等关系、利用切点性质得到不等关系,最后求出参数的取值范围.在此过程中主要考查学生的逻辑推理、数学运算、直观想象等核心素养. 第(3)小题是不等式的证明,可以从原点出发,挖掘已知条件,类比第(2)小题的做法去切入;也可以从要证明的结论切入,对其变形、等价、或简化等. 4.3.1 参变分离,分析求证 从参数b入手. a=e时,f(x)=ex-bx+e2有2个不同零点x1,x2(x1 由于ex+e2=bx,则x>0.结合函数图象(图5),知f(2)=e2-2b+e2<0,则x1<2 图5 因为f(x1)=f(x2)=0, 又因为b>e4,所以bln(lnb)>e4ln4>e2显然成立.证毕. 首先把函数零点转化为对应方程的根,分离参数b,利用数形结合求出x1的取值范围,进而使用放缩法和分析法证明了结论.这里的f(2)<0是很难想得到的,我们采用数形结合的方法去处理,主要考查学生直观想象能力. 4.3.2 变量分离,分析求证 结合第(2)问可知,当a=e且b>e4时,f(x)恒有两个不同的零点. 由于f(2)=2(e2-b)<0,可得x1<2; 由于f(x1)=ax1-bx1+e2=0,得bx1=ax1+e2,所以,对待证不等式右侧替换和放大: 此方法把函数零点转化成对应方程的根,和解法1不同的是此方法分离的是bx1,进而对要证的不等式放大,最后用分析法求得结果.主要考查学生的逻辑推理、数学运算等核心素养,同时也要求学生对放缩法和分析法掌握得比较熟练. 以上两种方法分别是从参数b和变量x1,x2考虑,方法很巧妙,但运算量非常大.类比第(2)小题,我们用数形结合来简化运算,此题也可以尝试去从函数图象这个角度切入. 4.3.3 数形结合,分析求证 图6 由a=e,f(x)=ex-bx+e2,∀b>e4知x0=lnb,故f(x)恒有两个零点x1,x2(x1 f(0)=1+e2>0,f(1)=e+e2-b 由0=f(x1)=ex1-bx1+e2,得bx1=ex1+e2 只需证(e2-e)lnb>2. 而b>e4,知(e2-e)lnb>4(e2-e)>2成立. 从函数图象切入,利用函数图象估计x1的范围,再用代数的方法去验证,然后用放缩、分析法求证.体现了数形结合的思想,这个过程中主要考查了学生直观想象的核心素养. 纵观第(3)小题,主要是考查双变量含参不等式化为含参数的零点问题,这里的变量又是函数零点,所以将函数零点与对应方程的根互相转化,进而用分析法求证. 本题是函数与导数的压轴题,对于此类题目,我们需要“回归原点”.这里的“原点”,一方面是指试题涉及的“数学的原点”,即概念、定义、公式、定理、基本知识和思想;另一方面是指给出的“试题的原点”,包括涉及的题型、结构,数据、条件,变形、推论等.以后遇到此类问题时,我们可以从方程、不等式、切线、最值、极值等等切入,最后落脚点都是函数[5].坚定函数思想、明确函数意识是求解这类问题的基本.解题过程有如下感悟: 导数大题运算繁,双参函数定主元; 复杂算式需变换,先猜后证变简单. 这也充分考查了学生逻辑推理、数学运算、直观想象等核心素养,同时对学生的创新能力的要求也越来越高[6].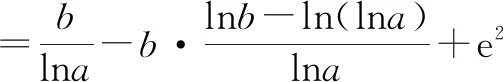
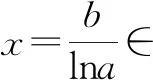


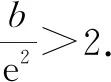
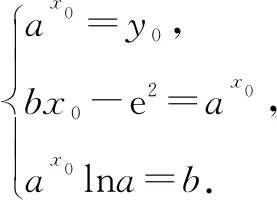
4.3 第(3)小题解法探究
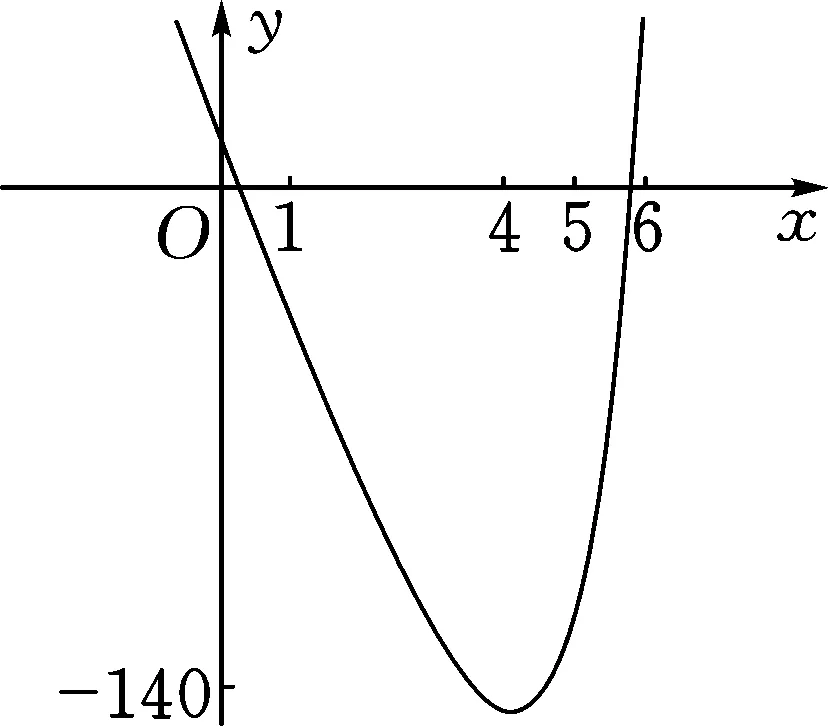
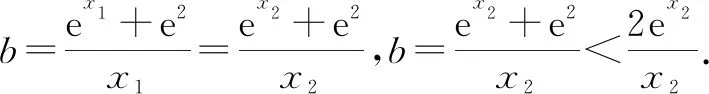
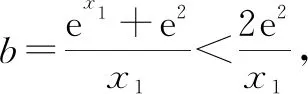
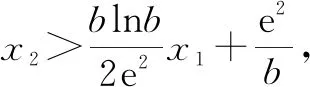
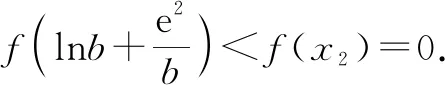


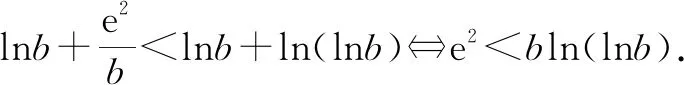


5 反思总结

