一道三角函数求值题的多角度分析

⦿湖北省十堰市房县第一中学 陈清先

1 引言

三角函数值的求解是近年高考数学中的一个热点问题，此类问题往往情境创设简单新颖，设置方式变化多端形式各样，难度适中．此类问题的特点就是背景设置多变，三角公式众多，切入点多样，破解方法多种，对各层次学生能力的考查都有一定的体现，可以很好地考查学生的数学运算与逻辑推理能力，充分体现高考的选拔性与区分度．

2 问题呈现

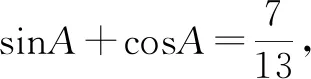
此题条件简捷，短小精悍，难度适中，以三角形的内角的取值范围来确定对应角的取值限制，通过相关角的正弦值和余弦值的和式来创设题目条件，在此背景下求解相应角的正切值问题．此题主要借助情境创设，结合题目条件，综合考查同角三角函数基本关系式，三角形的基本性质等基础知识，同时综合考查化归与转化的数学思想方法，以及数学运算、逻辑推理等核心素养．

3 问题破解

思维视角一：三角函数思维

方法1：方程法.

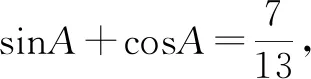
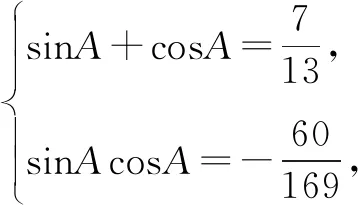
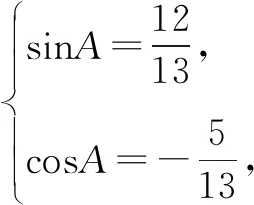
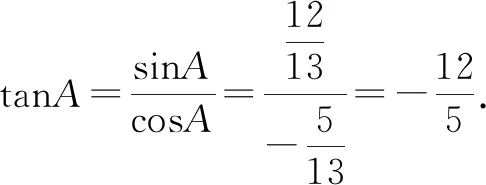
故选择答案：A．

点评:结合条件中同角三角函数的正弦值和余弦值的和式进行两边平方处理，结合平方关系的变形与转化，得到对应积式的值，并结合条件确定角A的取值限制，利用联立方程组求解相应的角的正弦值和余弦值，利用商数关系来确定对应角的正切值．方程思维是破解同角三角函数问题中比较常见的思维方式，注意点就是把握角的取值范围的限制对三角函数值的影响．

方法2：同构法.

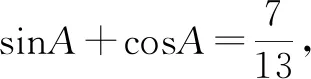
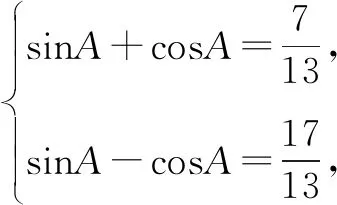
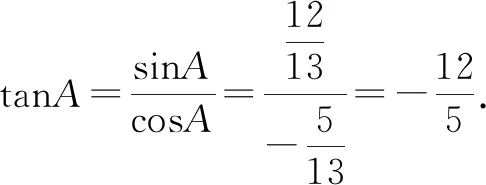
点评:结合条件中同角三角函数的正弦值和余弦值的和式进行两边平方处理，结合平方关系的变形与转化，得到对应积式的值，并结合条件确定角A的取值限制，结合同角三角函数的正弦值和余弦值的差式的平方的求解，通过联立方程组求解相应的角的正弦值和余弦值，利用商的关系来确定对应角的正切值．合理同构，利用同角三角函数的正弦值和余弦值的和式与差式互为对偶式，在进行求值与运算时经常通过同构来确定目的．

方法3：齐次化法.

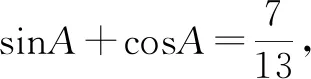
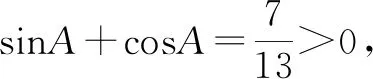
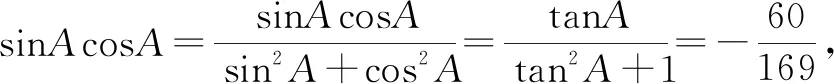
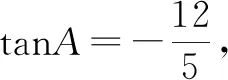
故选择答案：A．

点评:结合条件中同角三角函数的正弦值和余弦值的和式进行两边平方处理，结合平方关系的变形与转化，得到对应积式的值，并结合条件确定角A的取值限制，通过对应积式的齐次化处理，转化为涉及tanA的二次方程，结合方程的求解与条件的限制来确定对应角的正切值．齐次化处理，将问题转化为所要求解的三角函数值的方程问题，通过方程的求解与条件的限制来分析与处理．

思维视角二：解析几何思维

方法4：数形直观法.

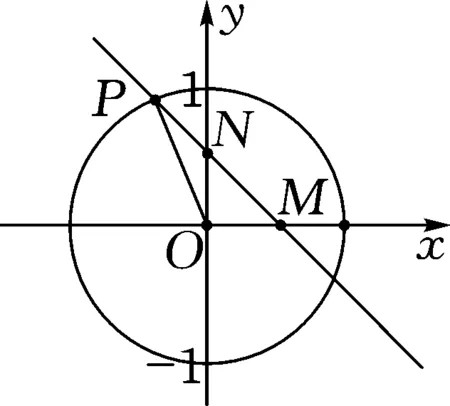
图1

解析：如图1所示，建立平面直角坐标系Oxy，设P(cosA，sinA)，其中∠A=∠POM.

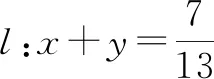
而A为三角形的内角，则点P在第二象限内.

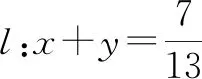
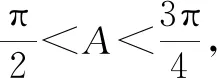
故选择答案：A．

点评:通过建立平面直角坐标系，结合三角函数的定义，将三角函数问题转化为直线与圆的交点问题，利用平面几何与解析几何的性质确定角A的取值范围，利用正切函数的单调性来确定tanA的取值范围，结合各选项中的值直接得以分析与判断．数形直观法是在平面直角坐标系的背景中，结合直线与圆的位置关系，数形结合，通过解析几何思维的直观转化来实现．

方法5：解三角形法.

解析：如图1所示，建立平面直角坐标系xOy，设P(cosA，sinA)，其中∠A=∠POM.

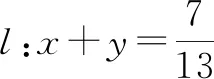
而A为三角形的内角，则知点P在第二象限内.

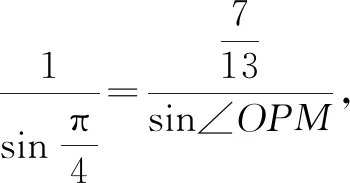
故选择答案：A．点评:通过建立平面直角坐标系，结合三角函数的定义，将三角函数问题转化为直线与圆的交点问题，通过平面几何知识的直观分析，确定对应角与边的大小，通过正弦定理的过渡与转化，结合同角三角函数基本关系式、三角恒等变换公式的应用来确定对应角的正切值．解三角形法可以将三角函数问题平面几何化，综合平面几何、解三角形、三角函数等相关知识来综合与应用．

4 教学启示

4.1 熟记基本公式，掌握通技通法

借助三角函数知识来处理此类问题，破解的关键就是熟练掌握三角函数中的基本公式，涉及同角三角函数基本关系式、诱导公式、三角恒等变换公式等．在具体破解时，结合题目条件对三角函数式进行切化弦、化同名、化同角等常规处理，掌握基本的通技通法，巧妙转化，灵活应用．

4.2 回归定义本源，拓展思维方式

建立在三角函数定义基础上的三角函数问题，往往可以借助三角函数定义的回归，结合定义本源，通过平面几何、平面解析几何等相关知识来构建，从而在平面几何、平面解析几何等知识基础上进行拓展与延伸，或数形结合，或坐标转化，借助图形特征或代数运算来处理，实现思维方式的拓展与提升．Z