高中数学分层教学“五分四列”法

⦿安徽省颍上县第一中学 穆 勇

1 引言

分层次教学的理论依据是“因材施教”的原则[1]，现实依据是人的个体差异.由于每个学生的学习基础、兴趣爱好、智力水平、学习潜力、学习动机、学习方法、学习态度等存在差异，比如笔者所在的一所普通高中，学生从高一入学时就存在着明显的差别(因为学校根据入学成绩将他们分编为重点班、普通班)，而且在每个不同类型的平行班内，学生对数学的学习兴趣和爱好程度又不同，对数学知识的接受能力也有明显的差异.如果我们忽视这些现实存在的差异，仍然沿用同一种教学方法来进行教学，不仅违背了“因材施教”的教学原则，也很难收到预期的教学效果.所以在实际教学中，既要面向全体学生，考虑到学生的共性，更要照顾到他们的个体差异，针对不同的学生层次，因材施教，采用不同的教学方法，这样才有可能全面提高教学质量.“五分四列”法是笔者在高一数学分层次教学活动中的一些探索和尝试，与大家分享.

2 学生分层列比例

开学初，笔者对授课的2个平行班其中一个班的65名学生进行了一次数学测试，结合他们的入学成绩、爱好、兴趣、特长及性格特征，按照教学大纲中对“基本目标、中层目标、发展目标”这三个层次的教学要求，将学生按照2∶5∶3的比例分为A，B，C三个层次.其中A层(13人)属于学习成绩较差的学困生，他们中的大部分同学能够听懂课堂内容，能较好地完成课堂练习及部分简单的课外习题；B层(32人)属于相对平稳的中等生，他们中的绝大多数能够在听懂、理解课堂内容的基础上，独立完成作业或习题；C层(20人)属于成绩优秀的优生，他们不但能够听懂、理解课堂内容，能够自觉、独立完成课内外各种作业，还能够自觉预习，并主动地辅导帮助B层、A层的学生，与A层学生结成帮扶学习小组.

如何分层，分层是否恰当合理，关系到“分层教学”的成功与否，所以在具体分层的过程中，要贯彻“慎重、磋商、动态、调整”的原则.首先，教师要给学生讲清分层方案设计的目的、意义和方法，以消除学生的思想顾虑和抵触情绪，特别是要向学习基础差的学生表明，分层并不是抛弃他们、不管他们，而是为了更好地帮助他们提高学习成绩；其次，要引导学生客观公正地评估自己，在自我评估的基础上，让学生自己先选择适合自己的层次，教师再做适当的调整；最后，教师对每个层次的学生实行动态管理，根据期中、期末的考试成绩灵活作及时调整.

3 目标分层列要求

针对不同层次的学生，可列出不同层次的教学目标：A组学生达到“识记、领会、简单应用”的初级目标；B组学生达到“识记、领会、简单应用、简单的综合应用”的中级目标；C组学生达到“识记、领会、简单应用、简单的综合应用、较复杂的综合应用”的高级目标.例如，在讲授必修2第3章第2节“直线的点斜式方程”时，就对三个不同层次的学生提出了以下不同的要求：A组的学生能够理解直线方程的点斜式、斜截式的形式特点和适用范围，能正确利用直线的点斜式、斜截式公式求直线方程；B组的学生在准确理解直线方程点斜式、斜截式各种特征的基础上，能够熟练运用公式求解直线方程；C组学生能够熟练解答关于直线点斜式方程、斜截式方程的各类应用题，探究直线的斜截式方程与一次函数的关系.

4 教学分层列计划

4.1 循序渐进

三个层次的学生中，B层“中等生”的人数最多，是班级的主体，他们中勤奋一点的学生，经过努力能够很快挤进C层“优生”的行列，但如果一松劲，也会滑进A层“学困生”的队伍，因此，加强对“中等生”的管理和教学至关重要.所以，制定教学目标和计划时可以以“中等生”为参照，按照“循序渐进、分层对待”“抓中间促两头”的原则[2].对“优生”列出的目标和计划，要高一些、长远一些，让他们时时处于一种“跳一跳，摘到更大桃子”的不满足状态中；教师千万不能认为，反正这些优生成绩稳定，学习很自觉，用不着老师操心，让他们靠天赋吃饭，而又吃不饱饭，长此以往，既浪费了智力资源，又失去去了分层的意义.对“中等生”和“学困生”列出的目标和计划，要充分体现“实用性”“激励性”和“可行性”，如果给他们定的目标太高，难以实现，可望而不可即，会让他们失去自信；如果目标太低则失去了激励性，同样失去了意义.所以，对“中等生”和“学困生”的教学不能急于求成，要通过对他们每次的考试成绩详细分析(优势、劣势、发展潜力等)后，在此基础上分层次、分阶段、分人制定并适时调整具体的目标和计划.

4.2 避免分化

对靠近“优生”的学生要时刻关注、关心他们，督促他们严格要求自己，勤学好问，不断激发他们的进取心和赶超意识，充分发挥出他们应有的水平，推动他们向“优生”靠拢和转化.对靠近“学困生”的学生更不能忽视，因为他们一旦放松要求，很有可能失去自信，滑进“学困生”的行列；对这部分学生，教师要及时发现、抓住他们的优点和细微进步，多给予表扬、鼓励，并与家长、班主任、其他科任教师沟通、配合，督促其按时完成学习任务，养成自觉、良好的学习习惯，发掘他们的内在潜力，逐渐引导他们自觉学习，主动向“优生”层级靠拢，防止扩大“学困生”队伍.

4.3 共同提高

实行分层教学的最终目的就是为了共同提高.要充分发挥好“优生”的表率和带头作用，让“优生”与“学困生”结成帮扶学习小组，让“优生”利用课余时间给“学困生”和“中等生”补习、个别辅导，及时消化和巩固知识.这样做，既能使“中等生”感到受重视，激发内心深处的自尊、自强、进取意识而努力拼搏，又能让“优生”得到展现才华的机会，发现自身的价值，还能让“学困生”受到触动和鞭策，感受到一种强有力的刺激，看到希望，增强学习的信心.

5 作业分层列顺序

在学完一个章节的内容后，学生要通过及时做练习来巩固和提高.教师布置作业时也要分层次，要根据不同层次学生的学习能力，布置不同类型的作业，列出A，B，C先后顺序，体现出台阶式梯度.一般可分为三个层次：A层是基础性作业(以课堂练习为主)，B层以基础性作业为主，同时配有少量略有提高的题目(课外习题)，C层是基础性作业再加有一定灵活、综合性的题目(课外拓展类复习题)各半.要把握好作业的难易度和完成时间，一般学生在20至30分钟内完成.例如在“直线的点斜式方程”一节的教学中，给学生布置了如下三个层次的作业供他们选择.

第一层：1.确定一条直线的几何要素有哪些？

2.若直线l的倾斜角为α(α≠90°)，则直线的斜率k=.

3.已知直线上两点P1(x1,y1),P2(x2,y2)(x1≠x2)，则直线P1P2的斜率为.

4.两条直线平行与垂直的判定：对于两条不重合的直线l1,l2，其斜率分别为k1,k2，有l1∥l2⟺，l1⊥l2⟺.

5.直线l经过点P0(-2,3)，且倾斜角α=45°，求直线l的点斜式方程，并画出直线l.

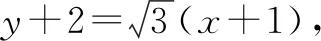
2.已知点A(7,-4),B(-5,6),求线段AB的垂直平分线的方程.

3.分别写出下列直线的点斜式方程：

(1)经过点A(2,5)，斜率是4；

(2)经过点B(-2,-1)，与x轴平行；

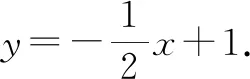
(1)求过点(2，3)且垂直于l的直线方程；

(2)求过点(2，3)且平行于l的直线方程.

2.已知直线l的斜率为k，且l与y轴的交点为(0,b)，求直线l的方程.

3.已知直线l1:y=k1x+b1,l2:y=k2x+b2,试讨论：

(1)l1∥l2的条件是什么？

(2)l1⊥l2的条件是什么？

既然学生的层次不同，教学目标和要求不同，当然各个层次学生的各类作业(数量、难易程度)也就不同，只有这样布置作业才能真正起到“训练、巩固、提高”的作用，也能减少学生抄作业、应付差事等现象.

6 分组帮学促提高

为适应新课改“合作、探究”的需要，把全班65名学生细分为13个学习小组，每组5人，其中每组1名A组的“学困生”，3～4名B组的“中等生”，1～2名C组的“优生”，这样“好、中、差”搭配编组，主要是为了帮扶“中、差”层级的学生.组内指定1名“中等生”轮流担任“发言人”或“组长”，由他负责把本组预习、探究、讨论的意见、问题或结果整理汇总，向全班或科任老师提出来；为了“促后进”，组内指定一名“优生”一对一帮扶1名“学困生”，随时解答他们学习中的困惑和疑难，帮助他们树立学习数学的信心，不断提高学习成绩.例如班上有一位李同学，高一开学初数学测验的成绩只有45分，基础差，上课听不懂也不专心听讲，课后抄作业，考试作弊，晚上在宿舍里玩手机上网.但经过“优生”王同学半学期一对一的耐心辅导帮扶，学习态度有了明显的转变，考试成绩也逐次提高，到期末考试时已经提高到65分，第二学期期末考试时成绩达到了78分，由原来的A组流动到了B组.经过一年的教改实验，全班的数学单科平均成绩有了显著的提高.

实践证明，面对全班学生“参差不齐”的实际情况，分层教学“五分四列”法不失为一种有效的尝试，它能够促使学生更加明确学习目标，增强学习的自觉性，激发学习兴趣，明显地缩小“优”“差”两极分化[3]，逐渐提高班级数学的整体水平.