海上风力机多场平台构建及地震动力学研究

闫阳天， 李 春,2， 缪维跑， 岳敏楠， 牛凯伦

(1. 上海理工大学 能源与动力工程学院， 上海 200093；2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)

针对海上风力机遭受地震及多种环境载荷作用的结构安全问题，美国和欧洲海上风电发展较为迅速的国家和地区已制定了相关规范。挪威船级社(DNV)、丹麦Risφ国家实验室、德国劳氏船级社(GL)[1]、美国风能协会(AWEA)[2]及美国土木工程协会(ASCE)[3]分别针对各国特有的气候、地质地理条件制定了相关设计规范。规范中主要涉及3个方向：计算方法、结构模型及风-震-波浪场耦合模型。

海上风力机会遭受不同大小的湍流风、波浪及海流载荷。针对环境载荷多变的海上风力机，国内外诸多学者采用不同的耦合模型对风力机正常运行时遭受突发性地震冲击下的结构响应展开研究。

早期学者们基于建筑规范中常用的地震响应谱分析法计算风力机地震响应[4-5]。Ma等[6]对比了瞬态分析法与响应谱分析法计算所得地震作用下的塔架结构响应，发现响应谱分析结果较瞬态分析结果更剧烈，按照建筑规范程序设计风力机基础会导致对地震载荷评估过于保守。Witcher[7]认为针对传统建筑地震评估采用的频域法不能解决地震载荷与气动载荷同时作用的气弹问题。Santangelo等[8]认为响应谱分析法在解决气弹和土壤柔性这2个关键问题上存在缺陷。杨阳等[9-10]基于FAST软件建立湍流风-地震时域耦合模型，模拟风力机在不同土质和地震强度下的塔架动力学响应。上述研究基于FAST构建了考虑气动载荷、波浪载荷及土-构耦合(SSI)效应的多体动力学耦合模型，且运算准确高效，但计算结果比较宏观，针对结构局部承载规律研究能力薄弱。有限元方法可以有效弥补这一不足。若采用有限元壳模型进行研究，基于计算流体动力学-计算结构动力学(CFD-CSD)的全耦合时域方法计算昂贵且低效。Santangelo等[8]采用非耦合时域法降低计算消耗量，研究了5 MW风力机在地震及风载荷作用下的结构响应，发现与全耦合仿真结果相比，时域非耦合分析亦可得到较为准确的结果。

风、浪载荷通常是海上风力机结构设计中最重要的环境载荷，因此在研究风力机结构地震响应时有必要考虑[11]。目前的研究方法主要依赖海上风力机的准静态载荷计算[8]。Sun等[12]研究风力机在风、波和地震载荷下结构响应和振动控制，其中对于风载荷，采用叶素动量理论计算作用在旋转叶片上的气动载荷，固定桩基承受的波浪载荷采用莫里森方程计算。李颖等[13]基于FAST探讨了研究地震响应时考虑风、浪载荷的必要性。Wang等[14]研究了风、浪、流和地震联合作用下的结构响应，结果表明土-构耦合效应及多种环境载荷缺一不可。但在研究海上风力机地震动力学时，针对是否考虑环境载荷的必要性探讨尚显不足。

针对上述问题，笔者以10 MW单桩海上风力机为对象，采用有限元方法构建海上风力机非线性Winkler土-结构耦合模型，并在此基础上建立了复杂的土-桩-塔架非线性壳模型。通过对模态计算结果的校核，确保构建有限元模型的有效性，并基于上述模型进行从局部到整体的瞬态分析，研究其在风-浪-海流载荷作用下的地震动力学响应，为大型海上风力机结构设计和优化提供参考。

1 研究对象

2012年，丹麦科技大学(DTU)与丹麦Vestas合作设计了一款10 MW及以上容量风力机[15-16]。笔者以DTU 10 MW风力机为研究对象，假设风力机安装海域平均水深20 m；埋土桩基38 m，根据不同土壤性质将其分为非等长的6段；塔架壁厚随塔高线性减小；塔基外径为7 665 mm，壁厚为34 mm；塔顶外径为5 500 mm，壁厚为26 mm。塔架选用密度为7 850 kg/m3、弹性模量为210 GPa、泊松比为0.3、材料屈服极限为380 MPa的A709圆截面高强钢。考虑到结构油漆、法兰、螺栓和焊接质量，计算密度修正为8 500 kg/m3。

1.1 有限元方法及模型

在求解瞬态问题时，采用有限差分法，通过对动力作用和反应过程的时间离散来求解瞬态问题。对于具有线性阻尼和刚度的单自由度系统，控制弹簧-阻尼-质量系统运动的动力学方程为：

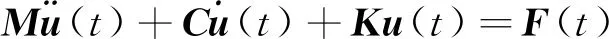
(1)

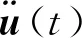
解决结构系统动力学响应的最常用方法是动力平衡方程的直接数值积分方法。求解微分方程的方法较多，从这些方法获得的解被假定为具有连续高阶导数的光滑函数，但是非线性结构的精确解要求加速度和位移的二阶导数不是光滑函数。因此，针对加速度不连续性的求解，Newmark开发了一系列单步积分方法，用于解决爆炸和地震载荷下的结构动力学问题，称为Newmark时间积分方法。

对风力机的支撑结构建立3D有限元模型。采用壳单元模型，并针对连接位置局部网格进行细化，具体支撑结构的有限元模型如图1所示。

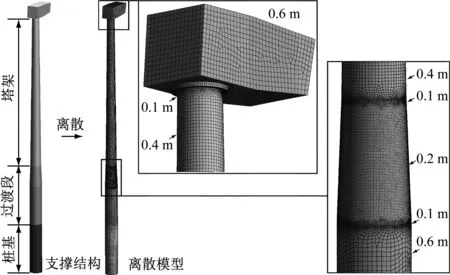
图1 支撑结构及有限元模型

1.2 土-构耦合模型

建立土-构耦合模型时，结合p-y曲线法与Winkler土-结构耦合模型[17]，采用非线性弹簧描述埋土桩基与土壤间的相互作用，基于p-y(土壤反力-横向位移)曲线及Q-z(土壤反力-纵向位移)曲线确定横向、纵向的非线性弹簧刚度。土壤参数如表1所示，其中E为弹性模量，γ为有效土重度，fc为单位表面压力，ft为表面拉力，q为桩底单位阻力。

景观娱乐用水区，指以满足景观、疗养、度假和娱乐需要为目的的江河湖泊等水域。景观娱乐活动不得危及景观娱乐用水区的水质控制目标。

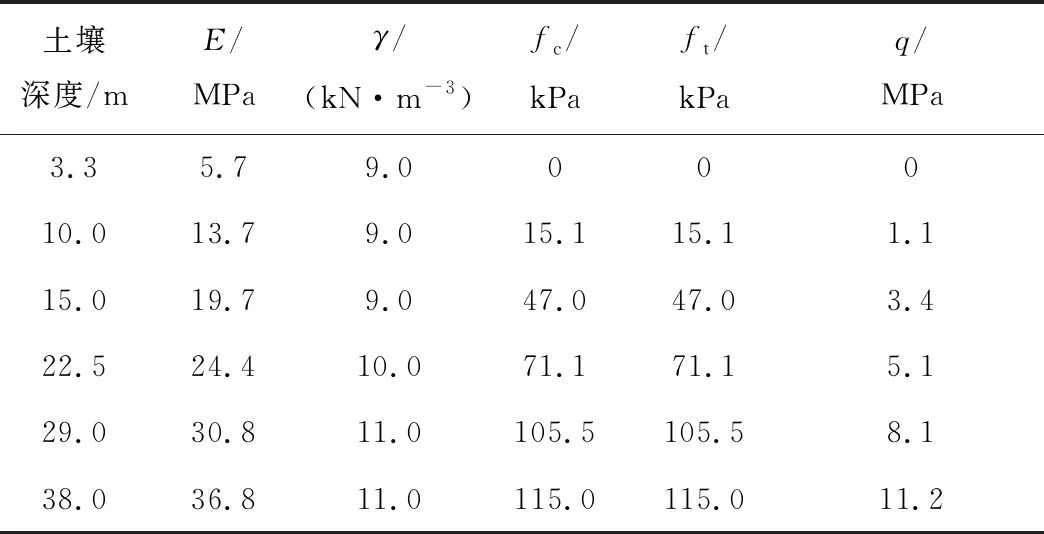
表1 土壤参数

p-y曲线是非线性的，并且沿单桩深度(H)变化。API规范中根据最终的横向承载力pu来得到p-y关系，这取决于该深度的土壤属于浅层土还是深层土，深浅的划分由桩基外径及土壤力学性质共同决定。砂性土的p-y曲线表达式为：

式中：A为经验调整系数，A=3.0-0.8H/D；y为横向位移；m；pu为桩深至H时的极限承载力，kN/m；pus为浅层土时的极限承载力，kN/m;pud为深层土时的极限承载力，kN/m；k为地基反力系数，kN/m3；D为桩基外径，m；C1、C2与C3为系数，由内摩擦角φ确定[17]，分别取3.2、3.6和60。

经计算，不同土壤深度处的p-y曲线如图2所示。

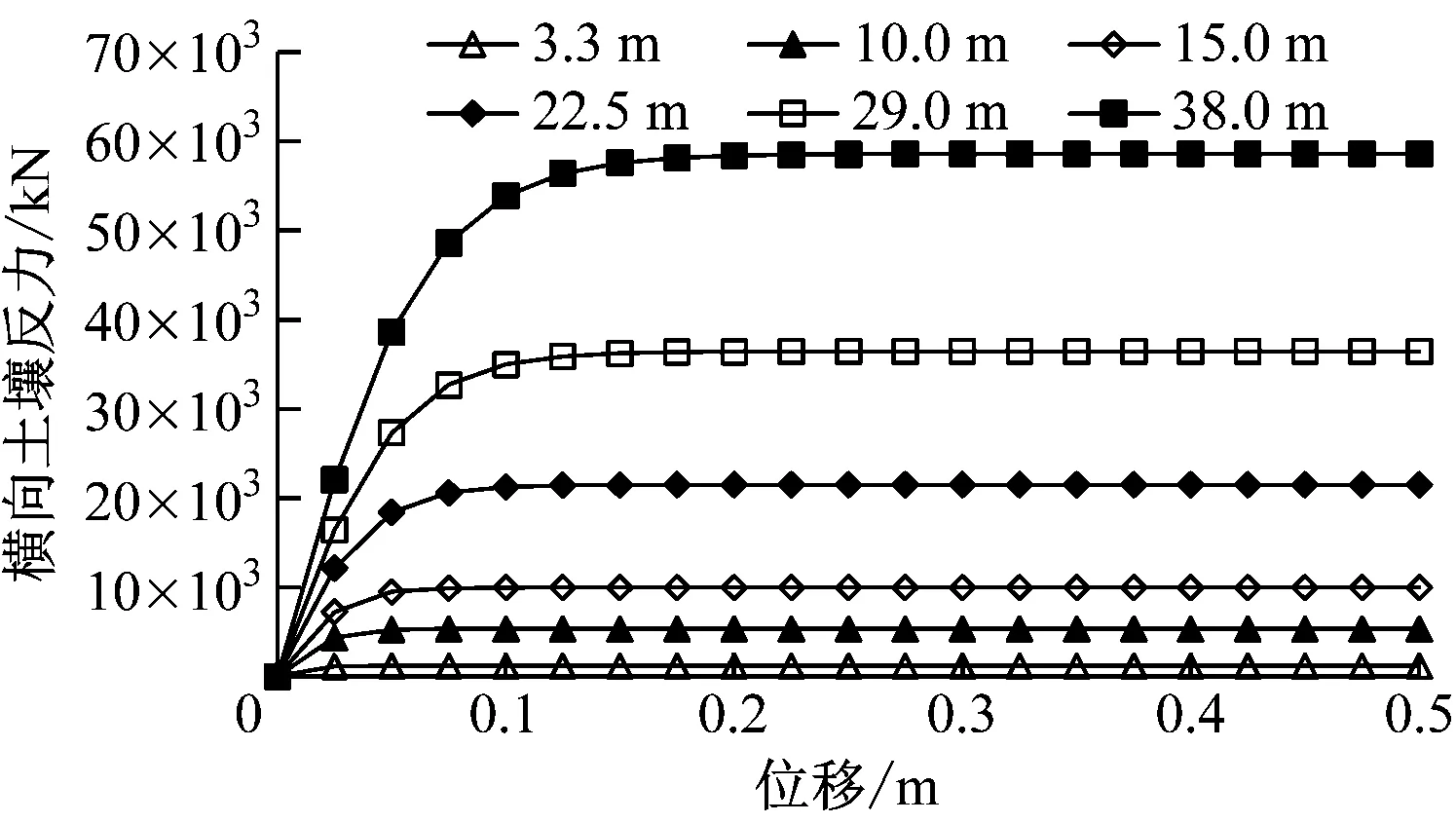
图2 不同土壤深度处的p-y曲线

2 多场耦合模型构建

笔者构建了考虑湍流风、波浪、海流及地震的多场非全耦合模型，见图3，其中K1～K7为非线性弹簧刚度。将250 m×236 m的湍流风风场通过以轮毂为中心的13×13个节点进行计算，每根叶片由37个质点的多体模型描述，气动载荷采用FAST中的AeroDyn求解。波浪和海流载荷通过在AQWA中定义P-M谱进行求解。地震载荷将实测地表位移响应作用于非线性土-构耦合模型，地震携带能量通过土-构耦合模型传至桩基。

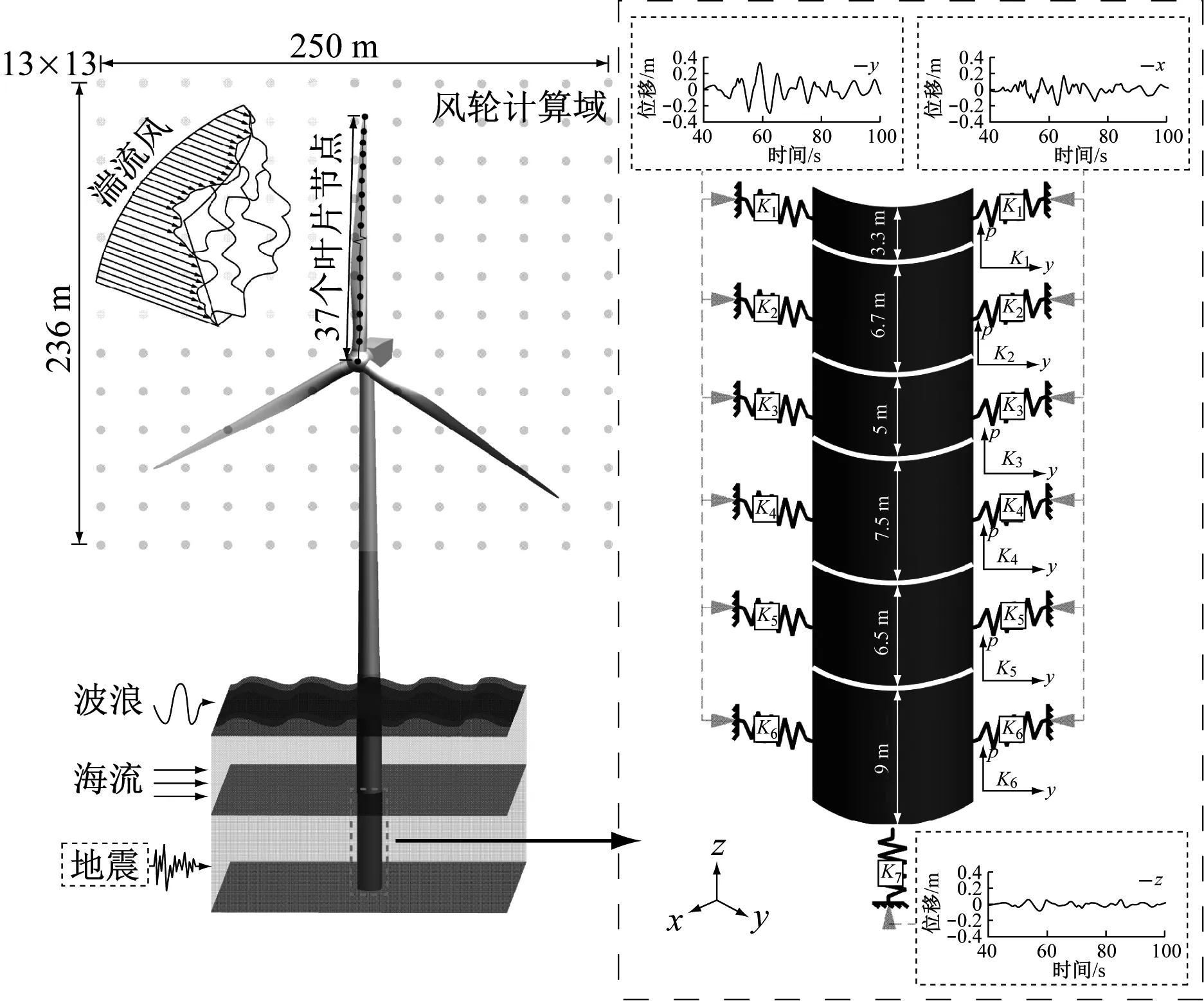
图3 多场耦合模型

2.1 湍流风

建立湍流风风场模型的关键是选取合适的风谱模型，笔者采用IEC Kaimal风谱模型，湍流风载荷的计算结果如图4所示，可以看出因变桨效应导致切出风速时结构承受的风载荷更低。

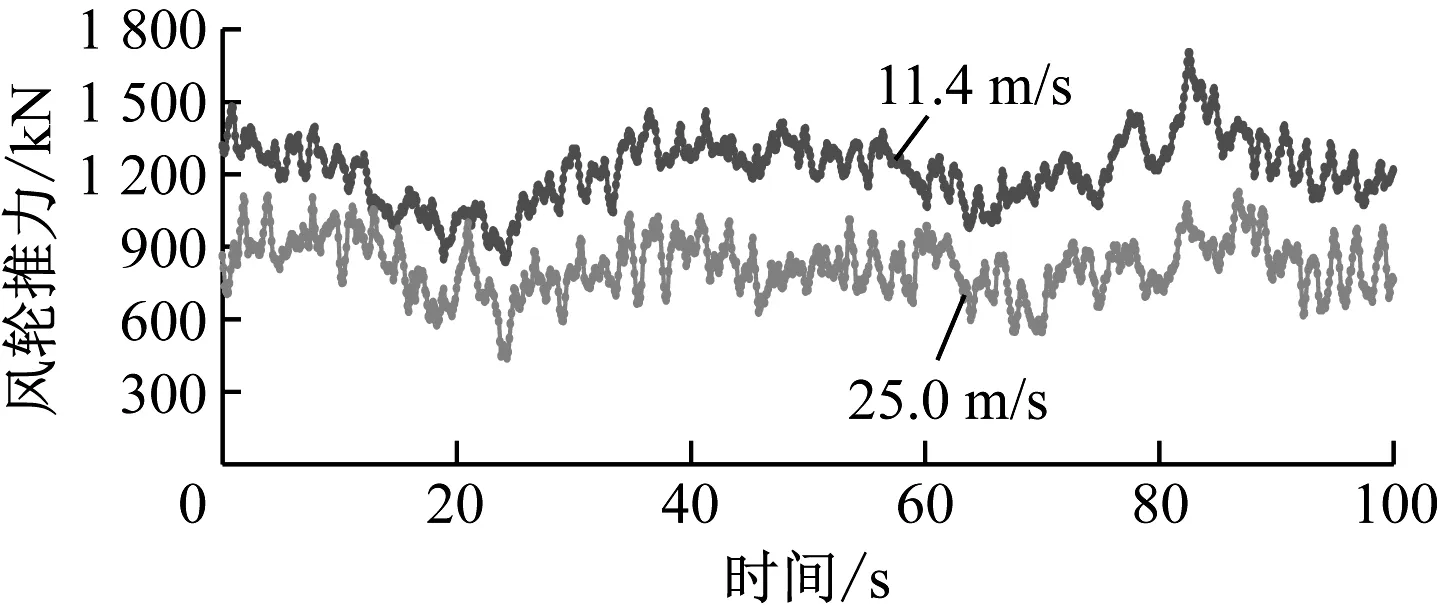
图4 湍流风载荷时域图

2.2 波浪与海流

使用Morison方程可以有效计算出振荡流中作用在圆柱体上的力。该方程将单位长度的总力描述为阻力和惯性力的总和：

(6)

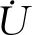
2.3 地震运动

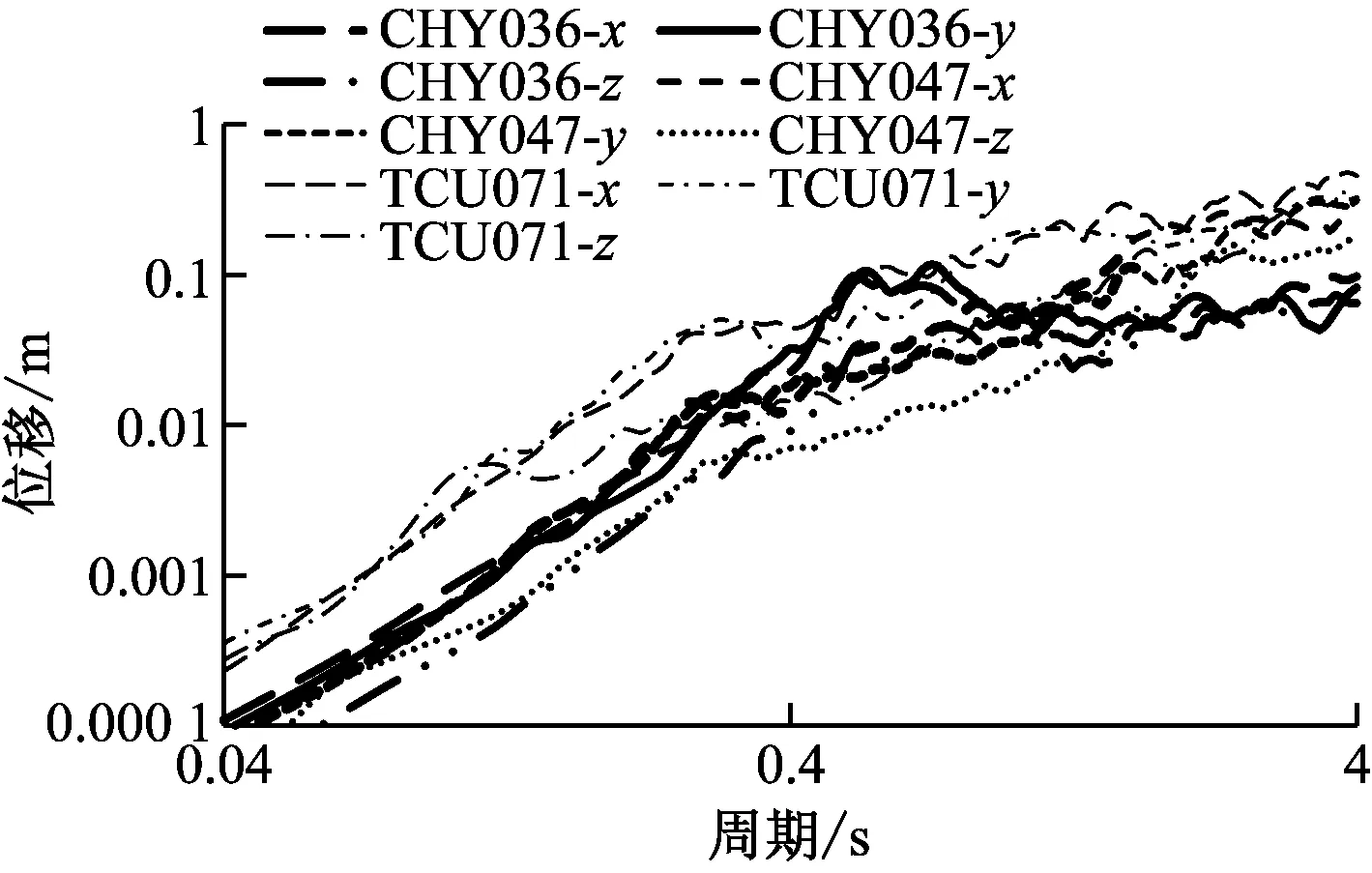
图5 各地震载荷x、y和z方向位移谱

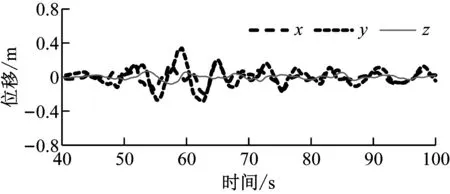
(a) 监测站CHY036

3 结论与分析

为更准确地研究地震响应时湍流风、波浪及海流载荷同时作用对结构的影响，针对不同地震发生时湍流风、波浪及海流载荷的作用构建13个工况，计算载荷如表2所示，考虑波浪载荷的工况时，海流载荷固定为4 m/s。总计算时长为100 s，载荷步为0.02 s，根据瞬态交变载荷增量的不同，将各载荷步划分子步，每个算例计算步长不超过15 000步，每个算例计算时长约28 h。

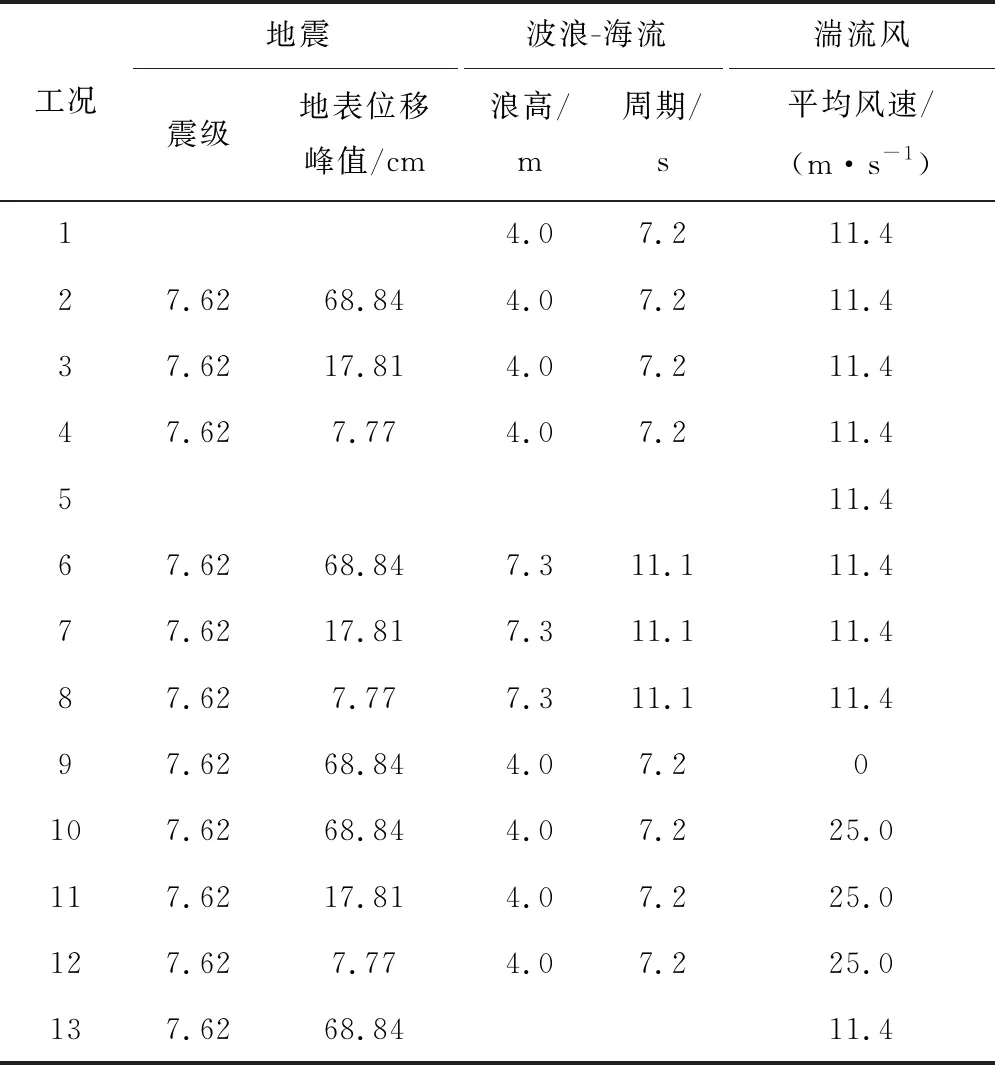
表2 计算载荷

分析各种环境载荷变化对地震动力学响应的影响。在时域内给出了整个风力发电系统的塔顶位移和应力应变能。为了研究不同高度时沿塔身周向的应力分布，按照图7所示定义周向探针分布，设置湍流风来流方向为0°探针，每间隔30°布置一个探针。

图7 塔架周向应力探针分布

3.1 地震载荷

针对变地震载荷条件下结构塔顶位移、结构应力及应变能进行时域响应分析，结果如图8所示。

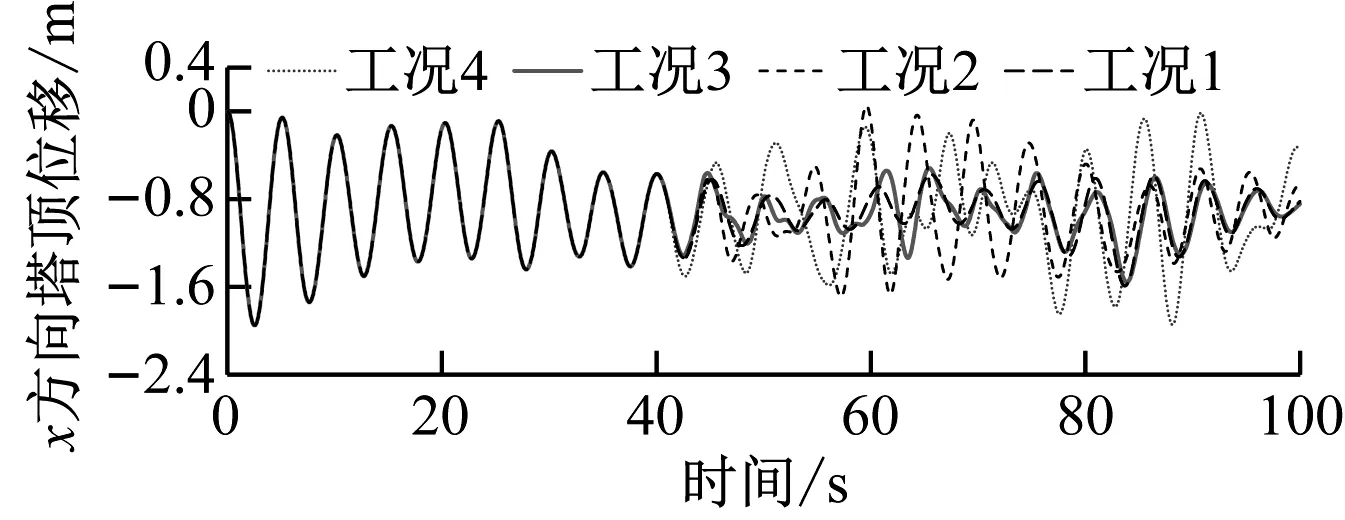
(a)

从图8可以看出，工况1～工况4为4种变地震载荷工况，地震均发生自风力机启动运行后的第40 s，各对比算例的时域响应在前40 s保持一致，由无地震发生的工况1可知，风力机启动的前20 s各响应波动幅度较大，随后随湍流风风速的变化而变化，但整体趋于平稳。随着地震的发生，结构各时域响应产生不同程度的增幅，塔顶位移变化更为显著。由图8(a)～图8(c)可知，塔顶在x方向发生偏心往复运动，风、浪载荷造成塔顶位移在y和z方向位移分量远小于地震载荷。风、浪载荷虽然方向与大小不稳定，但主要以来流方向为主。而地震载荷各方向分量大小由横波、纵波的大小决定，无主流方向。x和y方向的位移增幅明显大于z方向，说明结构横向遭受地震载荷冲击对地震载荷更敏感。工况2～工况4选取的地震PGD依次降低，但工况4所受应变能与应力峰值最大，工况2其次。结合图6发现，产生这一现象的原因是与工况2相比，工况4的PGD数值较小，但持续时间长，且近地位移响应在x和y方向分量较大。工况4的位移峰值出现在80～90 s，原因是在该时刻结构因风、浪载荷导致局部响应峰值，因此在风力机结构地震研究时，需重视横波导致的结构横向响应，且需要同时考虑风、浪载荷。

对工况 2～工况 4地震发生后结构应力达到峰值时的表面应力依据图7的思路进行提取，结果见图9，工况后面给出的是应力峰值时间。应力响应达到峰值时支撑结构壁面应力在塔高方向的分布均呈现自上而下的非线性递增现象。湍流风来流方向为0°，即探针Path0的位置。因此，此刻应力峰值出现在Path0与Path6，即0°与180°附近。由图9(a)可以看出，该现象是由强劲的湍流风载荷导致的，随着地震载荷的加入，以工况4为例，由图9(d)可知应力最大区域在周向上分布的最大位置在0°～50°及200°～250°，峰值区域向逆时针方向转动。

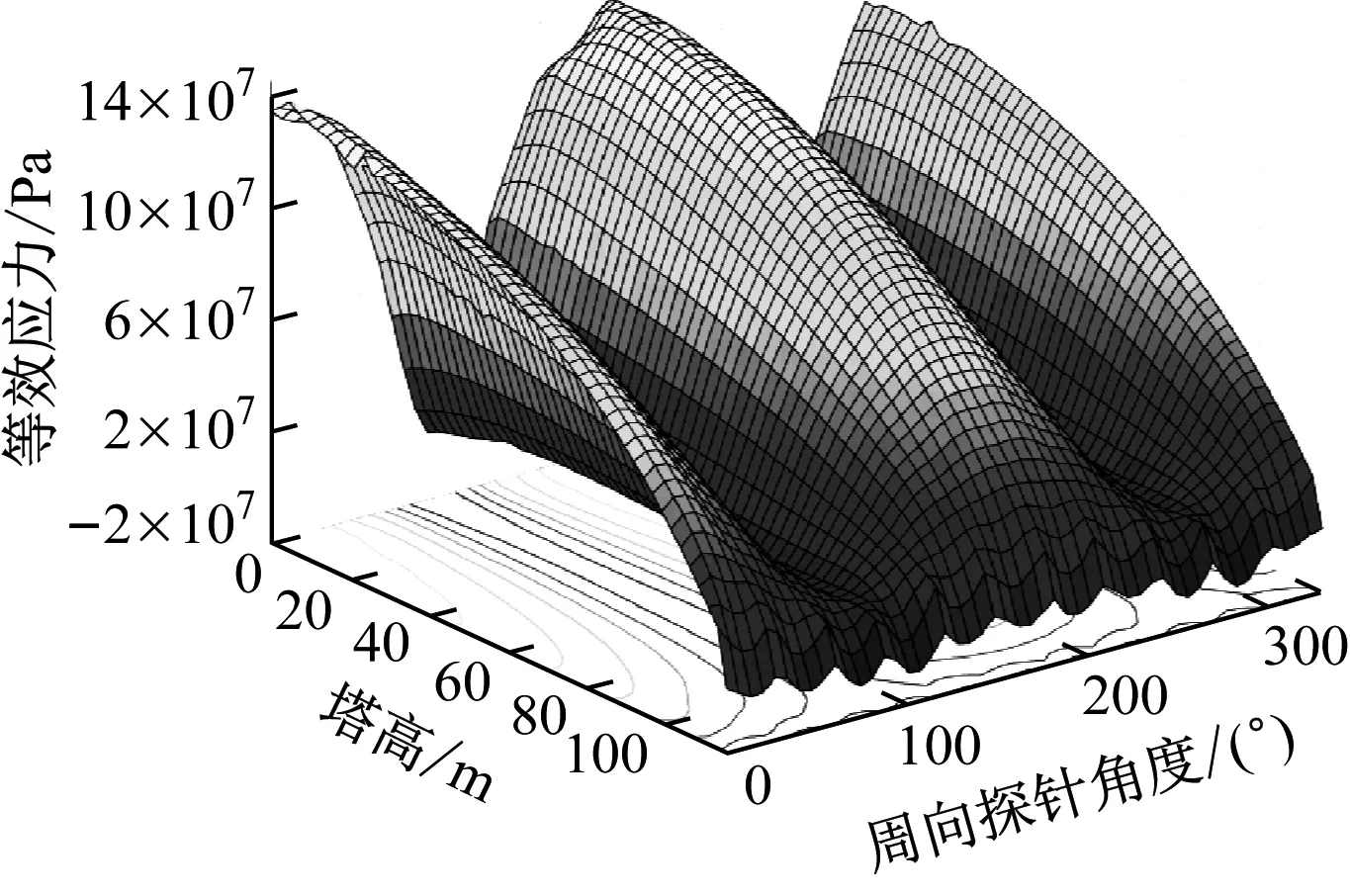
(a) 工况1-83.62 s

图10为变地震载荷条件下峰值时刻塔架位移云图，其中最左边的图是未发生地震载荷时的位移云图。图11为变地震载荷条件下峰值时刻应变能云图。

图11 变地震载荷塔架应变能云图

结合峰值瞬间支撑结构的位移及应变能进行分析。风力机在遭受湍流风及地震作用时，结构产生的响应以一阶模态为主，主要为塔顶的前后及横向位移。应变能集中在26 m左右塔高位置。从图10可以看出，风力机启动造成的塔顶位移幅值高于地震及湍流风所造成的位移响应幅值。湍流风作用对结构塔顶运动起主导作用，地震造成塔架底部应变能的聚集，对比工况 1与工况 4发现，地震造成的塔架位移及应变能增幅相较于风、浪造成的结构位移及应变能增幅较小，所以在地震发生时控制风、浪载荷可实现减少地震威胁结构安全的可能。

图10 变地震载荷塔架位移云图

3.2 湍流风载荷

依据位移、应力及应变能的时域和瞬间响应，分析变湍流风载荷工况的影响。

图12为相同地震载荷及波浪载荷作用下，3种变湍流风载荷工况的结构时域响应，所选取的工况 2、工况 9和工况 10分别为额定风速(11.4 m/s)、无风载荷及切出风速(25.0 m/s)作用下支撑结构时域响应。从图12可以看出，0～40 s时，因采用变桨系统，额定风速下结构时域响应幅值最高，说明结构承受的风载荷也更剧烈。当地震发生后，使得结构动力学响应瞬间急剧增加，但三者风载荷的不同导致各响应增幅差异较大。工况9比另外2个工况的响应波动频率更高。根据上述现象发现，地震载荷造成的结构响应频率较风载荷更高，额定风速下结构承受风载荷更强，反而与地震载荷同时作用产生的结构动力学响应更小，说明湍流风载荷产生了气弹阻尼效应，导致结构受地震冲击产生的响应幅值增加，加速了地震传递至结构的能量耗散。

(a)

图13给出了变湍流风载荷时的周向应力分布。可以看出，工况 2、工况 9和工况 10下的应力响应分布规律基本一致，结构应力产生峰值的时间较为接近，因此支撑结构应力达到峰值的时间主要取决于地震载荷。工况10应力幅值明显大于工况2和工况9，而工况9与工况2的应力幅值较为接近。高风速下，结构承受湍流风载荷较小，低风速下反之。但地震发生时，高的风载荷起到的气弹阻尼效应可有效降低结构应力的激增，基于此可开展有效的结构抗震设计。

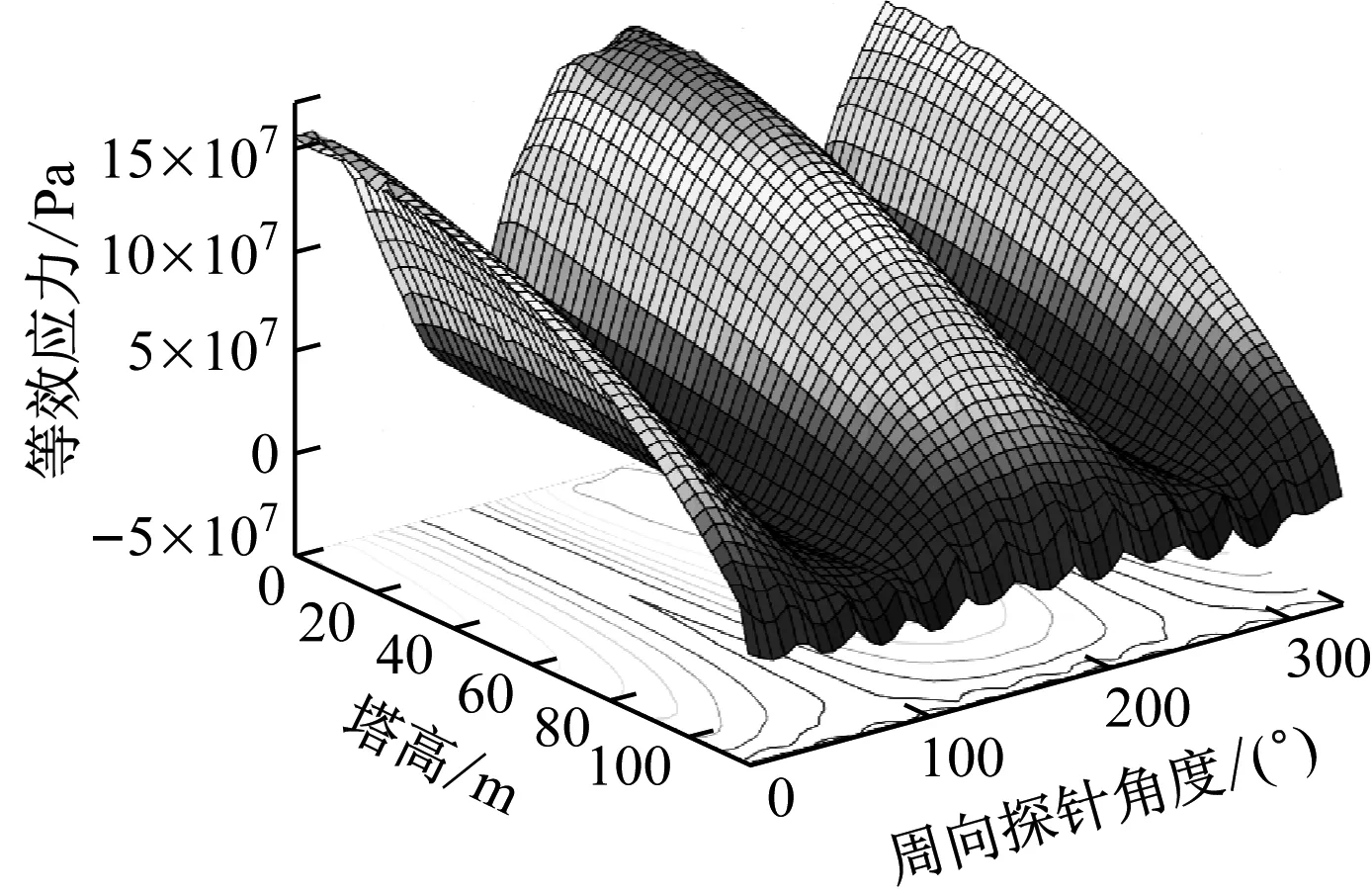
(a) 工况2-61.60 s

图14给出了变湍流风载荷条件下峰值时刻塔架位移云图，其中左边的3个图是未发生地震载荷时的位移云图。图15给出了变湍流风载荷条件下峰值时刻应变能云图。

图14 变湍流风载荷塔架位移云图

对塔架在地震发生前后的峰值位移云图进行对比分析，并针对应变能峰值进行研究。地震发生前，工况2的峰值位移明显高于工况9和工况10，说明低风速湍流风造成的结构位移响应更剧烈；地震发生后，工况2的峰值位移响应减小，而工况 9和工况10的峰值位移响应明显增加。工况10的峰值位移响应明显高于工况2和工况9，说明高气动载荷造成的气弹阻尼效应可有效减小地震载荷导致的塔架位移响应幅值。由图15可知，气弹阻尼效应同样可以有效缓解应变能堆积，加速结构遭受地震载荷后蓄积于结构形变中的能量耗散。

图15 变湍流风载荷塔架应变能云图

3.3 波浪载荷

对变波浪载荷结构时域响应结果进行对比分析，结果如图16所示。从图16可以看出，没有地震发生时，波浪载荷的变化对结构产生影响较小，湍流风载荷对结构各响应起主导作用。地震发生后，波浪载荷变化导致地震作用下结构动力学响应增加。工况2与工况13各响应相差较小，说明波浪载荷较小时，可以忽略不计，但随着波浪载荷的加剧，地震作用下的结构响应加剧。

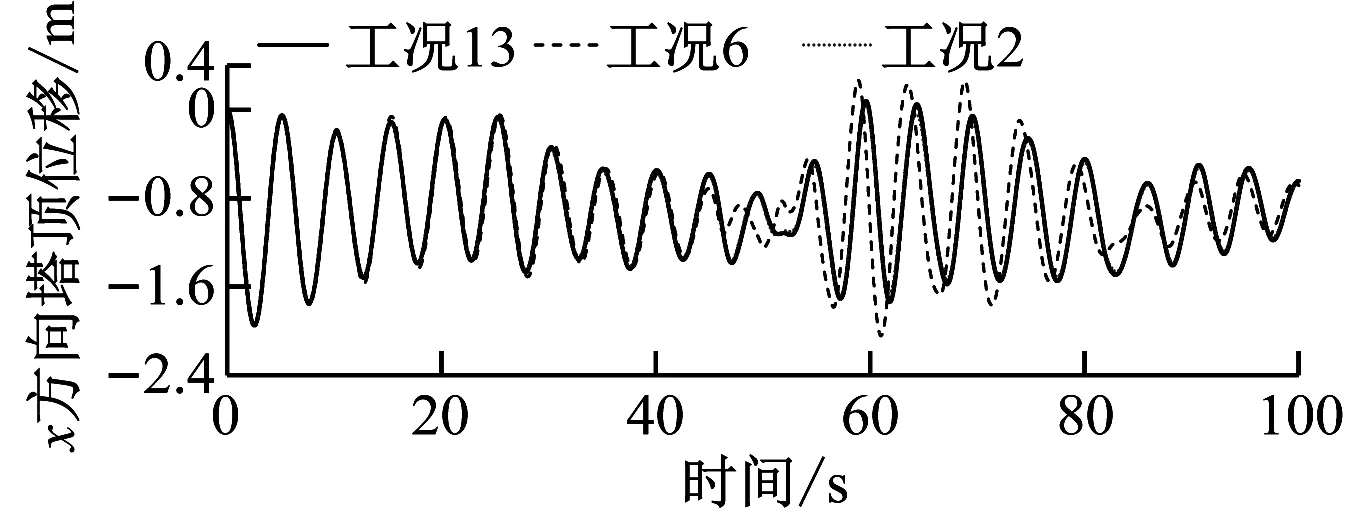
(a)

分析图17可知，各工况应力峰值时刻并无明显差异，但与其他2个算例相比，工况 6的应力值有明显变化，其节点应力峰值为236.4 MPa；而工况 2和工况 13分别为191.2 MPa和196.6 MPa，相差约23.6%。考虑到不同支撑结构对波浪载荷的敏感性不同，以及海水深度的增加所造成的影响，对固定式海上风力机各结构制定详细的标准时，波浪载荷不可忽略。

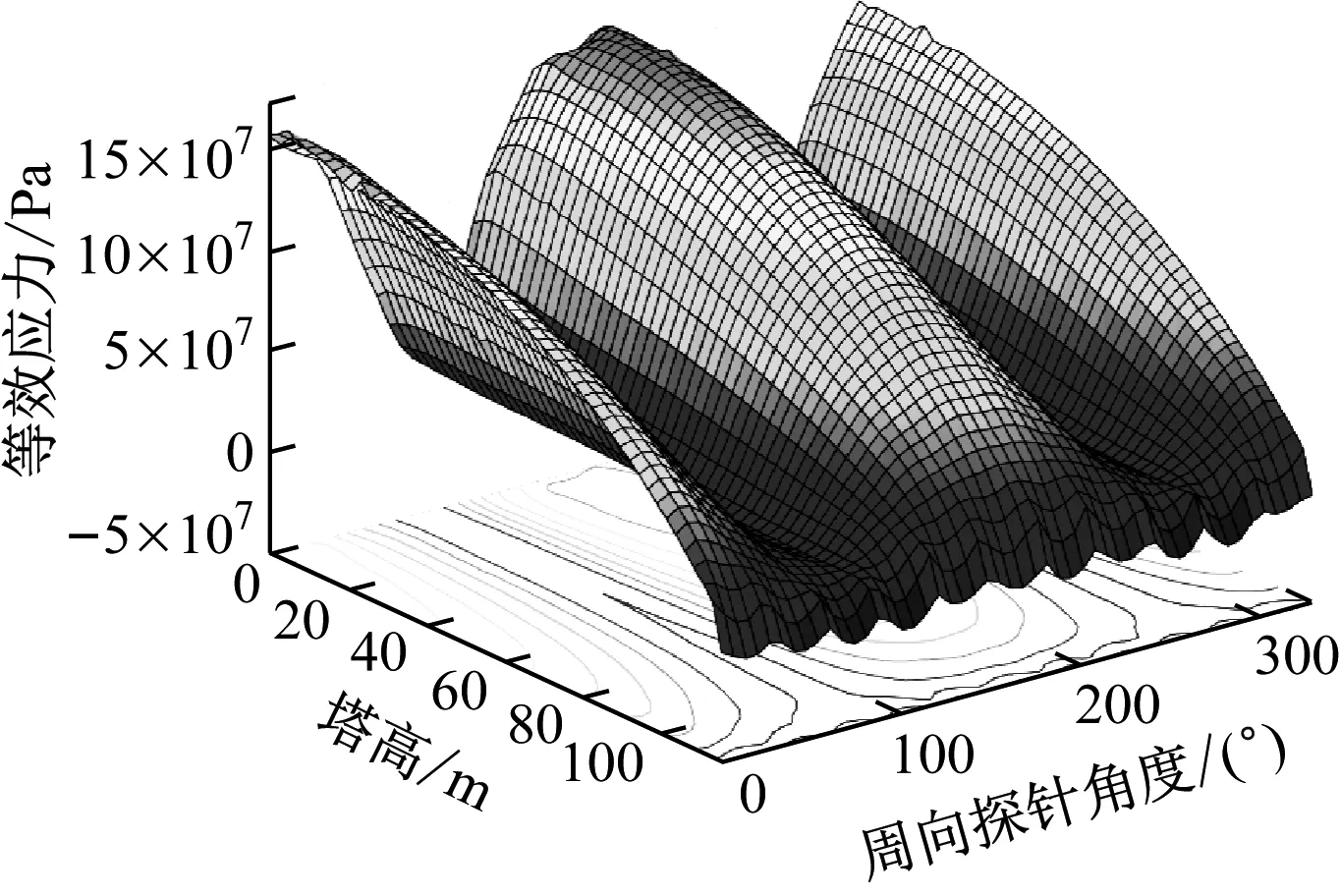
(a) 工况2-61.60 s

图18给出了变波浪载荷条件下峰值时刻塔架位移云图，其中左边3个图是未发生地震载荷时的位移云图。图19给出了变波浪载荷条件下峰值时刻应变能云图。由图18和图19可知，塔架的位移响应依然保持以一阶模态为主的塔顶俯仰运动，而波浪载荷的变化仅对工况 6在61 s峰值时刻的位移产生一定影响，但影响较小，说明波浪载荷的变化化对结构位移影响较小。应变能蓄积位置依然保持在塔底向上26 m的位置附近，但幅值分布差异十分明显，工况6的应变能幅值高于1 980 J的区域明显大于工况2和工况13，说明波浪载荷对塔基应变能影响较大。因此，波浪载荷对结构的影响集中于结构底部受波浪及海流冲击较近的位置。地震能量由桩基自下而上传递，所以波浪载荷变化在一定程度上影响地震能量自桩基向结构上部传递的过程，从而导致结构动力学响应的变化。

图18 变波浪载荷塔架位移云图

图19 变波浪载荷塔架应变能云图

4 结 论

(1) 由于风、浪、流载荷的瞬态特性，风力机结构的动态响应随环境载荷变化波动较大。支撑结构动态响应规律主要呈现塔顶前后及横向的往复运动。

(2) 风、浪载荷导致结构横向和纵向各响应增幅小于地震载荷。结构横向响应受风、浪、流载荷和气弹效应影响更显著。地震冲击下，各方向响应迅速增加，同时会放大风、浪、流载荷对结构的作用。

(3) 在承受风、浪、流及地震载荷时，结构塔基处应力激增和应变能的蓄积说明此处结构失效风险较高。

(4) 不应仅从塔顶或塔基的宏观时域响应判断是否有考虑该环境载荷的必要性。动力学响应分析应考虑气弹效应对结构位移响应的影响和浪、流载荷引起的支撑结构局部应力增幅。湍流风载荷和浪、流载荷在研究风力机地震动力学响应时不可忽视。