基于CEEMDAN样本熵与卷积神经网络的轴承故障诊断
肖俊青, 金江涛, 李 春, 许子非, 孙 康
(上海理工大学 能源与动力工程学院,上海 200093)
滚动轴承作为旋转机械的重要基础部件,极易出现磨损和损伤[1]。由于滚动轴承长期处于变负载、摩擦以及非稳定冲击等工况下,如果对于早期微小故障不及时排查并处理,极易引发灾难性事故[2]。因此,需要对滚动轴承的运行状态进行有效监测和诊断,确保转动系统长期高效、稳定、安全地运行。
滚动轴承故障诊断方法大多基于振动信号分析,而常用的振动信号处理方法主要包括时域分析、频域分析和时频分析[3]。由于采集的振动信号具有大量噪声,早期有效故障信息极易被噪声淹没,导致采用传统时域分析和频域分析方法难以获取有效的特征信息[4],而时频分析方法被广泛应用于含噪信号的故障特征提取,且取得了一定效果[5-6]。
在实际工程中,经验模态分解(EMD)算法虽然优于小波分解算法,但存在过包络、欠包络以及因包络极值点误差引起的模态混叠和端点效应等问题[7]。Smith[8]提出了局部均值分解(LMD)算法,可较好地抑制端点效应,但包络线难以准确拟合振动信号序列的趋势。Torres等[9]提出的自适应白噪声平均总体经验模态分解(CEEMDAN)算法可有效地将振动信号突变分解为高频本征模态函数(IMF)分量特征,但难以避免冗余分量的干扰。样本熵可作为衡量时间序列复杂度的指标,已被广泛应用于信号处理,并取得了良好的效果[10-11]。
随着机械设备朝着大型化、数字化和智能化方向发展,其产生的高维、海量数据促使数据挖掘与故障诊断技术逐渐成为重点研究方向。卷积神经网络(CNN)作为深度学习的典型代表,凭借其可学习自身特性、自适应提取特征信息并进行故障识别的优势,被广泛应用于故障诊断领域[12-13]。CNN智能诊断与数据预处理方法相结合虽然可以有效处理海量、高维数据,避免环境噪声干扰和准确率低的问题,但在准确筛选最优IMF分量方面存在明显不足,而分形盒维数[14]能够较好地描述振动信号的复杂性和非线性特征,具有良好的抗噪性,可作为最优IMF分量的筛选指标。
笔者基于分形理论,提出将CEEMDAN样本熵与CNN联合的故障诊断方法。采用CEEMDAN算法对强噪振动信号进行分解,通过分形盒维数筛选最优IMF分量,计算其样本熵,并输入到CNN中进行故障诊断,不仅可避免冗余分量的噪声干扰,还能进一步提高CNN故障识别分类的准确性。
1 基础算法
1.1 CEEMDAN算法
CEEMDAN算法从2个方面解决了集成经验模态分解(EEMD)和互补集成经验模态分解(CEEMD)算法存在的模态混叠和残留噪声问题,即将高斯白噪声加入经EMD算法处理后的含噪IMF分量中,避免直接添加在振动信号中易出现余噪的影响。CEEMDAN算法摒弃了对EMD分解后的IMF分量总体进行平均,而是对第一阶IMF分量就进行总体平均计算,直到获取最终第一阶IMF分量,并对残余部分重复以上操作,有效解决了噪声从高频到低频转移传递的问题,提升了分解过程的完备性。CEEMDAN算法步骤如下:
(1) 将正负成对的高斯白噪声加入到振动信号中并进行分解。
E(z(t)+(-1)qφvi)=C1(t)+r1(t)
(1)
式中:E()为EMD分解后的IMF分量;z(t)为振动信号;t为时间;φ为噪声标准差;vi为满足标准分布的高斯白噪声信号;q为添加的正负噪声;C1(t)为第一阶IMF分量;r1(t)为残余信号。
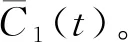
(2)
(3) 计算并消除第一阶IMF分量的残余信号。
(3)
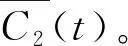
(4)
(5) 计算并消除第二阶IMF分量的残余信号r2(t)。
(5)
(6) 重复上述步骤,直到残差信号为单调函数,不能继续分解,则算法结束。此时,振动信号z(t)被分解为
(6)
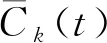
1.2 样本熵
样本熵是对近似熵改进的算法[15],既具备近似熵优点,又避免了自身匹配和模板匹配的繁琐,消除了近似熵中统计量不一致的难题。样本熵具体步骤如下:
(1) 设一个长度为M的时间序列,求长度为l和s两向量Zm(l)与Zm(s)对应标量之间的最大距离d(Zm(l),Zm(s))。
式中:z()为长度为M的时间序列;l=1,2,…,M;s=1,2,…,M;k=1,2,…,m-1,其中m为时间序列的维度。
(2) 设定阀值p,计算两时间序列在m点处的匹配概率Bm,l(p)。
Bm,l(p)=Am,l(p)×(M-m)-1
(8)
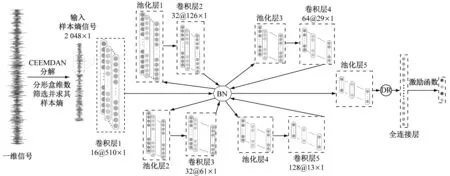
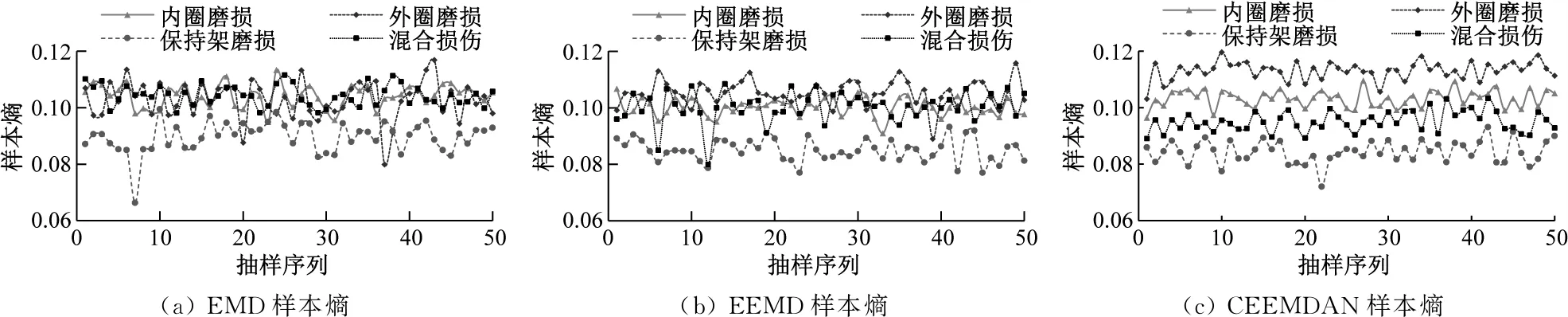
式中:Am,l(p)为d(Zm(l),Zm(s)) (3) 求匹配概率Bm,l(p)的均值Bm(p)。 (9) (4) 将序列重构为m+1维向量,重复步骤(1)~步骤(3),得到Bm+1(p)。 (5) 求长度为M的样本熵SampEn(m,p,M)。 SampEn(m,p,M)=-ln[Bm+1(p)×Bm(p)-1] (10) 分形维数能够客观地量化描述振动信号的细节特征和复杂性,解决滚动轴承非线性振动信号特征值难以筛选的难题,而其中分形盒维数最为常见[16]。由于分形盒维数自身的不规则性和系统具有填充空间能力,采用边长为ε的盒子对分形对象进行填充,通过逐渐缩小ε和增加盒子数目N(ε)来提高填充度,并采用最小二乘法对N(ε)与ε构成的双对数坐标曲线进行拟合,其斜率即为分形盒维数D。 (11) N(ε)=1/ε (12) CNN模型不仅具有深度结构前馈神经网络,还具有在时间或空间下采样、局部连接和共享参数的优势,可减小训练参数量、缩减数据维度和避免算法过拟合[17],而其“端到端”的数据处理方法可增强多个隐含层自主学习分层特征的能力,避免特征提取过程中人为过多干预影响故障诊断的准确率[18]。CNN模型一般包含卷积层、池化层和全连接层,经多层卷积层交叠形成深度卷积网络结构[19]。CNN模型经典结构见图1。 图1 CNN模型经典结构 经过堆叠卷积和池化后,利用提取的特征通过Softmax分类器对全连接层结果进行分类输出。由于丢弃(DR)正则化技术[20]与神经网络训练流程相贴合,可忽略隐藏层的部分单元,以防止过拟合现象。全连接层中具有多层感知机的隐含层,可较好地整合卷积和池化后的数据信息,提高CNN模型的泛化性[21]。 强噪环境下轴承振动信号异常复杂,难以准确提取故障特征, 虽然CNN模型能够从原始数据中挖掘抽象且有效的故障特征,但容易出现信息缺失、提取不充分和噪声干扰等问题。目前,虽然普遍采用时频分析方法对原始振动信号进行预处理,再输入CNN模型进行故障诊断,但仍无法彻底消除余噪干扰。为此,笔者基于分形理论,提出CEEMDAN样本熵与CNN联合故障诊断方法(即CEEMDAN样本熵-CNN方法),其故障诊断流程见图2,具体步骤如下: 图2 故障诊断流程图 (1) 采集滚动轴承各故障状态下的振动信号。 (2) 对振动信号进行预处理,将各故障状态下的振动信号进行CEEMDAN分解,获取各IMF分量。 (3) 计算不同故障下各IMF分量的分形盒维数,筛选出最优IMF分量。 (4) 计算最优IMF分量的样本熵,构建故障特征向量。 (5) 将故障特征向量输入CNN模型,实现故障诊断与分类。 数据采集过程中难以避免引入大量噪声,导致CNN模型在训练不同卷积核时,无法准确区分隐含层中的故障特征,诊断准确率较低。采用CEEMDAN样本熵-CNN方法可滤除振动信号中部分噪声,增强故障识别能力及泛化性能。CEEMDAN样本熵-CNN方法简图见图3。由图3可知,采用小尺寸卷积运算可更好地简化计算;而在多层卷积与池化之间循环使用批量归一化(BN)方法,并在全连接层前进行DR处理,可有效避免诊断过程中产生过拟合现象,提高故障识别率[22]。 图3 CEEMDAN样本熵-CNN方法简图 如图4所示,轴承加速寿命测试平台由交流电动机、液压加载系统、转速控制器、滚动轴承、转轴和加速度传感器构成[23],用于监测各工况下轴承的全寿命实时数据。将试验工况的采样频率设定为25.6 kHz,转速设定为2 100 r/min和2 250 r/min。 图4 轴承加速寿命测试平台 滚动轴承的故障信号由固定在轴承竖直方向和水平方向上的加速度传感器获取,其试验工况见表1。 表1 轴承试验工况 内圈磨损、混合损伤、外圈磨损以及保持架磨损故障下的幅值时域图见图5。由图5可知,虽然不同故障下的幅值时域图存在一定差异,但以此作为特征信息直接进行故障诊断,无法保证其准确性和可靠性。因此,需结合相应的预处理方法,突显振动信号中的非线性特征,提高有效故障特征的提取能力。 (a) 内圈磨损 为更贴近实际应用,验证所提CEEMDAN样本熵-CNN方法的有效性,对试验故障数据进行分析。限于篇幅,仅采用EMD、EEMD和CEEMDAN分解内圈磨损的振动信号,结果见图6。由图6可知,采用EMD分解时在低频IMF分量存在明显的模态混叠;采用EEMD分解虽然可在一定程度上抑制模态混叠,但容易产生多个虚假IMF分量,造成振动信号失真,且无法消除高斯白噪声的传递问题;而CEEMDAN算法是自适应地对振动信号添加高斯白噪声,可较好地消除其传递对分解结果的影响,但仅从分解结果无法准确选取最优IMF分量。 (a) EMD分解结果 为获取最优IMF分量,需计算各IMF分量的分形盒维数,为验证其可靠性,随机筛选各IMF分量的100个样本,求取分形盒维数均值,如表2所示。 表2 不同算法下IMF分量的分形盒维数 分形盒维数越小,振动信号越规则,包含的故障特征越明显,越有利于提高故障识别率。因此,选取分形盒维数最小的IMF分量,但因其尚存少量残余噪声,因此求其样本熵作为CNN模型输入的特征向量。为突显所提方法的优越性,分别与EMD样本熵和EEMD样本熵进行对比,结果如图7所示。 由图7可知,在4种故障状态下,CEEMDAN样本熵较EMD样本熵和EEMD样本熵具有更显著的区分度。因此,将CEEMDAN样本熵作为CNN模型的输入可较好地消除IMF分量残余噪声的影响。 图7 不同算法下的样本熵对比 为更符合实际工况,考虑混杂噪声对轴承振动信号故障诊断准确率的影响。为此,在振动信号中添加不同信噪比的高斯白噪声,进一步验证CEEMDAN样本熵-CNN方法的实用性和可靠性。将试验故障数据划分为训练集、测试集和验证集,并对其进行重采样,以增加样本数量。每次从各故障样本中随机选取训练集800组、测试集100组、验证集100组,迭代100次。将CEEMDAN样本熵-CNN方法与EMD-CNN方法、EEMD-CNN方法和CEEMDAN-CNN方法进行对比。为避免试验结果的偶然性,在不同方法下运算10次并取其均值,结果见表3。由表3可知,信噪比对各方法准确率的影响较显著,其值可较真实地反映轴承实际工作环境。信噪比越低,表明振动信号采集环境越恶劣,其对故障识别性能的影响越大;CEEMDAN样本熵-CNN方法可有效排除CEEMDAN算法在分解过程中残余噪声的影响,突显故障信息、提高特征提取能力和识别性能,较EMD-CNN方法、EEMD-CNN方法和CEEMDAN-CNN方法在不同信噪比下均具有较大优势,而深层网络结构更有利于处理大数据,进行故障诊断识别和分类。 表3 各信噪比下不同方法的准确率对比 由于深层网络学习大多基于数据本身的属性,缺乏详细深入的故障类型分类,限于篇幅,仅给出CEEMDAN样本熵-CNN方法在不同信噪比下的t-SNE聚类可视化分析结果,如图8所示。由图8可知,经深层网络处理的数据采用t-SNE聚类可视化可较好地对不同故障进行分类。随着信噪比的增大,环境噪声减弱,分类效果逐渐突显。在信噪比为6 dB时,保持架磨损故障已被完全分离,其他故障也有较好的聚类效果。 (1) 采用CEEMDAN样本熵作为输入的特征向量,不仅可以滤除部分噪声,还能避免冗余分量噪声的干扰,提高了特征向量输入的准确性。 (2) 相比现有方法,CEEMDAN样本熵-CNN方法在不同信噪比下均具有较高的准确度,表现出良好的分类和识别性能。 (4) 对所提CEEMDAN样本熵-CNN方法得到的结果进行t-SNE聚类可视化,可使其结果更具直观性与实用性。1.3 分形盒维数
1.4 CNN基本原理

2 诊断流程
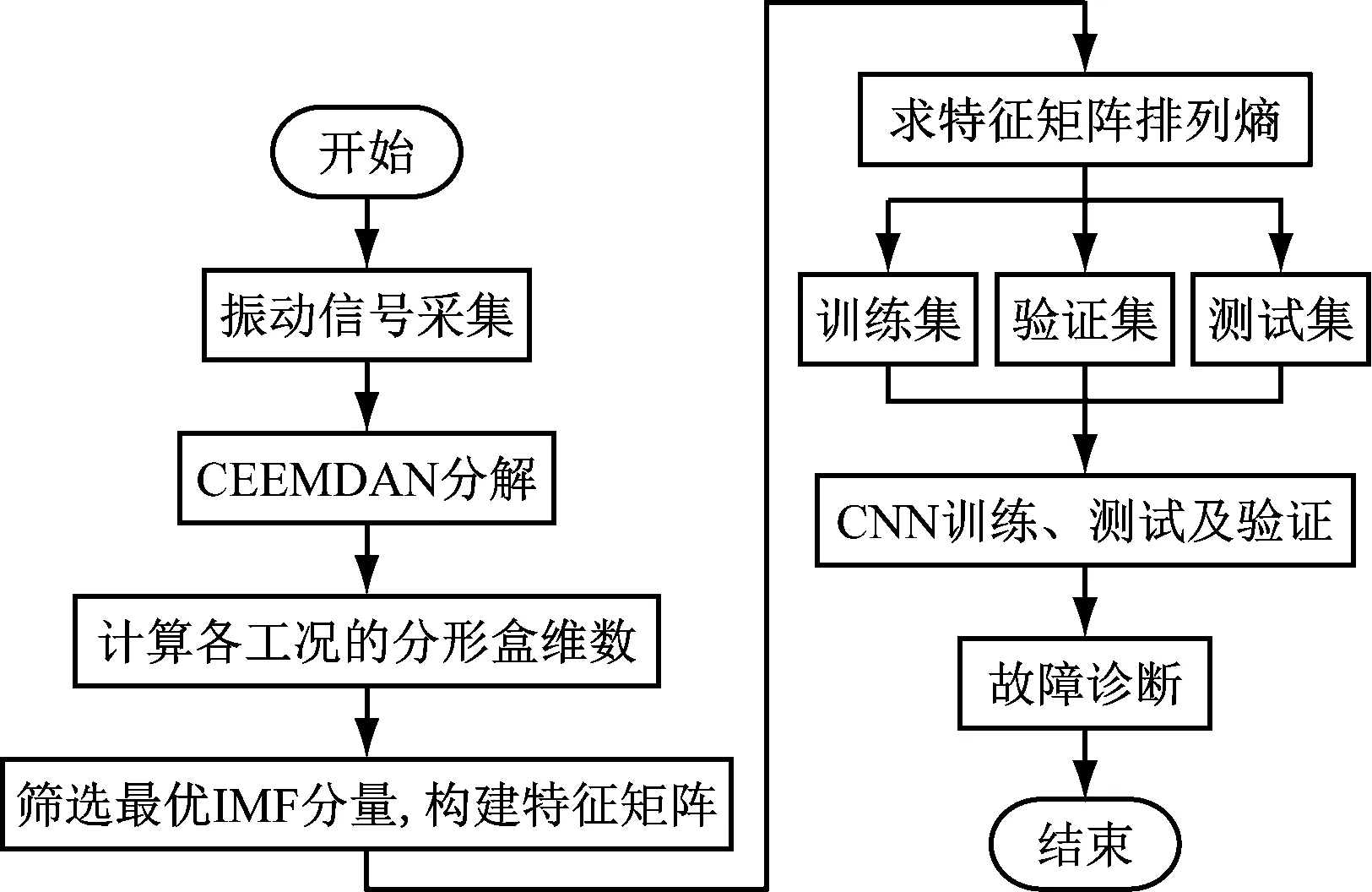
3 试验验证
3.1 试验参数

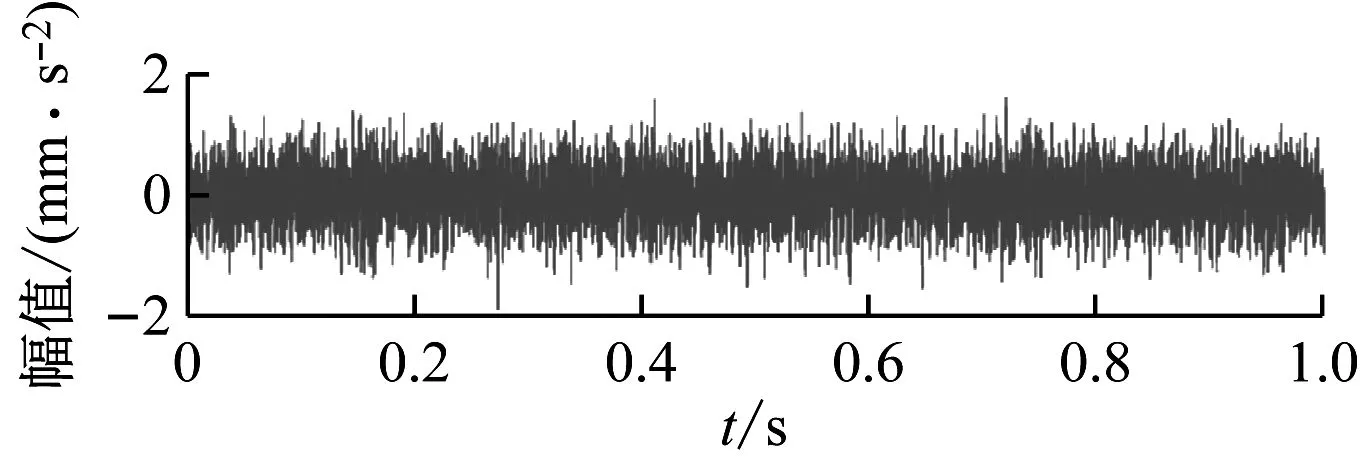
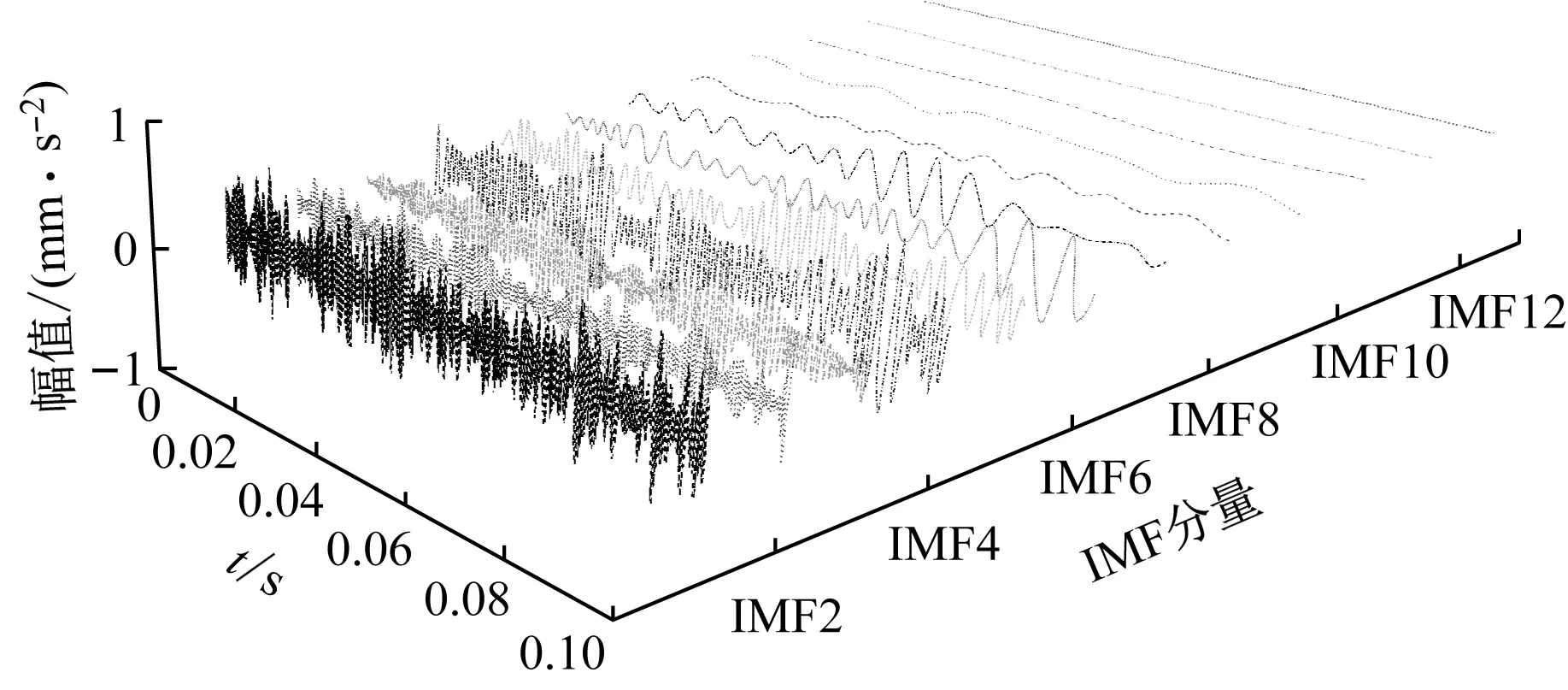
3.2 分形特性与样本熵分析
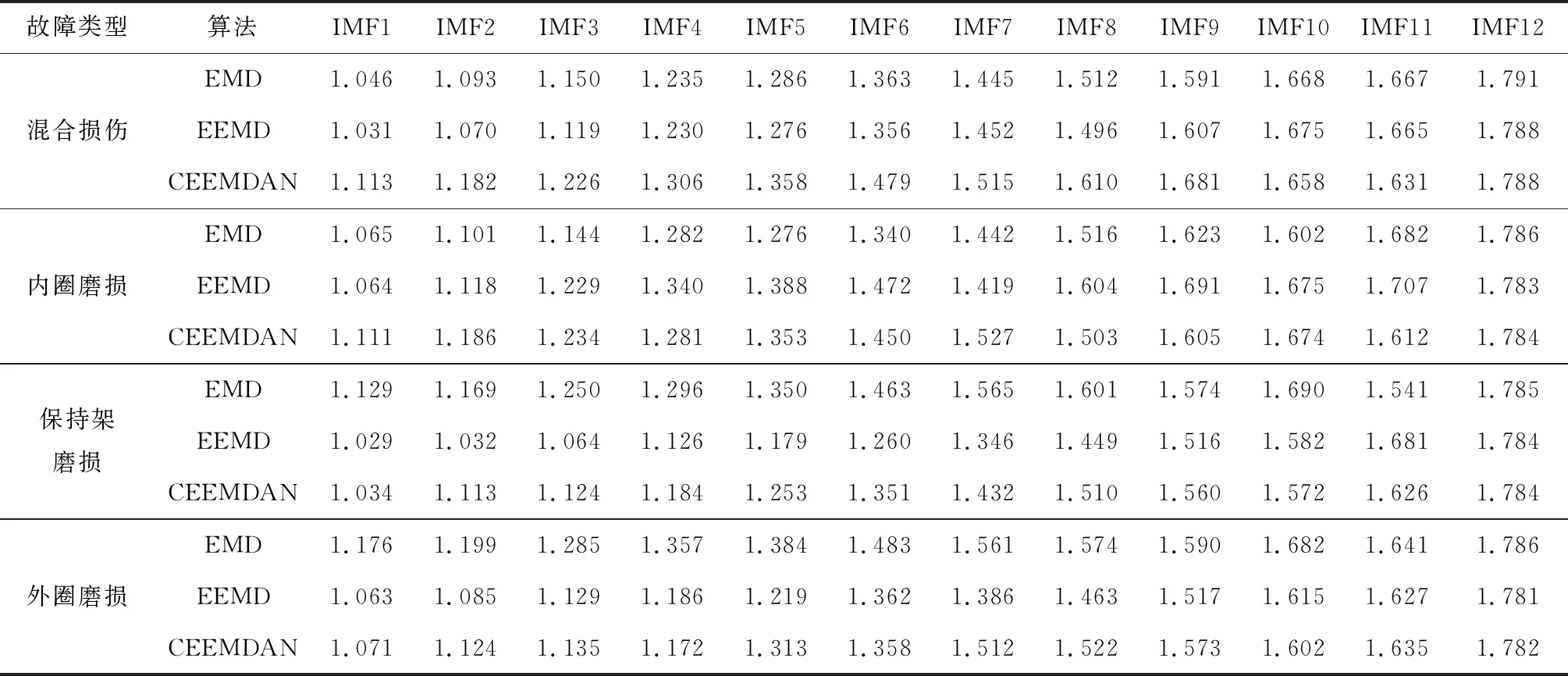
3.3 CEEMDAN样本熵-CNN方法

3.4 t-SNE聚类可视化分析
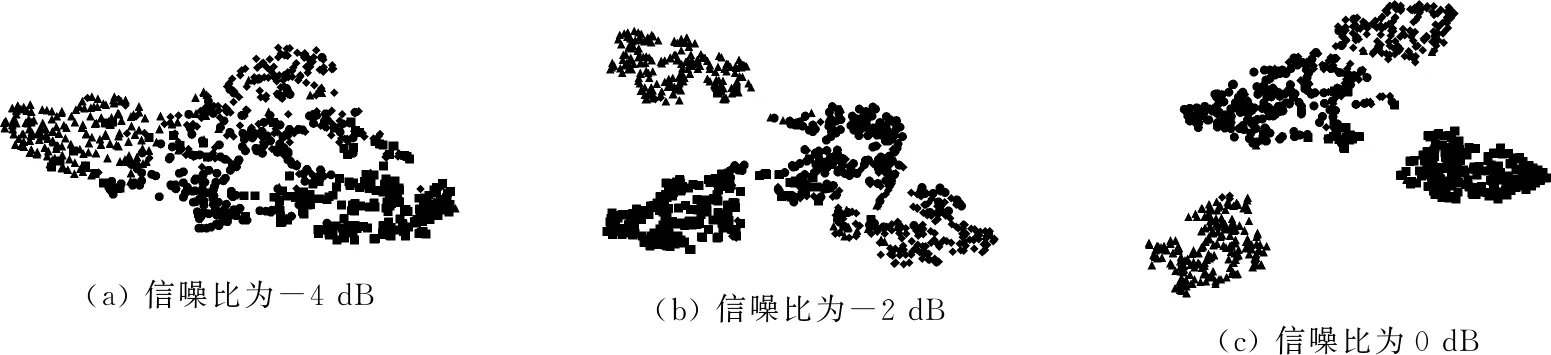
4 结 论

