基于POI和主动学习的城市功能区分类方法研究

杨 鑫，杨宜来，胡克勇

(青岛理工大学信息与控制工程学院，山东 青岛 266525)

0 引言

城市功能区分类研究不仅对城市规划与管理具有十分重要的意义，还可为人类生活、工作和交通等提供便利[1]。现有城市功能区分类方法主要可分为：基于指标值阈值划定的方法、基于非监督的聚类方法和基于监督分类的方法[2-3]。基于指标阈值划定的方法受主观因素的影响较大，监督分类和非监督分类方法以数据为基础，分类结果相对客观。非监督分类方法实现简单，但分类结果准确性相对较低。监督分类法可从训练样本中获取先验知识以提高分类准确性，且训练样本越多，训练得到的模型也越准确。然而实际应用中，功能区训练样本数据通常较难获取，区域内主要功能的判断需要行业专家的专业知识及对城市深入地熟悉与了解。如何使用较少的训练样本来获取性能较好的分类器是分类方法选择要考虑的重要问题。

本研究提出采用POI数据和主动学习算法实现城市功能区分类。POI是电子地图上代表地理实体的点数据，具有易获取、数据覆盖面全、数据完整性高的特点[4]。主动学习是一种半监督分类法，其核心任务是确定选择训练样本的标准，从而选择尽可能少的样本进行标记来训练出一个好的学习模型，相对于监督分类方法，主动学习显著降低了训练样本收集的成本，该方法的应用有助于快速准确实现城市功能区分类。

1 研究区和数据

选择北京市朝阳区作为典型研究区。朝阳区是北京市主城六区之一，西与东城区、丰台区、海淀区相毗邻，北连昌平区、顺义区，东与通州区接壤，南与大兴区相邻；朝阳区是北京市辖区内人口较多的一个区，工业发达，外交活动频繁，在经济、居住、教育等方面均有较强代表性，基础服务设施完善，区域功能齐全且分化明显。

研究采用街区作为城市功能区的空间尺度。当前常用的城市功能区空间划分方法包括：街区(又称交通分析小区，Traffic Analysis Zone，TAZ)和不同空间尺度的格网[5]。格网常用于大致表征城市功能区的分布趋势，无法准确描述城市功能区；TAZ是由不同等级的道路连接、交叉形成的区域，区域内的功能相对比较完整。本文采用不同等级的道路将朝阳区划分为741个TAZ，如图1(a)所示。

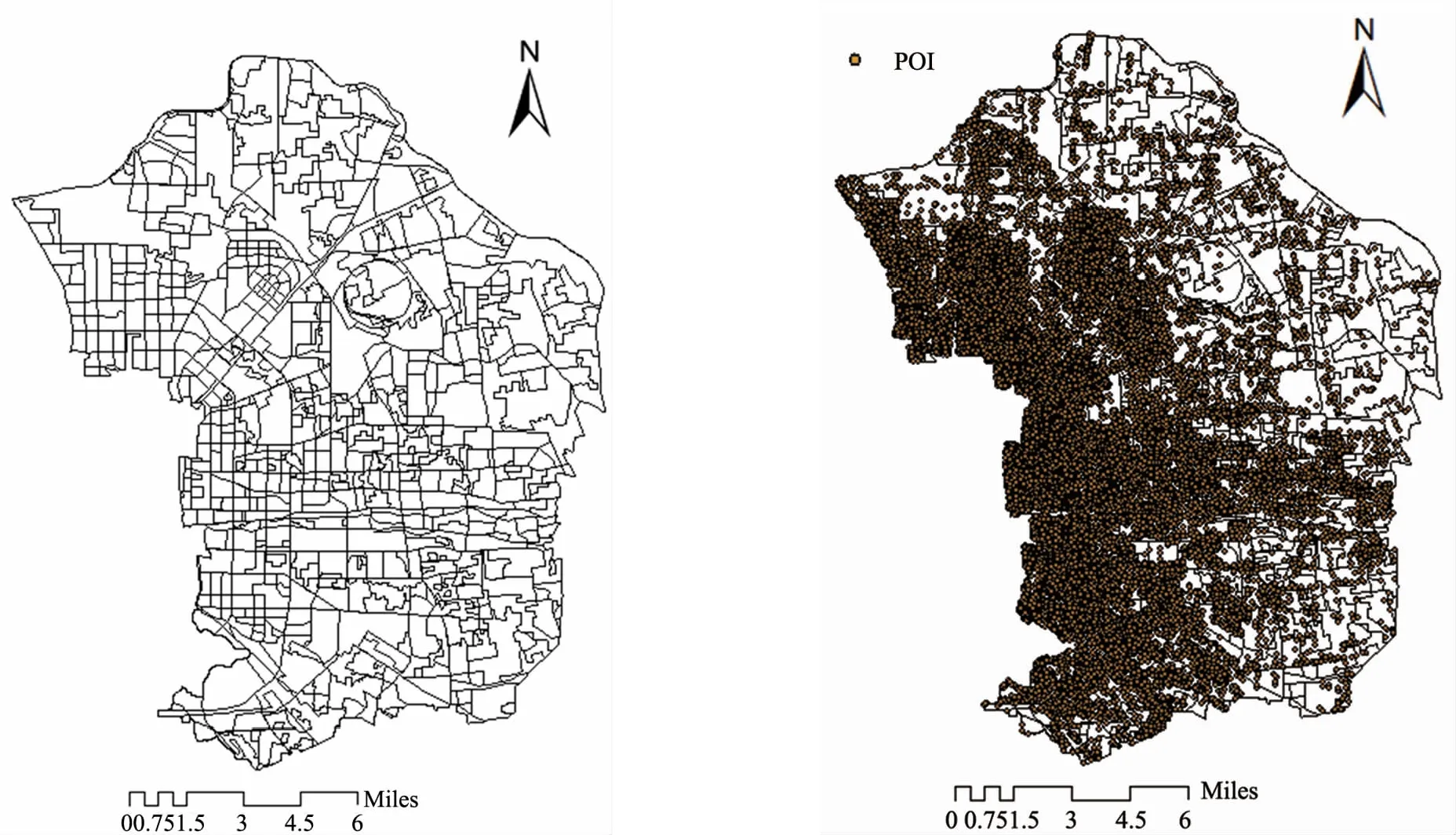
图1 北京市朝阳区街区及POI分布图

本研究所使用的POI数据通过百度地图API下载，共计90767条(见图1(b))，属性字段包括名称、类别、经纬度坐标。结合土地利用规划数据、POI、高空间分辨率遥感影像等数据，本研究对朝阳区所有TAZ的城市功能类型进行了人工识别，结果如图2所示，功能区类型包括：农地、休闲娱乐区、城中村、就业区、居住区、就业居住混合区。

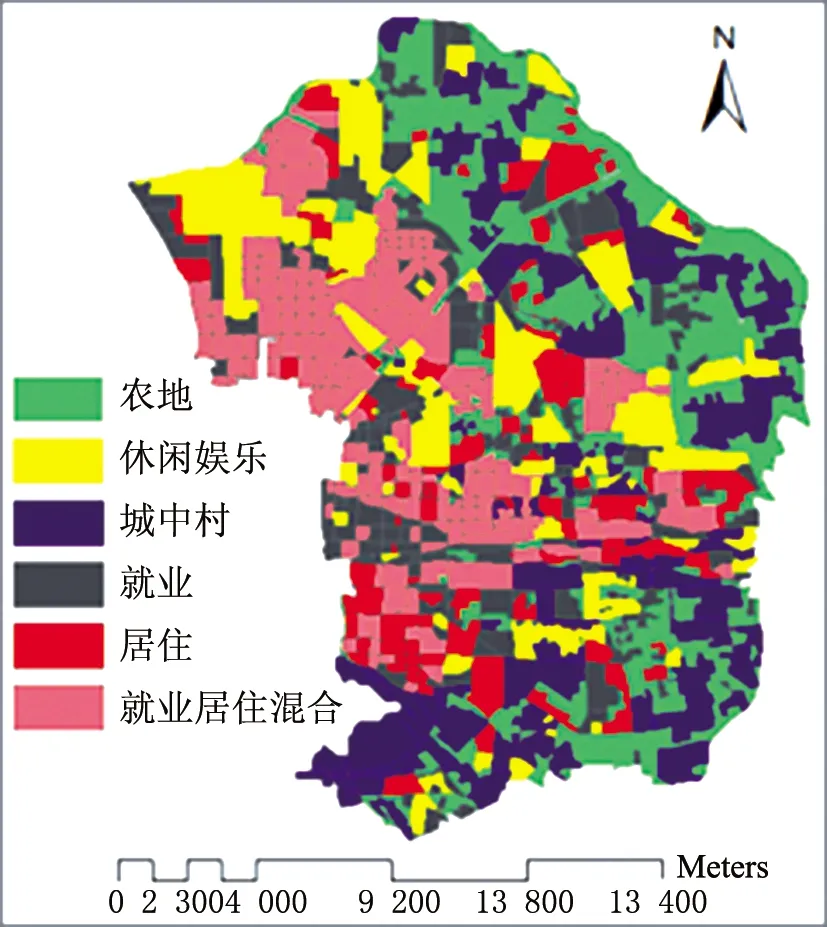
图2 人工功能区识别结果

2 研究方法

2.1 城市功能区分类指标体系构建

POI代表的地理实体或社会经济组织机构涵盖人们日常生活的方方面面，且具有详细的三级分类体系。根据POI类型与城市功能区类型的相关性及对城市功能区类型的影响作用，选择与城市功能区类型相关性较大的POI类别构建了城市功能区分类的指标体系，见表1。

表1 街区功能分类指标体系

表1中所有指标的计算方法如下：

(1)指标 A1～A6。计算该类指标首先需对街区内该类型的全部POI进行计数，计算过程：采用ArcGIS软件的Spatial Join功能，选择街区图层作为目标图层，连接需计算的POI类型数据到目标图层，即可在目标图层的属性表中得到街区内的POI计数。如果计数值大于0，则指标值为1，否则指标值为0。

(2)指标A7～A9。计算该类指标的过程如下：采用ArcGIS软件的Euclidean Distance 功能，输入需计算的POI数据和街区图层数据，即可计算得到街区内每个位置至与其最近的POI的距离；然后使用ArcGIS软件的Zonal Statistic功能即可计算得到街区内各位置距离值的平均值。

(3)指标 A10～A11。该类指标的计算过程为：采用ArcGIS软件的Spatial Join 功能，选择街区图层作为目标图层，连接需计算的POI类型数据到目标图层，即可在目标图层的属性表中得到街区内的POI计数，然后使用ArcGIS软件属性表管理中的Field Calculator功能计算街区内POI计数与街区面积的比值得到街区内该类POI的密度。

上述方法计算得出的不同指标之间存在数量级差，为消除数量级差带来的计算误差，对各个指标进行了均值标准化处理，由此得到与每个TAZ对应的11个指标。

2.2 基于主动学习算法的城市功能区分类

2.2.1 算法总体框架

主动学习算法是一个迭代的过程，每一次迭代从未分类数据集中选择最有价值的几个样本交由专家进行标记，并将这些新标记过的样本加入训练样本集，模型基于新的训练集进行更新，然后利用模型对未分类数据集中的样本进行分类，随后进入下一次迭代[6]。

采用主动学习算法对街区功能进行分类，每个街区就是一个待分类样本。每一次迭代过程中，所有街区可以分为三个类别：①已完成功能分类的街区，记为TK；②未完成功能分类的街区，记为TU；③被选中由专家标记功能类别的街区，记为TC。分类前TK为空集，TU为空时迭代终止，分类完成。

主动学习算法主要包含2个关键部分：一是抽样引擎，用于从TU中选择样本记入TC；二是分类器，用于根据现有训练样本集TK进行分类模型训练，完成TU中样本的分类。由于不同样本对于样本分类的学习模型的贡献度是不一样的，如果能够选取一部分最有价值的街区标记其类型，有可能仅基于少量数据就能获得同样高效的模型。因此在抽样引擎中设计合理的选择策略，选择最有价值的街区，是主动学习的关键任务。

本文设计一个基于密度峰值聚类的抽样引擎，采用密度峰值聚类方法确定TU中所有街区的价值排序，依次选择最有价值的街区记入TC，由专家标记其类别记入TK。然后基于该聚类方法的聚类优势设计一个基于标准投票策略的分类器，逐步完成TU中街区的分类。以下将详细阐述采用基于密度峰值聚类的主动学习算法实现街区分类的方法。

2.2.2 关键参数计算

本文采用基于密度峰值聚类的主动学习算法进行街区分类。密度峰值聚类方法由Rodriguez和Laio于2014年提出[7]，该算法的核心思想在于其对聚类中心的刻画，作者认为聚类中心应用同时具有以下两个特点：①样本的“局部密度”大，即它被密度均不超过它的邻居包围，②样本与其它密度更大的样本之间的“距离”相对更大。

将朝阳区所有街区记为集合X={X1,X2, ……,Xn}，根据2.1中街区功能分类的指标体系，每个街区具有11个属性值，街区i的属性值可记为{Ai1,Ai2, ……,Ai11}。

本方法中包含两个关键参数：样本的局部密度ρi和到高密度样本的最短距离δi。这两个参数的计算都基于样本之间的距离dij，该距离采用样本属性的欧式距离来度量，计算公式为：

(1)

其中，dij为样本i与样本j之间的距离，Aik为样本i的第k个属性值。

局部密度表达的含义为以某一样本为中心，在某一设定的距离范围内样本的个数。样本i的局部密度记为ρi，其计算公式如下式：

ρi=∑jf(dij-dc)

(2)

ρi表示以样本i为中心，距离为dc的范围内样本的数量；其中dc>0，是需指定的距离，称为截断距离，其值的大小取决于所有样本间距离的分布；f(x)为一个判别函数，当x≥0时其值为0，当x<0时，其值为1。

样本i到高密度样本的最短距离δi的计算公式如下：

δi=minj:ρj>ρidij

(3)

若样本i在全部样本中具有最高的局部密度，δi为样本i与其最远的样本间的距离，可用计算公式可表述为：

δi=maxjdij

(4)

对每个样本计算上述两个关键参数后，所有样本可表示为式(5)。

(5)

在密度峰值聚类算法中还需要计算得到一个重要中间结果：master树。其获取过程为：计算样本i到高密度样本的最短距离δi时，记录距离样本i最近的高密度样本，称为样本i的master，具有最高局部密度的样本的master为空。假定样本i从属于其master，然后根据这种从属关系构建一个树，在这个树中，样本i为其master的子节点，master为空的样本为根节点，如果存在多个master为空的节点，创建一个空节点作为这些节点的根节点。

2.2.3 城市功能区分类

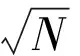
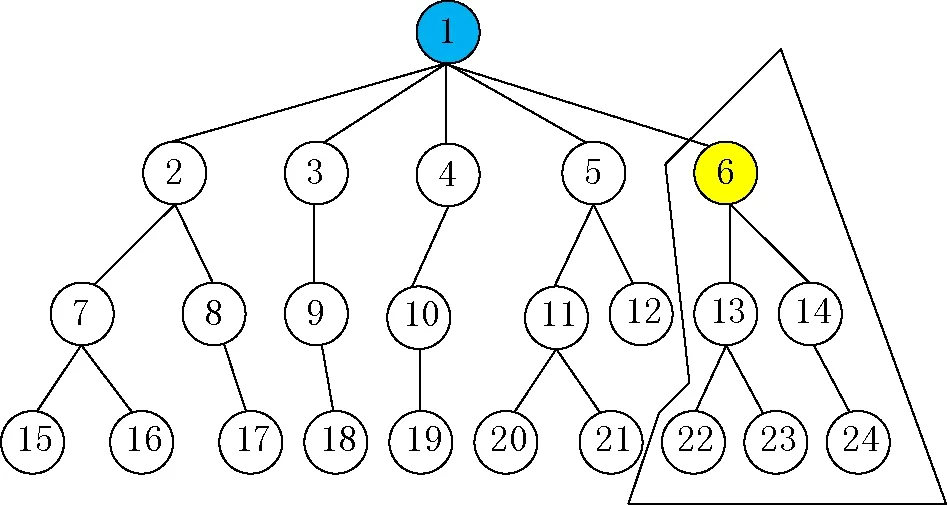
图3 聚簇标记、分离过程

对上述分离得到的两个新的集合再次调用主动学习算法。如图4所示，对两个新集合分别标记后，以样本6为根节点的集合已经是一个“纯集合”了，所以为这整个集合内的未标记样本分配与样本6、13、14一致的标签，如图4(b)中右子树。而以样本1为根节点的集合，再次分配标签后依然是“非纯集合”。如果还有标签可供使用，那么重复分离集合的过程，否则执行投票策略，如图4(b)中左子树。这里假设已经没有标签可用了，可见样本1、4的标签数量最多，故将样本1、4的标签分配给该集合内剩余未分配标签的样本。

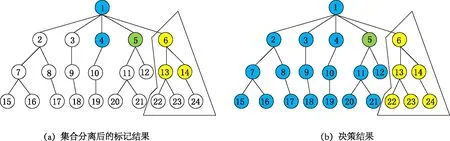
图4 “纯聚簇”与 “非纯聚簇”决策过程

当所有样本都被标记时，分类结束。如果标签用尽还有未被标记的样本，则需要使用投票策略对其进行分类，过程如下。统计未被全部分类的集合内的各个标签数量，找出数量最多的那种标签，将这种标签赋予本集合内所有未被标记的样本。至此，整个功能区分类过程全部结束。其算法描述如下。

主动学习算法：

初始化：输入全部待分类街区；

计算ρ和δ，构造一个 master树；

for(k=4; 专家标记样本的数量小于指定值N，且还存在未分类样本;k++)do：

基于密度峰值聚类，聚类类别数为k，依据 master 树，找到聚类中心和每个类别中包含的样本信息，同时根据聚类信息将 master 树分裂为k个子master树；

根据聚类中心和各类别信息，找出本轮循环的关键样本；

对关键样本的功能类型进行标记；

for(i=1 tok)do：

if第 i 个 master 树中的样本的功能类型没有完全标识 then：

如果该 master 树中已知类型的样本数量大于等于N，且已知类型完全一致，那么按已知样本类型来设置该 master 树中所有样本的类型；

end if

end for

end for

if还有样本未分类 then：

for(i=1;i≤k;i++)do：

如果第i个 master 树中还存在未分类样本，则采用标准投票策略决定未分类样本的类别；

end for

end if

3 应用研究

3.1 功能区分类结果

采用基于POI和主动学习的城市功能区分类方法，设置2.2.2中截断距离dc的值为3.5，设定标注功能区个数为50(占总功能区个数的6.75%)，依据图2中的功能区类型标记样本，完成北京市朝阳区所有街区分类，分类结果如图6所示。对比图2和图5可见，基于本方法实现的城市功能区分类结果与人工识别结果较为相似。休闲娱乐区在整个朝阳区分布较为均衡；农地、城中村主要分布在朝阳区的东部区域；就业、居住和就业居住混合区主要分布在西部区域，这与北京市的圈层结构以及朝阳区所处的地理位置密切相关，朝阳区东与通州区接壤，西则与发展更为成熟的东城、丰台、海淀相毗邻。

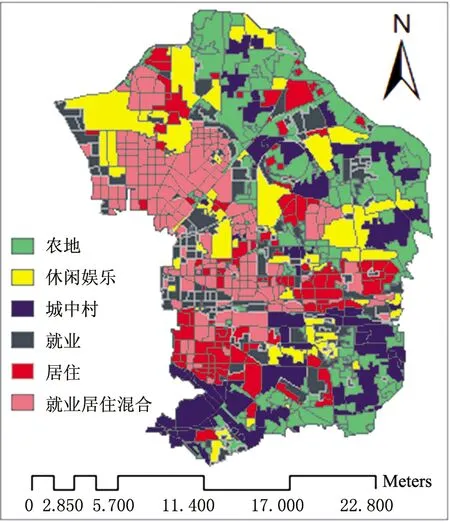
图5 功能区识别结果

3.2 结果分析与讨论

为分析采用基于POI和主动学习的城市功能区分类方法进行北京市朝阳区城市功能区分类结果的准确性，首先本文选择了几个区域，将识别结果与百度地图和百度卫星地图进行了对比分析，见图6。区域A为国家体育馆(鸟巢)附近的几个街区，结合百度地图和百度卫星地图，可以看到(1)区域A左侧为国家森林公园，本方法的识别结果为休闲娱乐区；(2)区域A右侧的街区内均包含了居住小区、商业大厦、幼儿园、中小学，居住就业功能都非常成熟，本方法的识别结果为就业居住混合区。可见，区域A内城市功能区识别情况与实际相符。区域B为古塔公园附近的几个街区，从该区域的百度地图和百度卫星地图可以看出该区域内功能类型复合多样，结合地图：(1)识别结果中被识别为休闲娱乐区的两个街区分别是北京CBD国际高尔夫球会和古塔公园；(2)识别结果中被识别为居住区的街区是观音惠园和北京安德鲁斯庄园这两个居住小区；(3)识别结果中被识别为就业区的街区从卫星地图上可见为工厂厂房；(4)识别结果中被识别为城中村的街区是王四营乡和观音堂村。可见，区域B内城市功能区识别情况与实际相符。

图6 部分区域识别结果与百度地图和百度卫星图的对比

区域C为富力城附近几个街区，从识别结果是可以看出该区域内主要包含居住区和居住就业混合区，从百度地图和百度卫星地图上可见该区域内主要是成熟居住区和商务区，幼儿园、中小学等配套生活设施齐全，这表明该区域内的功能区识别总体准确。然而，该区域内道路密集、街区面积较小，采用本方法的识别过程中相邻街区的功能可能相互影响，从而造成部分功能区识别结果与人工识别结果之间存在一定偏差，如区域C的识别结果上以星号标注的居住区，其人工识别结果为就业居住混合区，分析该街区的指标计算结果发现其离幼儿园、中小学的距离较小，与居住区的该类指标相近。

为了进一步分析本方法识别结果的准确性，计算了人工识别结果与基于本研究构建方法的分类结果之间的混淆矩阵，如图7所示。本研究中城市功能区分类对象为街区，分类过程中未考虑街区的面积，在进行识别结果的准确性评价时，应以功能区的个数为依据，而非以功能区的面积为依据，因此混淆矩阵中的值为街区个数的比例。

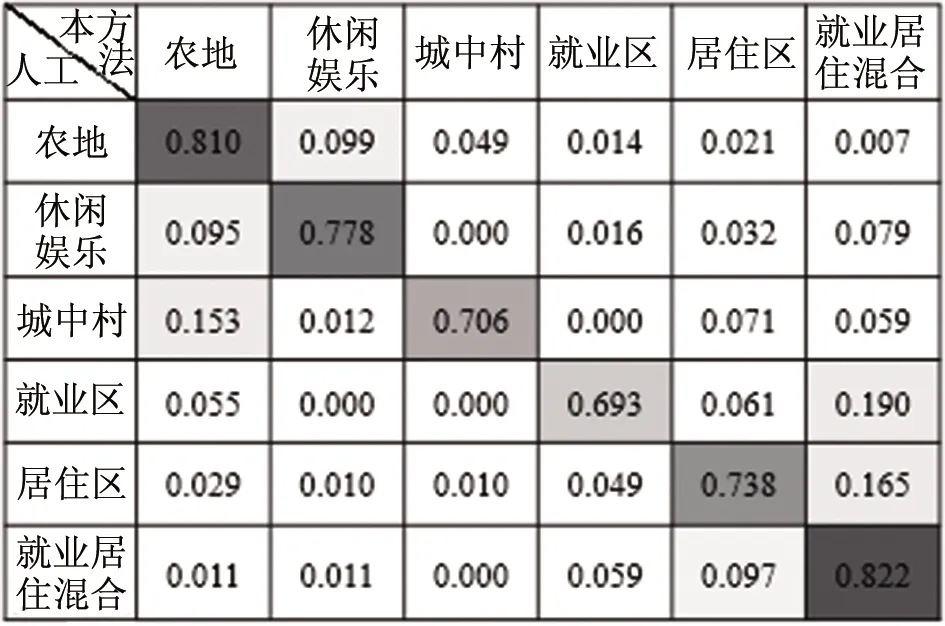
图7 识别结果混淆矩阵

从图7的混淆矩阵可见，本方法在城市功能区分类的应用中具有较高的精度，其中，农地和就业居住混合区的识别精度较高，分别为0.810和0.822；休闲娱乐区的居住区的识别精度其次，分别为0.778和0.738；城中村和就业区的识别精度相对较低，分别为0.706和0.693。

混淆矩阵中未正确分类的功能区，结合它们的POI分布情况及指标体系，对分类错误的原因进行了综合分析：

(1)图7的混淆矩阵显示未被正确识别的农地主要被识别为休闲娱乐区，未被正确识别的休闲娱乐区主要被识别为农地；未被正确识别的城中村主要被识别为农地。这主要是因为农地内包含的POI较少，而少部分休闲娱乐区和城中村内包含的POI也较少，且农地、休闲娱乐区和城中村都离幼儿园、中小学的距离较远，从而导致这三类功能区之间存在分类错误的情况。

(2)图7的混淆矩阵显示未被正确识别的就业区主要被识别为就业居住混合区，未被正确识别的居住区主要被识别为就业居住混合区，未被正确识别的就业居住混合区主要被识别为居住区，且这三类错误率相对较高。可见，这三类功能区类型相对容易混淆。分析就业区和居住区的POI分布情况发现，并非所有的就业区内完全不包含居住功能，也并非所有的居住区内完全不包含就业功能。在图6区域C中分类错误原因分析中，已阐述相邻街区的功能类型可能对当前街区的类型产生一定影响。另一方面，在设计基于POI的城市功能区分类指标体系时，考虑到POI仅能代表地理实体的类型，不能代表地理实体的功能强弱，比如，占地面积较大的住宅小区和占地面积较小的住宅小区反映在数据上都是一个POI点，同一个地理实体可能对应多个POI，如一个住宅小区可能在不同的出入口都包含一个POI点，因此，本研究中指标A1～A6设计为是否含有住宅、商务写字楼、产业园等POI，未考虑这几类POI数量或密度对功能区分类的影响，由此也导致部分识别结果的不准确。

3.3 截断距离对分类精度的影响分析

采用本文的方法进行城市功能区分类过程中，高密度样本的选择对分类结果至关重要，而截断距离dc是影响样本密度的重要因素，当dc过大时所有样本的密度值都较大，而当dc过小时所有样本的密度值都较小。因此，本文以北京市朝阳区为例，根据街区之间距离值的分布范围设置不同的dc完成城市功能区分类，探究dc与城市功能区识别总体精度的关系，分析结果见图8。其中，总体精度的计算以人工识别结果为标准(见图2)，统计本方法的识别结果中分类正确的功能区数量占功能区总数的比例。根据图5可见，当dc的取值小于2.5时，随着dc的增加分类精度总体上呈上升趋势；当dc的取值在2.5到8.5之间时，dc的变化对分类精度的影响较小；当dc的取值大于8.5时，随着dc的增加分类精度呈下降趋势。

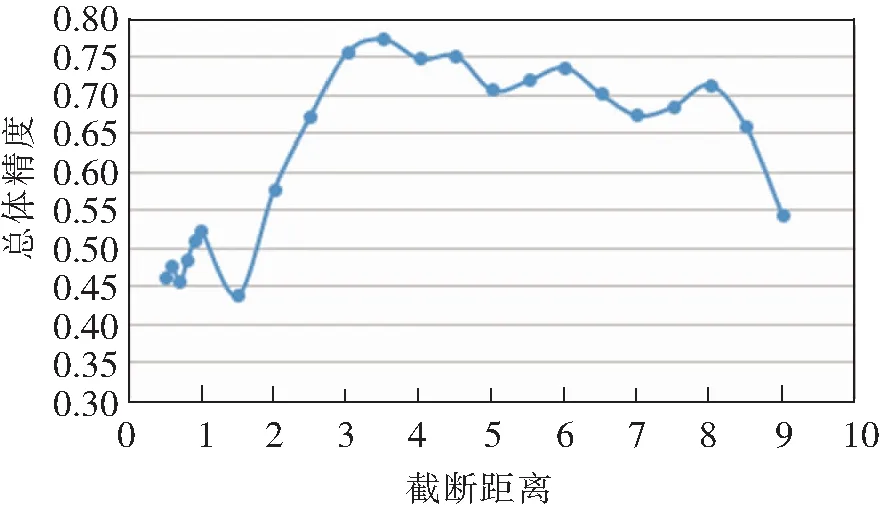
图8 截断距离与城市功能区分类总体精度关系图

3.4 功能区标注个数对分类精度的影响分析

本研究的目的是通过标记少量功能区的类型，获取更高的城市功能区分类精度。本文以北京市朝阳区为例，分析了采用本方法进行城市功能区分类时功能区标记个数对分类总体精度(计算方法同3.3)的影响，见图9。从图中可见，随着标记个数的增加，分类精度也在逐步提升。通常在有监督的机器学习算法中，会首先在总样本中至少选择50%的样本进行学习训练，然后采用训练好的模型进行分类。而采用本文所提出的方法对北京市朝阳区进行城市功能区分类时，标记的功能区个数达到50(占总功能区个数的6.75%)，分类精度达到一个较高的值。由此可证明本方法在节约标记成本的前提下，可取得较高的分类准确性。

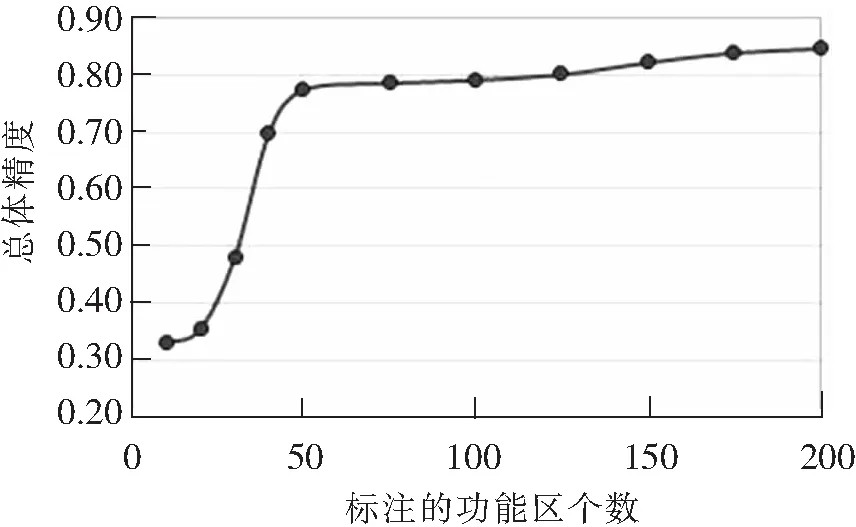
图9 标注的功能区个数与城市功能区分类总体精度关系图

4 结论

快速、准确地获取城市功能区空间结构不仅是城市规划管理者的需求，还可为人们日常生活、工作和交通等提供便利。然而，城市的快速发展导致了城市内部的复杂化与多样化，给城市功能区地图的获取带来了巨大挑战，近年来，城市功能区分类逐渐成为城市地理空间结构研究的重要问题。本文构建了一套城市功能区分类方法。一方面，该方法以POI为数据基础，数据具有较强的可获取性。另一方面，该方法基于主动学习算法实现，主动学习是一种半监督分类算法，可以少量标记为代价达到优于非监督分类方法准确性的效果。本文将该方法应用于北京市朝阳区的城市功能区分类，研究表明该方法具有较高的准确性。

本方法的准确性还可通过以下方面的改进得到进一步的提升：(1)指标体系的改进，指标体系是城市功能区分类的基础，根据分类结果的反馈，探究分类指标与功能区类型的相关性，改进与完善指标体系可进一步提高城市功能区分类的准确性；(2)数据源的扩充，仅使用POI数据使得本方法的数据源获取简单容易，但数据源的单一性同时也制约了本方法的准确性，如POI数据可反映地理实体的属性类别特征，但无法反映地理实体的功能强弱，若增加手机基站数据，以区域内的人流量表征区域功能的强弱便可弥补POI数据的不足。在后续的研究中将从以上两方面入手，以期进一步提升方法的准确性。