基于半球谐振腔的微光学加速度计结构设计仿真研究

张 婷, 杨 波

(1.东南大学 仪器科学与工程学院,江苏 南京 210096；2.东南大学 微惯性仪表与先进导航技术教育部重点实验室,江苏 南京 210096)

0 引 言

随着引力波的成功探测,激光干涉仪引力波探测器中的关键技术成为近年来的研究热点,其中光学谐振腔是其高精度探测能力的关键所在[1]。法布里—珀罗(Fbry-Pérot,F-P)腔是最为基本却非常重要的一种光学谐振腔,因其具有高灵敏度和低不确定性的特点,被广泛运用于各类传感器件。文献[2]提出了一种微纳集成的F-P腔光学加速度计,两个质量块连接着一个集成了分布式布拉格反射器的F-P微腔来实现低谐振频率和高效的光力信号变换。文献[3] 提出了一种基于光子晶体纳米微腔的加速度计,构造了一个用于检测质量块运动的“拉链式”F-P微腔,由输入加速度导致微腔的谐振波长变化,可以通过布置在固定侧光子晶体梁周围的光波导的倏逝波耦合效应测得。文献[4]提出了一种基于光纤F-P微腔的光力式加速度计,该传感器在熔融石英谐振器上集成F-P光纤谐振微腔,输入加速度使腔面的一端产生位移,导致谐振腔腔长发生改变,致使输出光谱变化。然而,传统的F-P腔存在光耦合稳定性差,有效精细度低,光学品质因数低等问题。

本文研究的基于半球谐振腔的微光学加速度计可以弥补这些缺陷,涂有高反射薄膜的半球腔具有更好的光学稳定性和高精细度,这将有利于进一步提高加速度和位移测量的准确性和精度。本文主要研究了反射膜、增透膜对于谐振腔测量结果的影响,以及基于半球谐振腔的微光学加速度计的输出信号解调方式。

1 传感器工作原理

基于半球谐振腔的微光学加速度计的总体结构如图1所示,由三部分组成,上层半球腔,中层硅微机械结构和下层玻璃基底。中层硅微机械机构受到外界加速度的作用,导致弹性悬臂梁变形,内部质量块将相对外部质量块产生垂直于结构平面的位移。上层半球腔面与中层结构内部质量块平面构成微纳半球谐振腔。微机械结构在外界加速度的作用下产生位移,导致半球谐振腔的腔长改变,进而引起谐振腔输出光强的变化。

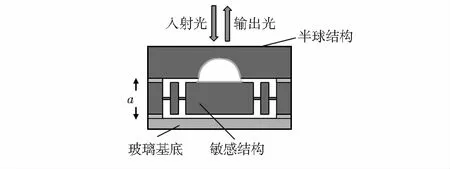
图1 加速度计总体结构示意

常见的谐振腔解调方式有强度解调法和波长解调法,一般针对单色光源采用强度解调法,对于宽光源,采用波长解调法。结合本方案设计特点,采用强度解调方式实现对输出光强信号的解调。系统采用单色激光光源,当输入光波长λ恒定时,由于外部加速度引起的半球谐振腔腔长的变化,将导致输出光强的改变,当谐振腔端面反射率较低时,输出光强与腔长的曲线近似正弦,在线性工作区,具有一一对应的关系[5]。在腔面镀上具有高反射率的反射薄膜后,线性工作区变短,将进一步提高谐振腔的精细度和品质因数。通过测得输出光强的变化就能得到腔长的变化值,进而得到外部输入加速度的大小。

2 半球腔的干涉原理

半球谐振腔是由平面腔改进得到,主要也是基于多光束干涉原理来检测被测量[6]。由两块平行平板构成一个光学反射腔,一束平行光以任意角度入射到腔内后,将在平板内部腔面间发生多次反射和透射并形成干涉。多光束干涉的原理如图2所示。

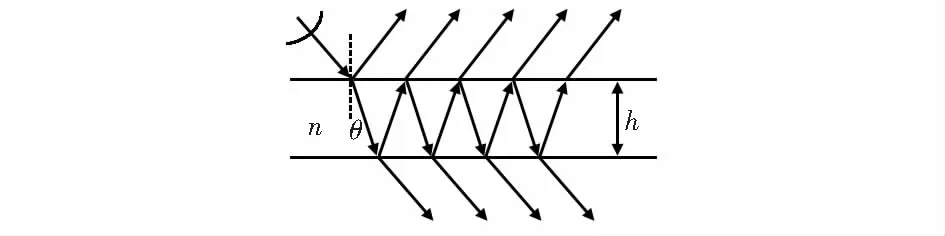
图2 多光束干涉原理示意

无论是反射光还是透射光,每束光和它前一束光之间具有固定的光程差和位相差。不考虑半波损失的情况下,几何光程差为

ΔL=2nhcosθ

(1)

位相差为

(2)

式中h为两光学平面间的距离,n为平面中间介质的折射率,θ为光线在两个光学平面内的倾角。

由于介质的不同,当光从光疏介质到光密介质界面发生反射时,其中电矢量的方向会发生突然的反向,导致振动相位的改变,此时需要在几何光程差ΔL上加上±λ/2,位相差也随之改变,引入了附加相位差π,可以表示为

(3)

假设入射光光强为I0,则反射光的光强可以表示为

(4)

透射光强为

(5)

式中R为两光学界面的反射率。

反射光强和透射光强呈互补关系,不同反射率下输出光强与相位之间的关系曲线如图3所示,极值位置和周期仅与相位差有关,与R无关。对于反射光强而言,输出最小值出现在δ=2kπ处,最大值出现在δ=(2k+1)π处,透射光强恰好相反。

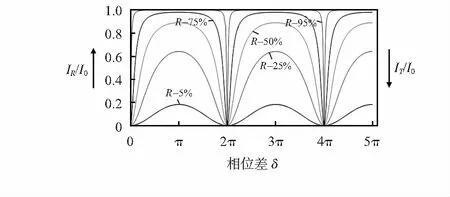
图3 不同反射率下输出光强与相位之间的关系曲线

3 关键特性研究

本文所研究的结构不同于光纤类F-P腔传感器,以光纤端面作为反射面而不用考虑反射膜、基底等因素的影响。本文以硅材料制作谐振腔,需要考虑硅材料对于光的透射能力以及光在硅腔面内的谐振效果。为了较好地实现光的传输和谐振,考虑在结构的输入平面添加增透膜,同时在谐振腔面内镀高反射膜。

3.1 反射膜

常用的反射膜有金属反射膜和全电介质反射膜。金属反射膜由单一金属构成,制备工艺简单,工作波长范围宽,由于具有较大的消光系数,可以使进入金属内部的光振幅迅速衰减,使得进入金属内的光能减少,而反射光能增大。消光系数越大,反射率越高；全电介质反射膜建立于多光束干涉的基础上,由不同材料的交替蒸镀而成,制作工艺较为繁琐,通过将各界面的反射光叠加,而得到较大的反射光能。考虑到工艺的加工难度,以及薄膜的稳定性等因素,在此选择金属反射膜作为谐振腔表面反射膜。

常用光学性质稳定的金属作为反射膜材料,包括铝、银、金、铜等。铝膜的高反射率波长区间很宽,是唯一一种从紫外到红外光谱区都具有较高反射率的金属材料,且极易被氧化成三氧化二铝(Al2O3),可对铝起到一定保护作用,应用广泛；银膜也具有很高的反射率,但其附着力较差,且易被硫化物氧化变色,应用较少；金膜在红外光区具有很高的反射率,与硅的附着性较好,不易被氧化,常用作红外反射镜[7]。本文采用的系统光源为1 550 nm的红外光源,且基底材料为硅,因此金膜为反射膜的首选材料。

金属反射膜反射率的高低也受其薄膜厚度的影响。当薄膜厚度小于自由电子的平均自由程时,其平均自由程随着膜厚的增大而增大,此时金属薄膜越厚,反射率越高；随着金属薄膜厚度的增加,当膜厚大于或者等于自由电子的平均自由程时,此时随着厚度的增加,反射率将保持不变[8]。

3.2 增透膜

本文所研究的结构采用硅材料制作,但硅的折射率很大,光直接照射在硅表面,无法被充分吸收,为了减少反射损失,考虑在入射平面表面添加一层增透膜,增大透射光能。

增透膜的选择需要考虑膜材料和膜厚度两方面因素。膜材料的选择与入射介质和透射介质的折射率有关。当入射角很小时,假设光从折射率为n1介质射向折射率为n2的介质,其介质表面反射率可以表示为[9]

(6)

假设空气、薄膜、硅基底的折射率分别为n1,n,n2,薄膜厚度为d,图4为光在单层膜中的反射示意图。

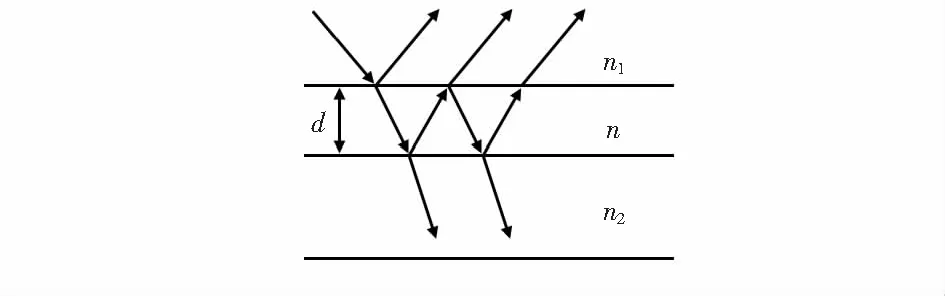
图4 光在单层膜中的反射示意

假设空气与薄膜之间的反射率为ρ1,薄膜与硅基底之间的反射率为ρ2,入射光光强设为1,一般只考虑前两束反射光线的光强。第一束反射光线经过空气直接由薄膜反射形成,其强度为ρ1；第二束反射光线经过两次空气与薄膜的折射和一次薄膜与硅的反射而形成,其强度为(1-ρ1)2ρ2。当两束反射光振幅相等且相位相反时,就可相互抵消,使得整个系统的反射能量几乎为零,则透射过去的能量大幅度增强。

要使前两束反射光线振幅相等,即要满足强度相等,则(1-ρ1)2ρ2=ρ1,代入式(6),经过化简得到薄膜的折射率应该满足

(7)

一般空气折射率n1为1,硅的折射率n2为3.42,则增透膜材料应该满足的折射率大约为1.85,Al2O3的折射率为1.76,是最为接近计算值的常用增透膜材料。

增透膜的厚度是影响膜透射效果的另一重要因素,要使上述两束反射光恰好反相,则需要两束光重合时,出现最大程度地干涉相消。由于两束光都存在半波损失,相互抵消,可以不予考虑。所以,当光从空气透过介质薄膜垂直射入硅基底时,前两束反射光的干涉情况与膜的厚度关系为

(8)

式中k为自然数,λ为光在介质薄膜中的波长。当膜的厚度d=(2k+1)λ/4,两束光线干涉相消,减弱了反射光的强度,增加了透射光的强度,让更多地光进入到谐振腔中。

4 仿真结果与分析

在选定好反射膜与增透膜的材料之后,利用时域有限差分(finite difference time domain,FDTD)光学仿真软件,依据加速度计的实际设计尺寸,搭建了仿真模型,如图5所示。利用仿真模型对反射膜和增透膜的厚度进行研究,同时,基于光强解调原理,实现了对输出光强信号的解调。

图5 加速度计仿真模型

4.1 反射膜厚度的影响

将系统光源设定为单色光源,波长为1 550 nm,腔长为250 μm,利用FDTD光学仿真软件对镀有不同厚度金反射膜的谐振腔进行仿真,得到单光源下的反射光强大小,结果如图6所示。

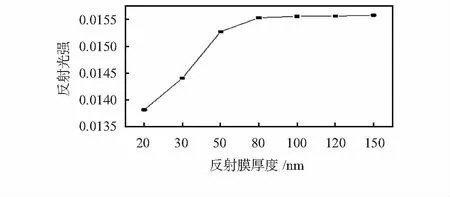
图6 不同厚度的反射膜与反射光强的关系

从仿真结果来看,反射膜厚度从20 nm逐渐增大到80 nm的过程中,反射光强逐渐增大,此时对应的金膜反射率是逐渐增大的,但光强值增大幅度并不明显,这是因为金本身在红外光区的反射率就已经在90 %以上[10],增加膜厚已经不能再显著增加其反射效果；当反射膜厚度大于80 nm之后,光强几乎不再变化,即反射率几乎不再改变。结合仿真结果和本文传感器的设计需求,选择厚度为30 nm的金膜作为谐振腔的反射膜。

4.2 增透膜厚度的影响

设定中心波长为1 550 nm,Al2O3的折射率为1.76,令k=0,由式(8)计算得到Al2O3增透膜的厚度为d=220.17 nm。

由于微纳加工工艺存在加工精度的限制,同时,谐振腔本身的结构尺寸、材料等因素,也可能导致实际的最佳增透膜厚度与计算结果有所差别,因此利用FDTD光学仿真软件对最佳增透膜厚度进行验证,设定系统光源波长为1 550 nm,腔长为250 μm,增透膜厚度区间为(210.17±20)nm,结果如图7所示。从仿真结果来看,当增透膜厚度为210.17 nm时,反射光强达到最大,这与实际计算的最佳厚度不同,误差在10 nm左右。同时,从仿真结果来看,在整个厚度区间内,反射光强虽然存在波动,但波动差值很小,这说明即使存在一些加工误差,对于反射光强的大小影响也不会很大。

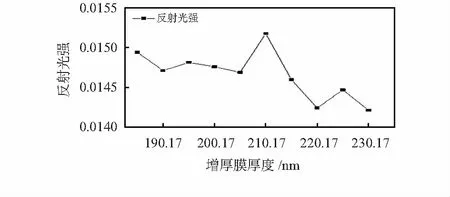
图7 不同厚度的增透膜与反射光强的关系

4.3 传感器仿真解调结果

设定半球腔的深度为190 μm,半球结构与中层结构键合厚度为50 μm,则整个谐振腔腔长为240 μm；增透膜材料采用Al2O3,厚度为220 nm；反射膜材料采用金,半球腔面膜厚度为30 nm,质量块平面膜厚度为200 nm。通过仿真得知,当金膜厚度为30 nm时,其反射率R1约为90.8 %,当金膜厚度为200 nm时,其反射率R2约为99 %。在不考虑损耗的情况下,谐振腔的反射率R可以表示为[11]

(9)

式中R1和R2分别为谐振腔两个端面的反射率,反射率R是相位差δ的余弦函数,随相位差δ呈周期性变化,且周期为2π。代入式(4),得到输出反射光强与相位之间的关系曲线如图8所示。

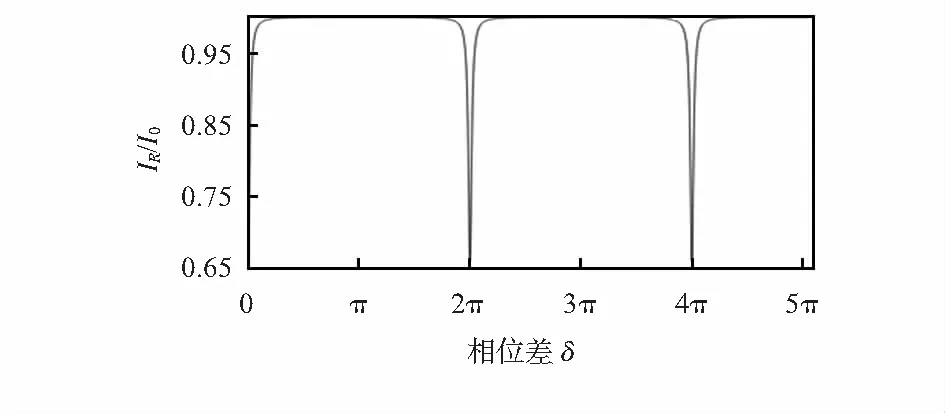
图8 输出光强与相位之间的关系

按照上述结构尺寸,通过FDTD软件进行光学仿真,得到半球谐振腔反射输出光强与不同腔长h的关系,仿真结果如表1和图9所示。当波长为1550 nm时,输出光强曲线的周期为λ/2=775 nm[11]。

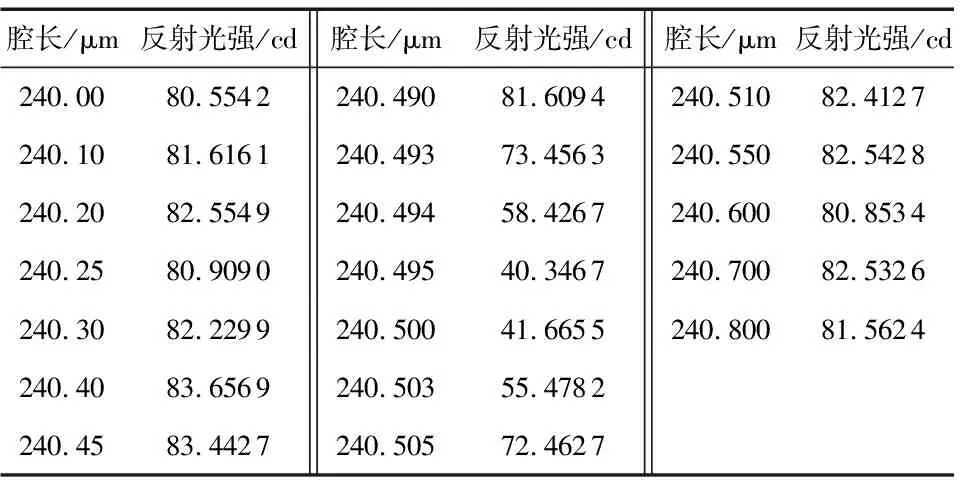
表1 反射输出光强大小与腔长的关系

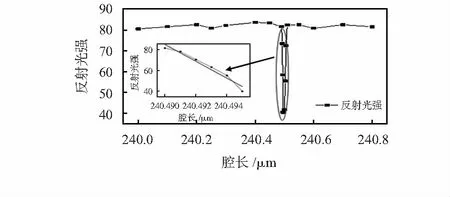
图9 基于半球腔的微光学加速度计解调结果

由仿真结果可知,线性工作区很窄,宽度为20 nm左右,波形陡峭,灵敏度为8.06 cd/nm。利用线性段光强信号与腔长变化量的关系可实现对微小位移量的敏感,进而实现对微弱加速度信号的敏感。

5 结 论

针对本文传感器结构,分析了反射膜和增透膜的材料选取对微纳腔特性影响规律,并利用FDTD光学仿真软件进行仿真测试,研究了不同膜厚对谐振腔谐振效果的影响。同时,基于光强解调原理,利用仿真软件得到光强信号与变化的腔长的关系,实现了对输出光强信号的解调,从仿真角度验证了本方案的可行性。后续会对设计完成的加速度计结构进行加工及测试,获得加速度计实际的灵敏度、动态范围等参数大小。