考虑B2C平台运作效率损失的多品采销协同优化研究

黄成忱 许茂增 崔利刚 刘孝林

(重庆交通大学 经济管理学院,重庆 400074)

0 引言

从平台型垂直电商到平台型综合电商,B2C电商平台(以下简称平台)推动着行业的发展与变革,同时也深刻地影响着网络零售商的运作活动[1-2]。天猫作为国内最大的B2C电商平台,2019年公布的最新DSR考核体系中,服务水平考核指标的权重增加;拼多多作为全球最大C2M拼团购电商平台,率先提出“5分钟回复率”服务指标;全球第一家B2C电商平台eBay,2019年也进一步更新了海外仓服务管理政策,规范了发货时效。随着行业生态链的完善,行业竞争加剧,为提高服务水平,降低平台运作效率损失,多商品联合采购及运营的策略被广泛应用于B2C电商行业。多品联合采购及线上运营的集成优化(Joint Replenishment Problem on E-Commerce with Operational Efficiency Loss,EJRP),是基于联合补货问题(Joint Replenishment Problem,JRP)的拓展研究,其将随机需求下的联合补货策略(Joint Replenishment Problem with Uncertain Demands,UJRP)应用于B2C网络零售行业,旨在通过分组协调不同商品的采购频次,更好地实现网络零售商的“采-存-销”协调运作,从而有效降低系统运作总成本。

而联合补货问题(JRP)始于对传统制造业库存协调优化的研究[3]。随着全球化生产的推进,竞争不再仅仅发生于孤立的实体之间,而往往发生于相互关联的企业或集团,甚至整个供应链之间[4]。更多的学者也将JRP拓展应用于供应链的协调运作领域,以库存控制为核心,着眼于供应链整体生产运作协调优化[5-6]。文献[7-8]研究了三级供应链下的联合采购策略,可见JRP通过结合更多具有现实意义的假设及集成供应链上下游相关操作,逐渐向供应链纵向集成优化方向拓展[9-10]。但相关研究仍聚焦于传统制造行业,近年,全球经济格局深度调整,推动着各个国家产业结构的优化升级,不少学者也开始关注JRP在更多行业领域的应用[11]。崔利刚等[12]针对一个配送中心-多个零售商的供应链结构,提出了结合多产品采购与配送的集成优化模型,其在快销行业具有较强的现实指导意义;而在农副、医药销售行业,产品的质量和数量易随采销进程的推进而变化,Qin等[13]针对新鲜农副产品,研究产品质量和数量随着时间同时下降情况下的多品联合定价与库存控制问题。然而,目前基于B2C电商领域的JRP研究较少,已有的相关研究中多假设第三方平台为免费服务提供方,忽略了平台对网络零售商实际运作的重要影响[14];部分研究从价格策略出发,基于收益共享契约,关注了平台对网络零售价格制定的影响[15],与之不同,EJRP则从操作层面出发,主要关注了平台运作效率对供应链整体运作成本的影响。

此类问题研究的另外一个瓶颈在于高效求解算法的设计[16]。JRP已被证明是一个 NP难题(Non-deterministic Polynomial Hard,NP-hard)[17],在模型求解上,主要通过启发式和元启发式算法[17-20],例如,RAND方法[21]、Power[22]和遗传算法(Genetic Algorithm,GA)[23-24]。启发式算法对于一些需要求解精确解的问题,在寻优速度和解的精确性上均有优势[25],但对于 JRP,一些元启发式算法则显得更具优势[26]。王林等人将差分进化算法(Differential Evolution Algorithm,DE)用于求解模糊结构的JRP模型[23]。该算法在JRP模型求解上表现出较好的鲁棒性和求解效率。但随着问题规模的增加,DE算法求解的精确性和鲁棒性随之减弱,更多的研究者尝试将智能算法引入求解[26]。BA算法(Bat Algorithm,BA)作为一种基于群体智能的算法,其受到蝙蝠回声定位行为的启发,把优化和搜索过程模拟成种群蝙蝠个体移动和搜寻猎物的过程[27],该算法最初主要用于解决(工程领域的)结构设计与优化问题。由于其具有实现简单、参数少等特点,该算法逐渐被应用于求解其他的领域的NP难题,如生产调度问题、优化选址问题、模式识别问题等[27],但在此类问题的求解上,BA表现出的鲁棒性并不理想。因此,本文提出一种两阶段的混合蝙蝠差分算法(BADE),这与一些混合算法不同[26],没有破坏算法固有的进化过程,将两个算法联合分别针对不同的决策变量类型进行粗搜索和细搜索,产生联合效应,一定程度上综合了两种算法的优势。

综合以上,本文主要研究工作与贡献为:(1)结合B2C运作实践,提出一个考虑平台运作效率损失的多品采购运作集成优化模型(EJRP),将“采-存-销”三个供应链的核心环节进行集成优化,从而有效降低系统总体运作成本;同时通过模型参数灵敏度分析,进一步获得更多有益的管理启示。(2)提出一种混合蝙蝠差分算法(BADE),通过与GA算法、BA算法、DE算法求解结果的对比分析,在兼顾求解性能的同时力求获得更具多样性的解方案;并考虑实际决策情景,在不同问题规模下进行了算法性能实验,拓展了算法的实用性。

1 问题描述及模型构建

基于经典的JRP研究,在B2C运营模式下,本文考虑了网络零售商通过第三方平台销售其产品的情景,其中,允许产品缺货,同时产品退货、平台惩罚会造成运营效率的损失,决策者综合其采购、库存、缺货、效率损失的情况进行决策。以上假设详细说明如下:①通过第三方网络销售平台出售产品,且愿意遵循平台运营规则;②顾客需求是随机的,并服从正态分布;③允许随机需求扰动而导致缺货的现象;④允许退货、平台惩罚带来的运营效率损失。模型参变量符号说明,详见表1。

表1 模型参变量说明Table 1 Notations description

1.1 多品联合采购模型(JRP)

经典的JRP模型主要研究的是确定需求下的多产品采购决策方案。需求假设相对简单,假设商品i年固定需求率为Di,各商品基础补货周期为T及商品i的联合补货频率为ki。单位时间内的单位库存成本为hi,则商品采购周期内对应的库存持有成本可表示为式(1):

相应的订购成本可表示为式(2),包含主要订购成本与次要订货成本,其中主要订货成本是指每次订货产生的固定成本,此项成本与联合订货的分组情况无关。而次要订货成本则考虑的是每次订货过程中的变动成本:

则经典JRP模型总成本为订购成本Co与库存成本Ch之

和,如式(3)所示:

1.2 随机需求的多品采购模型(UJRP)

在移动互联网技术的助推之下,如今的B2C运营环境更加复杂多变,顾客需求呈现出碎片化、随机化的态势。UJRP基于经典的JRP模型引入随机需求的假设。由于需求的不确定性,UJRP增加考虑了缺货成本Cs。这里假设产品需求独立同分布,且服从高斯分布,则观测周期内的最大库存水平Ri可表示为Ri=Di(kiT+Li)+ziδi(kiT+Li)。 其对应的库存持有成本可表示如下式(4):

基于以上假设,缺货成本可表示如式(5),其中E(xi-Ri)+为超出最大库存水平部分的产品需求期望,f(zi)、F(zi)分别表示其对应 的概率密度函数(PDF)、累积分布函数(CDF)。

则考虑随机需求的UJRP模型总成本包含订购成本、库存持有成本、缺货成本,可用式TC=Co+Ch+Cs表示。

1.3 多品采销协同优化模型(EJRP)

EJRP模型在UJRP模型基础上,考虑了第三方平台对于网络零售商运营的影响,将采购成本Co、库存成本Ch、缺货成本Cs及平台运作效率损失Cl集成优化。其中采购成本如下式(2),由固定采购成本和变动采购成本组成。结合实际运营,模型考虑了商品退货,退货率为ri,此时,商品i的库存水平可表示如下式(6):

其最大库存水平及对应库存持有成本分别可表示为式(7)、式(8),同时考虑了安全库存因子zi对其的影响:

此外,运营损失成本主要考虑的是延时服务造成的平台惩罚成本及退货造成物流损失成本。由式(9)表示,其中E(xi,kiT+Li)γi、E(xi,kiT+Li)ri分别表示延时发货产品期望及退货产品期望。

则EJRP模型总成本为采购成本、库存持有成本、缺货成本及(平台)运作效率损失成本之和,如式(10)所示:

2 模型求解与算法设计

BA算法作为一种基于群体智能的算法,其受到蝙蝠回声定位行为的启发,把优化和搜索过程模拟成种群蝙蝠个体移动和搜寻猎物的过程[12]。DE算法是一种基于群体差异的启发式随机搜索算法,其在求解此类问题上具有良好的鲁棒性,故被广泛应用于此类问题的求解。而BADE算法则综合了BA的全局寻优能力和DE的鲁棒性的优势,形成一个两阶段的混合算法。第一阶段,利用BA进行粗搜,生成当前最优蝙蝠位置及其相应的适应度值,然后输出作为DE的初始输入。在第二阶段,DE起主导作用,针对离散型变量进行优化。因此,BADE基本保留了BA和DE两种算法的优越搜索机制,具有较好的求解性能,且在不同问题规模求解实验中,表现出较BA、DE算法更优的准确性和鲁棒性。对于EJRP模型,我们以最小总成本为目标函数值,求解时以此目标函数值为适应度函数值。详细求解流程如图1所示,其中主要包括以下五个核心求解步骤:

图1 BADE两阶段求解流程图Figure 1 The two stage solution flow chart of BADE

步骤1初始化

本文主要采用均匀分布的方式进行种群的初始化。初始化完成后即进入BADE求解的第一阶段,这一阶段主要目的是利用BA求解的原理进行粗搜。

步骤2蝙蝠粗搜

将步骤一中获得的初始染色体向量作为当前蝙蝠的初始位置向量,根据式(11)-式(13)的策略进行全局寻优。等式(11)-(13)分别表示第i个蝙蝠的频率、速度及位置。速度和位置在每次迭代后会更新,而频率是影响更新步长的一个因素。假设,β是一个随机值,且有β∈[0,1],式(12)中x*表示当前时刻的全局最优值。

在前最优位置向量x*附近再进行一次局部搜索,利用式(14)针对连续型变量进行优化,同时利用式(15)、式(16)获取蝙蝠位置变化后的响度和脉冲率。当蝙蝠接近猎物时,响度的值减小,脉冲发射率增加,其中α和η是常数。简单起见,α和η可以被认为是相等的[27]。 粗搜完成后即进入BADE算法的第二阶段,这一阶段主要目的是针对离散型变量进行进一步搜索优化。

步骤3差分变异

将步骤二获取的蝙蝠位置向量集作为DE种群进行变异操作,具体变异策略如式(17),其中pbesti,j(t)为当前最优的染色体,F为预设的变异算子,vij(t+1)为突变后的染色体。式(17)的变异策略可以保证基因突变的方向更贴近当前最优染色体,提升了算法寻优效率。

步骤4交叉重组

在交叉重组这一步骤中,对每一个维度,参照式(18)构造新染色体,其中Cr为交叉概率值。

步骤5比较选择

根据贪婪选择规则进行选择操作,如式(19),计算每个染色体的适应度值fitness(Xi(t)),如果后代染色体的适应度值小于父代,即有fitness(Xi(t+1))＜fitness(Xi(t)),则父代染色体被子代染色体更新替换;同时输出当前最优的适应度值pbest(局部最优值),如果当前pbest小于历史最优的染色体的适应度值gbest(全局最优值),即有pbest＜gbest,则更新历史最优的适应度值。

3 算例及敏感性分析

在这一部分,本文以一个包含6产品项的案例,分别针对JRP、UJRP、EJRP模型求解,考虑到GA算法也是求解此类问题较为常用的方法之一[8,17,28],故同时选取 GA、DE、BA三种算法与BADE算法进行对比分析。首先,从最优成本值、(最优成本出现的)频次、成本方差值、平均成本值等指标进行了计算结果的对比分析。此外,通过解方案中产品采购频次ki值的对比,考查了解方案的多样性。其次,通过模型参数灵敏度分析,讨论了输入参数扰动对最优成本的影响。最后,结合实际应用场景,在不同问题规模下进行了算法性能的进一步验证。以上算法均在Matlab®R2017a中编码,实验在一台装Windows®7旗舰版操作系统的个人计算机上运行(计算机CUP参数如:Intel(R)Core(TM)i7-4600U CPU;2.1 GHz、8 GB RAM)。

3.1 算例分析

针对6产品项的JRP模型,参考前人研究[8,17,24]与真实案例数据设置了实验初始数据,详见表2。基于初始参数数据的初步试算,我们可以进一步确定决策变量ki和zi的搜索空间。其中,ki代表商品i基于采购周期的联合补货频率,文献[17]将ki设置为[1,5],结合网络零售行业的交易特征,联合补货过程涉及更加丰富的产品品类[18],补货频率ki的取值范围也应更广,故这里将ki的搜索空间设置为[1,8]。考虑到T的观测时间超过一年,因此其搜索空间预设为(0,1);同时结合王林等人的研究[24],将安全库存系数zi的搜索空间设置为(0,3]。

表2 问题参数数据表Table 2 The problem parameters for experiments

针对 JRP、UJRP、EJRP 模型,同样运用 GA、BA、DE 作为比较算法求解三个模型,重复运行50次,四种算法的计算结果展示如表3,其中频次代表最优成本值在50次运行结果中出现的频次。当目标函数值与最优成本值之间的差值小于0.001,即|TCi-min(TC)≤0.001|时,则假定其值与最优成本值相等,频次增加计数1次。表3中结果表明,在求解JRP模型中,四种算法相较而言,DE、BADE两种算法鲁棒性都比较好,但DE算法方差最小,最优值出现频次最高,表现突出。而在求解UJRP、EJRP模型时,GA、BA两种算法鲁棒性(较求解JRP模型而言)明显减弱,但DE、BADE两种算法仍然表现出较好的稳定性。值得注意的是,在求解EJRP模型时,BADE算法求解方差最小,最优频次最高,鲁棒性优势明显。从最优值搜索情况而言,GA算法在三个模型求解时,均出现早熟的情况,搜索性能最差;而BA算法只有求解JRP模型,求解出的最优值与DE、BADE算法相近,在后两种模型中均出现早熟;针对EJRP,BADE算法求解最优值情况最佳。综合可见,BADE算法对于EJRP模型具有较好的求解潜力。

表3 求解结果对比Table 3 The com parison of com putational results for JRPs

对于管理者而言,在不确定性较高的B2C环境下,算法求解出的可行方案的多样性,在管理实践中也尤为重要。以上主要从最优成本(目标函数值)求解情况来评价几种算法的鲁棒性与寻优化能力,接下来我们通过考察可行方案中产品补货频次(即决策变量ki)的多样性,进一步对比分析算法求解的多样性。基于前文算法鲁棒性与寻优能力上的评价结果,这里重点选取BADE与DE两种算法进行对比分析。以6产品项情景为例,随机选取求解过程中,最优成本函数值在误差范围内的50组可行方案,图2(a)(b)(c)分别是表示JRP、UJRP、EJRP三种模型解方案多样性的对比结果,即对应可行方案中ki(产品补货频次)可取值的散点图。ki可取值越多,图中点位波动越频繁,一定程度反应了解方案的多样性。

图2 解方案多样性对比Figure 2 The diversity com parison of solutions

图2(a)中左、右两边分别为BADE算法、DE算法ki值波动情况,左右对比可见,BADE所得方案中(以下统称“前者”)k3、k4、k5、k6均具波动性,而 DE 算法所得方案中(以下统称“后者”),仅有k3、k5、k6具有一定波动性。其中后者k3、k5、k6的波动频次也明显少于前者。同理可见,图2(b)中,后者仅有k6具有波动性,前者则是k3、k4、k5、k6均具波动性,且k6的波动(可取值)范围更广。而由图2(c)可见,两者求解该模型得出的可行方案中,ki的波动情况会较前两种模型更少,但仍然有前者ki的总体波动频次更多。 综合可见,前者即BADE算法求解三种模型而言,多样性较DE更佳。

为进一步呈现算法优化迭代过程,本文随机选择了EJRP上的4种算法的搜索过程,如图3所示,最大迭代100代,每种算法重复运行50次。迭代过程中,BADE算法在28代时开始收敛,而DE算法、BA算法分别从第50代和第85代开始收敛;而GA算法虽从第76代开始收敛,但出现了早熟现象。另外,从算法准确性来看,BADE和DE算法所求的总成本函数值较为接近,从图3的中的局部放大图,可见,BADE算法所求最优成本值小于DE算法,且在四种算法中最优。

图3 算法优化过程对比Figure 3 The com parison of optim ization process for GA、BA、DE and BADE

3.2 敏感性分析

在充分证明BADE算法性能的基础上,我们进一步展开模型问题参数的灵敏度分析,考察看模型输入参数扰动对模型目标函数值(最佳总成本值)的影响。图4(a)(b)(c)分别展示了JRP模型、UJRP模型及EJRP模型中,随着不同的问题参数变化,总成本函数值总体的变化的趋势。其中,参数变化范围为-80%至80%,变化步长为20%,分析时采用每种算法运行50次获得的总成本平均值。综合分析,可见JRP模型成本变化率波动范围大于UJRP和EJRP,意味着在构建JRP模型时,其涉及的成本诱导因素越多,则它们对成本费用总体影响就越大。具体地,对JRP模型而言,年需求量Di和持有成本hi是最具影响力的参数,但在UJRP模型中,由于需求的不确定性,最具影响力的参数转变为持有成本hi和需求方差δi。 但在EJRP模型中,商家依托于第三方电商平台,在考虑平台运营效率的影响下,年度需量的影响相对其他参数的影响更为明显,从管理者角度而言,这一定程度上体现出依托第三方平台的网络零售运营模式在抵抗需求波动上的确具有一定的优势;除此之外,不容忽视的是退货率指标对总成的扰动接近30%,可见在网络零售环境下,尽可能地提升服务水平,降低退换率,对于系统总成本优化极具现实意义。

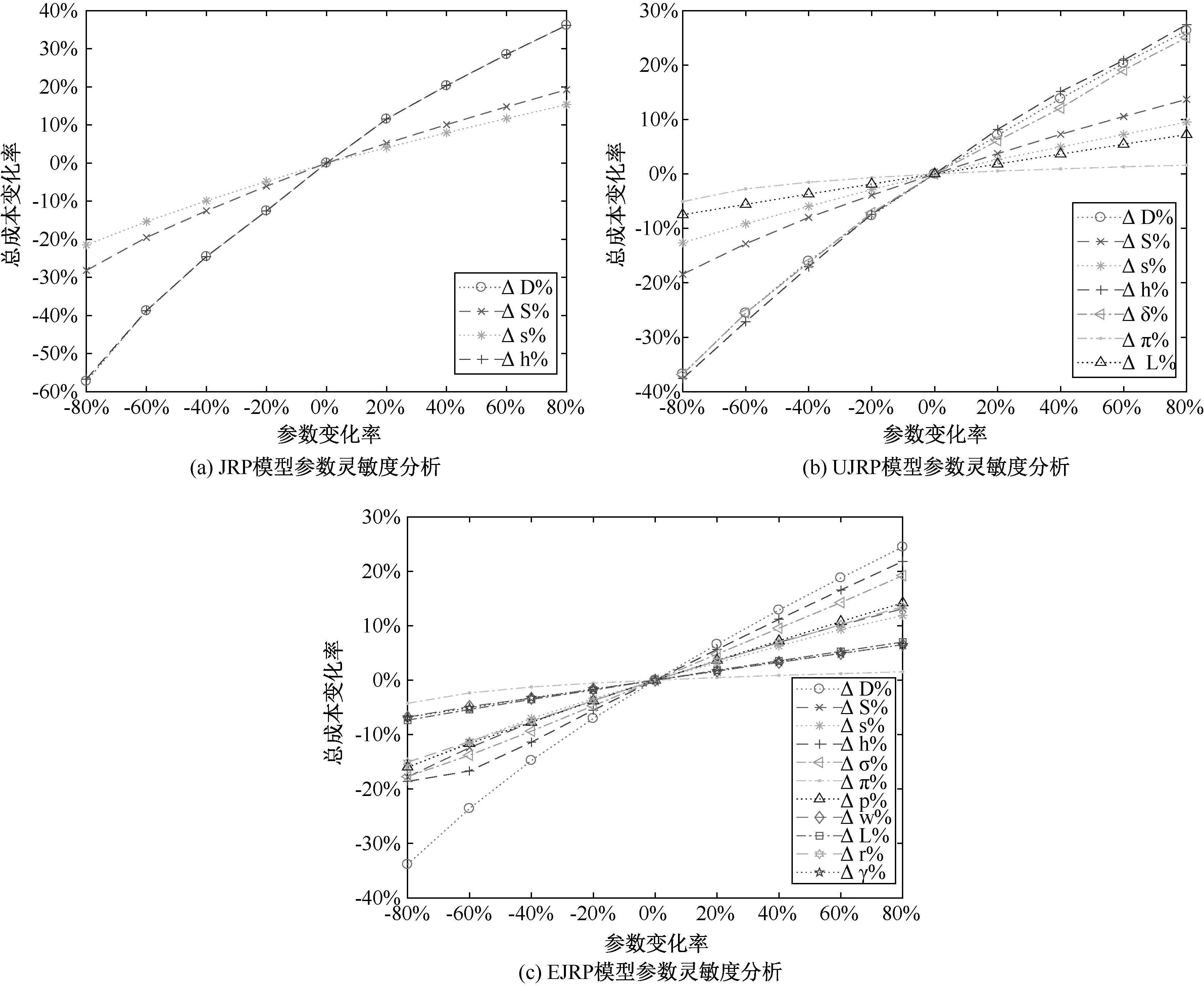
图4 问题参数灵敏度分析Figure 4 The sensitivity analysis of problem parameters

3.3 问题规模分析

在拓展实验中,我们将产品规模扩大,进一步测试了在更一般的情境下,BADE算法求解EJRP模型的性能,这一点在算法的实际应用中尤为重要。其中仅选择在前面实验中表现出较好求解性能的BA、DE算法与BADE算法进行对比,所有算法均重复运行50次,并以50次运行结果中的最优总成本、成本平均值、成本标准差及平均搜索时间为统计指标进行分析。表4为实验输出结果,以上结果主要表明:(1)产品规模较小时,BADE算法和DE算法搜索性能,综合寻优能力和鲁棒性两者性能相当。例如产品项为10、12、15时,问题规模较小,不难看出两种算法的最优成本、平均成本及方差等指标的数值相近,但BADE算法求解所得的标准差指标值略小,显示出更好的稳定性。(2)随着问题规模的增加,BADE算法的寻优能力愈加突显。具体地,产品项从24到96时,就最优成本、标准差两项指标值而言,BADE与另两种算法对应指标值的差距较大,例如当产品项为96时,BADE求解的最优成本值较BA、DE而言分别降低约46%、5%,说明该算法在较大问题规模情境下具有较好的求解潜力。但通过求解时间指标值的对比,DE求解效率略高,尤其针对中小问题规模。综上分析,BADE求解多样性更好,故在问题规模较大时,算法潜力更大;但由于该算法分为两阶段求解,故在求解速率上,特别是问题规模较小时,较DE算法没有明显优势,但仍然优于 BA算法。

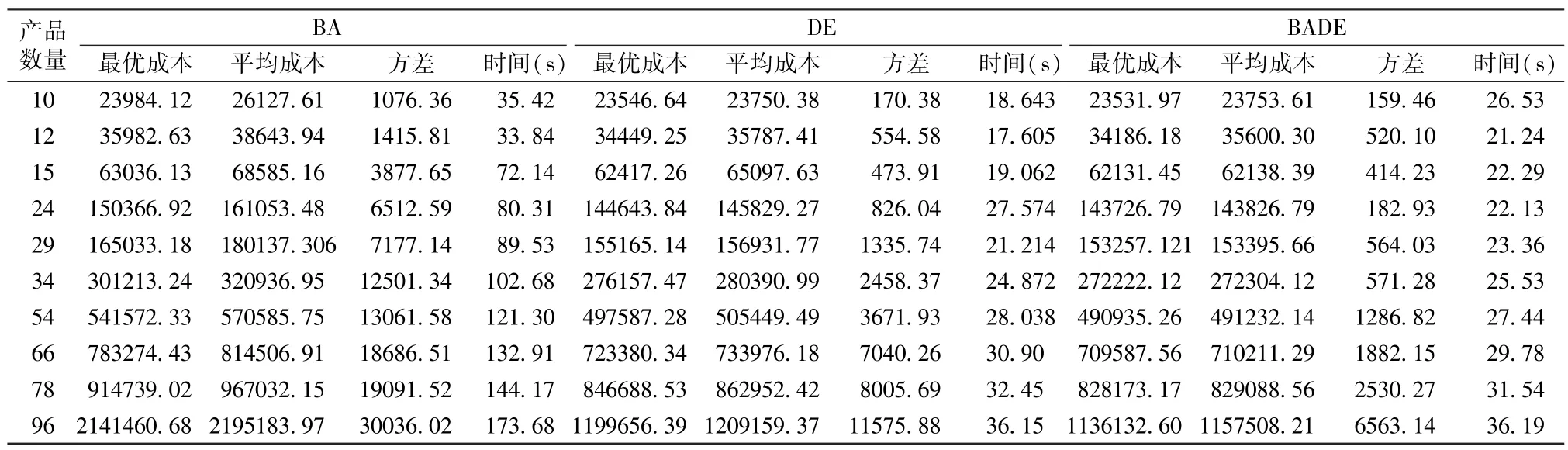
表4 不同问题规模的EJRP结果对比Table 4 Com putational results of BA,DE and BADE under various-scale EJRPs.

4 结论

本文在B2C运营模式下,基于经典的多品联合采购问题(JRP),针对网络零售商提出一个考虑平台运作效率损失的多品采销协同优化模型(EJRP),着眼于网络零售商供应链的核心环节,进行“采-存-销”系统总成本优化。本文通过JRP模型、UJRP模型、EJRP模型参数灵敏度对比分析发现:(1)对比UJRP模型、EJRP模型,前者需求波动对总成本的影响大于后者,这一定程度上体现出依托第三方平台的B2C运营模式在抵抗需求波动上具有一定的优势;(2)在EJRP模型中,退货率、延时服务率等影响运作效率的指标对总成本的扰动较大,不难看出在同质化竞争激烈的网络零售环境,提高平台运作效率,加强相关指标的控制与管理愈显重要。

同时,本文设计了一种混合蝙蝠差分算法(BADE),分别针对决策变量的不同类型,利用BA、DE算法协同寻优。本文通过与GA、BA、DE几种算法的对比分析(分别求解JRP、UJRP、EJRP),主要得出以下实验结果:(1)求解的问题规模较小时,DE算法的鲁棒性较好,但随着问题规模的增加,BADE算法的鲁棒性优势逐渐显现;(2)尽管针对经典的JRP模型求解时,BA、DE、BADE几种算法求解性能差距相对较小,但针对UJRP、EJRP模型时,BADE均展示出较好解的多样性,以往研究中,较多的算法设计者仅关注了算法的鲁棒性和准确性,但在实际管理决策环境中(尤其在多变的网络零售环境之下),多样的可行方案,利于提供给决策者合理的决策空间,一定程度地拓展了模型的适应性。

后续研究中,我们将围绕本文提出的EJRP模型,针对网络零售商分阶段补货的情景,研究分析多阶段的EJRP模型,进一步优化BADE算法流程以满足多阶段EJRP模型求解的需求。同时增加算法自适应控制变量,进而优化算法大规模问题求解的效率。