基于超声驻波场的水下颗粒操控研究
张 洁,刘春泽,王 欢,许小芳,周红生
(1. 中国科学院声学研究所东海研究站,上海 201815;2. 中国科学院大学,北京 100049)
0 引 言
超声操控技术是对微小物体进行非接触操控的一种新型重要手段[1]。在生物医学领域,该技术可用于靶向给药的治疗方式[2],将药物载体通过超声场操控移动到指定病灶部位后释放,实现高效、无创、精准治疗。其原理是利用高强、高频声波的非线性效应产生声辐射力来实现对微粒的捕获和操控[3]。当一束声波入射到物体表面时,物体会对声波产生散射、折射和吸收作用,与声波发生能量和动量的交换,导致物体受到一个不为0的平均压力,称为声辐射力[4-5]。相比较光学、电场和磁场操控技术,超声操控具有明显的优势,能够以更具生物相容性的方式操控更多的材料[6-7],拥有广阔的应用前景。
Gor’kov[8]将物体表面的声辐射力表示为物体表面动量通量的时间平均,推导出微小球形物体在任意声场中势能的解析解,依据声场分布便可确定该物体的声势能,而声辐射力大小与声势能梯度有关,方向指向声势能极小值处,故而可以构造特定声场将物体限制在指定的空间位置。驻波产生的声辐射压力远大于行波,所以常用驻波场完成颗粒束缚。Park等[9]、Hong等[10]和Xic等[11]基于该理论设计了多种利用驻波声场的操控装置,分别实现了在空气中对固体颗粒、液滴以及昆虫(活体生物)的悬浮。Wu[12]和 Hcrtz[13]推导了球形颗粒在驻波声场受到的声辐射力的解析式,并且在液体环境下通过两个聚焦超声换能器完成了对微米级物体的捕获实验。
但是以上理论及模型均忽略了传播介质的热黏性作用,并且实际上对颗粒的操控不仅仅依靠声辐射力,也受到由声流场产生的曳力的影响。这里的声流场也是声波的非线性效应产生的,它是由介质的黏性衰减导致声场的空间梯度发生变化,介质振元的净位移不为零引起的全局流动[14-15]。文献[16-17]在现有理论的基础上利用无粘声波散射理论的远场解表示粒子上的辐射力,将此解扩展到靠近粒子的近场区域,然后将其与粒子声边界层中不可压缩的黏性流动问题的解进行匹配,重新推导了黏性流体中的声辐射力公式。
本文基于 Bruus的粘性介质中的声辐射力理论,建立了超声驻波场驱动下的水下颗粒操控模型,利用物理场仿真软件对模型中的声场、声流场进行仿真,分析颗粒小球受到的声辐射力及声流场引起的Stokc曳力大小,以及两种作用力的相对关系,动态模拟颗粒小球操控过程。最后设计对不同尺寸颗粒小球的水下驻波场操控实验,验证了颗粒操控的可行性以及声流场对颗粒操控会产生一定的影响。
1 黏性介质声辐射力理论


2 计算机仿真
本文采用基于有限元方法的多物理场仿真软件COMSOL Multiphysics进行声场、声流场和颗粒操控动态过程的仿真,模型的具体仿真参数如表1所示[20]。

表1 计算机仿真的模型参数Table 1 Model parameters of computer simulation
水下颗粒操控系统采用三维建模,模型示意图如图1所示,图中灰色区域是高为20 mm,半径为10 mm的圆柱体水域,紫色为两个凹球面超声聚焦换能器,孔径半径为 4.53 mm,曲率半径(焦距)为10 mm。除换能器表面外其他壁面贴附吸声材料,在仿真中将边界设置完美匹配层,表示无声波反射。设定发射超声的频率为1 MHz,红色箭头为换能器声场辐射方向。以下方换能器孔径平面中心为原点O,通过原点O在孔径平面内任选两条垂直轴线定为x轴和y轴,上下换能器中心点的连接线为z轴,建立三维直角坐标系。

图1 水下颗粒操控系统示意图(单位:mm)Fig.1 Schematic diagram of underwater particle control system (unit: mm)
2.1 声场仿真
声场仿真采用热黏性声学模块进行建模,两个换能器孔径平面的中心间距为20 mm,将换能器的曲面设置为速度振动条件,通过调整速度幅值可以改变声场声压值的大小,振动方向与曲面切线垂直,向空间辐射连续正弦声波。计算得到稳态声场的声压如图2所示。由于声波的干涉效应,在三维声场中z轴线上聚焦并形成局部驻波声场,声场内最大声压值0.295 MPa,其中图2(a)为三维声场声压图,图2(b)为xOz切平面的声压图。

图2 聚焦声场声压图Fig.2 Focused acoustic pressure diagram
2.2 声流场仿真
将上文计算得到的稳态声场作为源场,利用层流模块对Navicr-Stokcs方程的时均二阶扰动方程进行求解,在模型中添加体积力和质量源,最终得到时均二阶速度场v2即所谓的声流速度场。为减少计算机运算量且该三维模型具有轴对称性,故采用xOz切平面声场解进行流场仿真。设定初始条件为域内流体速度为0,根据式(3)~(4)计算得到的稳态流场如图3(a)所示,图中背景为流速大小,白线为流线,与线上箭头共同表示流动方向,静态水域在声辐射力的作用下从两个换能器辐射表面开始加速,并在中心位置汇聚减速,随后向左右两侧进行分流,碰到两侧的壁后形成回流。图3(b)为z轴上的流速值,以轴线中点为中心镜像对称分布,轴线上最大流速为0.09 mm·s-1。

图3 稳态声流场仿真结果Fig.3 Simulation results of steady acoustic flow field
2.3 颗粒操控仿真
操控的颗粒小球采用密度和水接近的聚苯乙烯材料,仿真中忽略颗粒重力和浮力影响,同时忽略颗粒之间的相互作用,使其仅受到声辐射力和声流曳力的作用,在声场和流场稳态解的基础上,采用粒子追踪模块与瞬态研究,根据式(5)~(6)添加声辐射力与声流曳力,初始时刻将小球均匀分布在xOz切平面声场内,计算6 s中的小球运动变化轨迹。
图4为颗粒聚集动态过程图,选取了以坐标(-1.5 mm, 8.6 mm)、(-1.5 mm, 11.4 mm)、(1.5 mm,8.6 mm)和(1.5 mm, 11.4 mm)为顶点的局部驻波场区域进行展示,背景为式(8)计算的该区域内时间平均势能Urad。0 时刻颗粒小球均匀分布在平面内,在合力的作用下发生移动,颗粒集群运动趋势为快速的纵向聚集,然后以相对缓慢的速度完成横向聚集,最终在6 s时达到稳定状态,聚集在Urad极小值附近。移动过程中,初始位置距离势能最低点最远,即处于驻波场波峰或波谷位置的颗粒,获得最大速度可达到 0.028 m·s-1,但该位置并不是获得最大初始加速度的位置,下文予以说明。

图4 颗粒聚集动态过程Fig.4 Dynamic process of particles aggregation
3 仿真结果分析
在颗粒聚集动态图中,取图4中第6 s图中的结果作为颗粒操控的稳态结果,选取z轴数据,画出该轴线上的声压、辐射力和时间平均势的曲线,并进行归一化处理,结果如图5所示。图5中红点标记处为颗粒聚集点,该点位于驻波场声波波节位置。从受力角度分析,声辐射力曲线的正负代表力的方向,该聚焦点正处于声辐射力的正值变化为负值的临界点处;从势能角度分析,该点对应于平均时间势能曲线的最小值,与时间平均势理论相符合。颗粒在声辐射力极值点处获得最大初始加速度,该位置对应于驻波场中波节与波峰(或波谷)的中心处,如图5中蓝点位置。
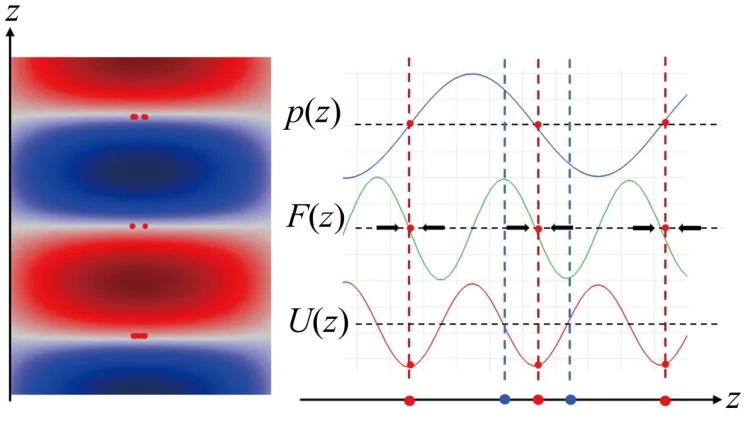
图5 z轴线声压、辐射力和时间平均势的归一化曲线Fig.5 Normalized curves of sound pressure, radiation force and time average potential alongz-axis
3.1 作用力分析
在xOz平面内的驻波声场中,声辐射力的方向并不完全与声传播方向(z轴)平行,可以分解到z与x两个方向,分别称为纵向声辐射力与横向声辐射力。图6选取了z轴上1/2波长宽度的声场绘制了声压和声辐射力图。图6中绿色箭头代表声辐射力,箭头的方向代表箭头中心位置处声辐射力的方向,箭头的长度与声辐射力的大小成正比。
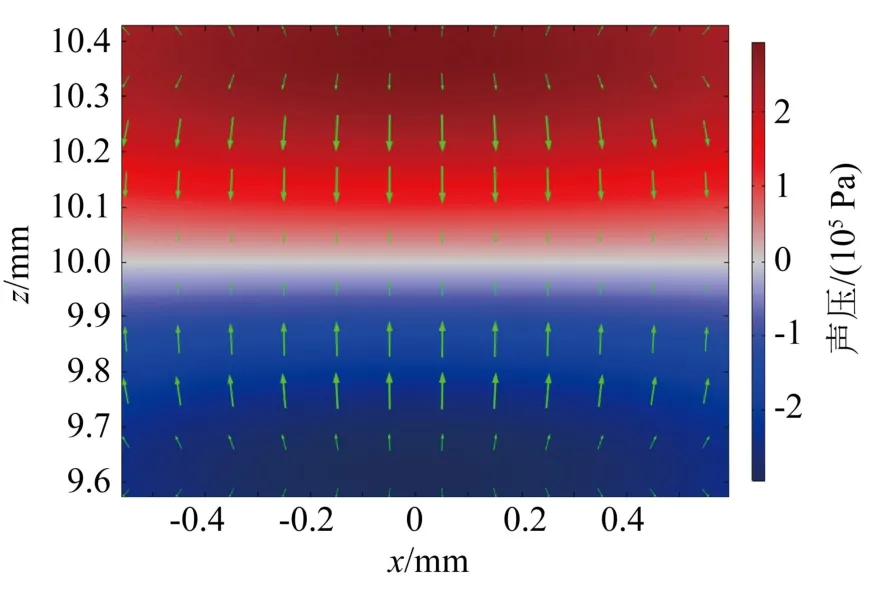
图6 1/2波长区域内的声压和声辐射力图Fig.6 Sound pressure and radiation force map in the 1/2 wavelength region
图7为纵、横声辐射力图,由于纵、横声辐射力数值分布差别较大,所以对箭头长度进行归一化处理,绿色箭头仅表示力的方向,图7(a)、7(b)两图解释了颗粒小球在纵向声辐射力的推动下向着波节位置移动,并在横向声辐射力作用下向着z轴进行靠拢,完成颗粒聚集过程。

图7 1/2波长区域内的声压和声辐射力图(分解后)Fig.7 Sound pressure and radiation force map in the 1/2 wavelength region after decomposition
接下来对作用力进行具体的数值分析,添加了颗粒静止状态(u=0)时的声流曳力,同样将其分解到z与x方向,称为纵向曳力与横向曳力。选取z轴和同x轴平行且z=10 mm的轴线上绘制一维作用力图,力场分析结果如图8所示。蓝线为声辐射力曲线,绿线为声流曳力曲线,图8(a)为纵向作用力曲线,最大声辐射力为 3.6×10-8N,最大曳力为1.07×10-10N,右下角为曳力放大后的波形图,前者约为后者数值的300倍,因此在纵向上声辐射力作为颗粒控制的主导作用力,将颗粒束缚在驻波的每一个波节处。图8(b)为横向的作用力曲线,最大声辐射力为7.51×10-10N,约为纵向声辐射力的1/50,最大曳力为3.9×10-11N,在该方向上两个力的大小相对差值较小,颗粒的操控力由两个力的合力决定。总之,粒子在驻波场内受到的纵向作用力要远大于横向作用力,故而图4中颗粒会在极短时间内沿着纵向聚集,然后缓慢在横向进行移动,最终汇聚为一团。

图8 纵、横方向上的作用力曲线图Fig.8 Action force curves in the vertical and horizontal directions
3.2 颗粒小球半径对操控的影响
颗粒小球在水中的操控过程,可以认为是其受到的声辐射力与曳力的“博弈”。根据式(5)、(6)可知,颗粒小球受到的声辐射力和声流曳力分别与颗粒半径rP3和rP成正比。利用超声驻波场束缚颗粒通常要求物体尺寸小于1/3~1/4波长[21],为研究颗粒小球半径对操控的影响,设置半径为 74、37、18和10 μm,计算横纵轴线上的作用力,分析两种力的关系,结果如图9所示。


图9 不同颗粒半径下的横纵向作用力的曲线图Fig.9 Curves of transverse and longitudinal forces under different particle radii
图9中蓝色虚线表示声辐射力,绿色虚线表示声流曳力,红色实线代表颗粒小球受到的合力,其中作用力值的正负代表力的方向,合力值为0的点表示该位置处声辐射力与曳力平衡,即为颗粒小球的束缚点。图9(a)中绿线幅值较蓝线小很多,绿红两线基本重合,表明合力与声辐射力相近,此时颗粒小球主要靠声辐射力进行操控。图9(b)、9(c)表示随着颗粒尺寸的减小,声辐射力与曳力的差值也在逐渐减小,合力发生了一些变化,此时合力的零值点有三处,一处位于中心,两处分别偏离中心约1.5mm位置,其他区域内颗粒随着声流被推出驻波声场。最后当颗粒半径减小到10 μm时,如图9(d)所示,仅有中心一处合力的零值点,此时颗粒放置在该平衡位置外的其他区域内,均由声流曳力控制其移动。图9(c)、图9(f)分别为纵轴上半径 74和10 μm颗粒受到的作用力,相比较横向合力的变化,半径减小到10 μm时仍以声辐射力为主要作用力,但是此时由于横向作用力以曳力为主,颗粒小球会随着声流运动,无法形成团聚。
3.3 声场强度对操控的影响
有研究表明随着声场强度持续增加,声流场从层流过渡到湍流时,流场分布会发生变化且更加复杂[22],所以本文研究的声流场仅处于层流的范围内。
改变阵面的振速幅值可以调整声场强度,令声场最大声压值分别为0.074、0.147和0.295 MPa,大小比例为1:2:4,计算得到三种不同强度的声场对应的声辐射力比值为 1:4:16,声流曳力比值同为1:4:16。在式(5)、(6)忽略式中系数,主要变量为,由于振速与声压存在关系:,p1和v1是声压和振速一阶量,v2为振速的二阶量,故式(5)中声辐射力大小与p2成正比,式(6)在颗粒静止(u=0)时,声流曳力也与p2成正比关系,表明在声场强度增大的过程中,声辐射力与声流曳力的相对大小是一致的,合力在空间内的方向分布没有发生变化,颗粒在声场中的束缚状态不变。这里提到的状态不变是因为忽略了颗粒的重力与浮力,在实际应用中需要通过调节声场强度的大小来补偿其他作用力,调节操控位置。
4 水下颗粒操控实验
4.1 实验平台
本文搭建的水下颗粒操控实验平台如图10所示,包括以下设备:(1) 机械夹持装置,可以调节夹持换能器的距离及角度;(2) 凹球面超声聚焦换能器,中心频率为2 MHz,曲率半径(焦距)为20 mm,孔径半径为9.07 mm,共轴平行相向固定;(3) 多功能信号发生器(NF-WF1974);(4) 功率放大器(NFHSA4101);(5)数字示波器(RIGOL-MOS5102);(6) 有机玻璃材质透明水槽。

图10 实验器件放置实物图Fig.10 Picture of experimental device placement
4.2 实验过程及结果
实验采用聚苯乙烯颗粒作为操控目标,选取了半径为150、75、37.5和7.5 μm的四种颗粒。由于聚苯乙烯颗粒密度略大于水,将颗粒倒入小烧杯中加水,静置会沉入杯底,实验时需要对颗粒进行搅拌,使其处于悬停状态后吸入滴管。
在实验前向水槽中加入蒸馏水浸没装置,调整两个换能器孔径平面距离为1.5倍焦距(30 mm),连接好设备后,控制信号发生器发射频率为2 MHz的正弦波连续信号,经过功率放大器后,示波器显示输入电压的峰-峰值为13.6 V。换能器开启后,使用滴管吸取包含颗粒的水溶液,重复多次向声波辐射区域添加颗粒,待颗粒的束缚状态稳定后进行实验记录。
不同尺寸颗粒的水下聚集状态如图11所示,半径为150、75 μm颗粒在换能器中轴线区域被束缚,对应于声场的局部驻波场区域,部分颗粒处于中轴上,其余颗粒稍微偏离中轴1~2 mm,位置近似于图9(b)的三处合力零值点。随着颗粒尺寸的减小,颗粒的聚集程度减弱,分散地分布在辐射声场范围内,当颗粒半径减小到7.5 μm时,颗粒已经无法完成束缚,添加的颗粒会随着声流向两侧缓慢移动。

图11 不同尺寸颗粒的水下聚集状态Fig.11 Underwater aggregation of particles with different sizes
同时颗粒操控的稳定程度也随半径减小而减弱。其中对尺寸为 150 μm 的颗粒操控最为稳定,可以跟随夹持设备一同缓慢移动,但颗粒尺寸减小到37.5 μm后,受到水域的微扰动便会有粒子离开辐射区域,颗粒尺寸越小稳定性越差。
5 结 论
本文通过计算机仿真水下颗粒操控系统的声场、声流场和颗粒操控动态过程,验证了热黏性流体中的声辐射力理论和时间平均势能理论,进行了颗粒的作用力分析与水下颗粒操控实验,得到的结论如下:
(1) 仿真仅考虑了颗粒在水中操控过程中受到的声辐射力与声流曳力。颗粒在驻波声场中会聚集并束缚在声波波节位置,该位置对应于平均势能场的最小值。在颗粒的纵向聚集过程中,局部驻波场的纵向声辐射力为主导力,其数值远大于同向的声流曳力;横向聚集取决于横向声辐射力与曳力的相对大小,在颗粒尺度变小的过程中,声流曳力渐渐成为主导力,此时依靠声辐射力将无法对颗粒进行操控。
(2) 仿真中流场分布没有发生变化的前提下,声场强度的改变,声场内任意位置处的两种力的相对大小不变,即合力的方向不变,颗粒的操控模式不变,合力大小与声场声压值的平方成正比。但实际情况中,考虑颗粒受到的重力、浮力及环境扰动后,声场强度的增大可以增强颗粒的操控与抗扰动能力。
(3) 水下颗粒操控实验的结果验证了第一条结论,换能器辐射形成的局部驻波场可以依靠声辐射力稳定地聚集颗粒,但随着颗粒的尺寸减小,颗粒分布逐渐分散,声辐射力不再作为主导力,若想对该尺寸下的颗粒进行聚集,需要依靠声学微涡流等方式实现目标。

