基于CFD的船用核动力装置边界电磁阀泄漏流噪声场仿真研究
吴猛猛,张 鑫,杨家轩
(1. 海军潜艇学院,山东青岛 266199;2. 中国科学院声学所,北京 100190)
0 引 言
电磁阀在管路系统中起到接通和阻断管路中工作介质的作用,适用于高温、高压、介质为饱和热水或蒸汽的自动控制系统中[1]。电磁阀作为船用核潜艇核动力装置边界阀门,是稳压器压力水位控制的重要设备。一旦该阀发生内漏,将会对核动力装置运行安全造成严重影响[2]。例如美国三里岛核事故的发生,其中一个很重要的原因就是稳压器的释放阀内漏造成的;再如2015年10月美国康涅狄格州一座核电站发生一起低级别的紧急事件,也是由关闭冷却系统上的安全阀泄漏引起的。
本文在分析阀门泄漏流噪声机理的基础上,构建了船用核动力装置边界电磁阀的模型,利用Flucnt流体分析软件对电磁阀内漏的流场和声场进行仿真,并对影响流场和声场的各种因素进行研究。
1 理论基础
压力管路阀门泄漏时,流体在压差作用下经阀门不密封处(缝隙)流出,并呈束状喷射,即形成喷射射流。图1给出了泄漏孔处的射流速度变化。泄漏孔处的射流初始速度为u0,泄漏孔直径为D。从泄漏孔快速流出后与周围静止流体相互作用形成不同速度分区:混合区、过渡区和充分发展区[3-4]。在混合区,射流中充满涡旋,对周围流体产生卷吸效应,被卷吸的流体与射流一起运动;在过渡区,由于射流与周围静止的黏性流体发生掺混,阻力增大,边缘流速降低;在充分发展区,射流发展到射流边界层和射流中心,并全面发展成紊流[5]。
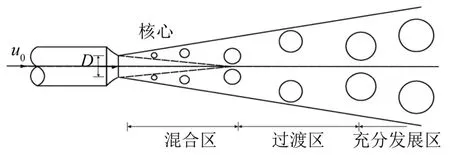
图1 射流速度示意图Fig.1 Schematic diagram of jet velocity
阀门内漏产生噪声与湍流射流中的旋涡结构的产生与发展有直接关系[6-7]。流体流动的本质是涡运动,当雷诺数Re较小时,流动状态为层流,并呈稳定涡或层流涡街的状态;随着雷诺数Re的增大,层流向湍流状态转变,并由线性涡街向湍流涡街发展。当阀门内漏时,阀门附近开始产生涡,且尺度逐渐增大,涡量增强,引起流噪声的急剧增大,因此阀门内漏流场旋涡是阀门内漏噪声产生的主要原因。同时阀门内漏的孔径大小、管内介质流速等是影响阀门涡量的主要因素[8]。

根据式(1)可知,阀门的内漏噪声主要与阀门结构形式、阀门前后压差、流体种类以及阀门是否空化等因素相关[9-10]。本文主要通过数值模拟研究阀门的工作压力、阀门流体种类以及阀门空化等因素对阀门内漏的流场和声场的影响。
2 数值模拟
利用ANSYS Flucnt流体分析软件对电磁阀内漏流场和声场进行仿真计算,具体方法如下:首先利用CAD软件构建电磁阀模型,然后利用ANSYS软件包 mcsh软件进行网格划分,之后再进行流场仿真计算,同时基于 Ligthill的声比拟方法进行声场计算,最后得到阀门内漏的流场和声场分布[11-13]。
2.1 模型描述
2.1.1 模型构建
首先以电磁阀中剖面为研究对象。选取的边界电磁阀的类型为套筒式高温高压电磁阀,主要由阀体、活塞组件、套筒、中法兰、导向体、阀套组件等零部件组成。该电磁阀具有结构简单、尺寸小、质量轻、操作简单、动作迅速可靠、高防护性等优点[14]。
利用CAD创建了电磁阀模型,取计算区域(x,y方向的尺寸)为 825、62 mm。为保证流道截面模型与真实流体截面吻合,阀体边界和阀芯外形处均保持与阀门设计图纸形状尺寸一致,图中标出的为电磁阀泄漏通道,如图2所示。
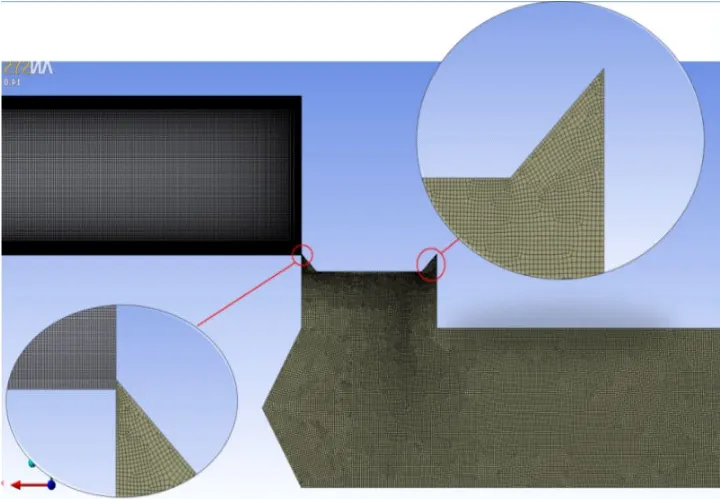
图2 电磁阀模型及其网格划分效果Fig.2 Model of solenoid valve and meshing dividing result
2.1.2 网格划分
利用ANSYS软件包mcsh软件对阀门流道结构模型进行网格划分,采取四边形和三角形混合网格(Uniform Quad/Tri)的划分方法,同时在尺寸变化很大的局部区域采取由边到面进行网格划分,通过控制线网格的数量及疏密程度,实现对面网格质量控制的目的。电磁阀模型在 1%开度时网格数量为335 179,Elcmcnt Quality大于 0.5的网格占比为82.1%,Aspcct Ratio小于5的网格占比为83.0%,网格质量较好,能够满足电磁阀内漏流场和声场仿真的要求。
2.1.3 边界条件设定
阀门模进出口边界为压力边界,进口压力根据需要设置,出口表压力为0 MPa,流场为水、空气或混合相,其他面为壁面。
2.2 结果分析
2.2.1 稳态模拟
稳态模拟方面,湍流模型采用Rcalizablc k-ɛ模型,壁面函数为标准壁面函数,得到电磁阀内漏的稳态流场分布,之后激活 ANSYS Flucnt的宽频(Broadband)噪声模型,可以得到电磁阀内漏的稳态声场。
(1) 流场分析
图3中给出了压力水管路和压缩空气管路电磁阀的速度云图。由图3可以看出,电磁阀内漏时会在泄漏孔处及下游引起速度场和湍流强度场的扰动,形成内漏射流场。同时压力水管路电磁阀的流场速度明显小于压缩空气管路电磁阀。
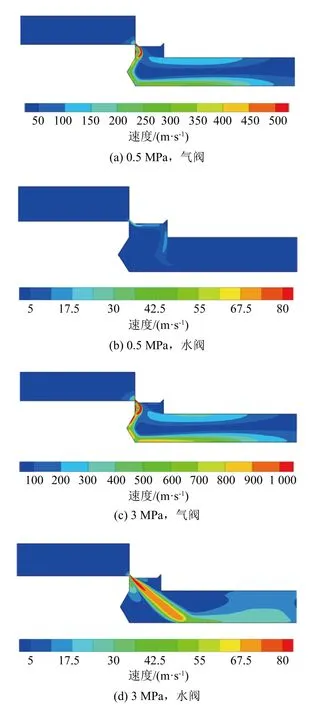
图3 电磁阀模型内漏流场速度分布云图Fig.3 Nephogram of flow velocity distribution in solenoid valve model
(2) 声场分析
图4中给出了压力水管路和压缩空气管路电磁阀内漏声场的声功率级云图,图5给出了声功率级随压力变化的曲线。
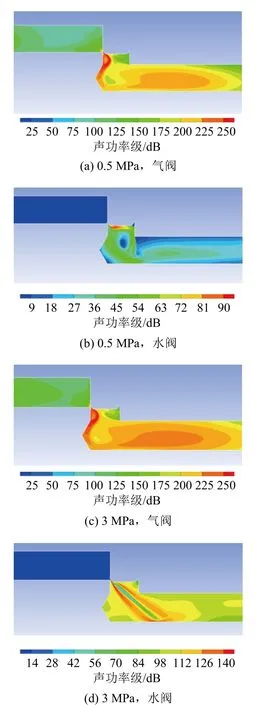
图4 电磁阀模型声功率级云图Fig.4 Nephogram of sound power level of solenoid valve model
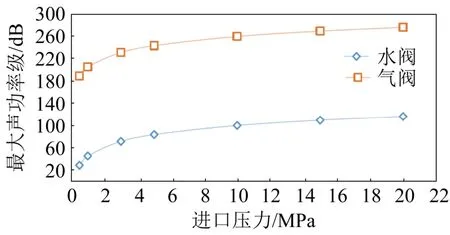
图5 最大声功率级随压力变化曲线Fig.5 Maximum power level versus pressure curve
由图4、图5可以看出:(1) 电磁阀内漏流场扰动时会激发声场变化,声功率级云图与流场分布有一定的近似性;(2) 压力水管路阀门内漏声场的声功率级值小于气阀;(3) 压力管路电磁阀内漏声场的声功率级值随着压力的增大而增大,并且在压力较小时(0~5 MPa)增幅最大。
(3) 空化影响
图6给出了压力水管路电磁阀内漏流场气化容积比云图分布。图7给出了不同压力下电磁阀内漏空化对声功率级影响的曲线,此处电磁阀的泄漏度(泄漏孔径与阀门通径之比,下同)为5%。由图6和图7可以看出:(1) 压力水管路电磁阀内漏时会在泄漏孔处发生空化,并且空化容积比随压力的增大而升高,当压力为0.5 MPa时,电磁阀泄漏孔处几乎无气化,压力达到3 MPa时,电磁阀下游有明显空化;(2) 空化效应对阀门内漏的流场分布和声场分布产生影响,区别于不考虑空化的情况;(3) 压力水管路电磁阀内漏声场的声功率级值随着压力的增大而增大。但是考虑空化比不考虑空化的情况最大声功率级平均高出20.32 dB。
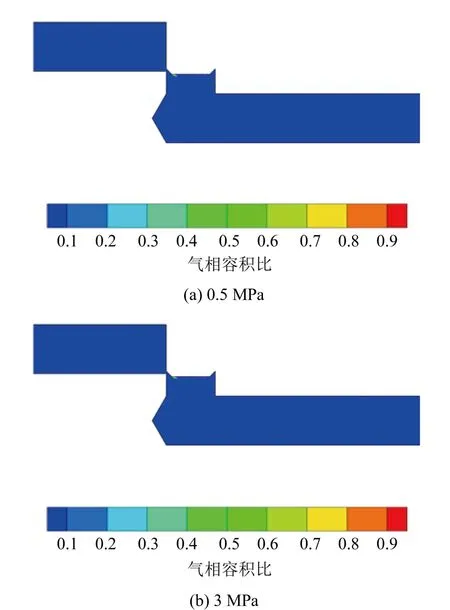
图6 电磁阀模型内漏流场气相容积比分布云图Fig.6 Nephogram of gas volume ratio distribution in leakage flow field of solenoid valve model
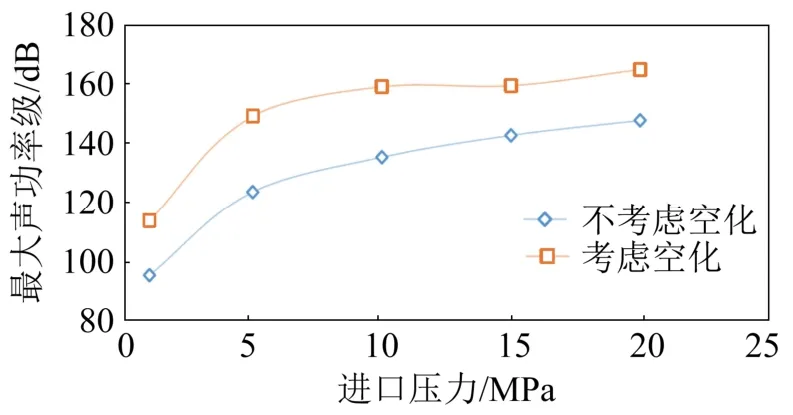
图7 电磁阀空化对声场的影响曲线Fig.7 Influence curve of electromagnetic valve cavitation on sound field
2.2.2 非稳态模拟
本文采用尺度自适应模型(Scalc Adaptivc Simulation, SAS)和福克斯·威廉姆斯-霍金斯方程(Ffows Williams-Hawking, FW-H),进行阀门内漏流场和声场的非稳态计算,得到阀门内漏的瞬态流场和声场。
(1) 流场分布
图8为相同条件下不同时刻电磁阀模型内漏速度场分布,此时管内介质为3 MPa压力水,阀门泄漏度为5%。由图8可以看出,电磁阀的内漏流场以射流的方式展开,开始阶段在泄漏孔处生成射流,随后沿着壁面向下游运动;运动过程中,射流中心逐渐明显,并形成卷吸效应,卷吸周围流体一起向下游运动;当时间t=10 ms时,电磁阀泄漏孔后流场扰动剧烈,由层流状态向湍流状态转变。
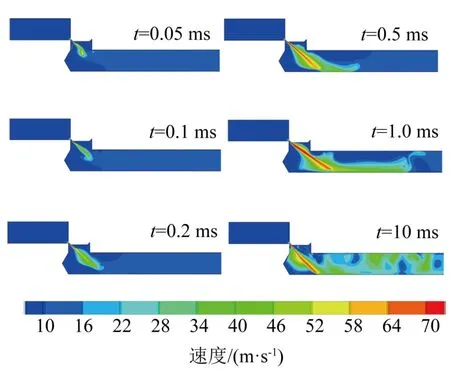
图8 电磁阀流场速度云图随时间变化Fig.8 Nephogram of flow field velocity variation of solenoid valve with time
(2) 声场分布
图9为工作压力为0.5 MPa时,电磁阀内漏声场总声压级随横向距离的变化曲线,图中横坐标为阀后横向距离X与电磁阀直径D的比值X/D,纵坐标为声场的总声压级值(dB)。由图9可以看出,在阀体处(X/D=0),湍流射流声场声压级值最大;之后在阀后(X/D=4)处出现第二个峰值,说明湍流射流在此处与管路壁面产生强烈冲击,之后沿管壁不断扩展,由于壁面摩擦等因素的影响,射流声场的声压级值随横向距离的增加不断衰减。
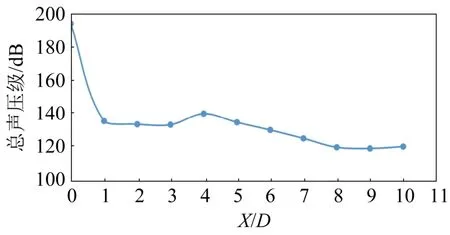
图9 电磁阀声场总声压级随横向距离的变化Fig.9 Variation of overall sound pressure level of solenoid valve with transverse distance
图10为同一监视点X/D=2时,电磁阀内漏声场总声压级值随工作压力的变化曲线。由图10可以看出,随着压力的增加,电磁阀内漏产生的湍流射流声场声压级值的增大,并且在压力较小时(0~5 MPa)变化最大。
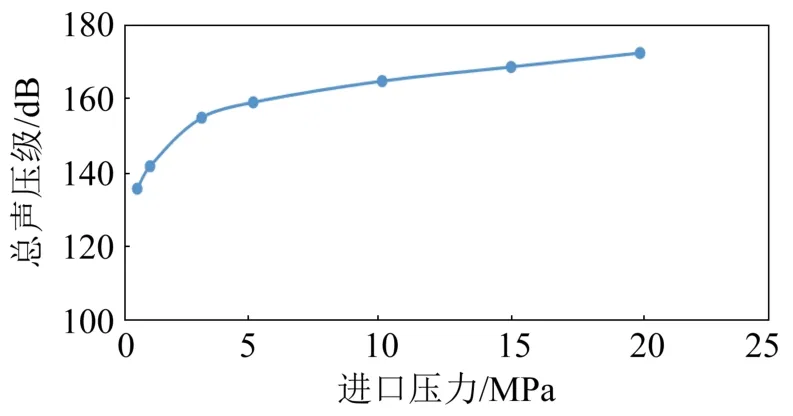
图10 同一监视点总声压级随工作压力的变化Fig.10 Variation of overall sound pressure level with working pressure at the same monitoring point
图11为同一监视点X/D=2时,电磁阀内漏声场总声压级值随阀门开度的变化曲线。由图11可以看出,在阀门开度为1%~10%时,随着阀门开度的增大,电磁阀内漏声场声压级增大,并且在阀门开度较小时(1%~5%)变化最大;当阀门开度大于10%时,由于射流的湍流度减小,流场趋于稳定,电磁阀内漏声场的总声压级趋于稳定。
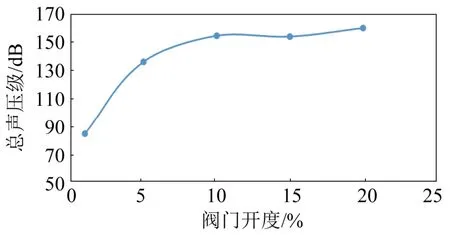
图11 同一监视点总声压级随泄漏度的变化Fig.11 Variation of overall sound pressure level with leakage at the same monitoring point
(3) 空化分布
图12给出了工作压力为3 MPa,阀门泄漏度为 5%的条件下、不同时刻电磁阀模型空化的气相容积比云图。此处管内介质为多相流,主相为水,第二相为水蒸气,采用的多相流模型为混合模型(Mixturc Modcl)。由图12可以看出,此条件下电磁阀的空化随着时间的推移,空化范围逐渐增大,初始阶段空化现象仅发生在电磁阀的泄漏孔处,之后随着电磁阀泄漏孔处射流沿壁面的扩展,空化范围随之发展,逐渐在管路下游大范围产生空化。
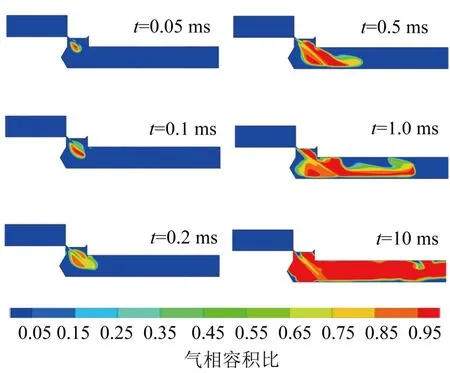
图12 不同时刻电磁阀模型气相容积比云图Fig.12 Nephogram of gas volume ratio of solenoid valve model at different times
3 结 论
本文主要利用 CFD软件对电磁阀内漏流场和声场进行仿真计算,研究结果表明:
(1) 宽频噪声模型得到的声功率级云图可用于阀门内漏声场的总体评价,快速确定阀门内漏声场分布情况;FW-H声学模型各监视点的声场信号经FFT处理后可得到阀门内漏声压级等细节信息。
(2) 阀门内漏的声场信号为宽频随机信号,随工作压力的增大而增强,并且在 0~5 MPa范围内增幅最大;相同条件下压力水管路阀门内漏声场强度小于压力气体管路阀门,因此可以采用动态增加压力的方式增强阀门内漏声场信号。
(3) 压力水管路阀门内漏时会发生空化现象,空化效应与工作压力、阀门泄漏度、阀门内部流道结构等因素相关,开度较小时更容易产生空化,流道截面变化处更易产生空化,并且空化随着工作压力的增大而增强;同时空化效应对阀门内漏的流场分布和声场分布产生影响,空化状态下阀门内漏声场的强度增大,因此在压力水管路阀门内漏声场计算时必须考虑空化效应。
(4) 阀门内漏流场和声场仿真计算为阀门内漏检测实验和实地测试提供了理论指导:(1) 测点选择上,阀体及附近位置的声场强度较大,因此可在阀体及其附近管路布置声信号监测点;(2) 测量条件上,声场信号随工作压力的增大而增强,压力过小时声场信号弱,因此可采用动态增加工作压力的方式检测阀门内漏;(3) 影响因素上,管内工作介质、阀门尺寸、阀门类型、测量位置等因素等都会对阀门内漏的流场和声场特征造成影响,因此在检测过程中必须考虑。

