一种用于水声材料设计的动态参数测试方法
杨婉雨,尹 铫,李 超,白国锋
(1. 中国科学院声学研究所,北京 100190;2. 中国科学院大学,北京 100049)
0 引 言
粘弹性材料如橡胶是常用的功能性材料。在水下减振降噪领域,超过90%的水下声学材料都是粘弹性材料,因此针对粘弹性材料声学性能的研究非常重要[1-2]。粘弹性材料动态力学参数是决定其声学性能的核心参量,由材料应力应变本构关系决定,因此材料的动态力学参数可以用本构模型表征。国内外学者针对粘弹性材料的动力学特性提出了许多种本构模型,其中分数阶导数模型能有效模拟粘弹性材料玻璃化转变区的连续松弛过程,并且能够描述材料在较大频率范围内的动态力学特性,近年来被广泛使用[3]。
用于水声材料设计中的材料动态参数,一般需要复数模量和泊松比。对于复数模量测试,总体可以分为两种方法:声学法和振动法。声学法通过测量材料的声学参数如反射系数和透射系数,反演得到黏弹性材料动态力学的参数,这类方法有声管法[4]、自由场衰减法[5]。这些方法的输出精度取决于反射系数、透射系数等声学参数的准确测试,但目前声学参数的测试精度仍然较低。振动法测量材料振动特性来计算其力学参数,一般有自由衰减法、强迫共振法和强迫非共振法等[6]。其中前两者仅能测量离散频率点的动态参数,无法满足水声材料宽频域设计的参数需求[7]。动态机械分析仪(Dynamic Mcchanical Analyzcr, DMA)是强迫非共振法代表性标准测试设备,在直接测量的频率范围内精度很高,但是由于直接测量的频率范围小,需要利用时间-温度等效原理得到材料宽频带内的动态力学参数,此种等效引起的测量误差尚无理论上的估计。泊松比的测试,需要通过测试得到材料的杨氏模量和剪切模量,从而计算获得材料泊松比。而弹性模量的测试,如前所述,其测试精度无法满足要求。
利用时温等效原理扩展测量材料的动态力学参数的频率范围传统方法是将不同温度下的复数模量沿对数频率轴平移重叠而得到主曲线图。这样的方法没有考虑到储能模量和损耗因子之间的内在联系,且在平移过程中会产生各种误差。Havriliak-Ncgami (H-N)模型克服了上述缺点,仅用4个与温度无关的变量和一个与温度有关的变量就可准确反映常用橡胶材料从橡胶态到玻璃态转化的整个力学参数变化过程,因此该模型可用于预测聚合物在较宽频率范围内的动态力学性能[8]。不同温度和频率的所有损耗因子-储能杨氏模量的数据在双对数轴上显示出来,会构成一条倒U曲线,称为Wickct图。Wickct图的形状与H-N模型中的松弛时间无关。因此Szabo等[9]利用DMA测试的复弹性模量数据反演出H-N模型中的4个与温度无关的变量;然后利用不同温度的DMA数据反演得到松弛时间;最后,利用不同的温度时间就可拟合得到Williams-Landcl- Fcrry(WLF)方程中的未知参数,继而计算氯丁橡胶和增塑性聚氯乙烯两种弹性体材料在不同温度和频率范围内的动态力学特性。研究结果表明,计算出的模量和损耗因子与实验值基本一致。Waltcr等[10]也提出了基于H-N模型的复数模量主曲线拟合方法,该方法在复杨氏模量测试随机误差达 10%的条件下仍然能准确地拟合出主曲线。随后,H-N模型被广泛应用于水下声学材料研究中[11-13]。
对于泊松比测试,Sim等[14]对两个不同形状因子(形状因子定义为样品半径与厚度比的一半)的圆柱形样品进行轴向激励,获得试样上下表面的振动传递函数,进而采用解析的方法计算表观杨氏模量。形状因子小的试样杨氏模量受泊松比影响小,表观模量即为真实材料模量,而形状因子大的试样表观模量对泊松比敏感。通过有限元拟合出形状因子较大的试样表观模量与真实模量比值随泊松比的变化曲线,通过迭代优化,即可寻找到泊松比。该方法较复杂,且需要形状因子差别很大的两个样品,制样与测试均不易操作。随后Langlois等[15]改进了这一方法,基于对圆盘形弹性试样在静压缩条件下的高阶轴对称有限元模拟,建立了压缩刚度、杨氏模量、泊松比和形状因子之间的多项式关系,进而利用两个形状因子试样压缩刚度的测试结果代入方程得到泊松比。
本文首先采用DMA对某丁腈橡胶进行动态力学参数变温测试,再将WLF方程代入到H-N模型中,直接利用不同温度和频率的DMA数据同时进行反演得到方程中未知的7个参数,继而计算得到复杨氏模量宽频域主曲线。这样的方法利用了所有不同温度和频率的测试数据对模型中的参数进行反演,简化了反演步骤。其次对文献[15]中的方法进行了改进,仅通过准静态压缩条件下的有限元模拟得到两种不同形状因子试样在不同泊松比下表观杨氏模量的比值,继而通过测试数据得到泊松比。这种方法省去了两次单独拟合的工作,同时消除了测试装置本身对于结果的影响,提高了测试效率。最后,将宽频域内的复杨氏模量和泊松比代入分层介质模型进行声学性能计算,并与声管测试结果进行对比。
1 复杨氏模量宽频域主曲线拟合
1.1 H-N复数模量模型


1.2 主曲线拟合原理及结果
聚合物的同一力学松弛现象可以在较高温度、较短时间观察到,也可以在较低温度、较长时间内观察到。因此,升高温度与延长观察时间对分子运动是等效的,对聚合物的粘弹性行为也是等效的,这就是时间-温度等效原理。1955年,化学家Williams,Landcl和Fcrry共同提出WLF方程用来描述时温等效原理[16]:

其中,αT为移位因子,C1、C2是两个经验参数,取决于参考温度T0的取值。移位因子αT可以表示温度T下的松弛时间与参考温度T0下的松弛时间之比,即:

因此可得:

对于流变简单材料,在温度T下测量的频率为f的模量等于在温度T0下测量的频率为f0的模量。利用 WLF方程,可以将不同温度下一定频率范围内的测试结果通过平移来获得较宽频率范围内的动态力学参数,用于后续橡胶材料声学性能计算。
利用 DMA对橡胶样品进行-10℃、-6℃、-4℃、2℃、8℃、14℃、20℃、29℃这8个不同温度台阶,在1~250 Hz频率范围的动态参数测试,测试设备如图1所示。将WLF方程引入H-N模型中,根据对7个参数E0、E∞、α、β、C1、C2、τ0的识别,可获得任意参考温度下材料参数宽频域主曲线。定义目标函数为所有储能模量、损耗因子测试结果与 H-N方程计算结果的相对误差绝对值之和,即:

图1 基于DMA450的复杨氏模量变温试验Fig.1 The experiment of the complex Young’s modulus test over a wide range of temperatures based on DMA450
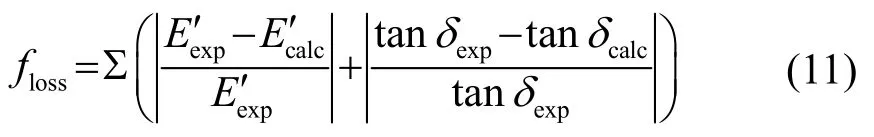
式中:floss为目标函数;分别为测试和计算的储能模量;tanδcxp和 ta nδcalc分别为测试和计算的损耗因子。
采用信赖域反射算法[17]对参数优化,使得目标函数最小。得到参数后代入H-N方程中获取参考温度为 0℃时储能杨氏模量和损耗因子的主曲线,如图2和图3所示。
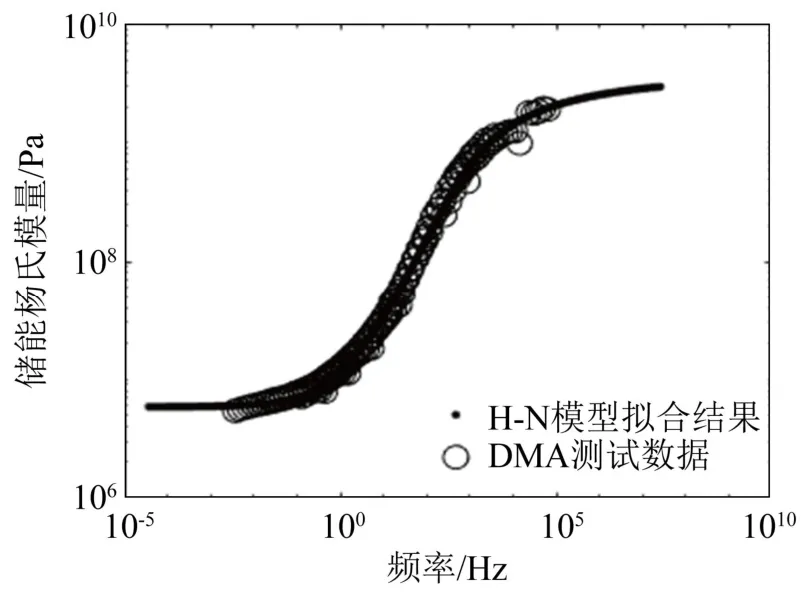
图2 参考温度为0℃时,丁腈橡胶储能模量主曲线Fig.2 The storage modulus master curve of nitrile rubber at the reference temperatureT0=0℃
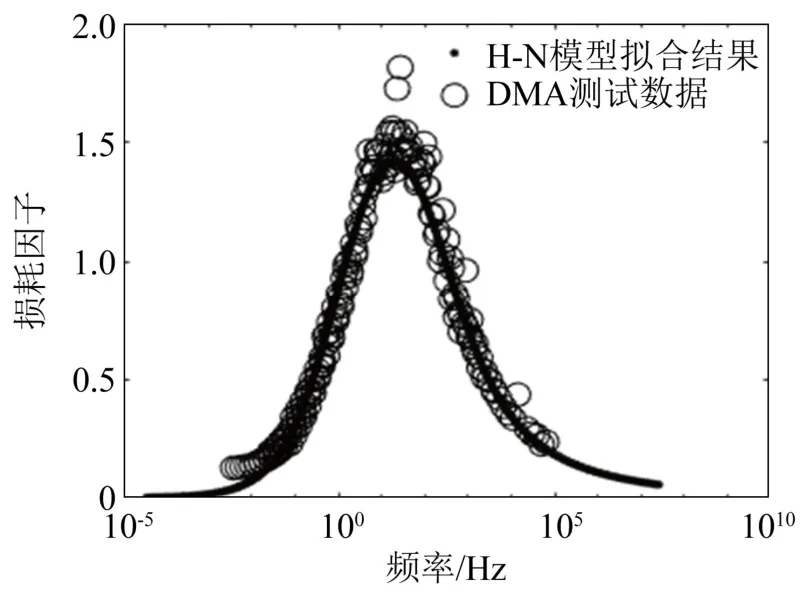
图3 参考温度为0℃时,丁腈橡胶损耗因子主曲线Fig.3 The loss factor master curve of nitrile rubber at the reference temperatureT0=0℃
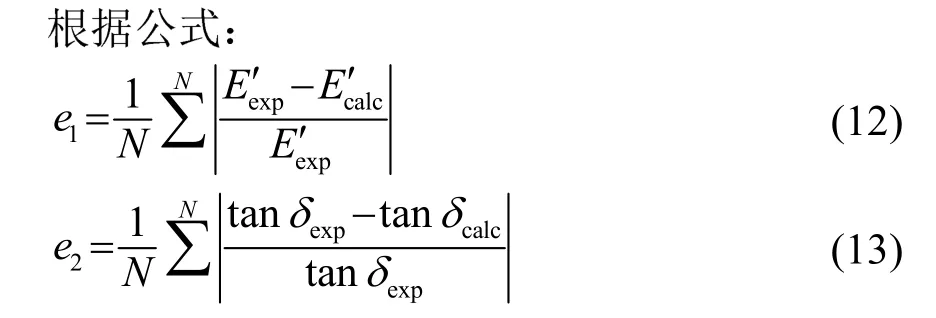
计算得到全频段内储能杨氏模量和损耗因子的平均相对误差e1、e2。结果表明,基于H-N模型得到的主曲线与DMA测试结果相比,储能杨氏模量和损耗因子的平均相对误差均在10%的范围内,验证了该方法的可靠性。
2 泊松比测量
2.1 基本理论
将前述材料制成圆柱形试样,固定在两块钢板之间,测试装置如图4所示。

图4 机械阻抗测试装置Fig.4 The measurement setup for the mechanical impedance test
激振器在底部产生0~100 Hz频段的扫频信号激发底板。力传感器安装在顶板上,测试施加在顶板上的反作用力F(ω)。加速度计固定在底板上,测到底板的加速度,再经过两次积分就可以得到其位移u(ω),进而得到机械阻抗即[15]:

在低频情况下,机械阻抗可以写成:
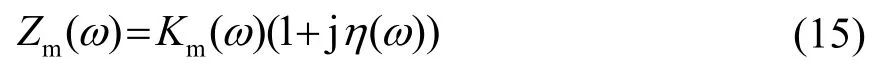
式中:Km(ω)为角频率ω下试样的压缩刚度;η(ω)为损耗因子。
对于截面积为A,半径为r,长度为L的圆柱,其表观杨氏模量与压缩刚度存在线性关系,即:

再将其归一化,可得:

其中,E是真实杨氏模量。
对于形状因子s(形状因子定义为样品半径与厚度比的一半,即s=r/ (2L),通常s≥0 . 025)较大的试样,泊松比对归一化表观杨氏模量影响较大。因此基于图4的装置,对形状因子s1=0.5和s2=0.25的试样进行有限元仿真,得到其归一化表观杨氏模量。由于这两个试样来自于相同的材料,所以它们具有相同的杨氏模量E、泊松比v和损耗因子η。
通过建模发现,在0~100 Hz频率范围内,归一化表观杨氏模量的大小与频率几乎无关,与其真实杨氏模量也无关,而只与材料的形状因子和泊松比有关,如图5所示。
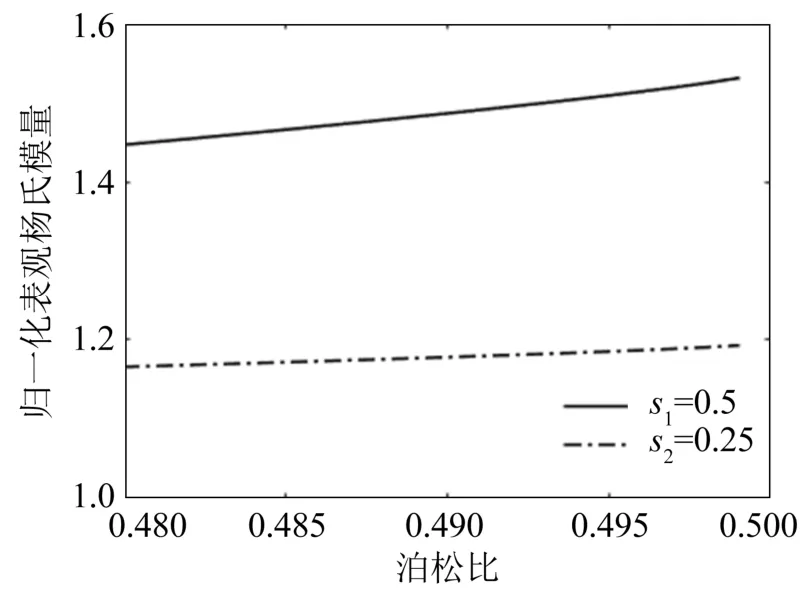
图5 两种形状因子s1=0.5和s2=0.25的试样归一化表观杨氏模量随泊松比的变化Fig.5 Variations of normalized apparent Young’s modulus with Poisson’s ratio for the two samples with different shape factorss1=0.5 ands2=0.25
因此,对于这两种形状因子的试样,其归一化表观杨氏模量可以写成:

将上述两式相比可得:

在固定的两个形状因子s1和s2下,泊松比v与两个表观杨氏模量之比R是一一对应的关系,因此可将泊松比v用R来表征,即:
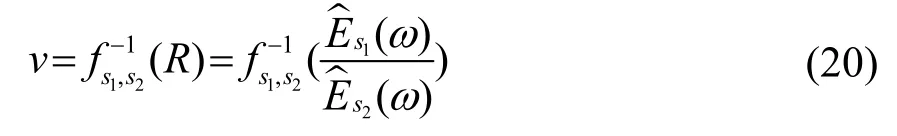
2.2 泊松比试验验证
基于图4的测试装置,分别对形状因子s1=0.5和s2=0.25的试样进行机械阻抗的测量,根据式(15)和式(16)可以得到两个试样的表观杨氏模量和。由于系统在50~80 Hz的频率范围内较为稳定,因此选取这一频率范围内两个试样的表观杨氏模量,结果如图6所示。
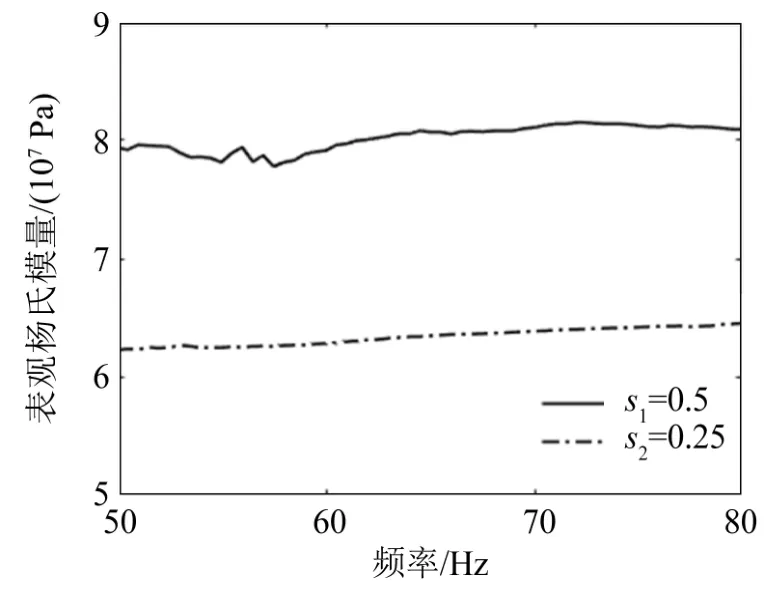
图6 测量的两种形状因子s1=0.5和s2=0.25试样在50~80 Hz频率范围内的表观杨氏模量Fig.6 The measured apparent Young’s modulus of two samples with different shape factorss1=0.5 ands2=0.25 in the frequency range of 50~80 Hz
表观杨氏模量之比R与泊松比v相互依赖的定量关系可以利用局部加权回归得到,因此将测量得到的表观杨氏模量之比R(ω)带入到回归模型中即可得到试样的泊松比,结果如图7所示。在 50~80 Hz的频率范围内,泊松比的平均值和标准差分别是0.491 37和0.003 44,由于实际橡胶材料的泊松比在 0.49~0.495之间,因此可认为该测量结果与实际相符。
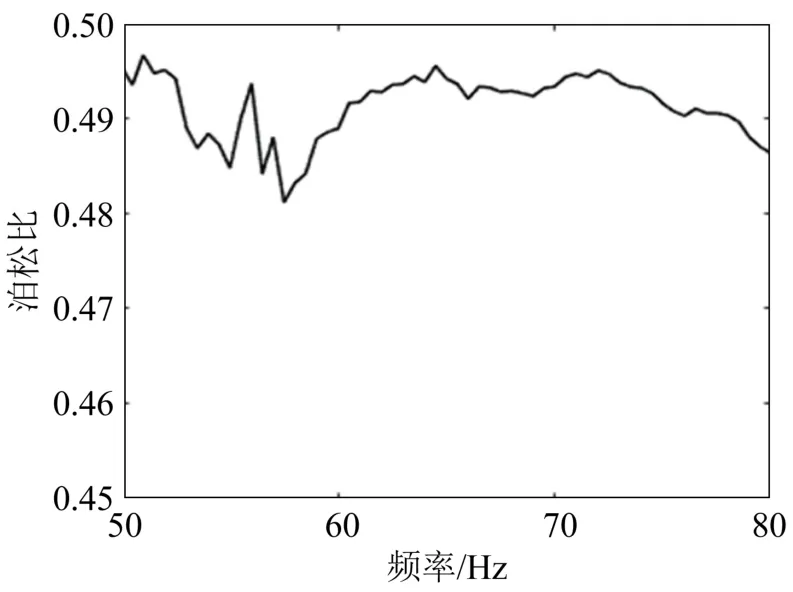
图7 50~80 Hz频率范围内的泊松比Fig.7 The measured Poisson’s ratio in the frequency range of50~80 Hz
3 吸声系数实验与计算
将前述橡胶材料制成直径为 55 mm、厚度为50 mm的声管样品,放置在管中进行反射、透射、吸声系数测试,测试频率范围为3~30 kHz。同时,应用分层介质传递矩阵模型计算其吸声系数,计算模型如图8所示,图中的介质为橡胶材料,其厚度为D。
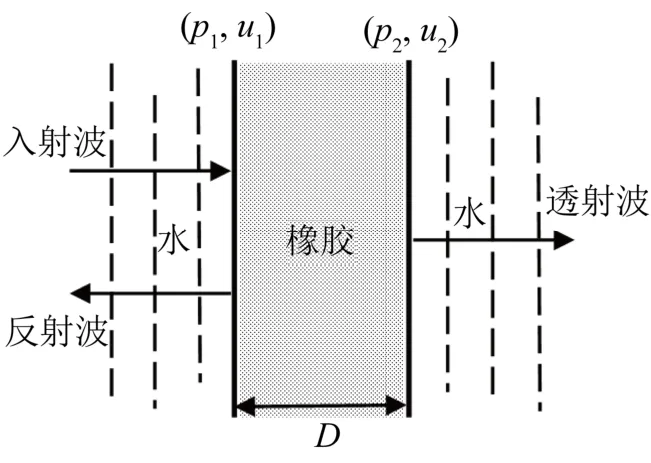
图8 分层介质传递矩阵计算模型Fig.8 Calculation model of transfer matrix in the layered medium
水-橡胶界面声压p1和法向振速u1与橡胶-水界面声压p2和法向振速u2关系为[18-19]
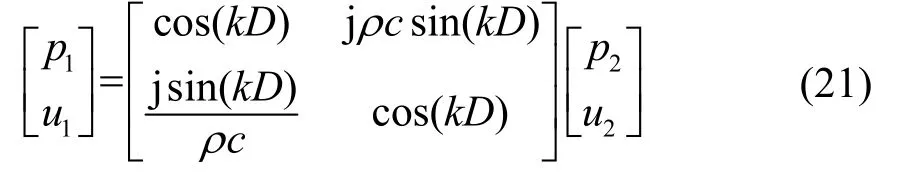
式中:ρ为橡胶材料的密度;由于只考虑垂直入射的情况,c为橡胶材料中的纵波声速;k为其对应波数。其中,声速与材料本身的性质有关,即:
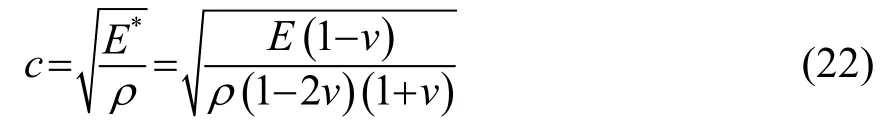
式中:E、v分别是材料的杨氏模量和泊松比。
根据式(21)、(22),可得到表面的声阻抗率为

垂直入射条件下,声反射系数rp和透射系数tp算公式为

式中:ρ0、c0分别为水的密度和声速。吸声系数为

根据前述模型得到的杨氏模量和泊松比代入式(22),并根据式(21)~(25)计算吸声系数。计算结果与声管测试结果对比如图9所示,由图可知,两者相吻合,验证了前述材料动态参数测试方法的准确性。分别计算v±0.003 4时 0~10 kHz范围内吸声系数的变化情况,如图10所示。结果表明,泊松比变化0.003 4造成吸声系数的变化均在0.1的范围内,但泊松比如此微小的变化对吸声系数仍产生较大影响的结果证明对材料的泊松比进行准确测量是决定吸声系数计算准确性的重要因素。
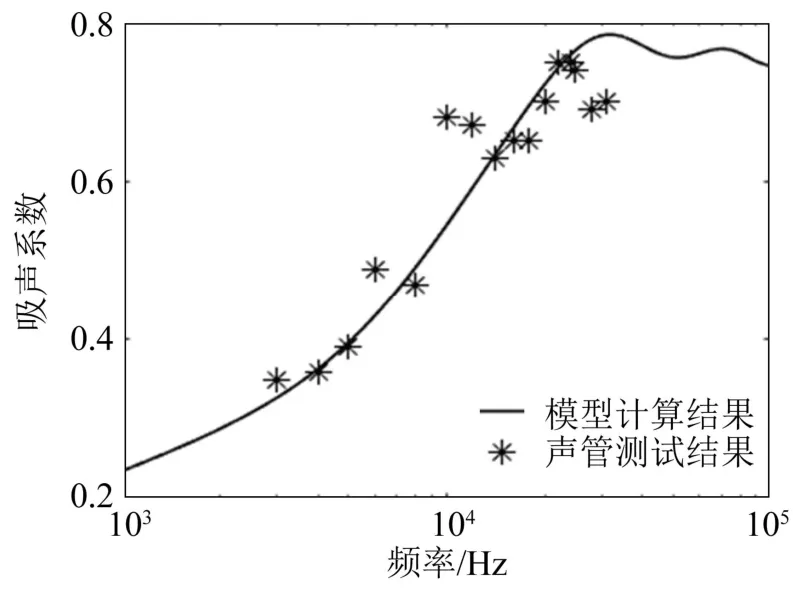
图9 橡胶吸声系数的模型计算结果与声管测试结果对比Fig.9 The comparison between the model calculated results and sound tube tested results of the sound absorption coefficient of rubber
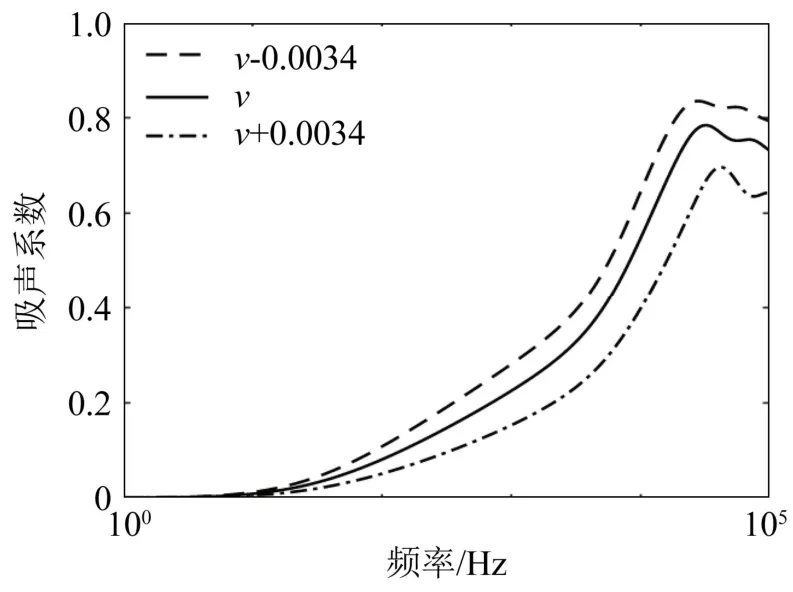
图10 泊松比变化±0.003 4对吸声系数的影响Fig.10 Effects of Poisson’s ratio change of ±0.003 4 on sound absorption coefficient
4 结 论
本文首先提出了一种复杨氏模量及泊松比准确测试的方法。该方法将WLF方程引入到H-N复数模量模型中,直接利用不同温度和频率的 DMA数据并采用信赖域反射算法进行反演得到方程中的未知参数,并准确拟合得到了储能杨氏模量和损耗因子宽频域主曲线。与DMA测试结果相比,储能杨氏模量和损耗因子的平均相对误差均在 10%以内。
其次,泊松比的测试方法是在Langlois等提出方法的基础上进行改进。根据同一材料不同形状因子表观杨氏模量之比与泊松比存在唯一量化关系的特性,通过对两种不同形状因子试样准静态的有限元模拟,获得不同表观杨氏模量比值与泊松比量化曲线,再根据橡胶样品表观杨氏模量的测试结果,利用局部加权回归获得其泊松比。该方法的优势在于省去了两次单独拟合的工作,提升了测量效率,同时消除了测试装置本身对于结果的影响。结果表明,泊松比的平均测量值在实际范围之内,而标准偏差为0.003 4,与原有方法中基本一致,因此可以认为本文改进的泊松比测量方法可靠。
最后,制作出直径55 mm、厚度50 mm的声管样品进行吸声系数测试,同时将复杨氏模量、泊松比的测试结果带入分层介质模型中进行吸声系数计算,吸声系数测试结果与计算结果相吻合,验证了上述测试方法的正确性和有效性。通过计算泊松比对吸声性能的影响发现,泊松比的千分位微小变化会造成吸声系数的较大改变。本测试方法提高了动态参数的测试效率,为提高水声材料设计中的动态参数输入精度提供了新的解决方法。

