石墨烯薄膜热声性能的三维数值计算与测试

张诣强，李 双，范学良，李 成，唐金龙

（1. 苏州大学轨道交通学院，江苏苏州 215131；2. 桂林电子科技大学广西密码学与信息安全重点实验室，广西桂林 541004 ）

0 引 言

1917年，Arnold和Crandall首次系统性地阐述了热声的发声机制，并且建立了交流电通过薄层导体的模型，不过由于当时的材料限制，只是检测到微弱的声音[1]。1978年，F.Alan Mcdonald和Grovcr C. Wctscl建立了典型的光声模型，并且得出了声波方程的一维近似解析解[2]。1999年，我国声学家马大猷对热声理论进行了系统阐述[3]。

近年来，纳米技术突飞猛进，给基于热声效应扬声器的研究开辟了一条新的路径[4]。2008年，Xiao等发现通电的碳纳米管薄膜会在其周围产生声波[5]。2011年，Tian等制作了纸质材料为基底的石墨烯薄膜扬声器，并且对其做了发声实验[6]。2012年，Suk等探究了不同基底下石墨烯薄膜的发声情况[7]。2015年，王严冬等对多孔硅热致发声进行建模研究[8]，Fci等制备出三维石墨烯泡沫扬声器，此类扬声器优于其他石墨烯薄膜扬声器[9]。2016年，Kim等做了三维还原石墨烯扬声器的阵列[10]和聚合物网格支撑的石墨烯薄膜发声实验[11]。

Tian和Suk等在实验中发现声压和输入功率成正比，并且得出了声压随频率的变化规律，但是对模型缺乏系统的理论分析[6-7]。Vcstcrincn等使用格林函数法给出了考虑基底吸收热对声压的影响，并且提到瑞利距离的概念，但没有考虑薄膜单位面积热容量的影响[12]；Xiao等在Arnold和Crandall的热声模型的基础上考虑薄膜的自身热容，但是声压表达式仅适用于远场（瑞利距离之外）[13]。Hu等在Mcdonald和 Wctscl建立的光声模型基础上，推导出了一般固体的热致发声模型的一维解析解[14]；Lim等将声场分成近场和远场，瑞利距离之内是平面波，瑞利距离之外是球面波，推导出了无基底石墨烯薄膜的一维近似声压公式[15]。本课题组的卞安华等[16]和Xing等[17]推导出了考虑基底传热的一维近似声压公式，并且进行了实验的论证。

上述研究均是采用一维模型进行分析，计算的石墨烯薄膜声压分布并不连续，在瑞利距离处突变，但实际上声压分布是连续的，并且一维模型无法计算石墨烯表面的温度分布。本文将建立石墨烯薄膜的三维热传导和声扩散模型，进行数值计算，并将计算值与一维近似解析解及实验测试值进行对比分析。

1 石墨烯薄膜三维传热模型

通入交流电的石墨烯薄膜的温度特性由振荡温度和稳态温度分布描述。基底材料的电阻相对于石墨烯而言很大，可视作绝缘体。因此，假设石墨烯薄膜的热量全部由石墨烯的焦耳热产生。石墨烯的上表面分别与电极的下表面和空气接触进行传热，电极的上表面与空气进行对流换热，石墨烯的下表面与基底的上表面接触进行传热，而且基底的下表面与空气接触进行对流换热。由于基底的厚度为0.3 mm左右，石墨烯仅有10 nm，可以认为只有薄膜上下表面有热传导。考虑理想情况，假设石墨烯的电流密度的分布是均匀的。石墨烯的热传导模型如图1所示。

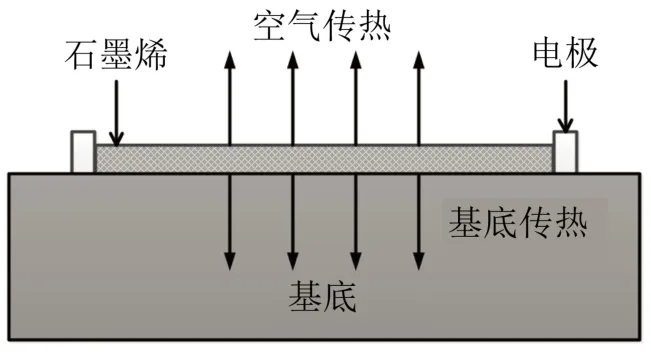
图1 石墨烯薄膜的热传导模型Fig.1 Heat conduction model of graphene film

1.1 石墨烯的焦耳热过程

1.2 基底传热过程

1.3 传热模型的数值计算

使用COMSOL Multiphysics进行数值计算，使结果可视化。其中用到的材料参数如表1所示。

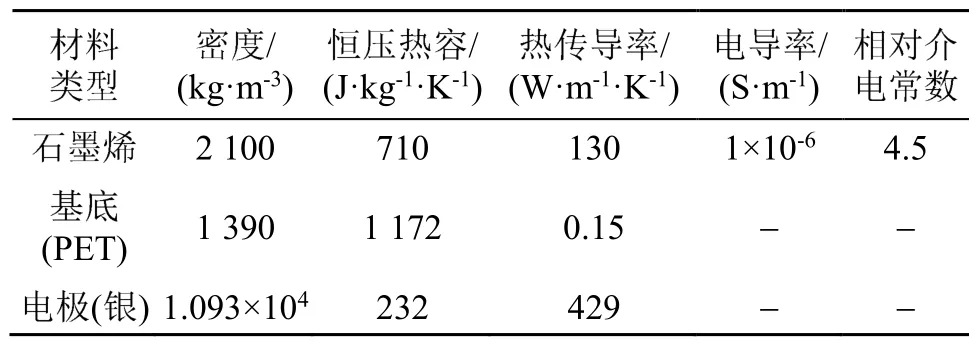
表1 材料参数Table 1 Parameters of the materials

（1） 温度振荡

石墨烯薄膜两端通入30 V的交流电（有效功率0.73 W），数值计算结果如图2所示。石墨烯薄膜的温度是随时间振荡变化的，振荡温度的幅值不随时间改变。由于振荡温度的幅值极小，频率较高，而温度测量仪的精度和帧率无法达到要求，则温度振荡部分仅能做理论分析。数值计算结果表明，温度振荡的幅值在石墨烯薄膜表面是均匀分布的，且温度振荡的频率是电流频率的两倍，这也很好解释了输出信号的频率是输入电信号频率两倍的现象。

在其他条件不变的情况下，当有效输入功率为0.73 W时，温度振荡的幅值随频率的增加而下降，如图3所示。

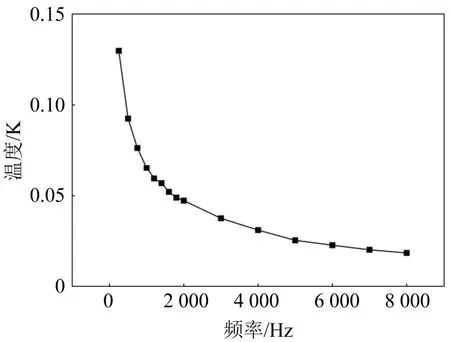
图3 温度振荡的幅值与温度振荡频率的关系Fig.3 Relationship between amplitude and frequency of temperature oscillation

（2） 温度稳态分布

由于温度振荡的幅值相对于石墨烯薄膜表面的温度是极小的，在研究石墨烯薄膜的温度分布时可以忽略温度振荡。图4为有效输入功率0.2 W时（测量稳态温度时，为避免长时间通入大电流导致损坏石墨烯薄膜，此处取相对较小的输入功率），石墨烯薄膜温度的稳态分布。从图4中可以看出石墨烯薄膜中央的温度最高，沿四周逐渐下降。

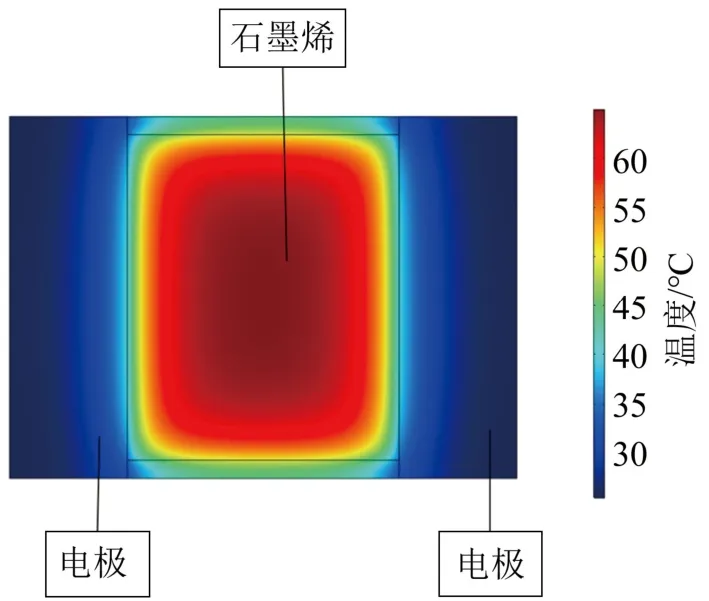
图4 石墨烯薄膜表面稳态温度分布Fig.4 Steady state temperature distribution of graphene film surface

2 三维声扩散模型及数值计算

石墨烯薄膜的热声效应是指石墨烯表面的温度振荡使得附近空气进行周期性的热胀冷缩，从而产生声波[15]。在得出石墨烯薄膜表面温度振荡幅度随频率的变化后，将其作为边界条件，建立声扩散模型。由于热黏性声学的计算量极大，且热损失仅在热边界层内损失很大，则可在靠近薄膜的小区域内考虑热黏性损耗，而其他部分依然利用传统压力声学的计算公式。声扩散模型如图5所示。

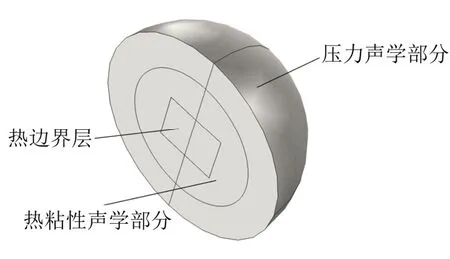
图5 声扩散模型Fig.5 Sound diffusion model

2.1 热黏性声学

2.2 压力声学

2.3 数值计算

使用COMSOL Multiphysics进行数值计算，使结果可视化。其中用到的空气参数如表2所示。

表2 空气参数Table 2 Parameters of air

（1） 热黏性声学部分的总压力分布

通过计算可得到热黏性声学部分声压的分布，其中频率为8 000 Hz时的声压分布如图6所示。等压线在靠近声源的地方曲率较小，而距离声源越远曲率越大，最后趋近于球面波。

图6 热黏性声学部分声压分布Fig.6 Sound pressure distribution of thermoviscous acoustic part

（2） 压力声学部分的声压分布

图7是频率为8 000 Hz时的压力声学部分的声压分布图，其规律符合一维解析解中远场声压近似于球面波的结论。

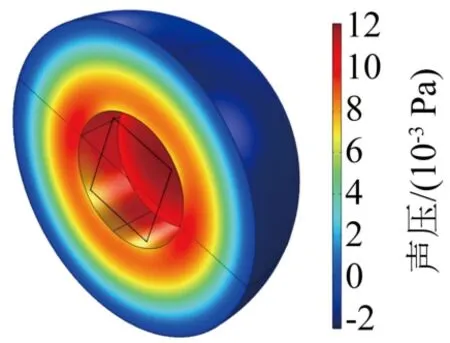
图7 压力声学部分的声压级分布Fig.7 Distribution of sound pressure level in the pressure acoustic part

3 石墨烯薄膜发声的影响因素

3.1 基底对石墨烯薄膜发声的影响

基底吸收了石墨烯薄膜产生的大部分焦耳热，因此基底对石墨烯薄膜发声效果有很大的影响。在其他条件不变的情况下，分别计算了基底的密度、恒压热容和导热系数对石墨烯发声的影响，结果如图8～10所示。从图8～10中可以看出，基底的密度、恒压热容和导热系数与石墨烯薄膜的声压级呈负相关。

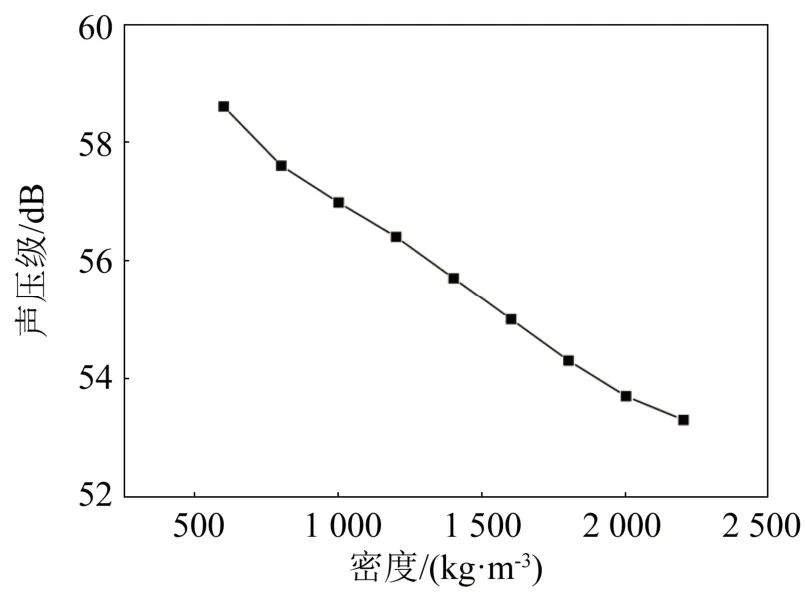
图8 基底密度与石墨烯薄膜声压级的关系Fig.8 Relationship between substrate density and sound pressure level of graphene thin films

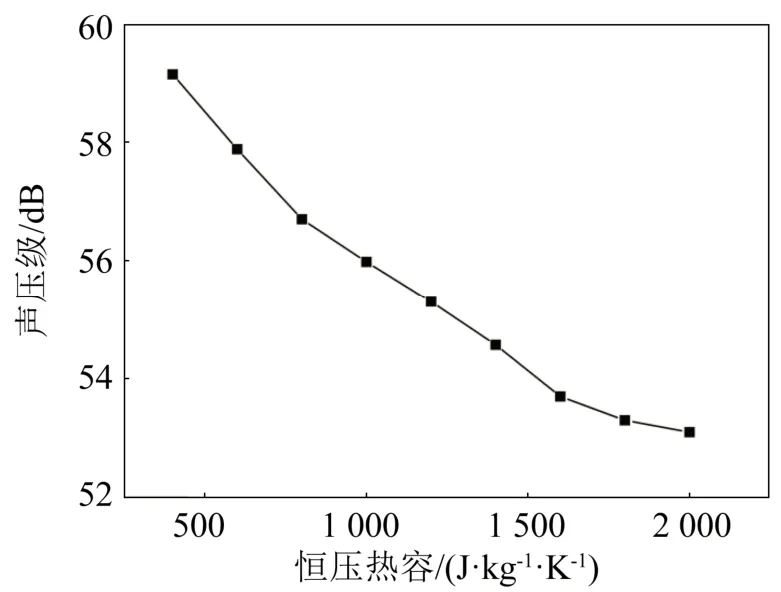
图9 基底恒压热容与石墨烯薄膜声压级的关系Fig.9 Relationship between substrate heat capacity at constant pressure and sound pressure level of graphene thin films

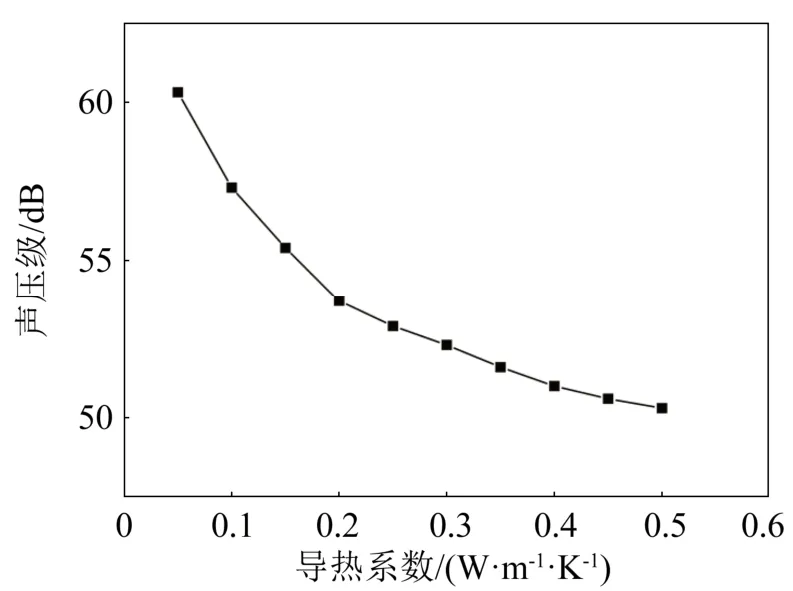
图10 基底导热系数与石墨烯薄膜声压级的关系Fig.10 Relationship between substrate thermal conductivity and sound pressure level of graphene thin films

3.2 气体对石墨烯薄膜发声的影响

气体作为声波传播的媒介，本身的参数对石墨烯薄膜的发声效果也很重要。在其他条件不变的情况下，分别计算了气体的密度，恒压热容和导热系数对石墨烯发声的影响，结果如图11～13所示。从图11～13中可以看出，气体的密度和导热系数与石墨烯薄膜的声压级成正相关，气体的恒压热容与石墨烯的声压级呈负相关。

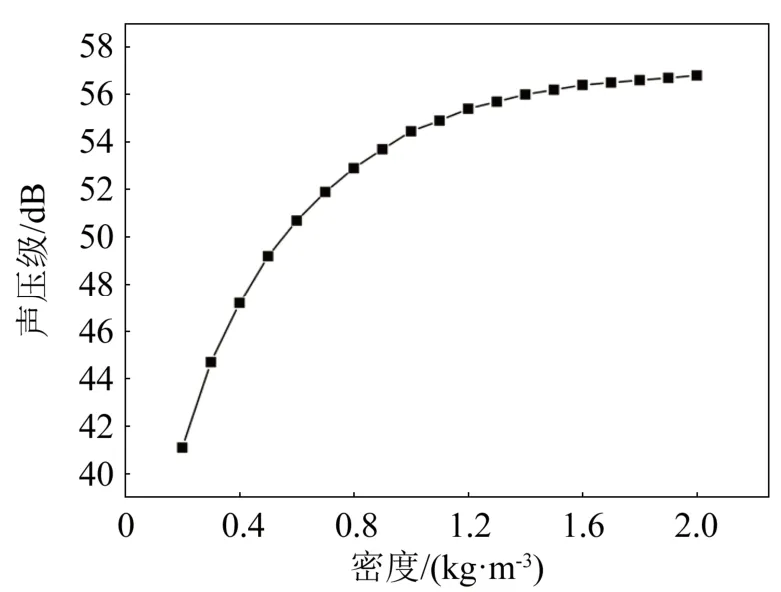
图11 气体密度与石墨烯薄膜声压级的关系Fig.11 Relationship between gas density and sound pressure level of graphene thin films

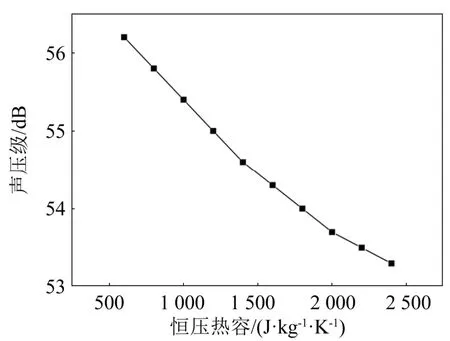
图12 气体恒压热容与石墨烯薄膜声压级的关系Fig.12 Relationship between gas heat capacity at constant pressure and sound pressure level of graphene thin films

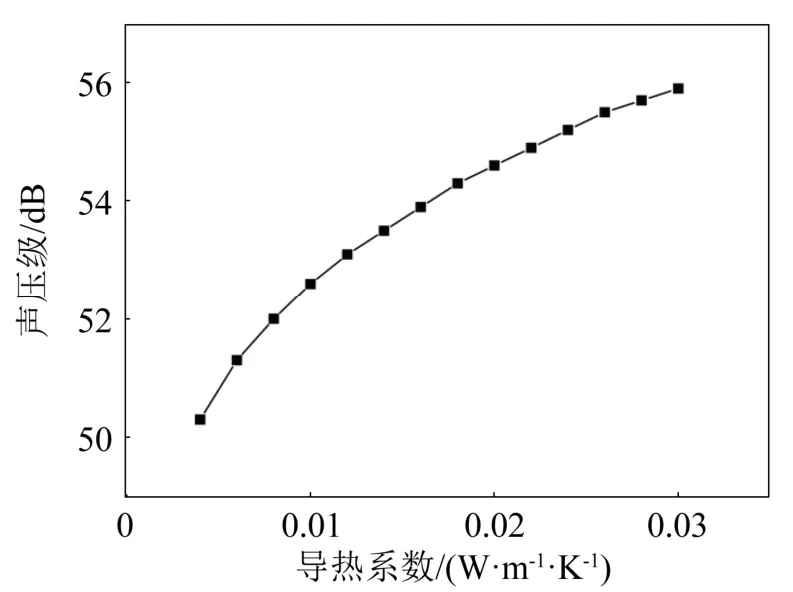
图13 气体导热系数与石墨烯薄膜声压级的关系Fig.13 Relationship between gas thermal conductivity and sound pressure level of graphene thin films

4 实验测试与对比分析

4.1 表面稳态温度分布测试

为了验证传热模型，设计传热实验如图14所示。实验中使用的石墨烯薄膜（PET基底）如图15所示。当输入功率为0.2 W时，待石墨烯薄膜的表面温度达到稳态，测试结果如图16所示，实验值与图4中的计算值基本吻合。

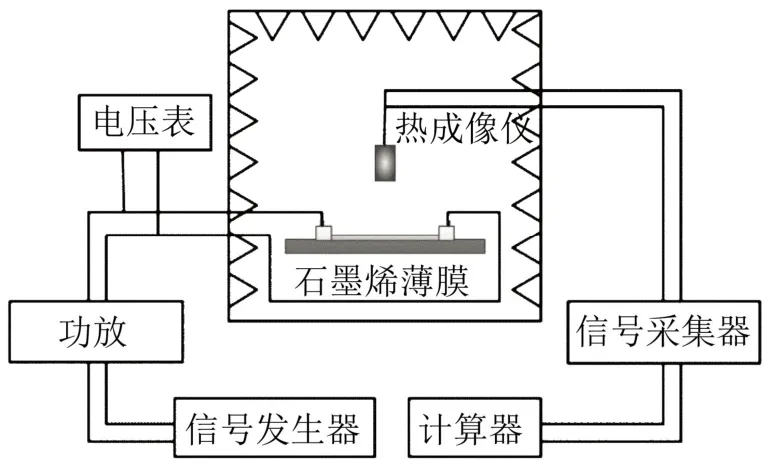
图14 传热实验设计示意图Fig.14 Schematic diagram of heat transfer experiment design

图15 石墨烯薄膜实物图Fig.15 Picture of graphene film

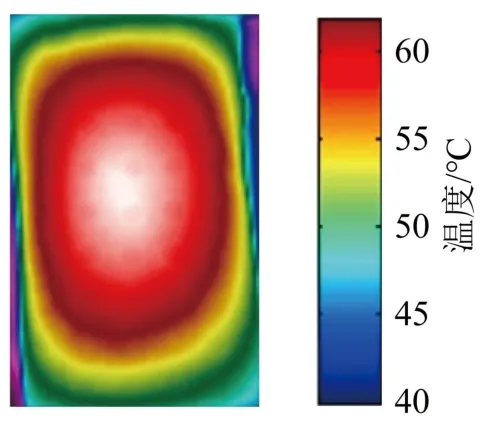
图16 石墨烯薄膜的表面温度分布Fig.16 Surface temperature distribution of graphene film

4.2 声压测试

声学实验设计如图17所示。薄膜产生的声音信号由传声器接收，然后传送到动态信号分析仪。现场测试如图18所示。测点位于薄膜的中轴线上距离薄膜1、2 cm和偏中轴线45°距离薄膜中心点2 cm处。当薄膜的有效输入功率为0.73 W时，测试薄膜声压随频率的变化如图19（a）、19（b）和 19（c）所示。将声压的一维近似解析解和三维数值计算结果列入图19中进行对比，发现三维数值解比一维近似解析解更接近实验值。

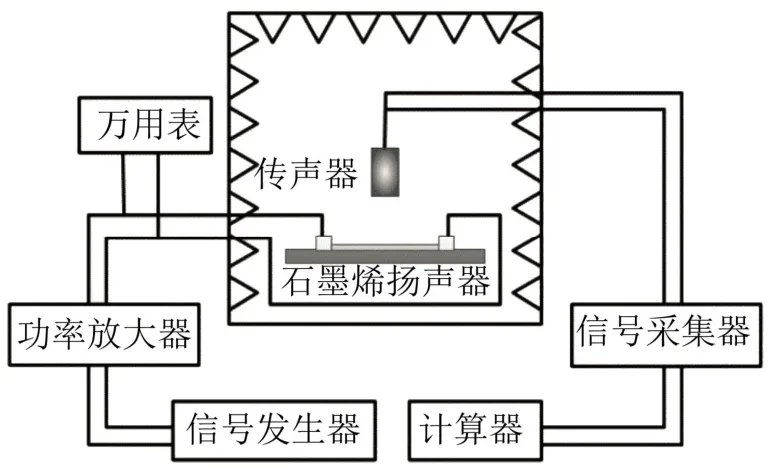
图17 声学实验设计示意图Fig.17 Schematic diagram of acoustic experiment design

图18 测试现场照片Fig.18 Picture of test field

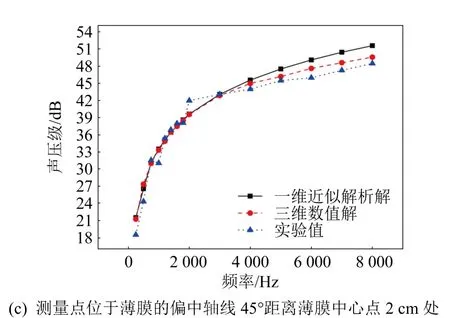
图19 在不同测量点的声压级与频率的关系Fig.19 Relationships between sound pressure level and frequency at different measuring points

5 结 论

从通电石墨烯薄膜的热声效应出发，建立了薄膜的三维热传导模型和三维声扩散模型，计算了薄膜表面的稳态温度分布、温度振荡幅值和声压值，并进行了实验论证，得到以下结论：

（1） 薄膜表面稳态温度分布特点是中央最高，沿四周下降。温度振荡幅值随频率增加而减小。

（2） 声压等压线在靠近声源的地方曲率较小，距离声源越远曲率越大，最后趋近于球面波。声压值随着频率的增加而增加。

（3） 基底的密度、恒压热容和导热系数与石墨烯薄膜的声压级呈负相关。气体的密度和导热系数与石墨烯薄膜的声压级呈正相关，气体的恒压热容与石墨烯的声压级呈负相关。

（4） 将三维模型数值计算的声压值与一维近似解析解及实验值进行对比，三维数值计算结果更加接近实验值，且能计算出声压在空间的连续分布。