零阶Bessel 驻波场中任意粒子声辐射力和力矩的Born 近似*
臧雨宸 苏畅3)† 吴鹏飞3) 林伟军3)
1) (中国科学院声学研究所,北京 100190)
2) (中国科学院大学,北京 100049)
3) (北京市海洋深部钻探测量工程技术研究中心,北京 100190)
声辐射力和声辐射力矩的计算是实现粒子精准操控的重要基础.基于经典声散射理论的偏波级数展开法较难直接用于复杂模型的研究,而纯数值的方法则不利于进行系统的参数化分析.基于Born 近似的基本原理,推导了低频情况下零阶Bessel 驻波场中心任意粒子的声辐射力和力矩表达式.在此基础上,以球形粒子、椭球形粒子和柱形粒子为例进行详细地计算,并考虑声参数的非均匀性对声辐射力和力矩的影响.仿真结果表明,在低频范围内Born 近似具有很高的精度,随着频率的增加和粒子与流体的阻抗匹配变差,Born 近似的精度逐渐下降.对于倾斜放置于零阶Bessel 驻波场中的椭球形粒子和柱形粒子,非对称性会导致其受到声辐射力矩的作用.在粒子尺寸远小于波长的情况下,声辐射力特性与粒子的具体形状几乎无关,但声辐射力矩不然.最后,引入周围流体的黏滞效应并对声辐射力的表达式进行了修正.该研究预期可以为生物医学、材料科学等领域利用驻波场声镊子实现微小粒子的精准操控提供一定的理论指导.
1 引言
当声波在障碍物表面发生反射、散射、折射等物理效应时,会对物体产生力或力矩的作用,分别称为声辐射力和声辐射力矩.基于声辐射力和力矩的粒子精准操控技术在声镊子[1−6]、声悬浮[7,8]等领域展现出巨大的应用前景,同时也对各种情况下声辐射力和力矩的理论计算提出了更高的要求.传统的声辐射力和力矩研究主要基于经典的声散射理论,利用偏波级数展开法求解散射系数进而计算声辐射力和力矩,这一方法可以给出无穷级数形式的解析解,并在刚性球、刚性柱、弹性球、弹性柱等简单模型中得到了成功运用[9−18].对于同心球壳、柱壳等简单的非均匀粒子,偏波级数展开法依然适用,Hasegawa 等[19]和Mitri[20,21]最早给出了这一类问题的解析解,并详细讨论了球壳厚度和材料对声辐射力的影响.Wang 等[22]计算了三层同心可压缩球的声辐射力从而来模拟对生物细胞的操控,随后Peng 等[23,24]将其拓宽到聚焦声束和声表面波入射的情况.Gauss 驻波场、Bessel 驻波场等新型声场对多层弹性球的声辐射力特性也陆续为学者所研究[25−27].近年来,Mitri[28,29]还将该方法与柱函数的加法公式结合,成功研究了偏心柱的声辐射力和力矩特性.在实验探究方面,Mitri[30]通过实验验证了弹性柱在平面行波场中的解析解.Aglyamov等[31]使用1.5 MHz 的单阵元换能器对刚性小球施加声辐射力并观测小球的运动,其实验测量结果和理论预测的结果符合得很好.Nikolaeva 等[32]通过实验探究了倾斜入射的超声束对声吸收散射体的辐射力.Garbin 等[33]对盘状粒子在声辐射力和力矩作用下产生的声电泳现象进行了详细的数值和实验研究,其结果为红细胞等各种盘状粒子的声操控具有指导意义.Johnson 等[34]针对黏滞效应对平面行波场中声辐射力的影响进行了实验测量,并与已有的理论进行对比,结果显示即使对于弱黏性流体,黏滞效应对声辐射力的影响也十分显著.Qiao等[35]对自由空间中球形粒子在黏性流体中的声辐射力进行了理论和实验研究,详细讨论了声压振幅、声场频率和流体黏度对辐射力的影响.
尽管如此,当粒子的形状或结构更加复杂时,散射系数的解析计算变得较为困难甚至根本无法实现,此时有必要借助一些纯数值的方法来进行求解.Wijaya 和Kim[36]利用边界元方法成功研究了非球形粒子在驻波场中的声辐射力和力矩,并以椭球体等形状为例进行了计算.Glynne-Jones 等[37]则借助有限元方法分析了任意形状的弹性和流体微粒的声辐射力.诚然,数值方法的运用大大丰富了声辐射力的研究模型,然而与解析方法相比,数值方法的计算量急剧增加,并且很难根据得到的结果进行模型的参数化分析.幸运的是,在某些情况下,寻求复杂模型的解析解或近似解是可能的.Wei 等[38]给出了声场垂直入射时无限长椭圆柱在长波近似下的声辐射力表达式,Hasheminejad 等[39]利用椭圆坐标系中的马丢函数给出了适用于所有频率范围的结果.Marston[40]给出了低频近似下长椭球与扁椭球在驻波场中的渐近表达式,其中要求椭球体的对称轴与声轴完全重合.Mitri[41−45]则沿用圆柱坐标系和球坐标系下的偏波级数展开法,借助广义Fourier 级数展开理论和数值积分方法,利用半解析的方法成功计算了椭圆柱和椭球体的声辐射力和力矩,其中要求椭圆柱和椭球的长短轴之比不能过大.Silva 等[46]研究了低频近似下任意声场中的椭球形粒子受到的声辐射力矩,并以平面波为例进行了详细分析.Jerome 等[47,48]则直接借助于椭球坐标系计算了可压缩椭球体的声辐射力和力矩.
Bessel 波束作为一类典型的非衍射波束,在光学和声学领域都受到了广泛关注.Marston[49,50]和Mitri[51−55]最早对Bessel 声束的辐射力特性进行了详细研究,特别关注了其产生的负向声辐射力现象.对于高阶Bessel 声束而言,其携带的轨道角动量还可以对物体施加声辐射力矩作用,Zhang 等[56−59],Gong 等[60]系统总结了这一方面的理论框架,并对Bessel 声束声辐射力矩的反转现象进行了理论分析.近年来,Jerome 等[61−63]借鉴量子力学中的Born 近似方法避开了求解散射系数的繁复过程,直接利用曲面积分推导了平面驻波场作用下任意粒子的声辐射力和力矩,并与精确解相比较,结果显示在低频范围内两者符合得很好.本文将Born近似方法拓展到Bessel 驻波场入射的情形,推导得到了零阶Bessel 驻波场中任意粒子声辐射力和力矩的一般积分表达式.在此基础上,以球形粒子、椭球形粒子和柱形粒子为例进行了详细分析,并考虑了粒子密度与声速分布的非均匀性.此外,我们还引入背景流体的黏度,分析其对声辐射力的影响.有必要指出,Born 近似方法的使用存在两个前提条件:1)粒子的密度和声速与周围流体相差不能太大,2)是粒子处在低频驻波场中.
2 声辐射力和力矩的Born 近似
2.1 声辐射力的一般表达式
考虑位于理想流体中的一半径为R的球形粒子,以球心为原点建立球坐标系(r,θ,φ).根据波动方程和级数展开理论,任意的单频入射声场都可以展开为无穷级数的形式:

式中,p0是入射声压的复振幅,k=ω/c0是声波在流体中的波数,ω和c0分别是声波的角频率和流体中的纵波声速,jn和Ynm分别是n阶球Bessel函数和n阶球谐函数,anm是入射声波的波束展开因子.为了简便,我们略去了时间简谐因子 e−iωt.当入射声场与周向角φ无关时,(1)式可以进一步简化为单重求和的级数:

式中,Pn是n阶Legendre 函数,an是入射声波的波束展开因子.散射声场同样也可以表示为级数展开的形式:


式中,ρ0是流体的密度,φinc和φsca分别是入射声场和散射声场对应的速度势函数,Re 表示对物理量取实部,S是将粒子包围在内的一个大封闭球面.将(2)式和(3)式带入(4)式中,可以得到沿z方向的声辐射力表达式:

有必要指出,这一表达式是声辐射力的精确解,且适用于任意频率的入射声波.尽管如此,散射系数的求解通常是较为繁复的过程,因此有必要寻求进一步的化简方法.
2.2 低频驻波场声辐射力的Born 近似
低频驻波场是实际声操控中的常见声场,所谓低频即满足kR<1.低频近似下,只需要考虑单极(n=0)和偶极(n=1)散射项即可,其余散射项均可以忽略.单极和偶极散射项对应的散射系数分别可以近似为[64−66]

式 中,ρm(r) 和cm(r) 分 别是粒 子的密 度与纵 波声速.对于均匀粒子而言,其密度与声速处处相等,因而f1(r) 和f2(r) 是与空间位置无关的常数;对于非均匀介质而言,f1(r) 和f2(r) 则是与空间位置有关的函数.将(6)式代入(5)式可以得到声辐射力的低频近似表达式为

考虑到球形粒子的体积为 4 πR3/3,(8)式可以进一步改写为

当粒子的半径很小时,球形粒子将退化为体积微元,(9)式变为该体积微元受到的声辐射力:
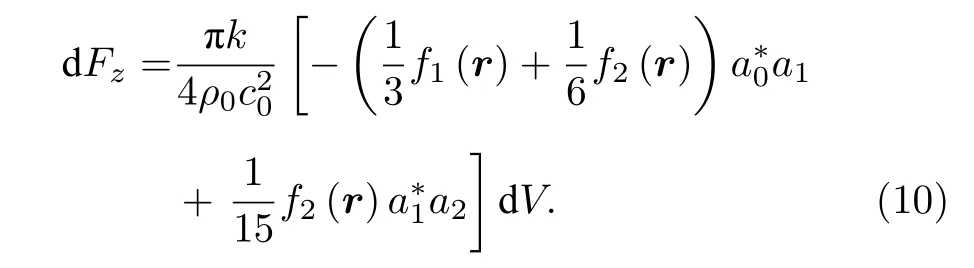
该式反映了声辐射力和体积之间存在的线性关系,因而任意形状粒子的声辐射力都可以直接通过(10)式对作体积分得到,这也正是Born 近似方法的核心思想.需要注意的是,单个体积微元的散射声场同样会产生对其他体积微元的辐射力,因此严格而言通过直接对(10)式作体积分来计算声辐射力是不准确的.因此,Born 近似方法仅适用于粒子的密度和声速与周围流体比较接近的情况,此时散射声场的能量远小于入射声场,从而可以忽略不计.根据(7)式可以看出,此时 |f1(r)| 和 |f2(r)| 均远小于1.对于生物体内的细胞与组织,这一条件是容易满足的.
还有必要指出,Born 近似仅适用于驻波场中声辐射力和声辐射力矩的计算,对于行波场是不能运用的,这是由于行波场中体积微元的声辐射力正比于dV的平方,从而不满足线性叠加原理.事实上,驻波场与行波场产生声辐射力的机理并不相同.前者不携带声能流,其辐射力效应是由声场动能和势能的空间梯度引起;后者则携带声能流,其辐射力效应则反映了声波与物体之间的动量和能量传递.
以上主要针对声辐射力进行了讨论,声辐射力矩的计算是类似的,只需将径矢与其作矢量积运算即可.
2.3 零阶Bessel 驻波场作用下的Born 近似
考虑位于零阶Bessel 驻波场中的任意粒子.为了讨论的方便,我们假定零阶Bessel 驻波场的声轴沿z方向且粒子恰好固定于声束中心(坐标原点),此时声压可以表示为[67]

式 中,Jn是n阶 柱Bessel 函 数,kr=ksinβ和kz=kcosβ分别是径向和轴向的波矢分量,β是Bessel 声束的半锥角,h是粒子中心到距离其最近的声压波节的距离.容易看出,当β=0 时,(11)式将退化为平面驻波场的表达式.(11)式与周向角无关,当然可以展开为(2)式的形式,其中的波束展开因子为[49]

将(12)式代入(10)式可以得到零阶Bessel驻波场对体积微元的声辐射力:

有必要指出,尽管我们只给出了轴向声辐射力的结果,这并不意味着横向声辐射力 (Fx,Fy) 为零.但根据文献[54]的结论,当满足Born 近似的条件时,横向声辐射力比轴向声辐射力小至少两个数量级,因此只考虑轴向分量是合理的.
根据式(15),很容易通过矢量积运算得到粒子所受声辐射力矩的表达式:
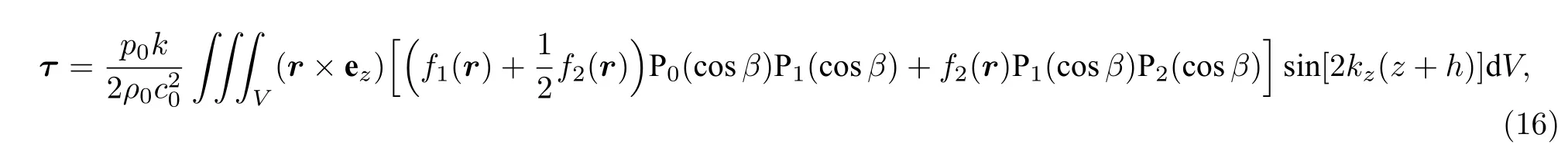
式中ez是z方向的单位矢量.
至此,在已知粒子形状和密度与声速空间分布的前提下,原则上可以根据(15)式和(16)式求得任意粒子声辐射力和力矩的Born 近似解.对于密度与声速均匀分布的粒子而言,(15)式和(16)式中的f1(r) 和f2(r)是与径矢无关的常数,因而与之有关的项可以提到积分号外,此时声辐射力和力矩的表达式简化为:
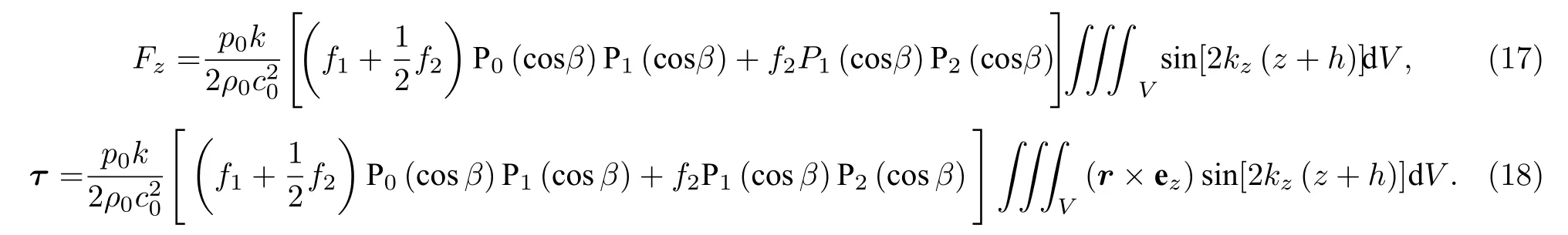
对于密度与声速均轴对称分布的粒子,(15)式和(16)式亦可以进一步简化.如图1 所示,假定粒子的对称轴位于xOz平面内,其对称轴为z’轴,且与z轴所夹的角度为θs,以O为原点再建立一柱坐标系(ρ′,φ′,z′),两坐标系之间存在以下关系:
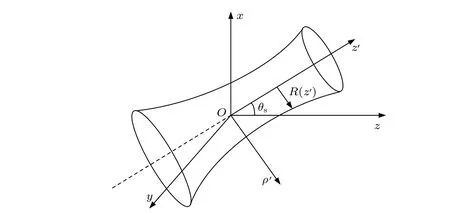
图1 倾斜放置于零阶Bessel 驻波场中心的任意轴对称粒子Fig.1.An arbitrary object with axisymmetric geometry obliquely positioned in a zero-order standing Bessel beam.

(22)式和(23)式中对于角度的积分可以直接利用柱Bessel 函数的性质得到解析解,于是声辐射力和力矩的表达式分别简化为:

式中J1表示一阶柱Bessel 函数.进一步地,如果粒子的非均匀性仅仅在z’方向体现,即f1(r) 和f2(r) 仅仅是z′的函数,则(24)式和(25)式中关于极径的积分可以直接进行计算,最终两式变为如下的单重积分:
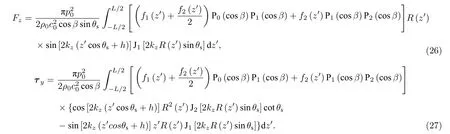
当粒子尺寸远小于声波波长时(kR(z′)≪1,kL ≪1),还可以利用柱Bessel 函数的小宗量近似对(26)式和(27)式再次进行化简,此时声辐射力和力矩的近似表达式为:

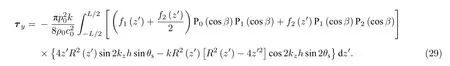
3 球形粒子的Born 近似
3.1 均匀球形粒子

式中V=4πR3/3是球形粒子的体积.(31)式给出了声辐射力矩为零的结果,对于均匀分布的球形粒子,这是可以预料的.
(30)式是通过Born 近似得到的结果,其精确性可以通过声辐射力的精确表达式(5)式进行检验.为了方便比较,我们对(5)式和(30)式均用进行归一化处理,这里S0=πR2是球形粒子的散射截面.图2 同时给出了利用(30)式和(5)式对零阶Bessel 驻波场作用下水中均匀球形粒子受到的归一化声辐射力的计算结果,水的密度ρ0=1000 kg/m3,声速c0=1480 m/s ,β=π/6,kzh=π/4.假定粒子的密度与水相同,图2(a),(b)和(c)分别对应着cm/c0=1.01 ,cm/c0=1.05和cm/c0=1.1 的情况.结果显示,粒子受到的声辐射力均可正可负,在kR<1 的低频范围内,Born近似的结果与精确解符合得很好,随着kR的增加,Born 近似解的误差开始增大.这是由于在中高频范围内,四极散射项(n=2)、八极散射项(n=3)等的影响不能忽略,同时这也再次验证了Born 近似仅适用于kR<1 的低频范围.尽管如此,Born近似解和精确解在中高频范围内的变化趋势基本保持一致,且声辐射力和力矩极值所对应的kR基本不变.因此,在精度要求不是很高的情况下,Born近似方法可以为实际的声操控提供一定的理论指导.此外,粒子与周围流体的声速相差越大,Born近似解和精确解的差异也越大.随着两者声参数差异的增加,散射声场对声辐射力的贡献不能再忽略,从而导致Born 近似方法误差的增大.
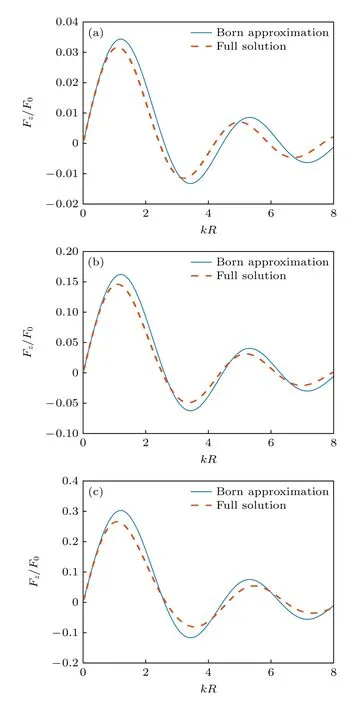
图2 零阶Bessel 驻波场中心均匀球形粒子受到的归一化声辐射力随kR 的变化(β=π/6,kzh=π/4,ρm/ρ0=1)(a) cm/c0=1.01;(b) cm/c0=1.05;(c) cm/c0=1.1Fig.2.The dimensionless acoustic radiation force plots for a homogeneous sphere versus kR in a zero-order standing Bessel beam (β=π/6,kzh=π/4,ρm/ρ0=1):(a) cm/c0=1.01;(b) cm/c0=1.05;(c) cm/c0=1.1.
图3 给出了kR=0.5 时均匀球形粒子的归一化声辐射力随声束半锥角β的变化关系,粒子声参数的设置与图2 完全相同.容易看出,随着粒子与周围流体声参数差异的增加,两者的阻抗匹配变差,声辐射力也随之出现明显的增强.此外,半锥角的增加均会导致声辐射力明显减小,当β=0 时,结果将退化为平面驻波场入射的情形.

图3 零阶Bessel 驻波场中心均匀球形粒子受到的归一化声辐射力随β 的变化(kR=0.5,kzh=π/4,ρm/ρ0=1)Fig.3.The dimensionless acoustic radiation force plots for a homogeneous sphere versus β in a zero-order standing Bessel beam (kR=0.5,kzh=π/4,ρm/ρ0=1).
进一步考虑kR ≪1 的情况.我们当然可以利用(28)式计算此时的声辐射力,但直接计算(30)式在kR ≪1 时的极限是更为简便的方法.此时声辐射力的公式简化为:

3.2 非均匀球形粒子
实际的声操控中粒子往往是非均匀的,即f1(r)和f2(r) 是空间位置的函数.考虑粒子密度和声速仅仅随径向坐标r变化的情形,并满足如下的关系:
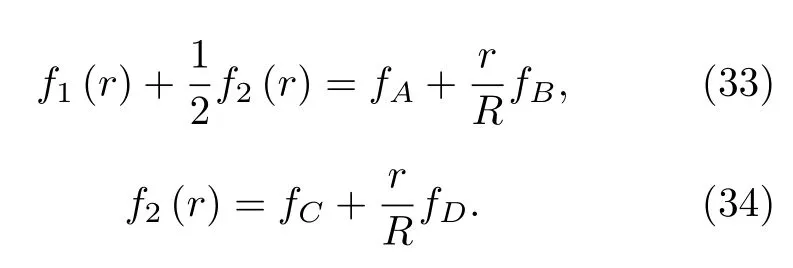
容易看出,f1(r)+f2(r)/2 和f2(r) 在球心处分别为fA和fC,在球形粒子表面分别为fA+fB和fC+fD,并且随径向坐标线性变化.将(33)式和(34)式代入(15)式和(16)式,通过在球坐标中作体积分可以得到声辐射力和力矩的表达式:
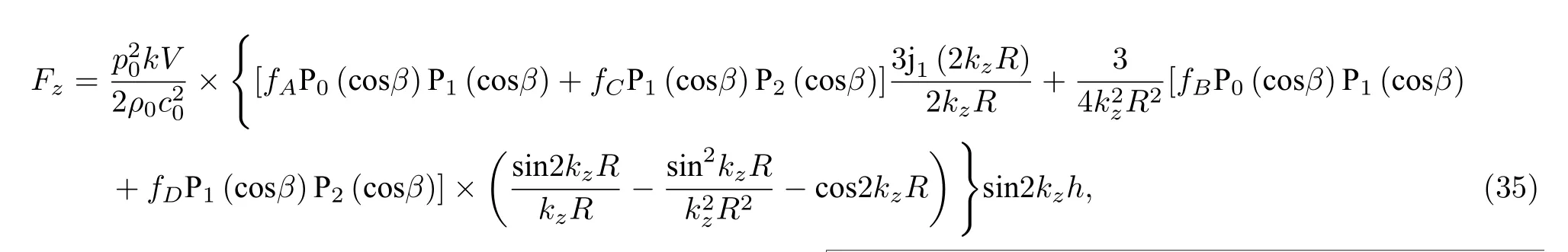

显然,当fB=fD=0 时,(35)式将退化为均匀球形粒子的结果(30)式.此外,尽管此时粒子存在非均匀性,但对称性使其仍然不受到声辐射力矩的作用.
利用(35)式对水中非均匀球形粒子的声辐射力进行分析.假设球心处的密度和声速与水完全相同,此时显然有fA=fC=0.图3 计算了归一化声辐射力随kR的变化关系,其中β=π/6 ,kzh=π/4.粒子表面的声速和密度分别设置为四种情形:1420 kg/m3和940 m/s,1460 kg/m3和980 m/s,1500 kg/m3和1020 m/s,1540 kg/m3和1060 m/s.一般而言,密度越大的介质声速越大,因此这样的设置具有一定的合理性.经计算,在这4 种情况下分别有:fB=−0.250,fD=−0.042 ;fB=−0.077,fD=−0.014 ;fB=0.071,fD=0.013 ;fB=0.197,fD=0.039.结果显示,粒子的声参数与周围流体相差越大,声辐射力的峰值也越大,但声辐射力峰值所对应的kR值几乎保持不变.有必要指出,这是因为在Born 近似的过程中忽略了散射波对声辐射力的贡献.事实上,声参数的改变必然会改变粒子的本征振动模式,进而影响声辐射力峰值的位置.另一方面,如前所述,Born 近似解仅在kR<1时保持较高的精度,中高频范围内的结果参考意义有限.基于这一考虑,图5 给出了kR=0.5 时归一化声辐射力随半锥角的变化曲线,粒子声参数的设置与图4 完全相同.不难看出,随着声束半锥角的增加,声辐射力的幅值明显减小并最终趋于零.当β=0时声辐射力的幅值最大,此时正对应着平面驻波场入射的情况.
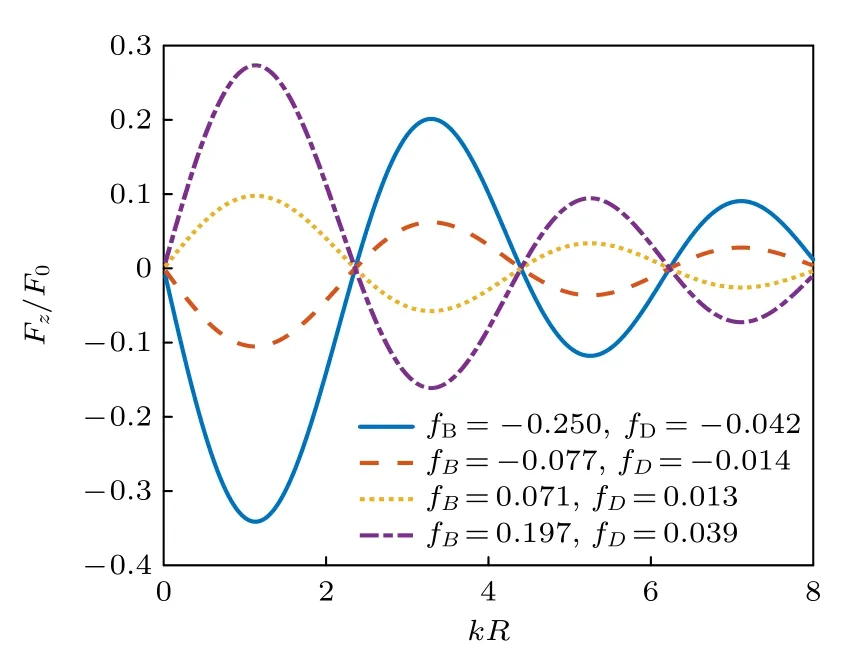
图4 零阶Bessel 驻波场中心非均匀球形粒子受到的归一化声辐射力随kR 的变化(fA=fC=0,β=π/6,kzh=π/4)Fig.4.The dimensionless acoustic radiation force plots for an inhomogeneous sphere versus kR in a zero-order standing Bessel beam (fA=fC=0,β=π/6,kzh=π/4).

图5 零阶Bessel 驻波场中心非均匀球形粒子受到的归一化声辐射力随β 的变化(fA=fC=0,kR=0.5,kzh=π/4)Fig.5.The dimensionless acoustic radiation force plots for an inhomogeneous sphere versus β in a zero-order standing Bessel beam (fA=fC=0,kR=0.5,kzh=π/4).
同样地,(35)式在kR ≪1 的情况下还可以作进一步近似,其取极限的结果为

与(32)式类似,(37)式归一化后的结果同样与kR成正比(固定kzh).注意到当fB=fD=0 时,粒子将不存在非均匀性,(37)式将退化为(32)式.
从以上过程可以看出,对于由(33)式和(34)式表示的声参数分布,声辐射力的积分式是可以解析求解的,但对于更复杂分布的非均匀球形粒子,可能需要通过数值积分方法进行求解.
4 椭球形粒子的Born 近似
4.1 均匀椭球形粒子
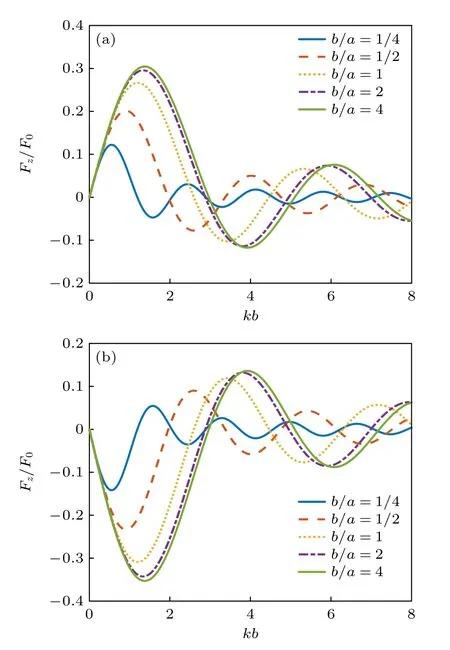
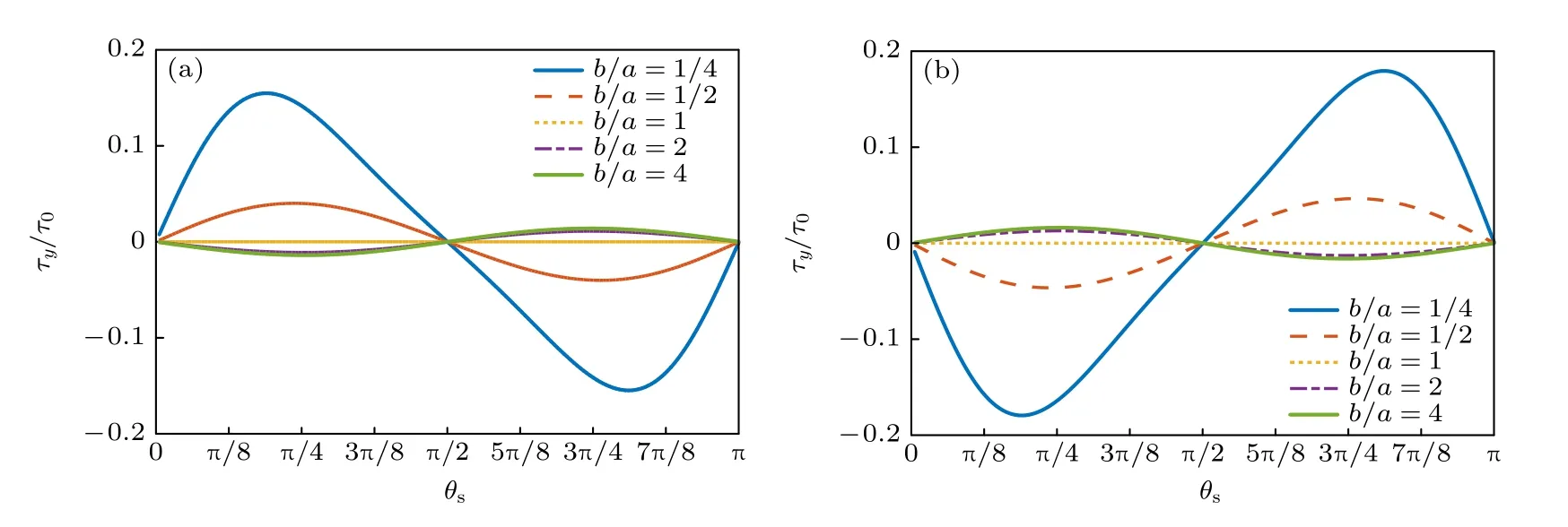
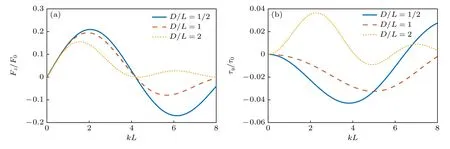
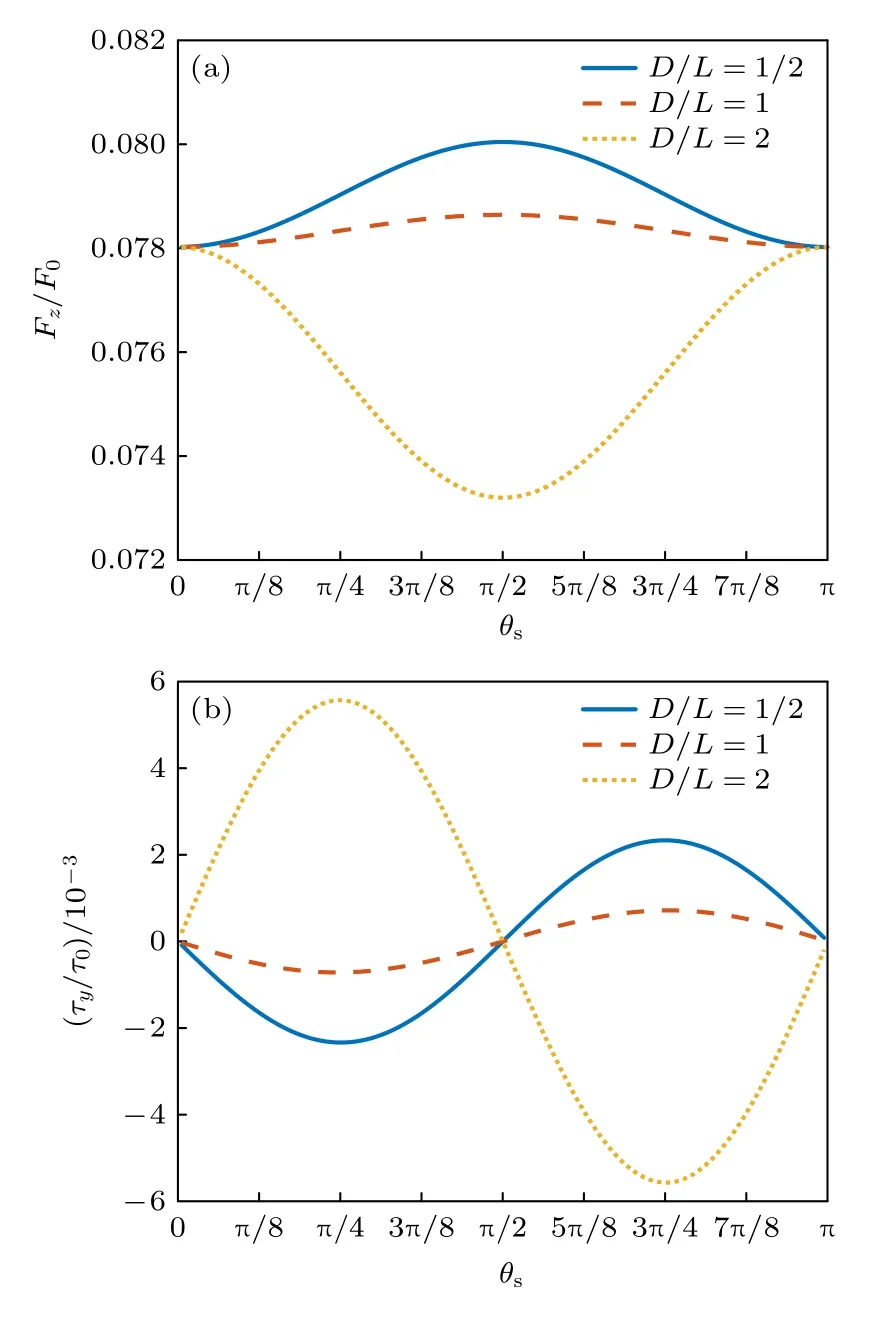
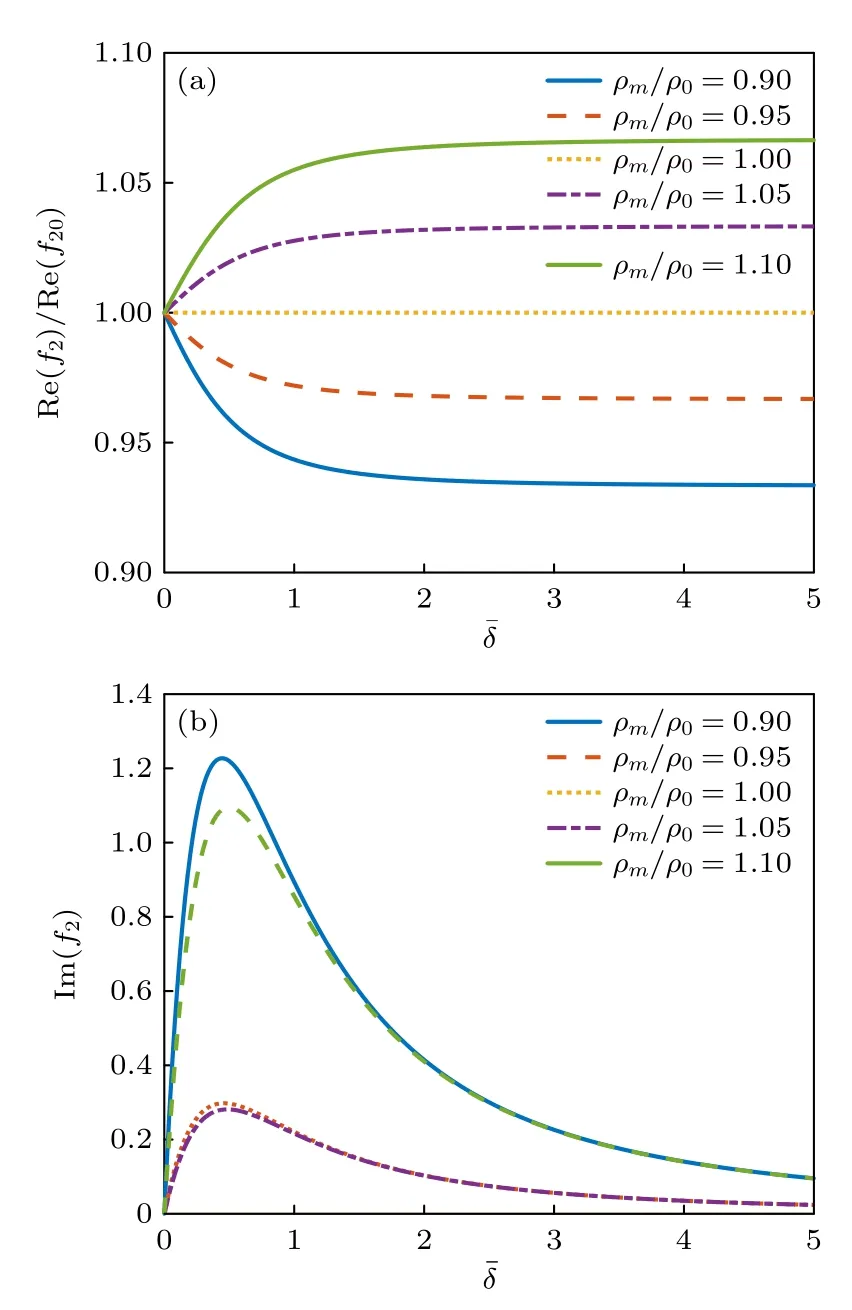
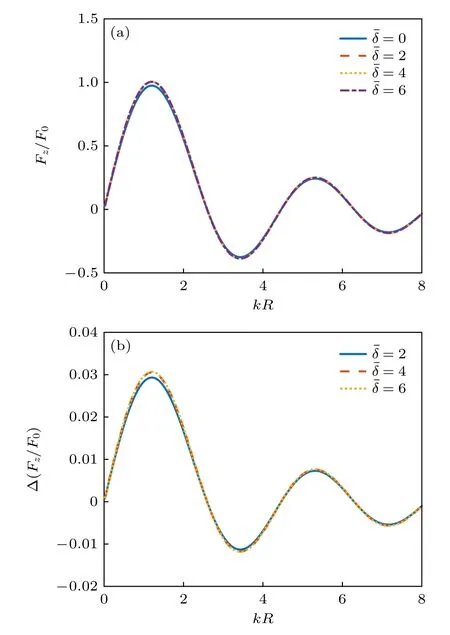
椭球形粒子在实际的声操控中也十分常见,如驻波场中的悬浮液滴在声辐射力、重力和表面张力的耦合作用下通常呈现为椭球的形状[8].考虑位于零阶Bessel 驻波场中心的均匀椭球形粒子,其在对称轴z’方向的半轴长度为b,垂直于对称轴方向的横截圆面的最大半径为a,显然a>b对应着扁椭球的情形,a 对于均匀椭球形粒子而言,其声辐射力和力矩的积分表达式(17)式和(18)式都没有显式的解析结果,只能通过数值积分方法来进行计算.图5 给出了零阶Bessel 驻波场中心均匀椭球形粒子的归一化声辐射力和力矩随kb的变化曲线,其中声束的半锥角β=π/6 ,对称轴的取向角θs=π/6,粒子的纵横比分别为1/4,1/2,1,2 和4.粒子与水的密度和声速之比分别为ρm/ρ0=1,cm/c0=1.05.与声辐射力相对应,声辐射力矩的归一化因子为τ0=bF0.需要注意的是,在计算声辐射力时设置kzh=π/4,计算声辐射力矩时则设置kzh=0,这是为了让粒子的声辐射力和力矩效应均最为显著.从图6(a)不难看出,当增加粒子的纵横比时,声辐射力的峰值也随之增加,且峰值所对应的kb值也随之改变.尽管如此,所有曲线在kb ≪1 的低频范围内几乎完全重合,这说明在粒子尺寸远小于波长时,声辐射力特性与粒子的具体形状几乎无关.从图6(b)可以发现,当粒子的对称轴与声轴既不平行也不垂直时,椭球形粒子会受到不为零的声辐射力矩作用,且其方向会随着kb的变化而变化,这预示着从y′轴正向看去,粒子既可以逆时针转动也可以顺时针转动.当纵横比为1 时,粒子将退化为球形,因而不存在声辐射力矩.同时,椭球形粒子偏离球形的程度越大,声辐射力矩的峰值也越大.注意到即使是在kb ≪1 的范围内,粒子纵横比对声辐射力矩特性的影响也十分显著,这与声辐射力的情形有所不同. 图6 零阶Bessel 驻波场中心均匀椭球形粒子受到的归一化声辐射力和力矩随kb 的变化(β=π/6,θs=π/6,ρm/ρ0=1,cm/c0=1.05) (a)归一化声辐射力(kzh=π/4);(b)归一化声辐射力矩(kzh=0)Fig.6.The dimensionless acoustic radiation force and torque plots for a homogeneous spheroid versus kb in a zeroorder standing Bessel beam (β=π/6,θs=π/6,ρm/ρ0=1,cm/c0=1.05):(a) Dimensionless acoustic radiation force(kzh=π/4);(b) dimensionless acoustic radiation torque(kzh=0). 图7(a)和图7(b)分别给出了kb=0.5 时归一化声辐射力和力矩随粒子对称轴取向角的变化关系,其余参数设置与图6 完全相同.从仿真结果可以看出,椭球形粒子的声辐射力关于θs=π/2 呈偶对称,这是由模型的对称性决定的.在θs=π/2 处,长椭球形粒子的声辐射力达到最大值,而扁椭球形粒子的声辐射力达到最小值.对于球形粒子而言,声辐射力曲线退化为与θs无关的一条水平直线.与声辐射力的结果不同,椭球形粒子的声辐射力矩关于θs=π/2 呈奇对称,在θs=0,π/2,π 处力矩均恒为零,这也是模型对称性所要求的必然结果.在0<θs<π/2的范围内,长椭球形粒子的声辐射力矩取负值,扁椭球形粒子的声辐射力取正值,在π/2<θs<π的范围内则恰好相反.此外,球形粒子的声辐射力矩恒为零,这是与预期相符的. 图7 零阶Bessel 驻波场中心均匀椭球形粒子受到的归一化声辐射力和力矩随θs 的变化(kb=0.5,β=π/6,ρm/ρ0=1,cm/c0=1.05) (a)归一化声辐射力(kzh=π/4);(b)归一化声辐射力矩(kzh=0)Fig.7.The dimensionless acoustic radiation force and torque plots for a homogeneous spheroid versus θs in a zeroorder standing Bessel beam (kb=0.5,β=π/6,ρm/ρ0=1,cm/c0=1.05):(a) Dimensionless acoustic radiation force(kzh=π/4);(b) dimensionless acoustic radiation torque(kzh=0). 在kb ≪1 的条件下,可以利用(28)式和(29)式来计算此时声辐射力和力矩的近似表达式: 式中V=4πa2b/3 是椭球形粒子的体积.(38)式形式上与(32)式完全相同,这再次验证了在粒子尺寸远小于波长的情况下,声辐射力特性与粒子的具体形状和粒子对称轴的取向角θs均无关.(39)式在一般情况下是非零的,且依赖于粒子对称轴的取向角θs,当粒子的对称轴与声轴平行或垂直时力矩为零.容易看出,当a=b时声辐射力矩也将消失,这是因为此时粒子退化为球形.有必要指出,在固定kzh的条件下,归一化后的声辐射力矩并非与kb成正比,而是与成正比,这与声辐射力的情形有所不同. 尝试将非均匀性引入椭球形粒子.考虑粒子的密度和声速仅仅随z′坐标变化的情形,并满足如下的关系: 由于此时的非均匀性仅仅体现在z′坐标上,因此可以通过(26)式和(27)式对椭球形粒子的声辐射力和力矩进行计算.与均匀椭球形粒子的情况类似,此时仍然无法得到积分的解析结果,需要进行数值积分运算.图8 计算了零阶Bessel 驻波场中心非均匀椭球形粒子的归一化声辐射力随kb的变化关系,图8(a)中的椭球形粒子在z′=−L/2 处ρm=1000 kg/m3,cm=1480 m/s,在z′=L/2 处ρm=1080 kg/m3,cm=1560 m/s,图8(b)中的椭球形粒子在z′=−L/2 处m=1000 kg/m3,cm=1480 m/s,在z′=L/2 处m=920 kg/m3,cm=1400 m/s,经 计算在这两种情况下分别有:fA=0.137,fB=0.254,fC=0.026,fD=0.051 ;fA=−0.160,fB=−0.349,fC=−0.027,fD=−0.056,其余参数设置与图6完全相同.结果显示,图8(a)的变化规律与图6(a)基本一致,但声辐射力的幅值更大.图8(b)的仿真结果则与图8(a)异号,这是由于此时粒子的声阻抗小于周围流体.图9 给出了与图8 相同情况下归一化声辐射力矩的计算结果,其中图9(a)和图6(b)的变化规律几乎一致,而图9(b)则与图9(a)异号. 图8 零阶Bessel 驻波场中心非均匀椭球形粒子受到的归一化声辐射力随kb 的变化(β=π/6,θs=π/6,kzh=π/4):(a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056Fig.8.The dimensionless acoustic radiation force plots for an inhomogeneous spheroid versus kb in a zero-order standing Bessel beam (β=π/6,θs=π/6,kzh=π/4):(a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056. 图9 零阶Bessel 驻波场中心非均匀椭球形粒子受到的归一化声辐射力矩随kb 的变化(β=π/6,θs=π/6,kzh=0) (a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056Fig.9.The dimensionless acoustic radiation torque plots for an inhomogeneous spheroid versus kb in a zero-order standing Bessel beam (β=π/6,θs=π/6,kzh=0):(a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056. 图10 和图11 给出了kb=0.5 时归一化声辐射力和力矩随粒子对称轴取向角的变化关系,其余参数的设置与图8 和图9 完全相同.同样地,图10(a)和图11(a)的计算结果与图7(a)和图7(b) 完全类似,图10(b)和图11(b)的结果则分别与图10(a)和图11(a)异号. 图10 零阶Bessel 驻波场中心非均匀椭球形粒子受到的归一化声辐射力随θs 的变化(kb=0.5,β=π/6,kzh=π/4)(a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056Fig.10.The dimensionless acoustic radiation force plots for an inhomogeneous spheroid versus θs in a zero-order standing Bessel beam (kb=0.5,β=π/6,kzh=π/4):(a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056. 图11 零阶Bessel 驻波场中心非均匀椭球形粒子受到的归一化声辐射力矩随θs 的变化(kb=0.5,β=π/6,kzh=0) (a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056Fig.11.The dimensionless acoustic radiation torque plots for an inhomogeneous spheroid versus θs in a zero-order standing Bessel beam (kb=0.5,β=π/6,kzh=0):(a) fA=0.137,fB=0.254,fC=0.026,fD=0.051;(b) fA=–0.160,fB=–0.349,fC=–0.027,fD=–0.056. 考察kb ≪1 且纵横比b/a ≫1 的情况.利用(28)式和(29)式得到此时声辐射力和力矩的近似表达式: 可以看出,声辐射力和力矩均与粒子对称轴的取向角有关.若fB和fD均取正值,则当θs=0 时粒子的声辐射力最大,当θs=π/2 时粒子的声辐射力最小,但这两种情况下声辐射力矩均由于对称性而消失.考虑到kb ≪1 ,表征粒子声参数非均匀性的fB和fD对声辐射力的贡献远小于粒子声参数的平均值fA和fC,而声辐射力矩的情况则恰好相反.值得注意的是,在固定kzh的前提下,此时的归一化声辐射力和力矩与频率的依赖关系较为复杂,两者不再存在简单的幂次关系.对于均匀椭球形粒子而言,只需置fB=fD=0 即可,此时(42)式退化为(38)式,但(43)式并不退化为(39)式.若给(39)式也加上纵横比b/a ≫1 的前提,则两者完全等价,这也是预期的结果. Born 近似同样也适用于柱形粒子.考虑截面直径为D、长度为L的一均匀柱形粒子,根据几何关系显然有R(z)=D/2,此时(26)式和(27)式存在解析的积分结果,声辐射力和力矩分别为:这里V=(π/4)D2L是柱形粒子的体积.从(45)式可以看出,当柱形粒子的对称轴平行或垂直于声轴时,声辐射力矩将由于对称性消失,这是预料之中的结果. 图12 给出了零阶Bessel 驻波场中心均匀柱形粒子的归一化声辐射力和力矩随kL的变化曲线,其中声束的半锥角β=π/6,对称轴的取向角θs=π/6,D/L分别为1/2,1 和2.粒子与水的密度和声速之比仍然设置为ρm/ρ0=1,cm/c0=1.05.对于柱形粒子,此时声辐射力和声辐射力矩的归一化因子分别为,其中S0=(π/4)D2是柱形粒子的横截面积.同样地,在计算声辐射力时设置kzh=π/4,计算声辐射力矩时则设置kzh=0.结果显示,不同的声辐射力曲线在kL ≪1 的低频范围内几乎完全重合,这同样反映了粒子尺寸远小于波长时声辐射力特性和粒子的具体形状无关,而声辐射力矩则无此性质.声辐射力和力矩的方向均同时受到kL和D/L的影响,可取正值或负值. 图12 零阶Bessel 驻波场中心均匀柱形粒子受到的归一化声辐射力和力矩随kL 的变化(β=π/6,θs=π/6,ρm/ρ0=1,cm/c0=1.05) (a)归一化声辐射力(kzh=π/4);(b)归一化声辐射力矩(kzh=0)Fig.12.The dimensionless acoustic radiation force and torque plots for a homogeneous cylinder versus kL in a zero-order standing Bessel beam (β=π/6,θs=π/6,ρm/ρ0=1,cm/c0=1.05):(a) Dimensionless acoustic radiation force (kzh=π/4);(b) dimensionless acoustic radiation torque (kzh=0). 图13 给出了kL=0.5 时归一化声辐射力和力矩随粒子对称轴取向角的变化关系,其余参数设置与图12 完全相同.与椭球形粒子的结果类似,柱形 粒子的声辐射力 关于θs=π/2 偶对 称,且 在θs=π/2处取得极大值或极小值.声辐射力矩则关于θs=π/2 奇对称,且在θs=0,π/2,π 力矩均由 于对称性消失. 图13 零阶Bessel 驻波场中心均匀柱形粒子受到的归一化声辐射力和力矩随θs 的变化(β=π/6,kL=0.5,ρm/ρ0=1,cm/c0=1.05) (a)归一化声辐射力(kzh=π/4);(b)归一化声辐射力矩(kzh=0)Fig.13.The dimensionless acoustic radiation force and torque plots for a homogeneous cylinder versus θs in a zeroorder standing Bessel beam (β=π/6,kL=0.5,ρm/ρ0=1,cm/c0=1.05):(a) Dimensionless acoustic radiation force (kzh=π/4);(b) dimensionless acoustic radiation torque (kzh=0). 考虑横截面半径和粒子长度均远小于波长的情形(kD ≪1,kL ≪1),此时的声辐射力和力矩可以近似表示为更简洁的形式: (46)式和(32)式形式上完全相同,再次验证了粒子尺寸远小于波长时声辐射力特性和粒子的具体形状无关.(47)式则与D和L均有关.有趣的是,当时,无论对称轴的取向角如何,粒子的声辐射力矩均恒为零,这对于实际声操控中如何保持粒子的力矩平衡有重要的理论指导意义. 尝试在柱形粒子模型中引入非均匀性.同样考虑粒子的密度和声速仅仅随z’坐标变化的情形,并满足(40)式和(41)式所示的线性关系.显然,粒子的声参数仍然随径向坐标呈线性变化,f1(z′)+f2(z′)/2和f2(z′) 在柱形粒子的一端z′=−L/2 分别取值为fA−fB和fC−fD,在另一端z′=L/2 分别取值为fA+fB和fC+fD.将(40)式和(41)式代入(26)式和(27)式可以得到此时声辐射力和力矩的表达式: 根据(48)式和(49)式,可以直接对非均匀柱形粒子的声辐射力和力矩进行仿真,这里不再详细展开. 进一步考察kD ≪1,kL ≪1 且D ≪L的情况,(48)式和(49)式可以近似表示为: 同样地,考虑到kL ≪1,表征粒子非均匀性的参数fB和fD对声辐射力的贡献远小于粒子声参数的平均值fA和fC,而声辐射力矩的情况则恰好相反.对于均匀柱形粒子(fB=fD=0),(50)式将退化为(46)式,(51)但式并不退化为(47)式.类似地,若给(51)式也加上D ≪L的前提条件,则(51)式和(47)式完全一致. 在实际的声操控中,周围流体往往存在一定的黏滞效应,该效应不可避免地会对声辐射力产生一定的影响,因而需要对理想流体中的结果作修正.根据流体力学的基本理论,黏性流体中声波的边界层厚度定义为[68,69] 式中,ν=η/ρ0是流体的动力学黏滞系数,η是流体本身的黏滞系数.对于室温下水中1 kHz 的声波而言,声波的边界层厚度约为0.6 µm.对于半径为R的球形粒子,定义归一化边界层厚度为 根据文献[70]中的讨论,在考虑流体黏滞吸收的情况下,单极散射系数f1(r) 保持不变,偶极散射系数f2(r) 则会变为如下的复杂形式: 一般而言,(54)式是复数量.这里我们考虑两种特殊的情况:对于密度与周围流体相等的粒子,有f1(r)≡0,此时的偶极散射系数与流体的黏滞效应无关.对于粒子尺寸较小且流体黏度较大的情况(≫1),此时的偶极散射系数近似为一个实数量f2(r)≈2[ρm(r)−ρ0(r)]/(3ρ0(r)). 对于均匀球形粒子,(54)式与空间位置无关.图14(a)和图14(b) 分别给出了此时偶极散射系数f2的实部和虚部随归一化边界层厚度的变化曲线,其中粒子与周围流体的密度比分别设置为ρm/ρ0=0.9, 0.95, 1, 1.05, 1.1.为了便于比较,图14(a)中各曲线均作了归一化处理,归一化因子为理想流体(=0)中偶极散射系数的实部(记为 R e(f20)).从图中可以看出,随着粒子密度的增加,R e(f2) 也随之增加.当增加边界层厚度时,R e(f2) 在ρm/ρ0>1时先增加后趋于稳定,而在ρm/ρ0<1 时先减小后趋于稳定.与之有所不同的是,无论粒子的密度如何(ρm/ρ0=1 除外),I m(f2) 均随着边界层厚度的增大先增加而后减小,在≈0.5 时达到最大值.此外,粒子密度与流体密度越接近,I m(f2) 越小. 图14 均匀球形粒子的偶极散射系数f2 随 的变化 (a)Re(f2)/Re(f20) ;(b) Im(f2)Fig.14.The dipole scattering coefficient f2 plots for a homogeneous sphere versus (a)Re(f2)/Re(f20);(b) Im(f2). 接下来考虑对声辐射力的修正.具体地,只需要用 R e(f2(r)) 代 替f2(r) 即可.于是理想流体中任意声场入射下的体积微元受到的声辐射力(10)式变为 对(56)式作体积分即得到黏性流体中球形粒子的声辐射力的一般表达式. 考虑零阶Bessel 驻波场中心的均匀球形粒子,此时需要将理想流体中的结果(30)式修正为 图15(a)计算了不同归一化边界层厚度下水中均匀球形粒子的归一化声辐射力随kR的变化曲线,其中β=π/6,k z h=π/4,粒子与流体的声参数之比为ρm/ρ0=1.2,c m/c0=1.1.为了进一步凸显流体黏滞效应对声辐射力的影响,图15(b)给出了不同归一化边界层厚度下黏性流体中声辐射力和理想流体中归一化声辐射力的差值曲线,其参数设置与图15(a)完全相同.计算结果显示,由于流体黏滞效应的存在,粒子的正向与负向声辐射力均会得到一定的增强,且黏滞效应的影响随声辐射力幅值的增大而增大.当边界层厚度达到数倍波长时,由于 R e(f2(r)) 趋于稳定,声辐射力也不再随边界层厚度的增加而变化.整体而言,流体黏滞效应对声辐射力的影响较为微弱,因而理想流体中的结果不失为很好的近似.必须指出,这一结论是在粒子与流体密度差异不大的前提下得出的,若两者的密度相差明显,黏滞效应的影响可能较为显著,但此时的模型已经不再满足Born 近似的适用条件,故而这里不再详细讨论. 图15 零阶Bessel 驻波场中心均匀球形粒子受到的归一化声辐射力随kR 的变化(β=π/6,kzh=π/4,ρm/ρ0=1.2,cm/c0=1.1) (a) 归一化声辐射力;(b) 黏性流体与理想流体中归一化声辐射力的差值Fig.15.The dimensionless acoustic radiation force plots for a homogeneous sphere versus kR in a zero-order standing Bessel beam (β=π/6,kzh=π/4,ρm/ρ0=1.1,cm/c0=1.1):(a) Dimensionless acoustic radiation force;(b) difference of dimensionless acoustic radiation force in a viscous fluid and in an ideal fluid. 本文将Born 近似方法运用到低频零阶Bessel驻波场中,推导了位于声场中心的任意粒子受到的声辐射力和力矩的积分表达式,并以球形粒子、椭球形粒子和柱形粒子为例进行大量的仿真计算.主要得到如下结论: 1)在kR<1 的低频范围内,Born 近似的结果与精确解符合得很好.随着kR的增加,Born近似解的误差逐渐增大.此外,粒子与周围流体声参数的差异越大,Born 近似解的误差也越大; 2)当椭球形粒子或柱形粒子的对称轴不与声轴平行或垂直时,会产生由于非对称性导致的声辐射力矩作用.椭球形粒子、柱形粒子的声辐射力和力矩关于θs=π/2 分别呈偶对称和奇对称; 3)当粒子的尺寸远小于声波波长时,粒子的具体形状对其声辐射力特性几乎没有影响,而声辐射力矩特性则受到纵横比的显著影响; 4)周围流体的黏滞效应主要通过影响偶极散射系数进而影响声辐射力,当粒子与周围流体密度差异不大时,黏滞效应的影响较为微弱. 有必要再次强调,利用Born 近似的方法求解声辐射力和力矩时必须满足两个前提条件:1)粒子与所处流体介质的声参数相差不能太大;2)粒子所处的声场必须低频驻波场.本文的研究结果提供了一种求解驻波场声辐射力的新思路,可以为实现粒子的精准声操控和无容器处理技术提供必要的理论基础.


4.2 非均匀椭球形粒子



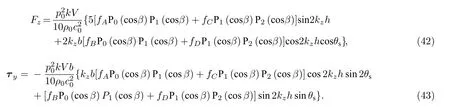
5 柱形粒子的Born 近似
5.1 均匀柱形粒子
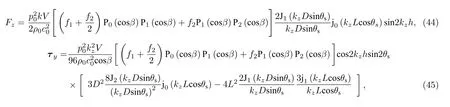

5.2 非均匀柱形粒子

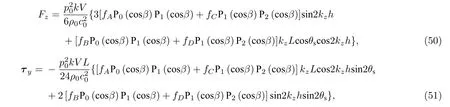
6 周围流体黏滞效应的影响



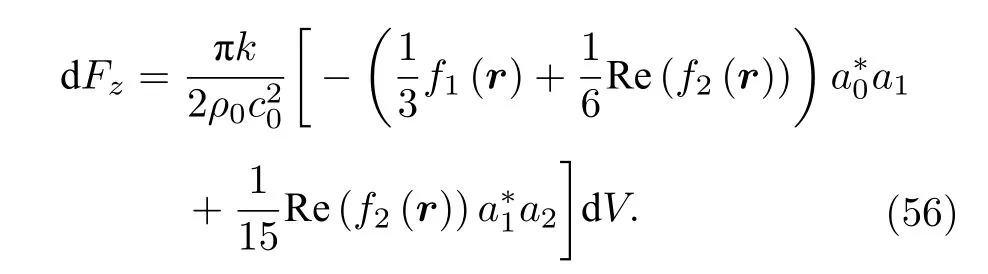
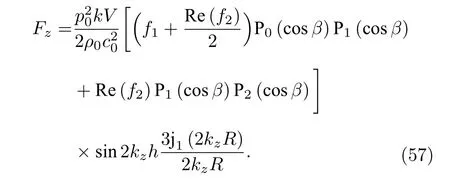
7 结论

