基于局部搜索NSGA-Ⅱ算法的机械产品分组选择装配方法
李 好 徐志玲 徐 勇 赵有为
1.中国计量大学质量与安全工程学院,杭州,3100182.台州方圆质检有限公司,台州,3180003.浙江天马轴承集团有限公司,湖州,313200
0 引言
机械产品的装配由于各零件尺寸链偏差累积,导致合格零件经装配后无法满足企业要求,虽然可通过提高零件制造精度来满足装配要求, 但势必会增加相应的制造成本。选择装配法是在不增加制造成本的条件下,在装配层通过对零件的质量特性进行匹配选择,使产品满足企业的装配要求。
目前,国内外学者主要针对零件的精确选择装配和分组选择装配两种方法进行选择装配方法研究。对于分组选择装配的方法,KANNAN等[1-2]提出了一种基于遗传算法寻求最优分组的方法以获得最小间隙变化,将装配过程分为三阶段,但该方法要求零件尺寸服从正态分布。KUMAR等[3]提出了一种两阶段方法,通过遗传算法来最大程度减少剩余件。RAJ等[4-5]提出了一种基于粒子群算法的选择装配方法,在多质量要求下通过应用分批选择装配法来提高装配效率。RAJESH等[6]提出一种人工免疫系统(AIS)算法,以装配公差变化及质量损失最小为目标,获得最佳装配组合。WANG等[7]提出了一种改进的遗传算法用以解决非正态分布零件的选择装配问题,提高了选择装配的合格率。在精确选择装配方面,任水平等[8]提出构建面向三维空间的同一选择装配信息模型,以公差项为单元的编码方式对多质量要求下的选择装配进行优化。宿彪等[9]针对再制造装配问题,以装配精度和再制造利用率为目标建立选择装配模型,有效提高了重用件和修复件的利用率。王康等[10]提出基于强度Pareto算法对多质量要求选择装配问题进行求解。曹杰等[11]建立考虑形位公差与尺寸公差的选择装配模型,在保证装配精度的情况下,减小产品的形位公差。段黎明等[12]提出考虑零件尺寸与尺寸链关联关系,利用基于密度的多目标进化算法(DMOEA)对多目标选择装配问题进行求解。
综上,精确选择装配能有效提高选择装配中的装配精度以及装配合格率,但大批量生产的方式往往采用分组选择装配。分组选择装配研究通常以零件尺寸服从正态分布为前提,当零件尺寸出现非正态分布时则不适用。本文提出一种非正态分布下的分组选择装配方法,综合考虑装配精度和装配合格率,分析各组成环偏差分布的特点,以决策者对装配精度和装配成功率的偏好选定目标值,借鉴田口质量损失函数构建分组选择装配综合数学模型。利用第二代非支配排序遗传算法(NSGA-Ⅱ)混合模拟退火算法求解数学模型,借助成绩标量函数(achievement scalarizing function,ASF)[13]将多目标问题通过聚合函数转换为一个标量,利用模拟退火算法进行局部搜索,提升种群收敛速度和求解精度,最终得到最优分组方案。
1 非正态分布分组选择装配优化模型
1.1 非正态分布剩余偏差分析
传统的选择装配为获得较高的装配精度,通常在各组成环中挑选合适的零件尺寸相互匹配,使装配而成的产品其封闭环实际尺寸接近理想尺寸,但实际上由于不同的零件加工难度不同,其尺寸分布也不相同,出现非正态分布的情况,如图1所示,如果仍按照传统的方式进行选择装配将产生大量剩余件。徐知行等[14]从所有组成环偏差总体的角度分析,得出封闭环尺寸在平均偏差位置的附近分布概率最大,以封闭环的平均偏差位置为目标值进行选择装配,将获得较高匹配率。封闭环的平均偏差即所有组成环偏差算术平均值的代数和,其表达式如下:
(1)
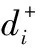
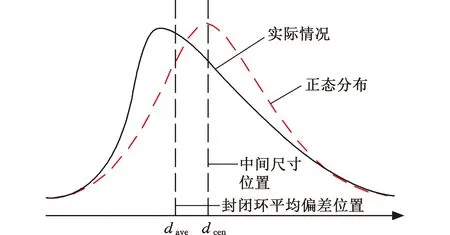
图1 封闭环偏差尺寸分布Fig.1 Closed loop deviation size distribution
通常封闭环的理想尺寸为公差带中心值dcen,若以dcen为目标值进行选择装配,将得到较高的装配精度;若以封闭环平均偏差dave为目标值进行选择装配,则得到较高装配成功率。装配精度和装配成功率无法同时获得最优,两个参数的协调和优选需要决策者根据装配的具体要求,通过加权的方式来选择权重a和b,协调对装配精度和装配成功率之间的偏好,如下所示:
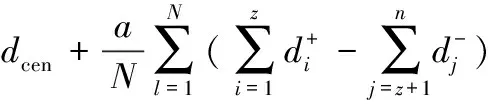
(2)
式中,d0∈[dave,dcen];a,b为[0,1]的常数且a+b=1。
a越大,d0越偏向dave,此时得到较高装配成功率。实际生产中,企业往往优先考虑制造成本,即提高装配合格率,减少生产浪费,其次考虑装配精度。b越大,d0越偏向dcen,使得装配精度越高,产品质量越好。选择偏好a或b由企业的受众群体决定。当封闭环的平均偏差为0时,则dave=dcen,此时的d0即为dcen,即正态分布。
1.2 优化目标函数构建
选择装配既要获得较高的装配精度又要减少剩余件,提高装配成功率,因此是多目标优化问题。以装配精度和装配成功率作为分组配对方案的选择装配质量评价指标,建立模型。
1.2.1基于质量损失函数的装配精度评价指标
由田口质量损失函数定义,质量特征值距离目标值越近,即封闭环实际尺寸与理想尺寸的偏差越小,造成的质量损失越小;反之,造成的质量损失越大。为保证封闭环总的偏差波动最小,提升产品性能,根据田口质量损失函数,构建产品装配质量损失的适应度函数来评价装配质量。由于目标值不一定为公差带的中心值,造成公差带不对称,如图2所示,且在公差带的左端点和右端点造成的质量损失应相等[15],故引入α和β,α、β分别表示公差带左右端点与目标值的距离占总公差带范围的比例,α+β=1,d0-αT、d0+βT分别表示公差带的左边界和右边界,T为封闭环公差带的宽度。
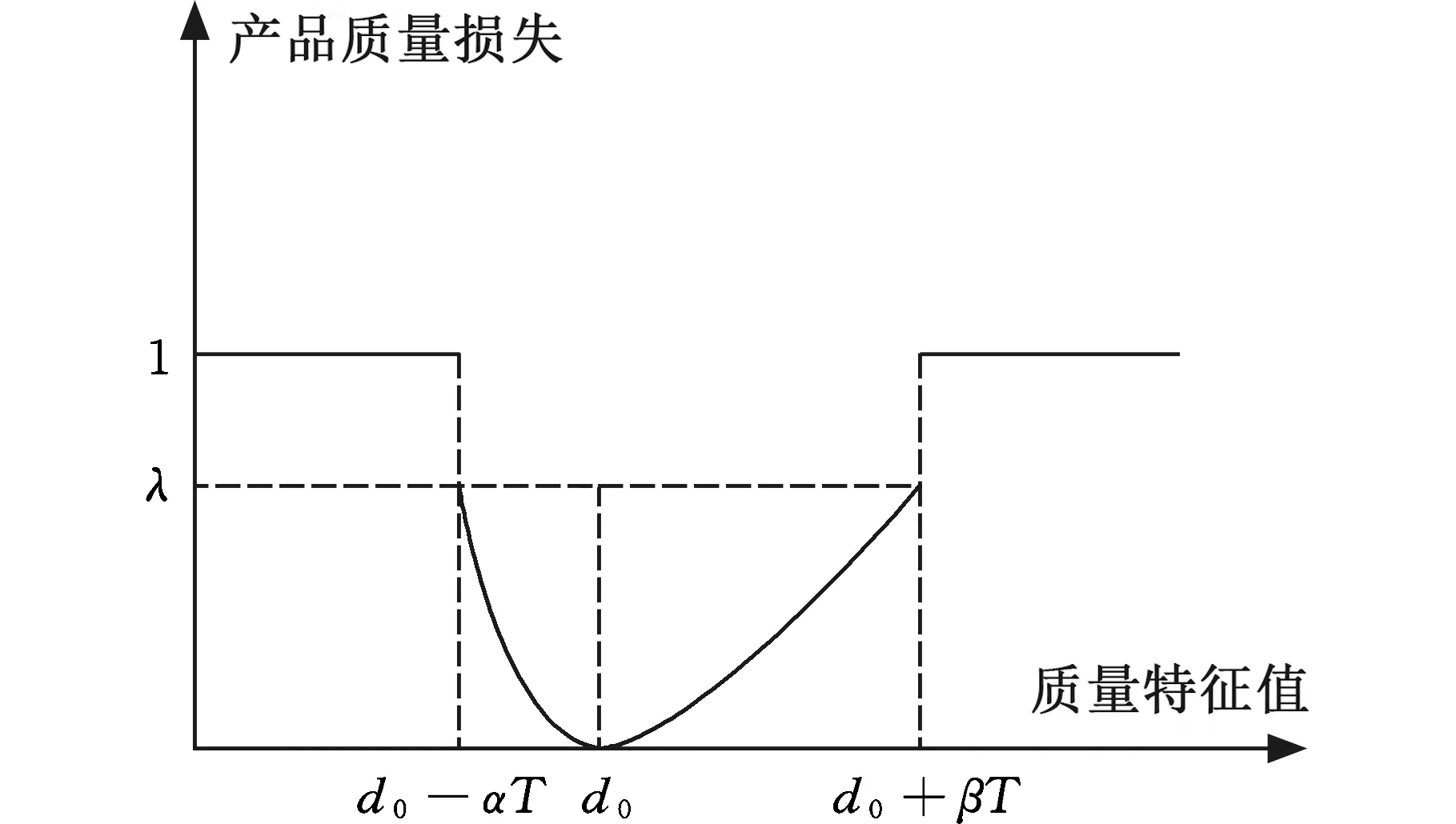
图2 质量损失评价函数Fig.2 Quality loss evaluation function
构建质量损失函数:
q(dp)=
(3)
式中,dp为第p件零件的实际尺寸;λ为[0,1]内的常数,表示产品配合参数位于公差带边界时的可接受程度,根据实际工程经验给出。
在对单个配对关系评价q(dp)的基础上,对整个选择装配方案进行综合评价:
(4)
式中,S为零件分组配对方案。
1.2.2装配成功率评价指标
装配成功率指选择装配得到满足封闭环公差要求的产品数量与参与选择装配总的产品数量的比值,即
(5)
式中,N2为一次选择装配后得到的产品件数;N1为一次选择装配后满足质量要求的产品件数。
1.3 多目标选择装配综合模型
多目标要求下的选择装配,考虑其装配精度及装配成功率对装配质量的影响,定义多目标选择装配综合模型:
minR(S)=[Q(S),δ(S)]S∈Ω
(6)
式中,R为目标函数;Ω表示解空间;δ(S)为不合格率。
为了使目标优化方向一致,令不合格率
δ(S)=1-φ(S)
(7)
2 基于局部搜索NSGA-Ⅱ算法求解模型
NSGA-Ⅱ算法对于多目标优化问题求解具有鲁棒性和收敛性好等特点,通过快速非支配排序比较个体优劣,采用拥挤度比较个体,可保证种群的多样性,但算法局部搜索能力较差,后期的搜索速度较慢。考虑到模拟退火算法局部搜索能力强,在NSGA-Ⅱ算法的基础上以ASF函数作为评价函数,利用模拟退火算法实现局部搜索。
2.1 分组选择装配的编码方法
2.1.1分组数量计算
与传统分组选择装配统一将零件依照过程能力分为6组不同,根据零件的尺寸公差带范围和封闭环公差带宽度,确定零件分组的组数:
(8)
式中,k为分组的组数;Ti为第i个组成环设计公差带的宽度;Tσ为封闭环公差带要求的宽度;ceiling(·)表示向上取整。
2.1.2分组方案编码
为了将分组选择装配方案中的具体信息映射到基因编码中,采用浮点数和整数相结合的编码形式构建染色体,染色体结构如下:
(9)
f=1,2,…,mg=1,2,…,k
式中,m为零件类型的数量;tf,g为浮点数,表示第f类零件的第g组相对公差范围宽度,实际公差范围宽度为tf,g×tf;Gf,g为整数,表示第f类零件中分组的组号为g。
矩阵中的每个元素都由Gf,g+tf,g得到,它的整数部分表示组号,小数部分表示相对公差范围宽度。
对于染色体矩阵,它的每一列所代表的是一个匹配方案,以轴承为例。轴承由外环、内环和滚珠构成,假设它的染色体结构为

(10)
其中,第1列中3个基因的整数部分4、2、1分别表示外环分组中的第4组、内环分组中的第2组和滚珠分组中的第1组进行匹配,组成一个匹配方案;而第1个基因的小数部分0.3149表示外环的第4分组公差带范围占外环设计公差带宽度的31.49%。以此类推,整个染色体结构为总的分组选择装配的方案。
同时,为确保解的可行性,染色体结构应满足:
(11)
即每一行中的各基因小数部分之和为1,且整数部分不重复。
2.2 分组方案的解码方式
为了得到分组选择装配方案中封闭环的实际尺寸,针对分组方案编码,设计了一种解码方法。具体过程如下:
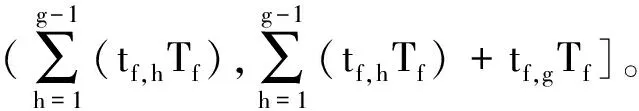
(2)通过遍历操作,将每类零件的尺寸数据存入各分组所对应的空矩阵中。
(3)由于在每个匹配方案中,落在各分组公差带的零件数量会存在不均等或为零的情况,因此Num=min(G1,s,G2,s,…,Gm,s)。其中,s表示任意一列,Num为每一个匹配方案中落在各类零件分组里最少零件的数量,作为这个匹配方案的配对成功数量。假设分组后每组零件的数量分布如表1所示,当一个匹配方案的整数部分为4、2、1时,Num为10,即从A零件的第4组中取10个零件,从B零件的第2组中取10个零件与C零件的第1组中取10个零件进行装配。
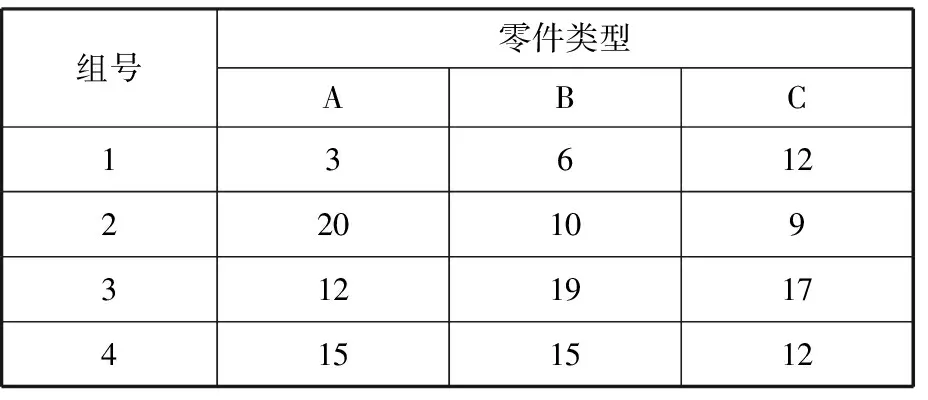
表1 轴承分组后各组零件的数量
(4)为了模拟实际装配过程情形,对于匹配方案的各类零件的选取,均为从各分组中随机选取Num个零件,将它们随机配对,再通过装配尺寸链计算得到封闭环的实际尺寸。
2.3 基于局部搜索的NSGA-Ⅱ算法流程
2.3.1遗传算子设计
2.3.1.1 选择算子
采用锦标赛选择法,每次从种群中抽取一定比例的个体,依据非支配排序层数进行比较;若层数相同,优先选择NSGA-Ⅱ定义的拥挤度高的个体。重复操作,直到新种群规模达到原先种群规模。
2.3.1.2 交叉算子
为充分交换基因位中的基因信息,使交叉前后有较广的空间分布,采用随机两点交叉方法,对参与交叉的两个父代个体中随机选择子串X1、X2进行交叉运算。通过随机的方式确定两个交叉点,再生成一个随机数r,r∈{0,1,2},当r为0时,染色体在交叉点1之后交叉;当r为1时,染色体在两个交叉点之间交叉;当r为2时,染色体在交叉点2之前交叉。图3为随机数为1时的交叉操作。
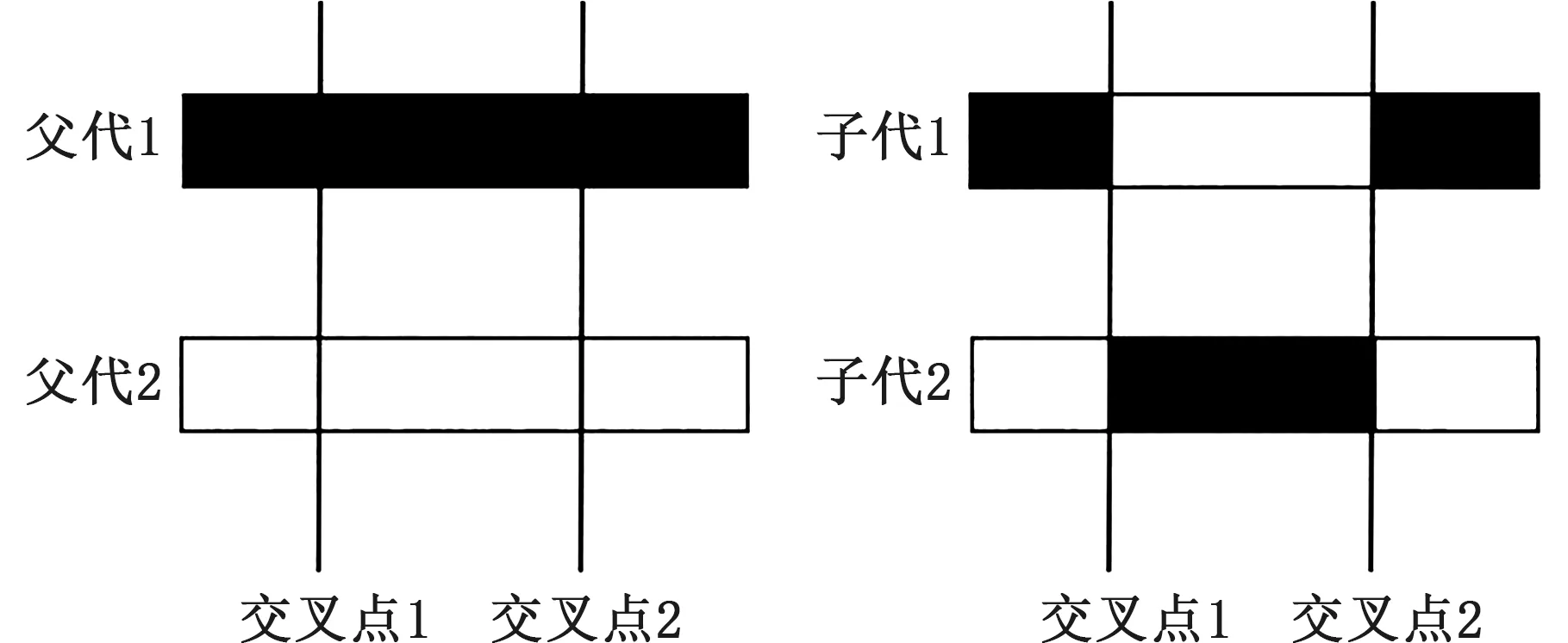
图3 随机数为1时交叉操作Fig.3 Crossover operation when the randomnumber is 1
为了保证染色体在交叉操作中满足式(11)定义的约束保证解的可行性,在交叉操作中将X1的基因保留部分与X2进行比较,从X2中移除与X1基因保留部分相同组号的基因,再对X2余下组号中的分组公差相对宽度进行随机分配,使得X2剩余的基因部分与X1基因保留部分拼接形成新的子代染色体,且新的子代染色体每个基因的小数部分和为1。同理,对X2进行相同的操作生成新的子代。图4所示为一个随机数r为1的交叉操作实例。

图4 随机数为1时交叉操作实例Fig.4 Example of crossover operation when therandom number is as 1
2.3.1.3 变异算子
变异的方法是选择染色体的某个基因作为变异点与该染色体后一位基因位进行交换(若选中了最后一个基因则与第一位基因进行交换),同样为了保证解的可行性,使染色体在变异过程中满足式(11)的要求,交换后的两个基因需要重新分配分组公差相对宽度。
2.3.2基于成绩标量函数的局部搜索
(12)
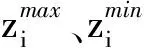
依据模拟退火算法的Metropolis准则,判断是否接受父代中的低劣解作为下一代种群的起始值,接受概率如下:
(13)
式中,P为接受低劣解的突跳概率;Tc为当前温度;B为玻尔兹曼常数;F(Xold)为父代ASF函数值;F(Xnew)为子代ASF函数值。
2.3.3局部搜索的NSGA-Ⅱ算法流程
该算法由输入模块、初始种群模块、评价模块、子代产生模块、局部搜索模块和输出模块构成。算法流程如图5所示,步骤如下:
(1)输入选择装配问题参数:零件的公差带、种类数、零件的数量、装配精度要求;设置算法参数:迭代次数、种群初始大小、交叉、变异概率,初始温度、衰减系数、结束温度。
(2)构建初始种群,通过解码计算出每个染色体代表的装配方案中成功匹配产品的封闭环实际尺寸。
(3)计算适应度值,对父代进行非支配排序和拥挤度计算,再计算父代的ASF值。
(4)对父代种群中的个体进行交叉、变异操作产生子代,计算子代的ASF值。
(5)对子代进行模拟退火搜索,比较父代与子代的ASF值,通过Metropolis准则判断是否纳入新的解集,将新的解集与父代合并。
(6)通过选择操作判断是否满足终止条件或迭代次数大于Z,若满足则输出结果,否则返回步骤(3)。
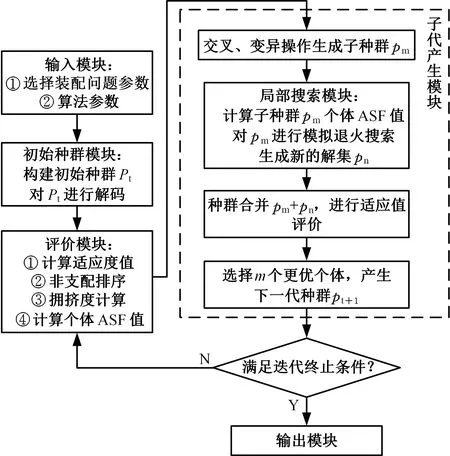
图5 算法流程图Fig.5 Algorithm flow chart
3 实例分析
以某轴承企业生产的6224深沟球轴承(图6)的选择装配为例,设计公差要求见表2。
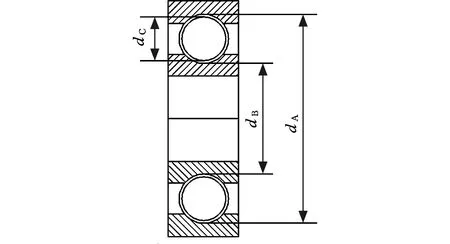
图6 6224深沟球轴承Fig.6 6224 deep groove ball bearing
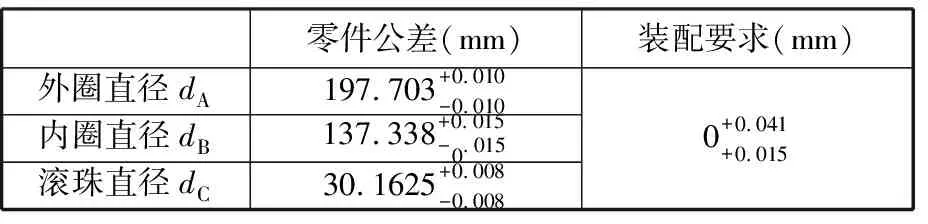
表2 6224深沟球轴承公差设计要求
现场采集的50套轴承产品的待装配零件如表3所示,对其进行选择装配分析。由于滚珠(零件C)的制造精度明显高于内圈滚道(零件B)和外圈滚道(零件A),滚珠尺寸误差可以忽略不计,假设每套轴承产品所用滚珠大小均相等,因此表3给出的零件的尺寸偏差数据中每个滚珠的尺寸偏差代表每套轴承中所有滚珠的尺寸偏差。轴承装配间隙
dp=dA-dB-2dC
(14)

表3 零件尺寸偏差数据
根据式(11)求得分组数k为4,零件的种类m为3,零件数量为50。零件的公差带和装配精度如表2所示,为了优先考虑装配合格率,设定式(2)中a=0.6,λ=0.4,初始种群的大小N为50,交叉概率Pc=0.85,变异概率Pm=0.3,最大进化代数Gen=300,初始温度为100,衰减系数为0.8,结束温度为60。经过多次实验,2个目标函数值最终趋于稳定,有较好的收敛效果,如图7、图8所示,其中最优装配方案如表4所示。
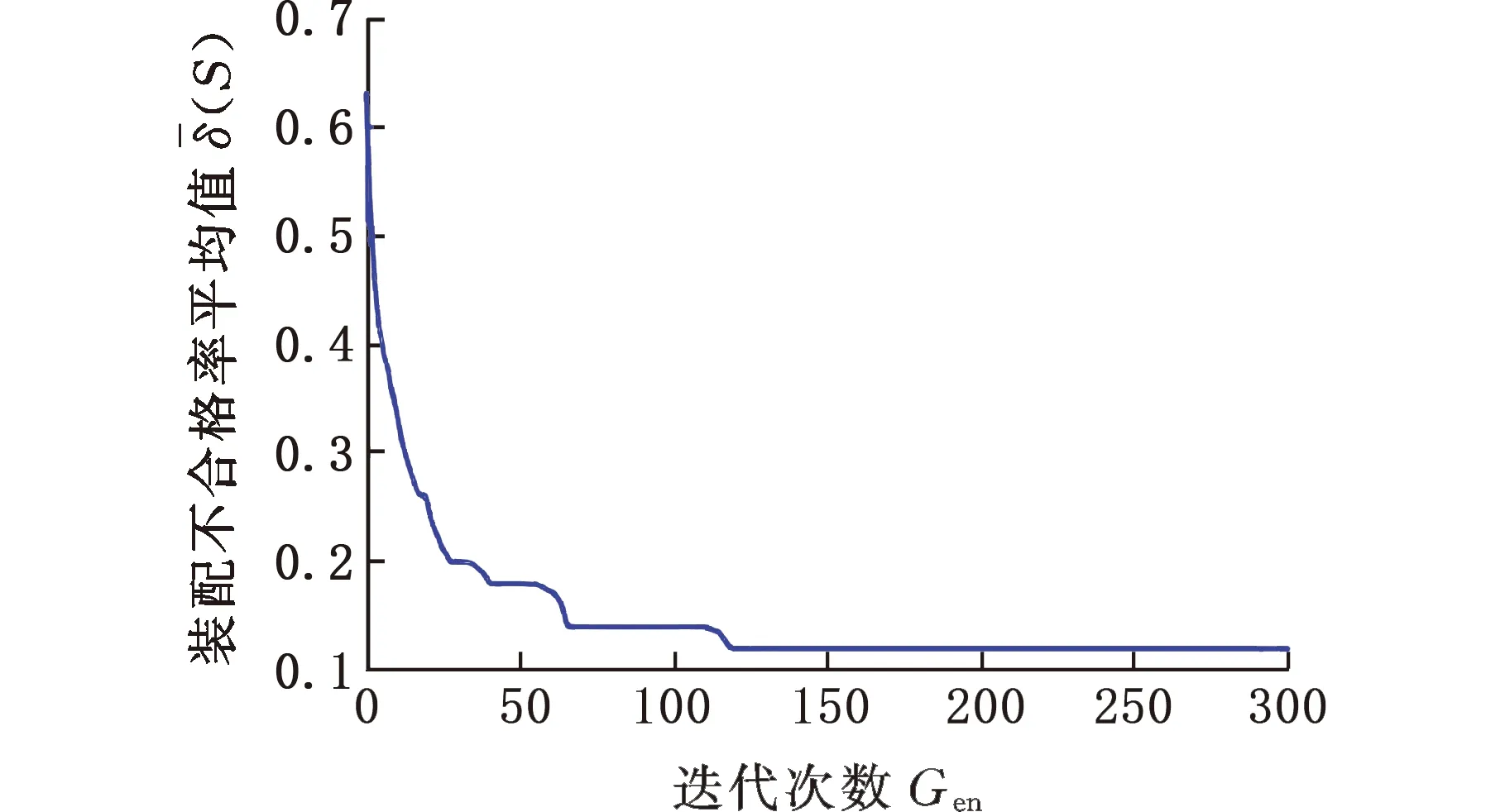
图7 产品装配不合格率δ(S)平均值变化曲线Fig.7 Product assembly failure rate δ(S) averagechange curve
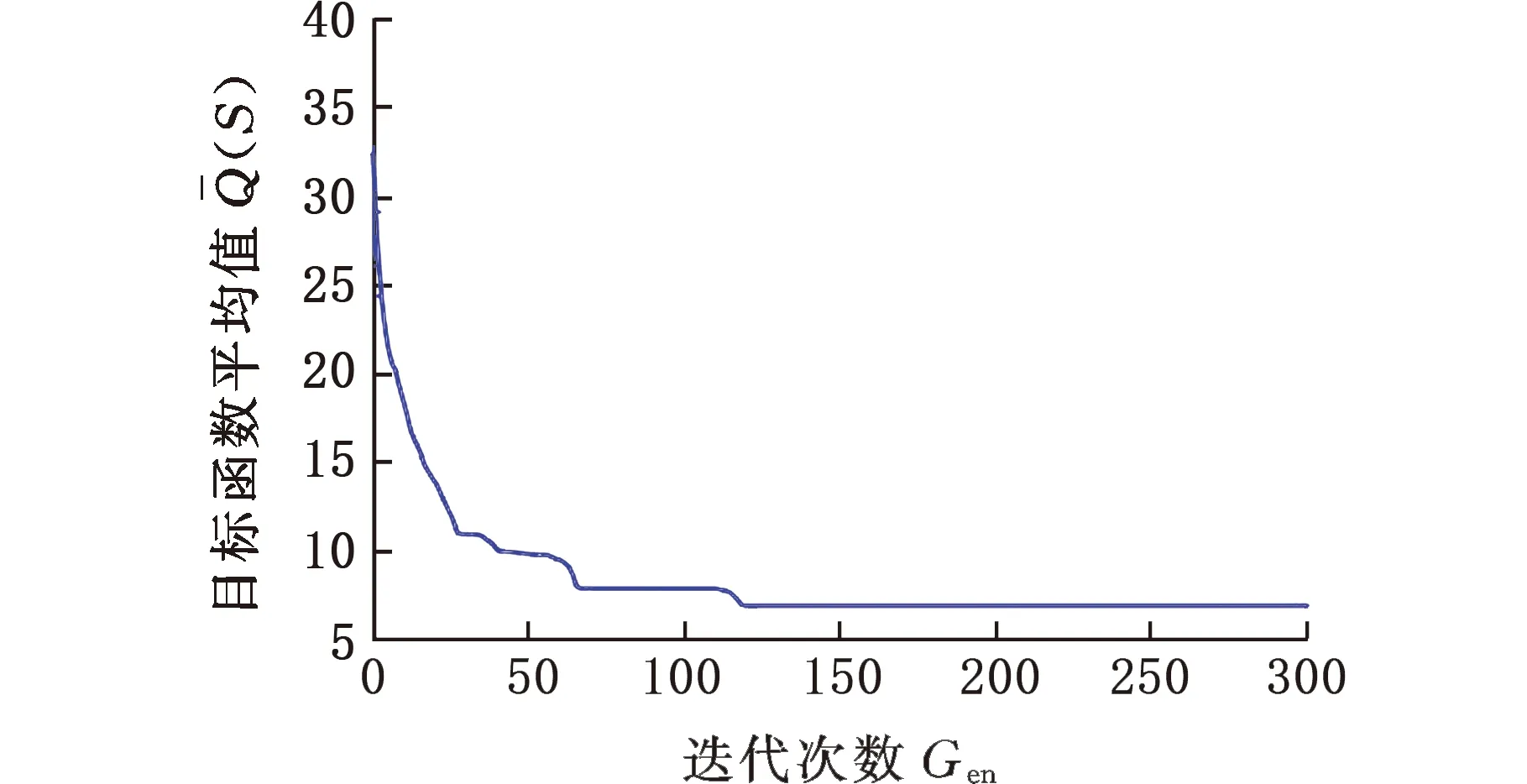
图8 产品装配质量损失Q(S)平均值变化曲线Fig.8 Change curve of Q(S) average value of productassembly quality loss
为了证明方法的有效性,在原始数据相同的情况下,将顺序装配法、文献[8]的选择装配方法与基于局部搜索的NSGA-Ⅱ选择装配方法进行比较,结果如表5所示。可见,由于文献[8]仅考虑产品的合格率,装配精度无法保证,而本文的分组选择装配方法在装配成功率和装配质量方面均优于其他两种方法。
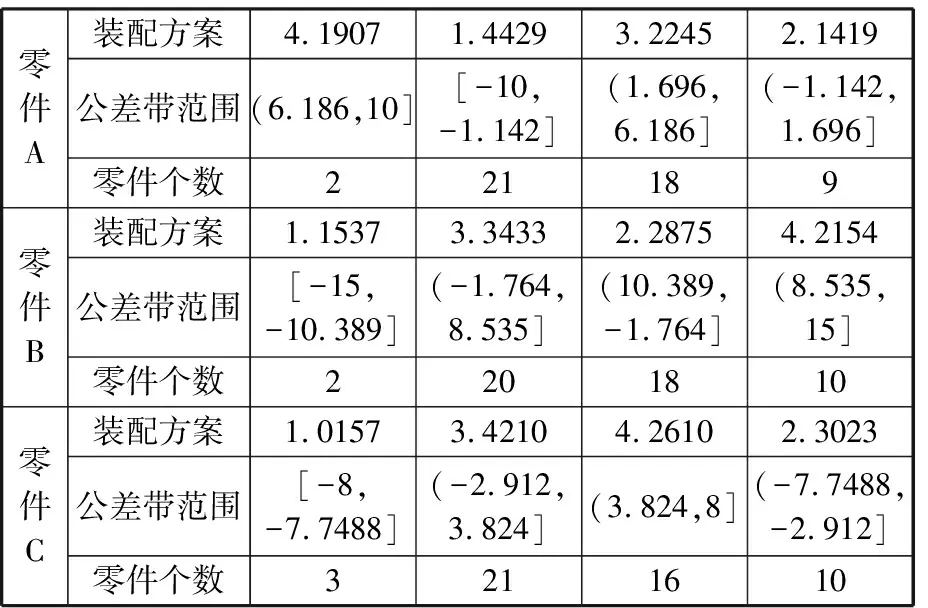
表4 最优分组选择装配方案
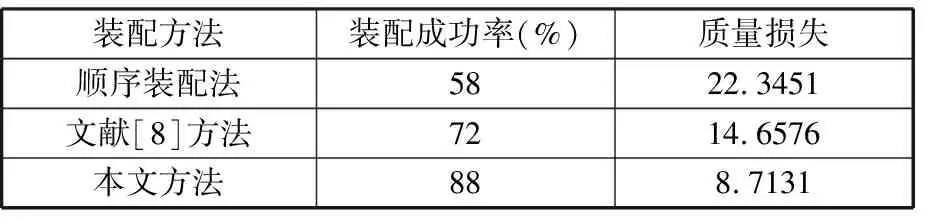
表5 不同选择装配方法的结果
4 结语
本文针对大批量机械产品的分组选择装配问题,当零件尺寸为非正态分布的情况,考虑决策偏好的影响,改进田口质量损失函数,并提出一种分组选择装配的方法,构造了面向分组选择装配的综合数学模型,在保证装配精度的基础上,寻求更高的装配成功率。同时,在NSGA-Ⅱ算法的基础上,利用模拟退火算法进行局部搜索,采用ASF函数将多个目标值转化为一个标量,从而便于应用模拟退火算法。通过实例验证了方法的有效性。此外,本文方法还能有效保证产品的装配质量,得到全局最优的分组选择装配方案。在装配过程中只需从各匹配方案分组中挑选零件,可降低后续装调工作的难度,提高生产效率。

