模指数外包方案ExpSOS 的格基密码分析

郑云海，田呈亮,2+

1.青岛大学 计算机科学技术学院，山东 青岛266071

2.中国科学院 信息工程研究所 信息安全国家重点实验室，北京100093

模指数运算又称模幂运算，其作为一种基本运算广泛应用于RSA 密码体制和DSA（digital signature algorithm）的签名算法中。通常地，指数长比特时大约需要执行1.5次模乘操作，这对于计算资源有限的本地设备来说代价十分昂贵。因此，研究模指数的安全外包具有重要的理论与现实意义。根据方案所基于的安全模型，现有的外包方案可分为两类：基于双服务器的外包方案和基于单服务器的外包方案。

在文献[14]中，Zhou 等提出了一种基于单个服务器的模指数外包方案ExpSOS，旨在安全高效地实现本地端模指数的计算。文中证明了其方案能保护本地端底数、指数和模数的机密性，并能以高概率检测出服务器端的恶意行为。最近，在文献[13]中，Rangasamy 等模仿Chevalier 等的攻击，对ExpSOS进行了简略的安全分析，他们的攻击假设用户调用了两次外包算法且要求两次外包的模指数运算的指数相同，这样的攻击条件是十分严格的。本文对ExpSOS 进行了更全面的评估。具体来说，本文的贡献可以概括如下：

（1）对方案进行了唯密文分析，指出了方案潜在的弱密钥。通过将方案弱密钥的求解转化为模线性多项式的小整数解问题，调用Coppersmith 的格基构造求解算法，仅利用密文就可以在多项式时间内恢复方案中的多个私有参数。

（2）为避免弱密钥攻击，详细估计了安全应用场景下底数和方案中安全参数选取的规模。

（3）实验给出了数字签名标准推荐参数下Exp-SOS 方案的弱密钥攻击实例，验证了理论分析的正确性。

1 预备知识

1.1 常用符号及其含义

一般地，本文用小写加粗字母表示列向量。表1列出了文中常用的专用符号及数学函数。

表1 符号说明Table 1 Symbol description

1.2 格与相关不变量

作为一种经典的数学对象，格在解决计算机科学中的许多计算问题，特别是在密码学领域发挥着重要的作用。

（格）有个线性无关的维向量…b∈R，由{…b}张成的格L定义为：

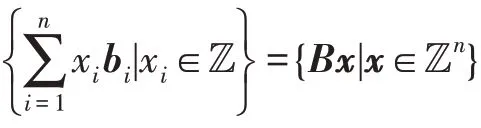
（Minkowski 定理）设L为秩为的格，存在非零向量使得：

1982 年，著名的LLL 算法提出，它可以在多项式时间内找到格L的一个由“短”向量组成的约化基，其具有以下性质：

设L 为秩为的格，在多项式时间内，LLL 算法可以输出一系列约化基向量v,1 ≤≤,满足：

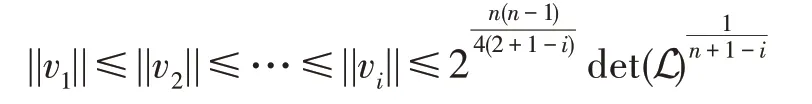
1.3 多项式范数

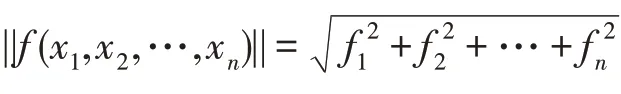
1.4 Howgrave-Graham 定理

（Howgrave-Graham 定理）设(,,…,x)∈Z[,,…,x]为包含个单项式的整系数多项式，若：

2 Zhou 等ExpSOS 方案的回顾

最近，Zhou 等提出了一种底数、指数和模数均可变的外包方案ExpSOS以计算umod。在ExpSOS中，模数的隐私性基于大整数分解的困难问题，底数使用环扩张技术隐藏，指数通过欧拉定理隐藏。即给定3 个大整数、、，它们的两方算法过程如下所示：

3 对方案ExpSOS 的弱密钥分析与改进

本章将给出Zhou 等外包方案ExpSOS 中潜在的安全威胁。确切地说，对此方案在使用不同参数的场景下进行了唯密文攻击，并对安全参数的规模给出了具体的估计。攻击中使用的主要技术是Herrmann和May的格基的求解模线性方程的小整数解的方法。

3.1 Herrmann&May 方法

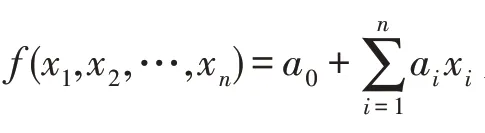
设＞0，是一个足够大的合数且有因数使＞L。设(,,…,x)∈Z[,,…,x]为有个变量的线性多项式。若满足：

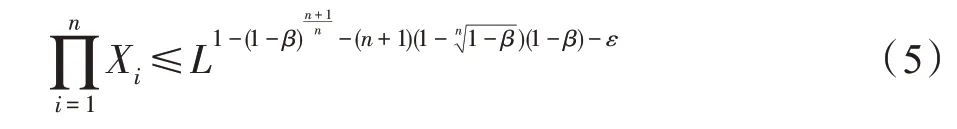
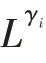
根据Herrmann 和May的分析，可以通过以下步骤将(,,…,x)的小整数解问题转化为寻找格中短向量问题：

（1）通过乘上a-mod将方程(,,…,x)转化为首一多项式(,,…,x)。

（2）构造多项式集合：

（4）通过求解由h(,,…,x)组成的线性系统可以找到(,,…,x)=0 mod的小整数解，其中h(,,…,x)（1 ≤≤）是代数无关的。

3.2 对ExpSOS 的攻击及对策

本节对方案中底数与指数的隐私性进行分析。基于方程（2）～（4），根据定理4，它们的隐私性可以转化为模多项式方程的小整数解问题。通过分析，指出了方案潜在的弱密钥，并给出了方案适用的底数的大小以及方案逻辑拆分中参数的安全取值范围。设ExpSOS 方案中各参数的上界表示如表2 所示。在模指数运算最常见的两个应用场景（RSA与数字签名标准（digital signature standard，DSS））中，模数分别为两个大素数的乘积与一个大素数。本文的分析基于上述两种情景，分别对为大素数和两个大素数乘积两种情况进行分析。

表2 变量上界Table 2 Upper-bounds of variables

3.2.1 为素数时

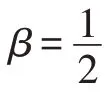
（1）底数的隐私性分析

根据等式（4），有：

3.2.2 为合数时

基于3.2.1 小节与3.2.2 小节安全性分析结果，为避免本文提出的弱密钥攻击，表3 详细总结了不同场景下方案安全参数的选取范围。

表3 安全参数的选取范围Table 3 Selection range of security parameters

4 攻击实例

本章以对方案ExpSOS 的分析为例给出了攻击实例。在本文的例子中使用的所有参数均参考NIST的数字签名标准以及RSA 算法标准。实验使用Wolfram Mathematica 11.3 完成，运行环境为Windows 10，Intel Corei5-6500 3.2 GHz，8 GB RAM。攻击实验结果如表4 和表5 所示。

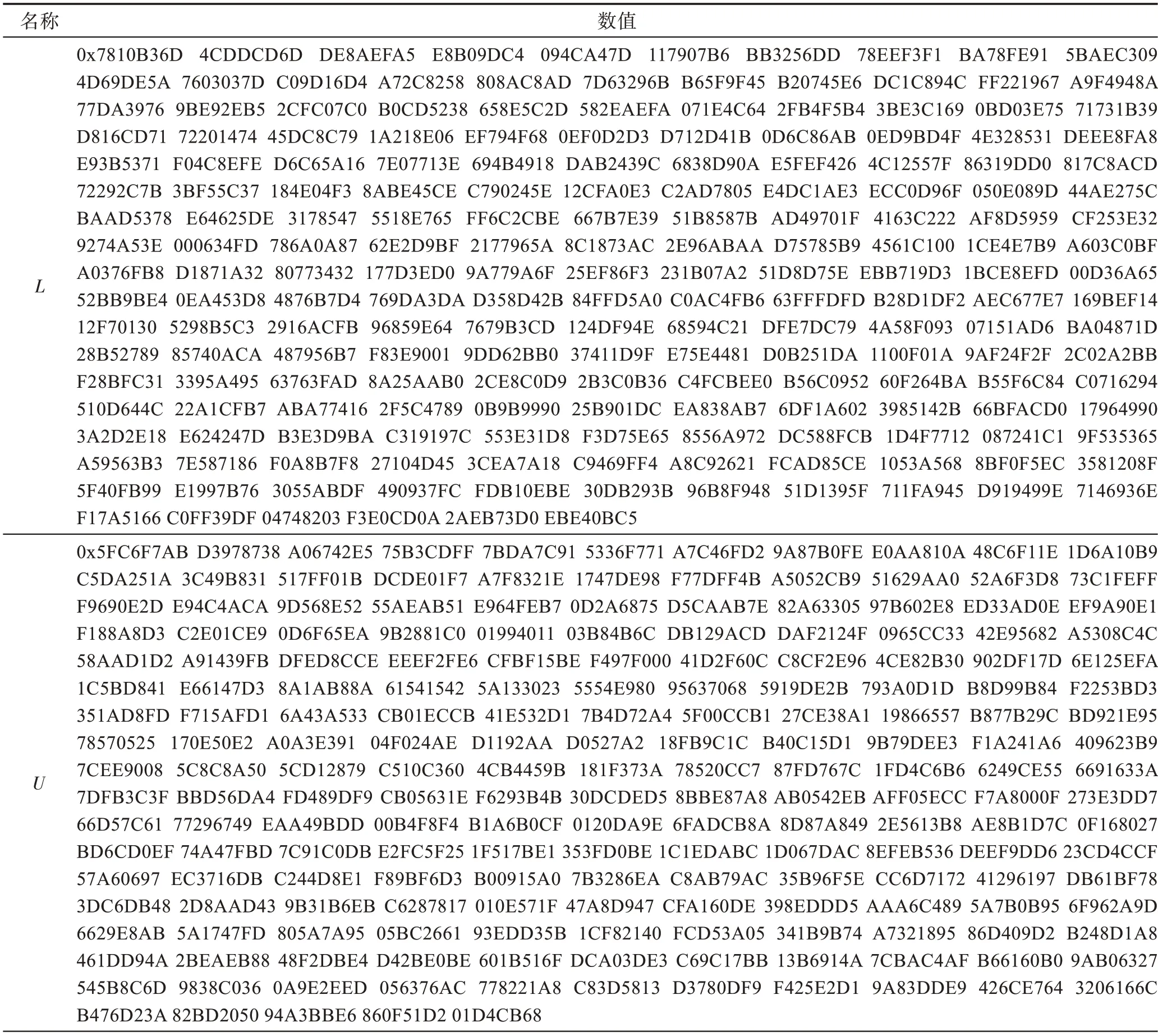
表4 N 为素数时的实验参数及结果Table 4 Experimental parameters and results while N is prime

表4 （续）

表5 N 为合数时的实验参数及结果Table 5 Experimental parameters and results while N is composite

首先描述为素数的攻击实例。取模数为3 072 位的大素数，基数为1 024 位整数，指数为256 位整数。在对ExpSOS 进行仿真之后，表4 列出了云服务器拥有的参数及攻击结果。由于对其他方程的攻击具有极高的时间和空间复杂度，这里只给出基于方程（4）和方程（2）的底数以及指数的恢复攻击实例。根据对等式（4）的分析过程以及实验硬件设备性能，为了平衡空间复杂度和攻击的时间复杂度，取=0.05，计算可得=15，=7，=16，构造对应多项式的系数矩阵，通过攻击可以恢复底数如表4 所示。该攻击实例敌手约化格基的时间成本小于2 min，求解方程组的时间小于0.1 s，总时间合计不超过2 min。

根据对等式（2）的分析以及实验硬件设备性能，为了平衡空间复杂度和攻击的时间复杂度，取=0.2，得=8,=2,=45,构造对应多项式的系数矩阵，通过分析可得如下含有(,)两个未知数的线性多项式，且总能找到所需的根：

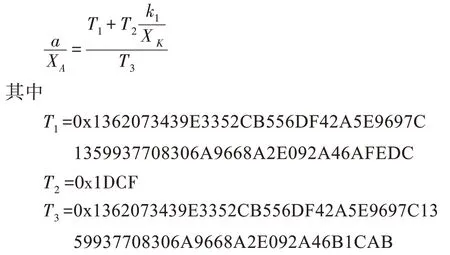
该攻击实例敌手约化格基的时间成本小于2 min，求解方程组的时间小于0.1 s，总时间合计不超过2 min。

下面给出为合数时的一个攻击实例。表5 列出了使用的参数及结果。同样由于复杂度的问题，只给出底数的恢复攻击。分别取两个1 536 位的大素数、′，生成模数=′，选择基数为2 048位。对ExpSOS 进行仿真之后，根据对等式（4）的分析过程以及实验硬件设备性能，为了平衡空间复杂度和攻击的时间复杂度，取=0.05，有=24，=16，=25，构造对应多项式的系数矩阵，通过攻击可以恢复底数如表5 所示。

该实例中敌手约化格基的时间成本小于15 min，求解方程组的时间小于1 s，总时间合计不超过15 min。

5 结论

本文对Zhou 等在IEEE TIFS 2017 提出的模指数外包方案ExpSOS 的安全性进行了全面的分析。通过格基约化技术对其方案进行攻击，并对其中的参数选择提出了建议以抵抗这种攻击。