带有积分边值条件的二阶非线性常微分方程解的存在性

杜睿娟

(甘肃政法大学人工智能学院，甘肃兰州 730070)

0 引言

非线性常微分方程边值问题在工程技术等领域具有广泛的应用背景,如由不同密度的N个部分组成的均匀截面钢丝的振动可以设置为多点边值问题[1]；弹性稳定性理论中的许多问题可以用非线性常微分多点边值问题的方法来解决[2]；小尺寸的桥梁通常设计有两个支撑点,这导致了一个标准的两点边界条件,而大尺寸的桥梁有时设计有多点支撑,这对应于一个多点边界条件[3].基于广泛的工程应用背景,非线性常微分方程多点边值问题解的存在性已经引起了学者的很大兴趣[4-6].1997年，Feng等[6]讨论了二阶常微分方程

x″(t)=f(t,x(t),x′(t))+e(t),t∈[0,1]

在边值条件

和

下解的存在性.

当前，有关解的存在性的结论大多数都是基于m-点边值条件得出的,而对于m-点边值条件的推广,即具有积分边值条件的非线性常微分方程解的存在性的讨论并不多见.此外,已有的讨论共振情形下多点边值问题解的存在性的工作几乎均是基于相关算子的核维数dim KerL=1而获得的，对于核维数dim KerL=2的结论并不多见[6-8].基于以上考虑,文中讨论算子L的核维数dim KerL=2的共振情形下,具有积分边值条件的二阶非线性常微分方程边值问题

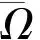
( i )Lu≠λNu, (u,λ)∈D(L)KerL∩∂Ω;

( ii )Nu∉ImL,u∈KerL∩∂Ω;

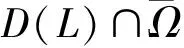
( i )对a.e.t∈[0,1]，f(t,·)在R上连续；

( ii )对u∈R2，f(·,u)在[0,1]上Lebsgue可积；

(iii)对每一个常数ρ>0,存在函数fρ∈L1[0,1],使得

f(t,u)≤fρ(t), a.e.t∈[0,1],||u||<ρ.

注1文中总假设下列条件成立；

1 预备知识

( i )ImL是Z中的闭子集；

( ii )dim KerL=codim ImL<+∞.

文中以X,Z分别表示赋范为

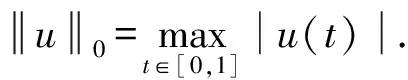
Lu:=u″,u∈D(L)⊂X,

(1)

其中

Nu=f(t,u(t),u′(t))+e(t),t∈[0,1].

引理1算子L如(1)式所定义，假设条件(C1)，(C2)成立，则L为零指标的Fredholm算子.定义线性算子：

则KP为算子L在D(L)∩KerP上的逆算子，即

KP=L-1|D(L)∩KerP,

其中KerP={u∈X：u(0)+u′(0)t=0}，且满足

||KPy||≤||y||1,y∈ImL.

证明证明分五步完成.

(Ⅰ)显然

KerL={u∈D(L):u(t)=a+bt,a,b∈R},

下证

ImL={y∈Z:Q1y=Q2y=0},

(2)

其中

设二阶齐次线性方程

u″(t)=y(t)

(3)

有解u(t)满足边值条件，则

由边值条件和条件(C1)可得Q1y=Q2y=0，即y∈ImL.反之,若y∈ImL，则

Q1y=Q2y=0.

(4)

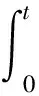
(Ⅱ)证明KerL=ImL.令

易验证T1(T1y)=T1y,T1(T2y)=0,T2(T1y)=0,T2(T2y)=T2y，所以Q2y=Qy,即Qy为线性算子.

若y∈KerL，则Q1y=Q2y=0,于是

从而

因此Q1y=Q2y=0，即y∈ImL.反之,若y∈ImL，则由Q1y=Q2y=0可得y∈KerL，因此KerL=ImL.

(Ⅲ)证明dim ImQ=2，L为零指标的Fredholm算子.设y∈Z,令y=(y-Qy)+Qy,则Qy∈ImQ,y-Qy∈KerQ=ImL,因此Z=ImL+ImQ.令y(t)=at+b,则y∈ImL∩ImQ,由y∈ImL及Qy的定义可知,Q1(at+b)=0,Q2(at+b)=0.由

可得a=b=0，ImL∩ImQ={0}，这表明Z=ImL⊕ImQ.因此codim ImL=dim ImQ=2,这表明L为零指标的Fredholm算子.

为算子L限制在D(L)∩KerP上的逆算子.

(Ⅴ)由KP的定义,有

因此可得||KPy||≤||y||1.】

2 主要结果及证明

定理1假设下列条件成立：

(H1)存在函数m,n,p,q∈L1[0,1]及常数θ∈[0,1]，满足

或者

(H2)令

则存在常数A>0,B>0，当|u(t)|>A，|u′(t)|>B时，有

(H3)存在常数C>0,使得对任意实数a,b，当|a|>C或|b|>C时,有

Q1(a+bt)+Q2(a+bt)>0,

(7)

或者

Q1(a+bt)+Q2(a+bt)<0.

(8)

则当||m||1+||n||1<1/2时，边值问题(1)在C1[0,1]中至少存在一个解.

证明假设条件(5)成立，令Ω1={u∈D(L)KerL:Lu=λNu,λ∈[0,1]}.设u∈Ω1，则λ≠0,QNu=0，即Q1u=Q2u=0.由(H2)可知，存在t1,t2∈[0,1]满足|u(t1)|≤A，|u(t2)|≤B.又因为

所以有

再结合引理1可得

所以

整理得

由常数θ∈[0,1)可知存在常数M>0，使得||u||≤M，因此Ω1有界.

令Ω2={u∈KerL:Nu∈ImL}.设u∈Ω2，则u∈KerL，其中KerL={u∈D(L):u(t)=a+bt,a,b∈R,t∈[0,1]}.由Q(a+bt)=0可知Q1(a+bt)=Q2(a+bt)=0，结合条件(H3)可知，|a|≤C,|b|≤C，从而||u||≤|a|+|b|≤2C，即Ω2有界.

记

若条件(7)成立，令Ω3={u∈KerL:λJu+(1-λ)QNu=0}.设u(t)=a+bt,a,b∈R，u∈Ω3，则λJu+(1-λ)QNu=0.经过简单计算可得

所以

若λ=1，则a=b=0；若λ≠1,则由条件(H3)可知

这与λ(|a|+|b|)≥0矛盾！故Ω3有界.

若(8)式成立，类似可证明Ω3有界.

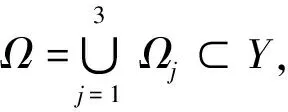
L-紧的，于是定理A的条件( i ),( ii )成立.因为

所以定理A的条件(iii)也成立.