基于MTF-CNN的滚动轴承故障诊断方法

雷春丽，夏奔锋，薛林林，焦孟萱，张护强

(1.兰州理工大学 机电工程学院，兰州 730050；2.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室，兰州 730050)

滚动轴承是现代旋转机械中的重要零部件，其主要功能为支撑旋转部件，减少旋转体之间的摩擦损失。然而，轴承也是最容易损坏的部件，有资料统计，旋转机械失效案例中45%～55%是由滚动轴承失效引起的[1]。滚动轴承的故障可能会导致整个机械系统的损坏，造成大量的经济损失[2-3]。因此，为了保证设备运行时的安全性和可靠性，对滚动轴承进行故障诊断和在线监测是很有必要的[4]。传统的机械系统健康监测方法需要手动提取故障特征，在面对故障信息丰富多变、实际工况交替复杂时往往会导致诊断效果不理想和泛化性能欠佳的问题[5]。因此，研究既能避免人工提取特征方法的不足又具有强大适应能力的智能故障诊断方法具有重要意义。

传统智能故障诊断方法通过对原始振动信号的时频域分析来完成对信号特征的提取和故障识别。不少学者做出了大量的研究。乔志城等[6]采用改进经验小波变换获取信号的模态分量并完成重要分量的重构，再通过最小熵解卷积对重构信号进行滤波，最后完成轴承的故障诊断。何勇等[7]通过遗传算法优化变分模态分解，之后通过模态分量的包络谱判断轴承故障类型。Saidi等[8]利用经验模态分解将信号分解为本征模态函数(intrinsic mode function,IMF)，再对IMF信号进行双谱分析，最后提取轴承故障特征频率实现故障诊断。这些方法虽然能有效诊断轴承故障，但需根据经验人工提取故障特征，往往存在鲁棒性差、泛化性能不强、技术人员难以胜任故障诊断任务等问题。

传统智能故障诊断方法适应能力较弱，在复杂多变的工况下表现较差，且过分依赖于诊断专家的经验，因此，需要研究出一种适应能力强、受人工提取特征影响较小的故障诊断方法来解决传统方法的不足。Hinton等[9]正式提出了深度学习的概念，克服了人工提取特征的困难，在计算机视觉、语音识别、自然语言处理、图像识别等领域已取得了丰硕的成果[10-13]。随着深度学习的发展，越来越多的学者将其引用到故障诊断领域中。李巍华等[14]将深度信念网络直接应用于轴承振动原始信号的处理，实现轴承故障的分类识别。Verma等[15]利用堆叠式稀疏自编码器提取稀疏特征，对轴承以及阀门进行故障诊断。

卷积神经网络(convolutional neural network，CNN)是深度学习的代表算法之一，因其具有强大的自动特征提取功能而被广泛应用于图像识别。近年来，CNN被故障诊断领域的部分学者应用于故障分类任务中。2016年，Janssens等[16]首次利用CNN对齿轮箱中的轴承、齿轮等进行故障诊断，将常规算法故障诊断率提高了6%。宫文峰等[17]通过试验全面地分析了CNN中比较有效的深度学习技巧、模型超参数对滚动轴承故障诊断结果的影响，但并未考虑负载改变时的诊断效果。Udmale等[18]将包含时频能量的谱峭度图输入到CNN中进行故障诊断，提高了轴承在变工况下的识别精度，但并未考虑数据集规模大小对模型的影响。Liang等[19]提出了一种并行卷积神经网络，融合了时域特征和频域特征，在不同负载和少量故障数据时均获得了较高的识别准确率，但该模型结构复杂，不利于故障的快速诊断。Wen等[20]将原始振动信号转化为二维灰度图像，输入CNN中进行故障诊断取得了较好的诊断效果，但该方法并未考虑信号的时间相关性且存在故障信号信息丢失的问题。

本文利用马尔科夫转移场(Markov transition field，MTF)考虑信号时间相关性的优点，提出一种新的MTF-CNN滚动轴承故障诊断模型。首先采用MTF对原始一维振动信号进行编码，转化为具有时间相关性的二维特征图像，然后将特征图作为CNN的输入进行自动特征提取和故障诊断，最后实现对不同故障类型的分类。本文选用凯斯西储大学轴承数据库的数据验证所提方法的有效性。并在负载改变时和不同数据集规模条件下对所提方法的泛化性能进行了深入分析，同时与支持向量机(support vector machine,SVM)、BP神经网络(back propagation neural network,BPNN)和基于时域分析的CNN等常用智能算法进行对比分析。结果表明，相较于其他常用的智能故障诊断方法，本文所提方法在滚动轴承故障诊断中具有更好的识别精度和泛化性能。

1 马尔科夫转移场

马尔科夫转移场可将原始一维振动信号转化为新的时间序列二维图像[21]，该方法主要是通过马尔科夫转移概率来实现动态转移信息的编码。

给定一个时间序列X={x1,x2,xi,…xn}，首先将X离散化为Q个分位数单元，用分位数qj(j∈[1,Q])量化时间序列的每一个值，通过识别分位数，将每个数值xi映射到相应的分位数qi上，并构造一个Q×Q的邻近加权矩阵W(马尔科夫转移矩阵)，通过沿时间轴以一阶马尔可夫链的方式将分位数转换成矩阵W，其表达式如式(1)所示

(1)

式中,wij为分位数qi位于点分位数qj后的概率,即wij=P(xt∈qi|xt-1∈qj)。

由于马尔科夫转移矩阵忽略了时间序列X的分布与时间步长ti之间的时间依赖关系，故构造马尔科夫转移场来弥补这一不足，MTF通过沿时间顺序排列每个概率来扩展矩阵W，即为矩阵M，表达式如式(2)所示，矩阵M包含了每个分位数与时间步长之间的时间相关性。

(2)

式中,mij为分位数qi转移到分位数qj的转移概率，即mij=P(qi→qj)。

MTF通过上述编码方式将时间序列可视化，转换为具有时间相关性的二维特征图像，如图1所示，MTF图像编码方式主要由以下几个优点：①通过考虑每个分位数与时间步长之间的依赖关系，保留了原始信号在不同时间间隔内的时间相关性；②由于一维信号与MTF二维图像编码方式为映射关系，避免的一维信号信息的丢失；③用不同深浅的颜色体现出分位数之间的转移概率大小，有利于充分利用CNN在图像分类中的优势。

图1 时域波形图和MTF特征图像

2 卷积神经网络

卷积神经网络(CNN)是一类包含卷积计算且具有深度结构的前馈神经网络，传统CNN模型通常由卷积层、池化层、全连接层和Softmax分类器组成，其原理是通过多个能提取输入数据特征的滤波器对输入的图像进行卷积和池化运算，逐层提取出具有显著特征的特征图，将获得的特征图通过全连接层，再对模型进行误差计算和参数优化，最后通过分类器输出相应的结果。

2.1 卷积层

卷积层也叫做特征提取层，是CNN的核心组成部分。卷积层通过不同尺寸的卷积核与上一层输入图像进行卷积运算，得到相应的激活图像，通过激活函数提取图像特征。卷积运算的公式如式(3)所示

(3)

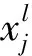
2.2 池化层

池化层又称为下采样层，一般与卷积层相连接，其作用是对特征进行下采样操作，降低计算量，防止过拟合。池化层的下采样操作可表示为

yn=down(x,g)[n]=g(x(n-1)m+1:nm)

(4)

式中：m为池化宽度；x和y分别为输入和输出；down(·)为下采样函数；down(x,g)[n]为down(x,g)的第n个元素；本文采用最大池化，故g(x)=max(x)。

2.3 全连接层

全连接层使用ReLU函数作为激活函数，通常与最后一个池化层相连，起到收集特征和分类的作用，全连接层进行的操作为

δi=f(aiσi+bi)

(5)

式中：i=1,2,…,k；δi为第i个输出；ai和bi分别为第i个神经元的权值和阈值；σi为前一层的输出；f为激活函数。

2.4 Softmax分类器

Softmax分类器位于全连接层之后，以Softmax函数作为激活函数，完成对目标的分类。Softmax函数的数学表达式为

(6)

式中：i=1,2,…,k；δi为上一层第i个节点输出;K为输出节点的个数;即分类的类别个数；pi为每一个输出的概率，所有pi之和为1。

2.5 损失函数与训练优化算法

损失函数通过对预测样本和真实样本标签产生的误差进行反向传播从而优化网络参数。在CNN多分类问题中，常用交叉熵函数作为Softmax分类函数的损失函数来衡量模型输出结果与真实结果之间的差异性，交叉熵值越小，模型预测效果越好。其公式如式(7)所示

(7)

式中：p(xi)为样本的真实概率分布;q(xi)为模型预测的概率分布。

在反向传播的过程中，使用Adam自适应优化器对网络参数进行优化，利用梯度的一阶矩估计和二阶矩估计动态调整每一个参数的学习率从而更新权值与偏差，计算求得参数的最优解[22]。

LeNet-5是一个经典的CNN网络模型，在解决图像分类的问题中得到了广泛应用。本文选取该模型完成滚动轴承故障的分类，LeNet-5网络基本结构如图2所示。

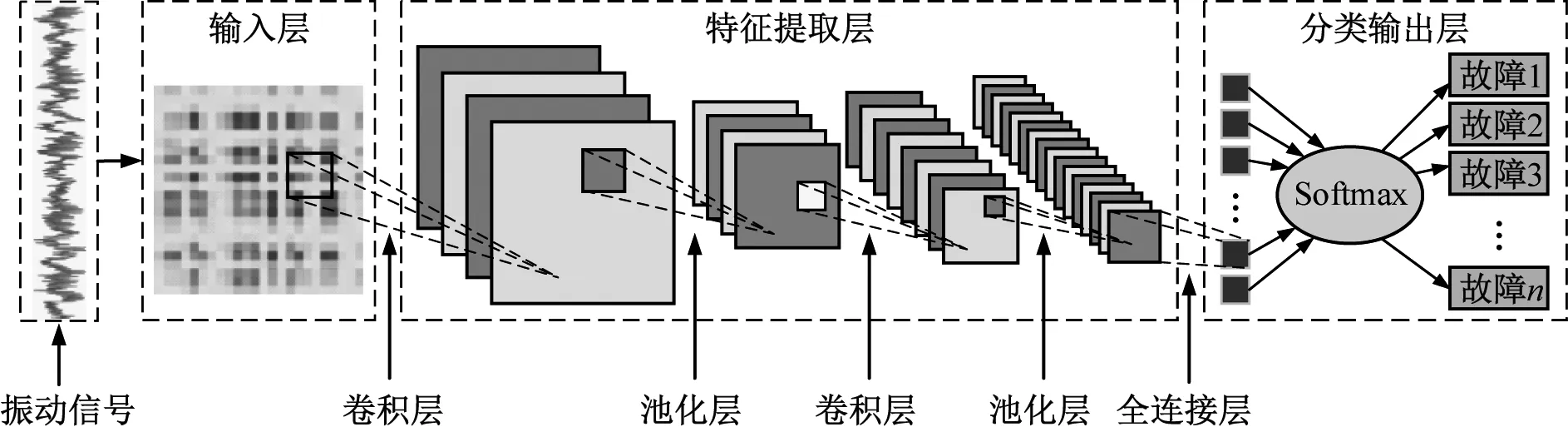
图2 LeNet-5卷积神经网络基本结构图

3 基于MTF-CNN滚动轴承故障诊断方法

本文所提方法充分结合了MTF编码方式可以保留信号时间相关性和CNN强大的自动特征提取功能的优点，提出了基于MTF-CNN滚动轴承故障诊断方法，基本流程如图3所示。在模型的训练阶段，通过Softmax分类函数进行反向传播，使用Adam优化器动态调整网络权值与偏差，最终使损失函数达到最小值，完成模型参数的训练；在模型测试阶段，采用已训练好的CNN模型对新的故障数据进行特征提取计算，最后输入Softmax分类器完成故障分类并输出测试准确率。

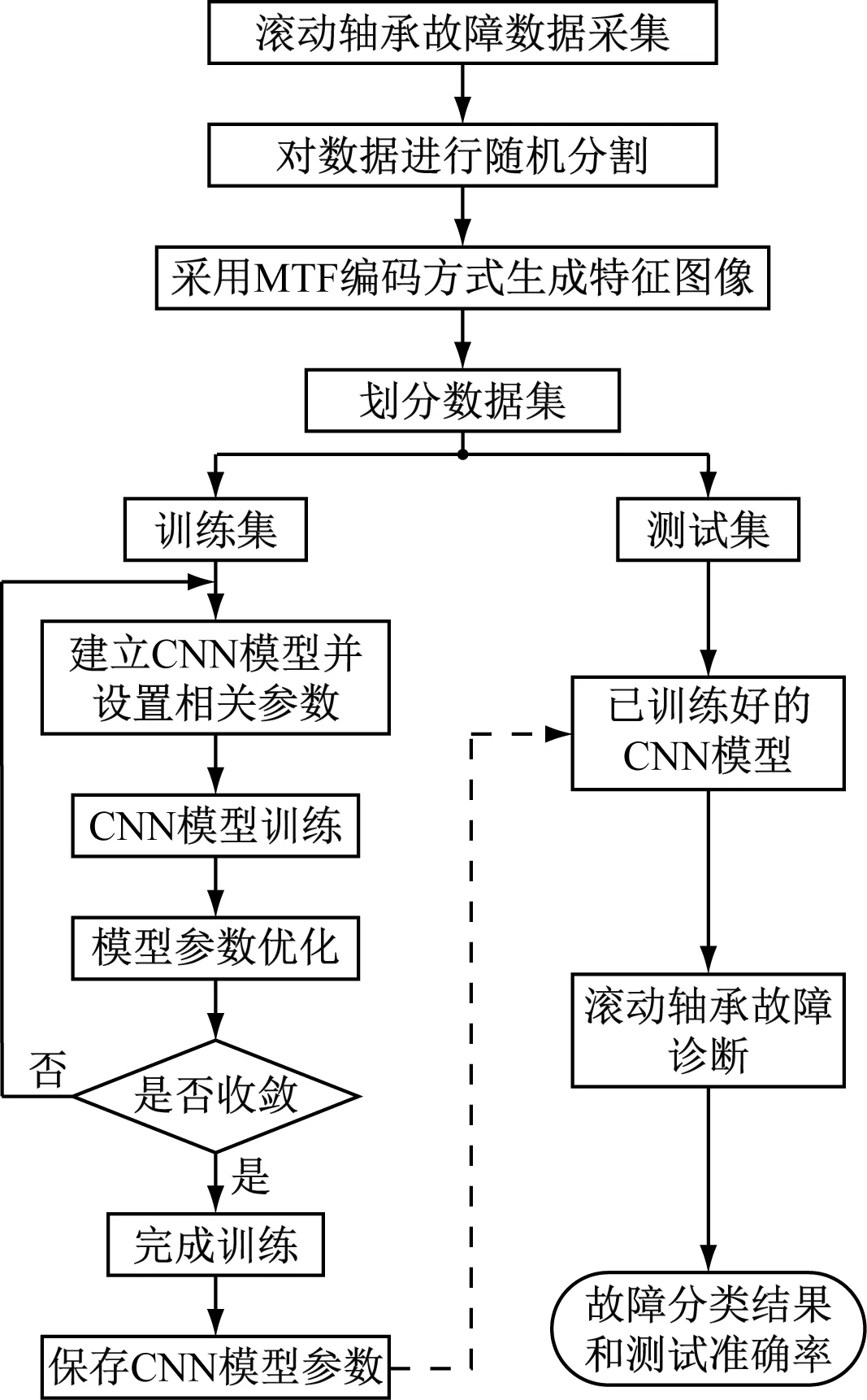
图3 基于MTF-CNN的滚动轴承故障诊断方法流程图

该方法具体步骤如下：

步骤1获取滚动轴承原始振动信号，用于CNN模型的训练。

步骤2对采集到的信号按设置的样本长度进行随机分割。

步骤3将分割后的每段信号按MTF编码方式转换为二维特征图像。

步骤4将二维特征图像数据集按比例划分为训练集和测试集。

步骤5搭建CNN网络模型，初始化参数。

步骤6把训练集输入CNN模型进行预训练，利用优化算法反复对模型参数进行优化，若达到最优值则进行步骤7，否则跳转到步骤5，修改模型参数，直到获得最优参数为止，并保存最佳模型。

步骤7将测试集数据输入到训练好的CNN模型中进行滚动轴承故障诊断，最终获得轴承故障分类结果及测试准确率。

4 滚动轴承故障诊断试验验证与分析

4.1 试验数据集

本文所用滚动轴承故障数据集来自美国凯斯西储大学(Case Western Reserve University，CWRU)轴承试验数据中心在互联网上公布的试验数据[23]。该试验台构成如图4所示，主要由三相异步电机、扭矩传感器和负载组装而成，并将加速度传感器安装在电机磁性底座外壳上用于采集故障轴承的振动信号。本文选取试验台驱动端轴承在载荷为1～3 hp(1 hp=0.745 7 kW)3种工况下工作时采集的故障振动信号，信号采样频率为12 kHz，采样时间为10 s。轴承故障形式为点蚀，轴承的内圈、外圈和滚动体表面故障均由电火花技术加工而成，选取数据库中具有代表性的两种轴承故障类型，故障直径为0.18 mm和0.36 mm，另外包括正常轴承共计7种故障类型。

在本试验中，轴承最低转速为1 772 r/min，通过公式N=fs×60/ns计算出一个周期内的采样点数为406个，为充分保证每个数据样本故障信息的完整性和可信度，本文设置每个数据样本长度为2 048个采样点，并采用重叠采样的方式对数据进行随机分割。将7种原始一维振动信号进行样本数据标签化，每类信号包含400个样本，共计2 800个样本，并按照3∶1的比例划分为训练集和测试集，具体轴承故障样本分布如表1所示。

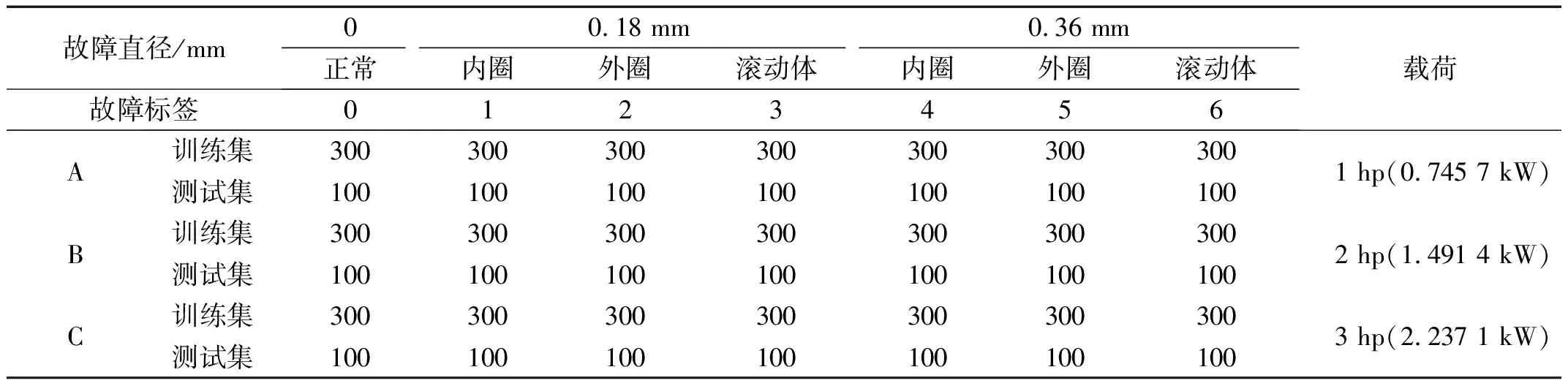
表1 滚动轴承故障样本分布

4.2 特征图像的生成

4.2.1 数据增强

卷积神经网络作为深度学习的代表算法之一，往往需要大量的数据样本才能保证计算的准确性，在现有数据量有限的情况下，采用数据增强的方法满足训练所需样本的数量，在增加样本多样性的同时，提高模型的鲁棒性，防止发生过拟合。本文采用重叠采样的方式对原始一维振动信号进行数据增强，示意图如图5所示，其中实线框内整个信号表示原始信号，每个虚线框内的信号即为样本信号。

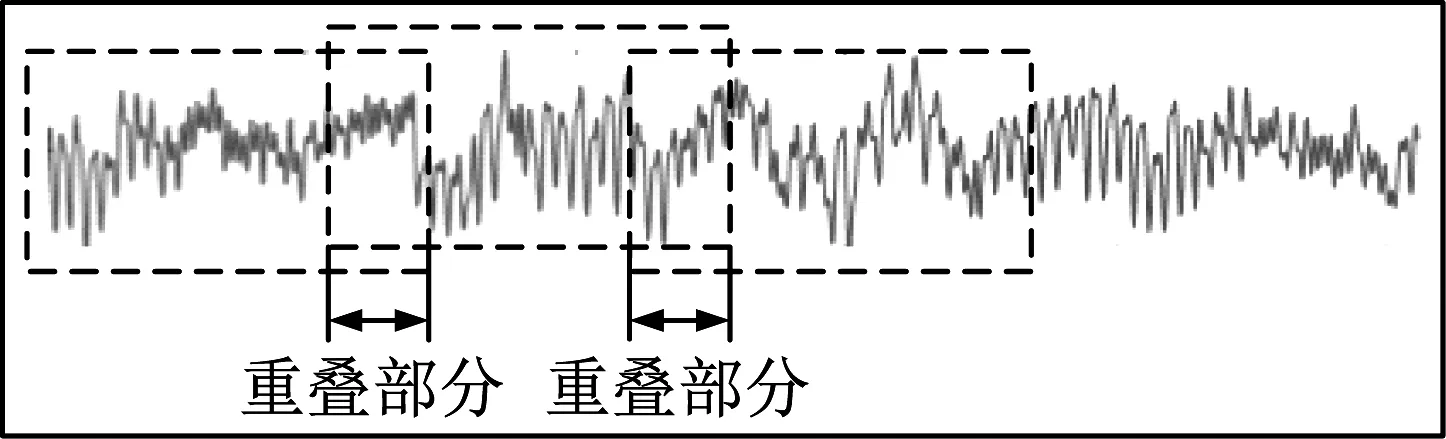
图5 重叠采样数据增强示意图

4.2.2 MTF特征图像的生成

传统的时域分析难以清晰地识别出滚动轴承的损伤程度，无法保证对故障类型的精确分类，因此，利用MTF编码方式考虑信号时间相关性的优点，将信号按设置的数据样本长度随机分割为不同的小段并生成MTF特征图像，如图6所示。

图6 7种轴承故障的MTF编码特征图

4.3 试验结果分析

根据关键参数对模型识别率的影响分析，选取Batch Size=10，Kernel Size=5，并设置迭代轮次为30，卷积层采用ReLU激活函数，参数优化器选取Adam自适应优化器，设置学习率为0.001，Dropout的值为0.5，即每次训练随机选取一半神经元失活，其余一半用来正常训练，以防止网络结构过拟合。

选取负载为1 hp即数据集A进行测试，模型经过30轮训练得到图7结果。分析图7可知，模型在训练集上准确率达到99.86%，在测试集上达到99.71%，经过15轮训练后，训练损失率降到0.006 8并趋于平稳。验证了MTF-CNN模型在滚动轴承故障诊断中具有较好的诊断效果。

(a)准确率

为了进一步考察MTF-CNN模型对滚动轴承故障识别的能力，引入混淆矩阵对诊断结果进行量化分析。混淆矩阵详细地反映了滚动轴承不同故障类型下的误判数量和误判类型，如图8所示。图8中:横坐标代表不同故障的预测类别;纵坐标代表不同故障的真实标签;矩阵主对角线上的数字代表对每类故障正确分类的样本数量。

由图8明显可知：700个测试集样本只有2个样本被错分，均为故障尺寸为0.36 mm的外圈故障被误判为故障尺寸为0.18 mm的滚动体故障。说明了MTF-CNN模型在滚动轴承故障诊断中具有优异的故障识别能力。

图8 故障诊断分类结果混淆矩阵

4.4 模型在不同负载情况下的泛化性能分析

在实际工况中，滚动轴承的负载往往会发生改变，因此，在不同负载情况下故障诊断模型依然能具有良好的诊断效果是非常重要的。为了验证本文所提出模型在不同负载时的优越性，选用3种不同负载下故障数据分别构建训练集和测试集，例如图9中的B→C表示以数据集B作为训练集、数据集C为测试集，测试结果均取5次计算的平均值。

本文与SVM、BPNN和基于时域分析的CNN 3种常用的智能故障诊断方法进行对比分析，最终结果如图9所示。从图9可以看出，各个算法在负载相同时的诊断结果均比不同负载时要好，本文提出方法的识别准确率均比其他方法要高，以负载为3 hp(2.237 1 kW)即表中C→C为例，本文方法的识别准确率为99.83%，比其他算法中效果最好的CNN高0.59%，比SVM高5.23%，比效果最差的BPNN高16.52%。在负载改变时，本文方法诊断性能的优越性更加凸显。由图9可知，本文方法在不同负载时的平均识别准确率均高于其他方法。CNN的诊断效果相较于其他常用算法更好，在前4种负载改变的工况下，均能保持97%以上的识别准确率，在A→B时最高，达到98.21%，但是依然低于本文方法的99.68%，同样在这4种情况下，本文方法的识别率均在98%以上，在B→A时更是达到99.74%，而在C→A和C→B情况下，CNN识别率降低到了86%以下，分别为85.26%和85.74%，本文方法则保持稳定，达到了98.6%和99.69%，均远高于CNN；BPNN在不同负载时效果最差，识别准确率均不如其他3种算法；SVM只有在A→C时的识别准确率高于80%，其余情况均属于70%～80%，均低于本文方法。此外，从图9的误差线可以看出，本文方法的误差均低于其他3种方法，主要原因是当负载改变时，3种常用算法的诊断结果的不确定性增加，误差也随之增加。经过上述对比分析证明了本文所提MTF和CNN相结合的方法在不同负载情况下的滚动轴承故障诊断中具有更好的泛化性能。

图9 各算法在不同负载时的识别准确率

4.5 模型在不同数据集规模下的性能分析

在实际工况中，故障数据量通常是有限的，当采用小数据集时，由于深度学习网络参数过多，模型可能会出现过拟合，导致模型无法获得较高的识别准确率，因此，在数据集较小时保持良好的诊断效果变得非常重要。在数据集A中，分别考虑不同算法在总数据集的100%、60%、30%和10% 4种不同规模数据下进行对比分析，用4种方法对缩减后的故障数据集进行了5次测试，结果如表2所示。

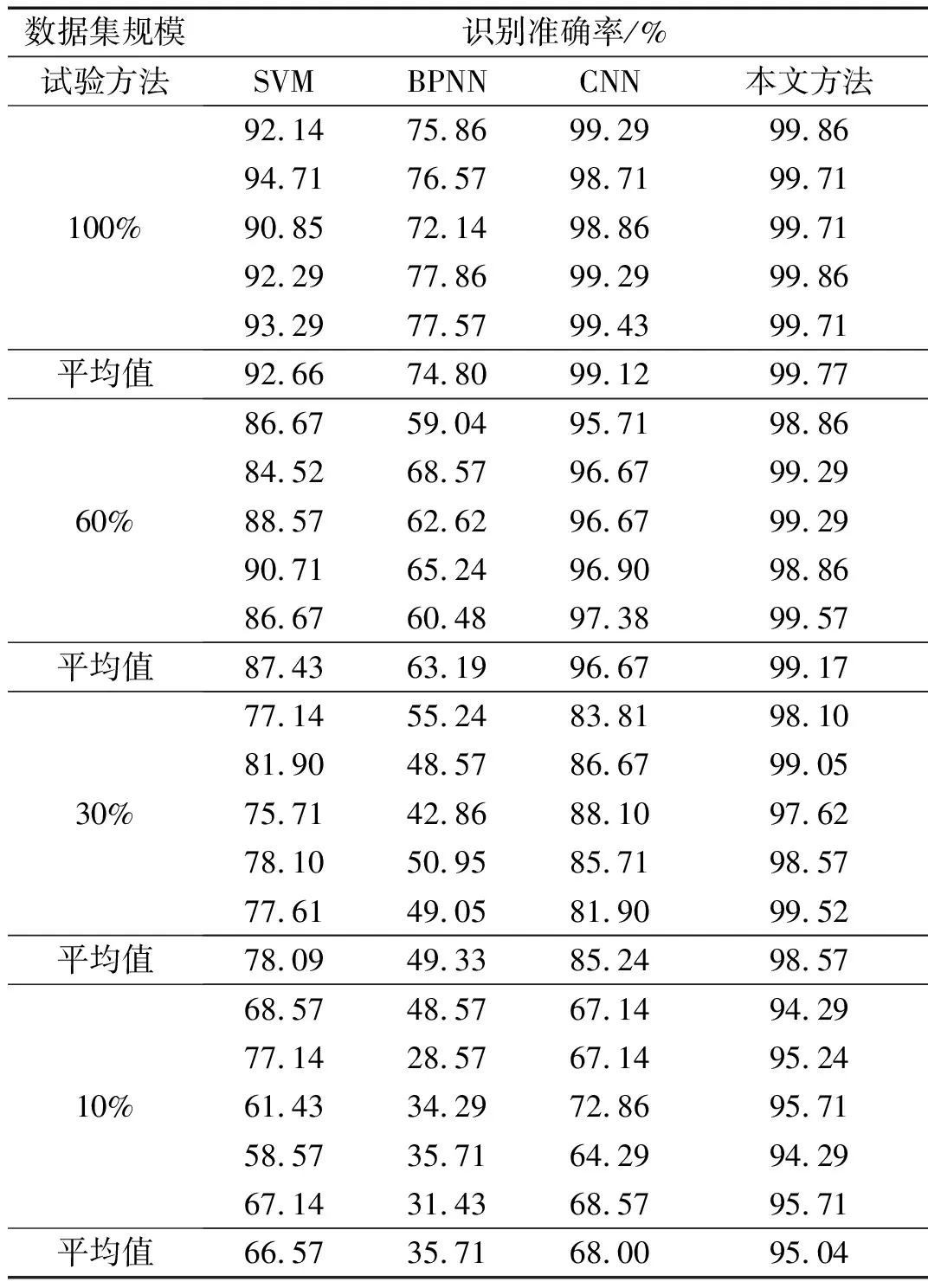
表2 不同数据集规模下的模型识别准确率

本文所提方法在4种不同规模数据下的平均识别准确率均高于其他方法，在数据规模为总数据集时，本文方法为准确率为99.77%，高于SVM的92.66%、BPNN的74.80%、CNN的99.12%；随着数据规模的减小，其他3种方法的识别精度均明显降低，BPNN在数据集大小为总数据集的10%时，准确率下降到了35.71%，是所有方法中最差的，比基于总数据集时降低了39.09%，SVM和CNN分别也降低了26.09%和31.12%。相比之下，在数据集规模减小时，本文方法在数据集大小为总数据集的10%时识别率依然能达到95.04%，只比100%时低4.73%。这些结果表明当数据集规模减小时，本文所提方法均比其他方法具有更高的识别准确率。

不同规模数据集的诊断性能也可通过箱型图来说明，以比较不同网络识别结果的稳定性，如图10所示。从图10可以看出，所提出的MTF-CNN模型在所有情况下都具有较好诊断效果，并且方差较小。除了在100%和60%数据集下CNN的结果表现出较小方差，其他算法在所有情况下方差都较大，并伴有异常值的出现。结果表明，与几种常用的故障诊断方法相比，所提方法能显著提高滚动轴承故障识别效果的准确性和稳定性。

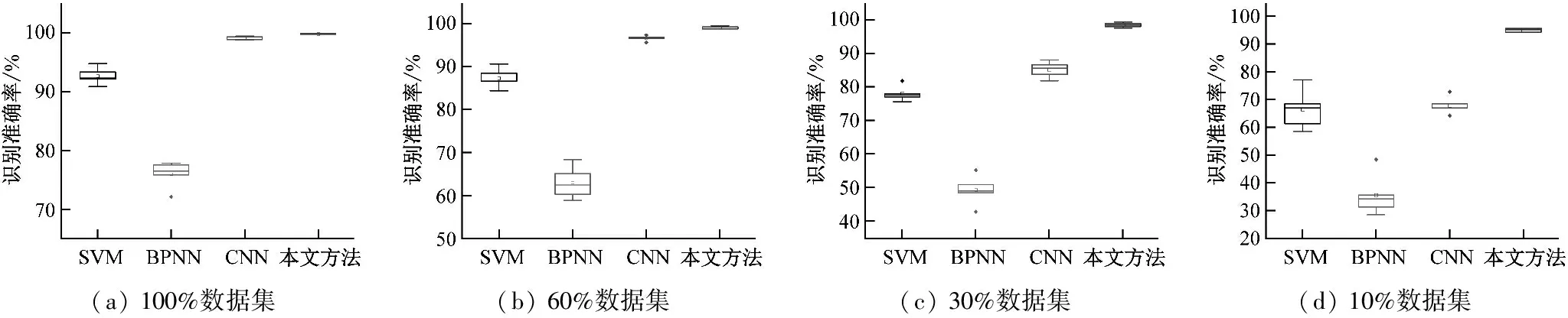
图10 各算法在不同数据集规模下的识别准确率箱型图

5 结 论

本文针对实际工况中滚动轴承受负载复杂多变、数据集较小的影响，使得轴承故障诊断难以获得较高识别准确率的问题，提出了一种基于MTF-CNN的滚动轴承故障诊断方法。采用MTF对原始振动信号进行编码，将所得二维图像输入CNN中实现故障诊断，具体工作内容和相关结论如下：

(1)MTF在对原始信号进行编码时保留了信号的时间相关性；该编码方式的映射关系解决了信号故障信息容易丢失的问题。结合LeNet-5卷积神经网络模型对滚动轴承故障进行故障诊断，最终获得了99.71%的识别准确率。

(2)研究所提模型在不同负载工况下的泛化性能，选用不同负载的训练集和测试集进行试验验证，并与其他常用智能算法的进行对比分析。结果表明，相较于其他算法，MTF-CNN模型在负载改变时仍然保持了较高的诊断精度，具有更好的泛化性能。

(3)研究所提方法在不同数据集规模下的诊断效果。结果表明，MTF-CNN模型在数据集规模减小时依然获得了较高的识别准确率，在数据集大小为总数据集10%时的平均准确率达到了95.04%，比其他算法具有更好的稳定性。

(4)本文虽然研究了实际工况中载荷变化多、故障信号数据集小对滚动轴承的影响，但仅是对于单一故障而言，而实际中多个轴承故障并存工况更为复杂，因此，在未来将对轴承复合故障进行深入研究。