基于群锚承载力的巷道锚杆支护设计及应用研究

牛宏新

(新疆水利水电勘测设计研究院，新疆 乌鲁木齐 830000)

1 矩形巷道塑性区范围

通常采用等效圆法和压力拱法对矩形巷道塑性区的分布范围进行计算。其中，等效圆法是根据圆形巷道计算塑性区范围的方法来确定矩形巷道塑性区范围；压力拱法则是运用普氏压力拱理论确定矩形巷道围岩塑性区范围的计算方法[1-2].

经开挖后，在围压作用下巷道顶板和两帮产生变形，巷道壁面岩体受到拉应力的作用，围压达到巷道极限承载力时会发生破坏，使得围岩相互支撑作用之间发生剪切破坏，巷道顶部和两帮岩体发生垮塌[3].当围岩破坏到一定程度又会重新建立新的应力平衡状态，使围岩岩体不再垮塌，此平衡结构体类似于一个拱形结构。矩形巷道破坏范围见图1.在地下岩体工程中，当巷道埋深过浅时无法形成具有承载能力的有效压力拱结构，通常要求巷道埋深H大于2～2.5倍的顶板压力拱高度[4].

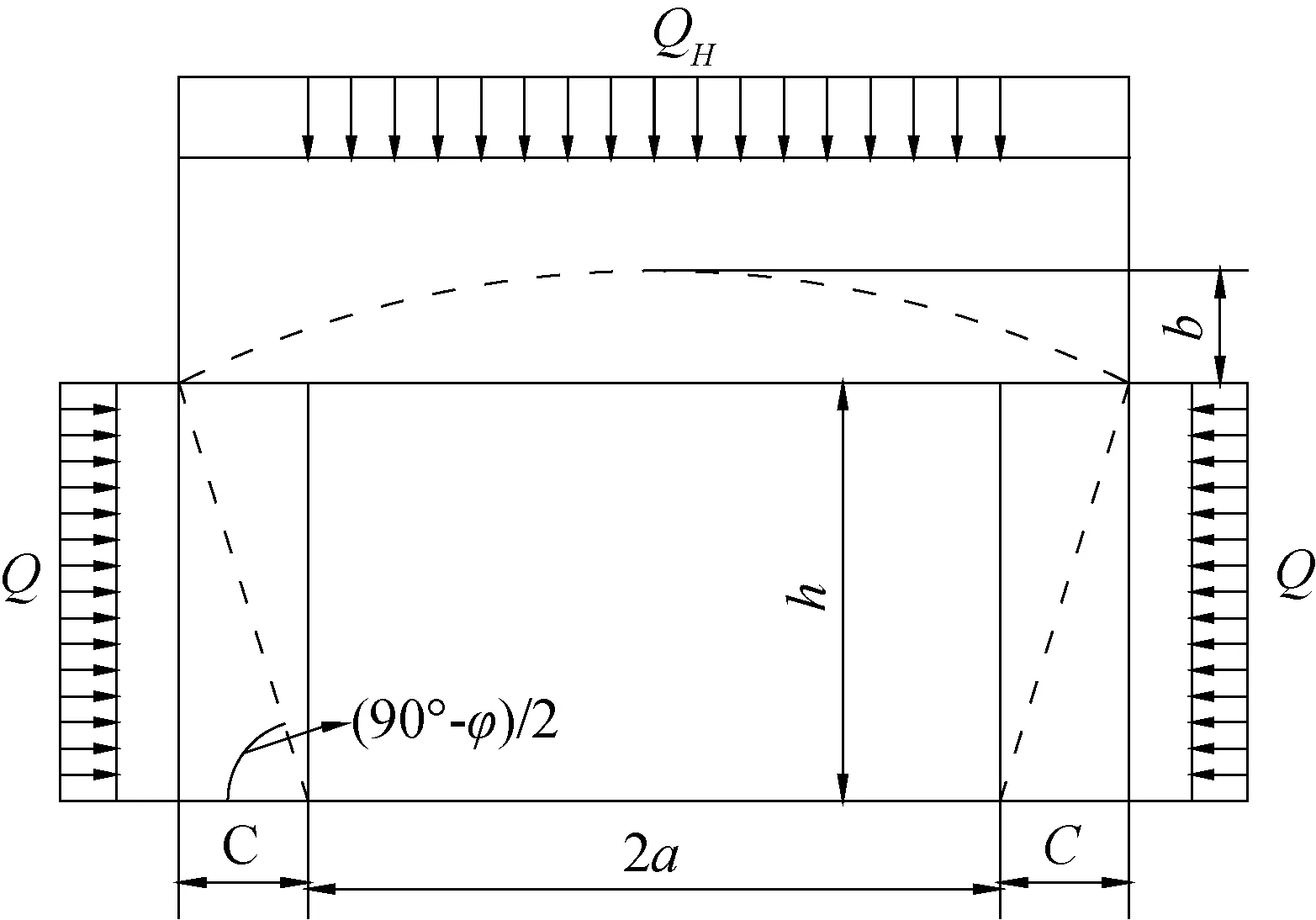
图1 矩形巷道塑性区范围图

依据普氏拱理论能够计算出矩形巷道压力拱高度b以及两帮松动范围C：

(1)

(2)

式中，h为巷道高度；b为巷道顶板冒落高度；f为围岩普氏系数；a为巷道半跨；φ为围岩内摩擦角。

2 矩形巷道围岩塑性剪切破坏

矩形巷道开挖后，其顶板应力一般受切向压应力控制，在巷道两肩与两帮的拐角处成为应力集中最为严重的区域[5].切向压应力的存在极易造成倾斜顶板岩层出现裂缝，从而产生沿裂缝表面滑动的剪切力；当顶板岩层发生破坏后，顶板位移增大使其产生离层，岩石块之间的挤压和错位在其自身重量的作用下导致失稳和损失。在巷道两帮的支撑压力和水平地应力的作用下，两帮表面的岩体在与两帮成一定角度下被剪切破裂，沿节理面发生剪切破坏，造成围岩的垮塌及巷道失稳破坏等[6].

巷道失稳是指锚杆破坏，单个锚杆的破坏形式通常由加强体和锚固剂形成的圆锥破坏体从岩体中被拉出[7]；很多学者做了群锚效应相关的研究，至今还没有将岩体与锚杆看成一个整体来计算锚杆承载力的。论文基于塑性极限平衡理论，将破坏体看作圆锥体，对单锚极限承载力的计算公式进行了推导[8].在单锚极限承载力基础上，对有关群锚极限承载力的计算公式进行进一步的研究[9].

2.1 岩体的应力状态

Mohr认为岩体的破坏形式为剪切破坏且破坏面上的剪应力τf为此破坏面上法向应力σ的函数，该函数为摩尔包线，即：

τf=f(σ)

(3)

当岩体任意一点的剪应力达到了岩体的抗剪强度，该点便达到其极限平衡状态，岩体便开始发生剪切破坏。假设在任意单元体上的大主应力为σ1，小主应力为σ3，大主应力与其作用平面成任意角α的平面上的正应力和剪应力分别为τ、σ，在剪应力与正应力的坐标系中直径为(σ1-σ3)的摩尔圆上的一点如图2所示，即：

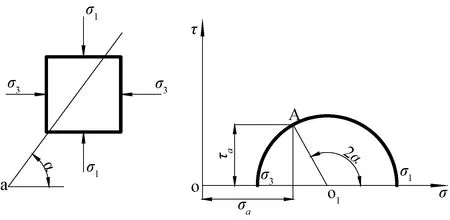
图2 岩体中任一点的应力示意图

(4)

(5)

2.2 岩体的极限平衡条件

可以根据抗剪强度包线与极限应力圆之间的几何关系建立起岩体的极限平衡条件，见图3.

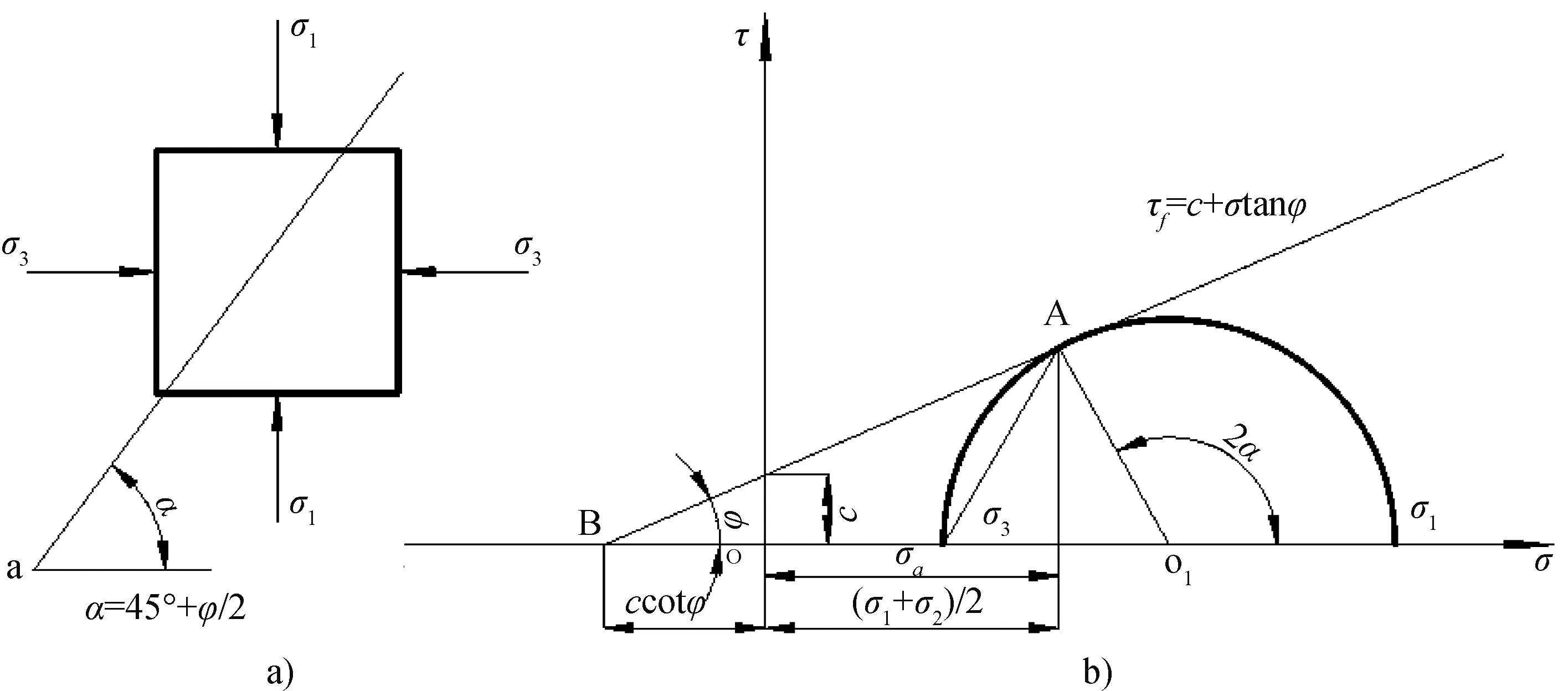
图3 岩体在平衡状态时的摩尔圆与破坏示意图

(6)

由摩尔圆半径可知：

(7)

(8)

由此可得：

(9)

由三角函数之间的换算可得到岩体的极限平衡条件为：

(10)

(11)

根据直角三角形ΔO1AB角度之间的关系可知：

α=45°+φ/2

(12)

可得破裂面与最大主应力面成α=45°+φ/2的夹角。

3 单锚极限承载力确定

锚杆在预应力及围岩压力作用下，锚固体受压形成一个坚实的岩体，同时锚杆拉力在围压的影响下向岩体四周扩散；对于锚固段的单元体在应力极限状态时，锚固段的锚固力产生的压应力比围岩的压应力大,会发生剪切破坏，锚杆轴线与剪切破坏面形成夹角为(45°-φ/2)的圆锥体破坏体，φ为铅锤面与破裂面之间的夹角。

本文基于塑性极限平衡理论，同时假设破坏岩体为圆锥体状的岩土块体，对单锚极限承载力的计算公式进行推导。根据此计算方法，对群锚杆极限承载力的计算公式进行进一步推导，该计算方法思路明确，假设更符合实际工程，利于岩土工程设计的应用。就此方法作如下假设：

1)岩体为理想的刚性介质，且满足Mohr-Colomb破坏准则的条件。

2)破坏岩体以锚杆为轴线，岩体剪切面作为母线，两者所形成的夹角为(45°-φ/2)的圆锥体，速度间断面见图4.

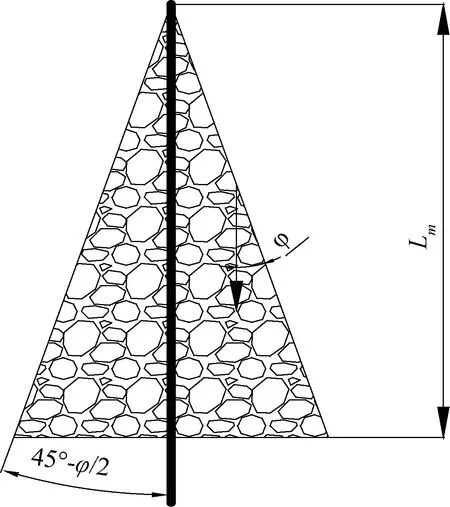
图4 单根锚杆锚固段破坏示意图

3)在剪切破坏范围内，破坏块体为三维轴对称块体。

3.1 顶板单根锚杆极限承载力

根据图4对单根锚杆的极限承载力进行求解。根据岩石的塑性极限理论可知，当岩体发生很小的滑移时，设滑移岩块应变速率为V，滑动面的强度服从M-C强度理论，岩体的重度为γ，黏结力为c，内摩擦角为φ，锚杆与垂直面的夹角为α，F为单根锚杆的承载力，则外力(锚杆拉力和重力)所作的功为：

(13)

内力消散功为：

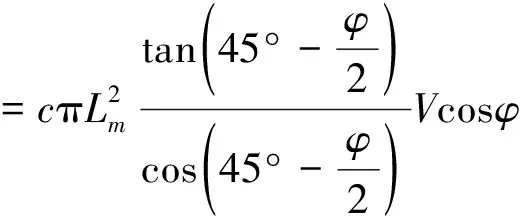
(14)

式中，Lp为锚杆自由段长度；Lm为锚杆锚固长度。

由W外=W内得顶部单根锚杆承载力为：

(15)

3.2 帮部单锚极限承载力

由顶部锚杆受力可知，帮部锚杆的外力仅有锚杆拉力：

(16)

内力消散功为：

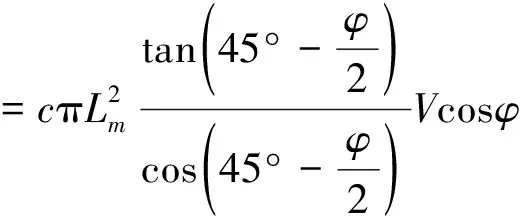
(17)

由W外=W内得帮部单锚承载力为：

(18)

4 群锚承载力确定

根据单根锚杆的破坏形式可得，单根锚杆作用的最大影响范围为圆锥体的直径R=2Ltan(45°-φ/2)；当群锚杆中的锚杆轴间距均大于单锚最大影响范围时，锚杆应力区彼此之间互不影响，群锚的极限总承载力不受影响，等于各单根锚杆极限承载力之和，即F群=nF(n为群锚杆的根数)。

如果锚杆横向和竖向之间的距离比圆锥体的直径小时，则岩体中会产生应力叠加效应，造成总承载能力的降低，同时会产生群锚效应。围岩破坏体不是圆锥体而是群锚共同作用形成四棱台体。其破坏断面图见图5.

图5 群锚杆巷道顶板岩体破坏示意图

4.1 顶板群锚极限承载力

延用单锚极限承载力计算理论可推导出群锚极限承载力计算公式。设群锚沿垂直与巷道方向的尺寸为SX，平行与巷道方向的尺寸为SY,则拉拔力和破坏块体所受重力所做的外力功为：

(19)

其中：

(20)

由于锚杆间距过大，锚固段在剪切破坏时内部损耗功为：

(21)

巷道顶部群锚杆以正方形格子布置。当锚杆横向和竖向之间的距离均小于2Ltan(45°-φ/2)时,群锚极限承载力由W′外=W′内推导得出：

(22)

4.2 帮部群锚极限承载力

由顶部群锚杆受力可知，帮部群锚的外力仅有锚杆拉力：

(23)

在剪切面上内部损耗功为：

(24)

巷道帮部群锚杆以正方形格子布置。当锚杆横向和竖向之间的距离均小于2Ltan(45°-φ/2)时,帮部群锚承载力由W′外=W′内推导得出：

(25)

5 现场监测与数值模拟分析

5.1 煤质指标

巷道顶、底板地层中粉砂岩与(砂质)泥岩组成见表1.

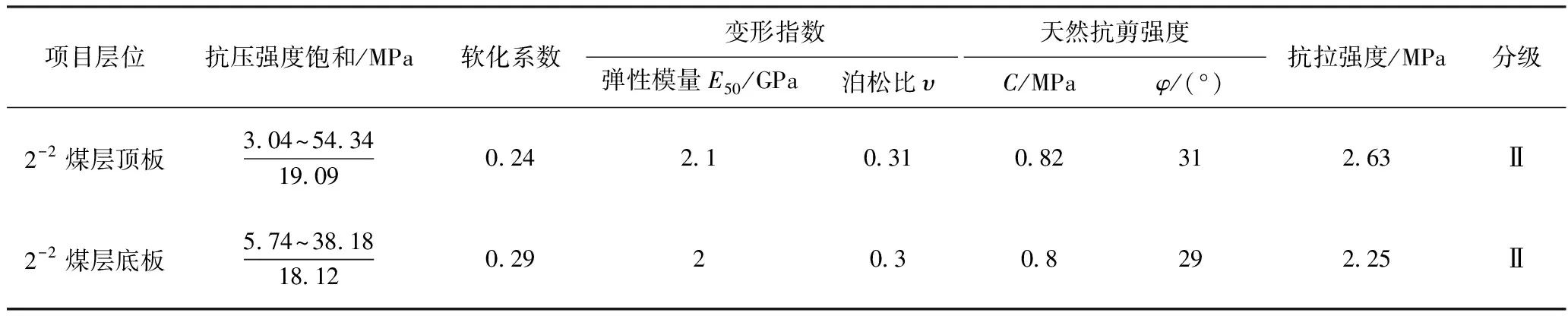
表1 顶、底板地质参数表

5.2 现场监测结果

由两组监测数据(图6、7)可知，当掘进面距离监测断面超过30 m时，随着掘进面的推进顶板离层量保持不变。断面1在1.5～2.0 m和2.5～3.0 mm处出现岩层分离，离层值分别为2.90 mm和2.00 mm，最大离层量为2.90 mm；断面2在1.5～2.0 m，3.0～4.0 m处出现离层，离层值分别为2.76 mm、2.05 mm.可推断出顶部锚固结构厚度大致在1.5～4.0 m，此范围锚固结构产生承载作用。

图6 S1231断面1顶板离层监测图

图7 S1231断面2顶板离层监测图

实测S1231辅运顺槽两帮离层变化曲线见图8、9，当掘进面距离监测面超过30 m时，两帮离层量不随掘进面的推进而变化。断面1开采帮离层位置发生在1.0～1.5 m，离层为1.67 mm；断面2非开采帮离层位置发生在1.0～1.5 m处，离层值为2.23 mm.可推断出帮部锚固结构在1.0～1.5 m，此范围锚固结构产生承载作用。

图8 S1231断面1开采帮离层监测图

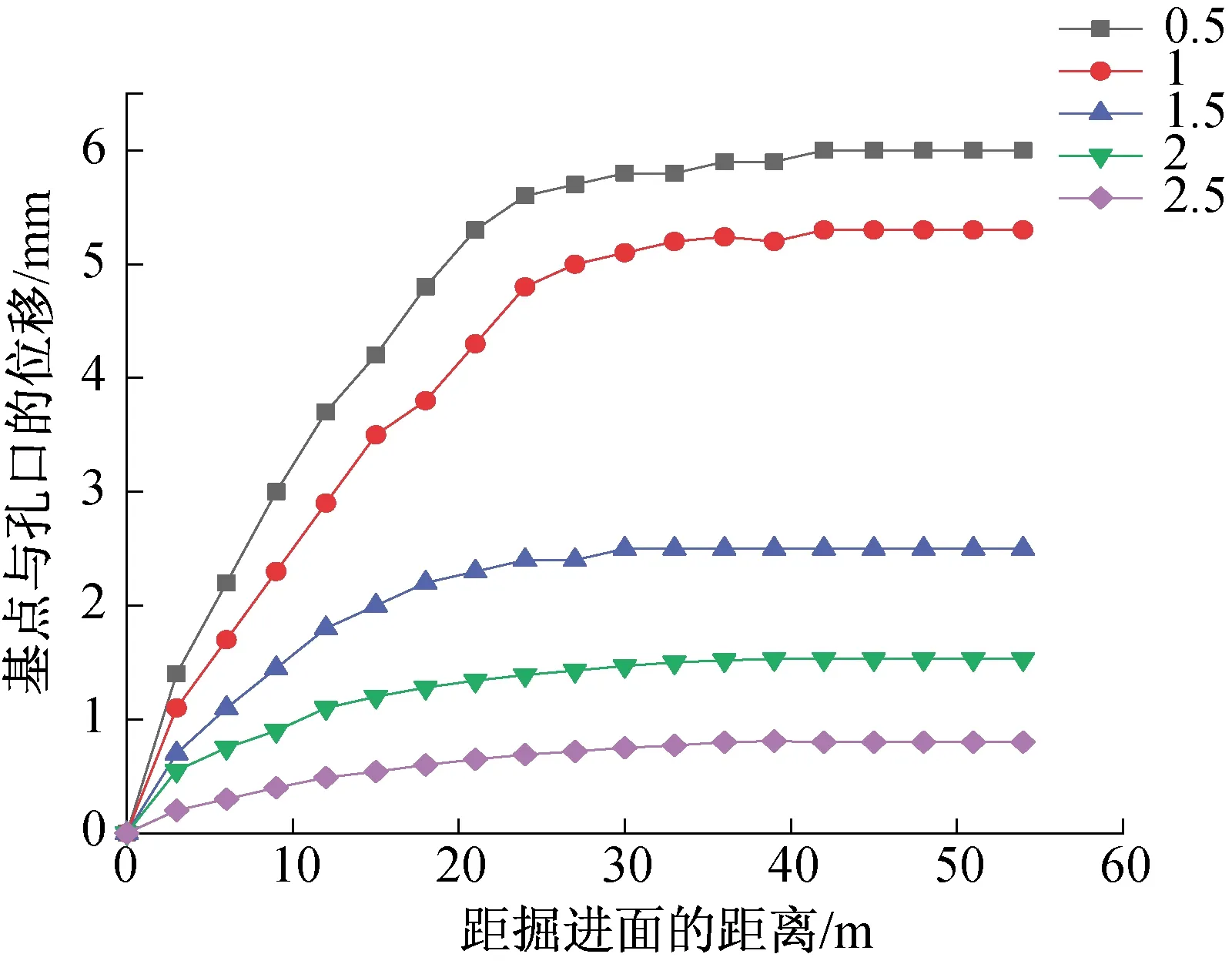
图9 S1231断面2开采帮离层监测图

5.3 数值模拟分析

通过数值模拟分别对塑性区分布图、应力云图以及围岩位移图进行分析计算，见图10，11，12.

由图10可知，采用传统锚杆支护和群锚支护时巷道顶板均未发生塑性区的延伸贯穿，均能保证巷道顶板安全稳定，但采用传统锚杆支护时围岩塑性区范围比群锚支护巷道更小。

由图11可知，采用锚杆支护方案时顶板竖向应力最小，采用群锚支护方案时顶板竖向应力大，说明传统锚杆支护方案比群锚支护在顶板中所受的支护力更小，造成支护过剩以及资源浪费。

图11 竖向应力分布图

由图12可知，在传统锚杆支护下巷道顶板最大下沉量为8.88 mm，在群锚支护下巷道顶板最大下沉量为14.13 mm，两种支护方案均能保证围岩安全稳定，但采用群锚支护时更加经济合理。

图12 竖向位移分布图

根据上限分析法理论对某煤矿辅运顺槽进行群锚支护设计，建立了数值计算模型。对现场实测的数据进行分析对比，得出以下结论：

1)通过原有支护方案和新支护方案监测对比，发现原有支护围岩变形较小，锚杆支护强度过大，锚杆长度较长造成资源浪费、施工周期长等，基于锚杆极限承载力力学模型计算，顶板锚杆长度设计为2.0 m，锚杆轴距为1 000 mm×1 000 mm，同样能够承受巷道围岩荷载，同时能够保证巷道安全可靠。

2)分析监测结果可知，在群锚支护方案下顶板最大下沉量为16.62 mm，两帮收敛大约为8.66 mm，锚杆最大轴力为40.52 kN，现场实测值与数值模拟计算值相差不大，符合支护设计要求。群锚支护方案不仅能够满足围岩使用要求，还能充分发挥自身承载性能，节约支护成本。

3)在顶板围岩表面不同位置处，沉降值并不相等，顶板中间部位沉降值最大，向顶板两帮逐渐递减；巷道顶板表面位移最大，向岩体深部逐渐减小；数值模拟所揭示的巷道顶板下沉变形规律与现场监测结果所反应出的规律一致。

6 结 论

1)在围岩性质与支护参数确定的情况下，对巷道整体稳定性做出评定；巷道在临界破坏时，能够判定破坏面的形状与范围等问题。此外，判定巷道围岩破坏的临界状态，工程界也存在着较大的争议；极限上限分析依据岩体破坏机制，推导出破坏场中内能耗散功率与外力功率并进行优化处理推导出能耗最小意义上的破坏荷载，简化了结构力学分析，从而优化了巷道支护设计方法，提高了巷道的施工水平，具有重要的工程使用价值。

2)不同围岩条件所对应的支护机理也不同，需选取符合相应工况的支护理论。根据锚杆支护作用原理，分析单锚和群锚支护围岩所形成不同破坏体的基础上，基于Mohr-Coulom强度理论和极限上线分析理论，建立了合理的力学模型，分析巷道围岩变形规律以及破坏机理，能够计算出群锚杆极限承载力；分析围岩岩体参数对巷道顶板锚杆极限承载力的影响，为巷道围岩长期稳定性评价提供依据。