计算机化分类测验终止规则的类别、特点及应用*

任 赫 黄颖诗 陈 平

·研究方法(Research Method)·

计算机化分类测验终止规则的类别、特点及应用*

任 赫 黄颖诗 陈 平

(北京师范大学中国基础教育质量监测协同创新中心, 北京 100875)

计算机化分类测验(Computerized Classification Testing, CCT)能够高效地对被试进行分类, 已广泛应用于合格性测验及临床心理学中。作为CCT的重要组成部分, 终止规则决定测验何时停止以及将被试最终划分到何种类别, 因此直接影响测验效率及分类准确率。已有的三大类终止规则(似然比规则、贝叶斯决策理论规则及置信区间规则)的核心思想分别为构造假设检验、设计损失函数和比较置信区间相对位置。同时, 在不同测验情境下, CCT的终止规则发展出不同的具体形式。未来研究可以继续开发贝叶斯规则、考虑多维多类别情境以及结合作答时间和机器学习算法。针对测验实际需求, 三类终止规则在合格性测验上均有应用潜力, 而临床问卷则倾向应用贝叶斯规则。

计算机化分类测验, 终止规则, 似然比, 随机缩减, 贝叶斯决策理论

1 引言

由于能够改变传统纸笔测验中相对固化的试题形式、更深刻地体现“因材施测”和“高效施测”, 计算机测验尤其是计算机化自适应测验(Computerized Adaptive Testing, CAT)近年来得到飞速发展。对于CAT而言, 其测验目的一般是准确估计被试能力, 而计算机化分类测验(Computerized Classification Testing, CCT)——作为CAT的一个重要分支——则以分类考生为目的。具体来说, CCT在CAT的基础上可以根据预设的分界分数将被试划分到两个(比如, 掌握和未掌握)或多个(比如, 合格、良好和优秀)不同的类别中。相比于传统纸笔测验, CCT的优势在于：首先, CCT不仅可以自适应地呈现最适合被试作答的题目, 还可以在保持相同决策精度的情况下大大缩短测验长度(Spray & Reckase, 1996), 进而降低测验成本、减少被试疲劳效应的影响; 其次, CCT依托于计算机施测的特点使其能够为被试呈现更加丰富的测验内容和题目形式(比如交互式测评), 并获取更多元细致的被试数据; 再者, CCT的高效计算力使得更精细测量模型和算法的使用成为可能, 比如融入过程性或多模态数据的模型(Sie et al., 2015; Zhan et al., 2021)以进一步满足各种测验需求、提升分类决策的可靠性。目前, CCT已经在合格性测验(比如, 职业资格考试)以及临床心理学或医学诊断(比如, 焦虑、抑郁等精神疾病的自我报告问卷和健康与护理问卷)中得到广泛应用(Finkelman et al., 2011; Huebner & Fina, 2015; Smits & Finkelman, 2013)。

作为CAT的特例, 完整的CCT同样包括心理测量模型、标定的题库、选题策略、能力参数估计方法以及终止规则五个核心部分。但是如前所述, 两者在测验目的上并不相同：CAT的目的是对被试能力进行准确估计(陈平, 2016), 而CCT是要对被试的类别进行准确划分。因此, 终止规则是区分CCT与CAT的一项主要特征(任赫, 陈平, 2021)。总体而言, CCT终止规则关注的核心问题是系统是否有足够的把握将被试划分到某个特定的类别, 或者说系统是否可以接受当前的决策结果(比如：继续测验、将被试划分到掌握/未掌握类别)可能产生的成本(如：测验效率的牺牲、第I类或第II类错误率)。由此, 终止规则决定测验何时停止以及将被试最终划分到何种类别, 将直接影响测验的效率和分类准确率。已有的CCT终止规则包括定长(fixed-length)的规则(即每名被试作答固定数量的题目)以及变长(variable-length)的规则(即每名被试作答数量不定的题目)。定长的规则比较简单, 不再赘述, 本文主要关注变长的规则。需要指出的是, 尽管定长终止规则的效率较低, 但是它可以保证所有被试作答相同长度的测验, 能够减少被试对测验公平的质疑, 主要应用于高利害测验中。与之相对应, 变长的规则具有高效的特点, 能够大大地缩短测验长度, 可以广泛应用于各类低利害测验中。

变长CCT的实施过程可以看作一种序贯抽样方案, 即“在抽样时不规定总的抽样个数, 而是根据已抽取的样本结果决定是否继续抽样, 直至停止”。最早的变长终止规则是Ferguson (1969)根据序贯检验(Wald, 1947)提出的序贯似然比方法(Sequential Probability Ratio Test, SPRT)。SPRT方法通过事先设定第I和第II类错误率来控制不同决策的损失, 并使用二项分布对被试作答进行建模, 相当于假设题库中所有题目的正确作答概率相同, 相应地以随机或固定顺序呈现题目。但是, Lewis和Sheehan (1990)则认为应该在测验过程中直接控制每一步可能造成的损失, 这就需要利用贝叶斯理论进行决策。另外, 为了使序贯抽样过程能够与被试能力相适应, Reckase (1983)与Kingsbury和Weiss (1983)分别引入项目反应理论(Item Response Theory, IRT)模型。前者使用IRT模型代替二项分布, 进而发展出允许自适应选题的SPRT方法(也即对Ferguson方法的改进), 而后者利用能力估计的置信区间进行分类决策。综上, 前人分别从不同的视角出发, 基于不同的统计学理论建构出三类终止规则, 它们分别是似然比规则、贝叶斯决策理论规则(后文简称贝叶斯规则)和置信区间规则(Ability Confidence Intervals, ACI)。

此外, 在构造具体的CCT终止规则时, 还需要考虑不同测验情境的特点, 主要包括被试的类别数和测验的维度数。在被试类别方面, 有时只需要将被试划分到两个不同类别, 而有时则需要将被试划分到三个及以上的不同类别, 它们分别对应于二分类的CCT与多分类的CCT。在测验维度方面, 一些测验只需要考虑被试在单个维度上的潜在特质, 但是更多的心理或教育测验往往需要同时考察被试在多个维度上的潜在特质(康春花, 辛涛, 2010), 这就分别对应于单维CCT (Unidimensional CCT, UCCT)与多维CCT (Multidimensional CCT, MCCT)。需要说明的是, 多分类的CCT终止规则在构造上与二分类的相比有较大差异, 而MCCT的终止规则通常可以由UCCT经过较为直接的推广而得到。

基于此, 本文将结合不同的测验情境, 对似然比规则、贝叶斯规则以及置信区间规则分别进行详细述评, 然后对各种规则的优劣进行讨论分析, 最后对CCT终止规则的未来研究方向及应用进行说明。

2 似然比规则

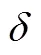
2.1 序贯似然比方法(SPRT)

2.1.1 二分类的SPRT方法

最早的二分类似然比终止规则就是Wald (1947)提出的SPRT。在此基础上, 研究者们主要致力于解决两个方面的问题：一是如何进一步提升二分类SPRT的决策效率; 二是如何将单维的二分类SPRT拓展到多维情境。对于第一个问题, Finkelman (2003, 2010)将随机缩减(stochastic curtailment)技术与SPRT方法相结合, 提出随机缩减的SPRT (Stochastically Curtailed SPRT, SCSPRT), 以进一步提高测验效率。需要指出的是, 上述方法仅适用于单维情境。对于第二个问题, 即将已有方法推广至MCCT时, 规则的构建思路基本没有变化, 但是能力参数的多维性会导致UCCT中的能力分界点转变为多维空间中的能力分界曲线或曲面(任赫, 陈平, 2021)。为此, Nydick (2013)从两个不同的角度解决这一问题, 分别提出约束的SPRT (Constrained SPRT, C-SPRT)以及使用空间投影方法构建的投影SPRT (Projected SPRT, P-SPRT)。另外, Nydick (2013)还在C-SPRT的基础上结合随机缩减技术开发出随机缩减的多维SPRT (Multidimensional SCSPRT, M-SCSPRT)。下文依次介绍单维的SPRT与SCSPRT以及多维的C-SPRT、P-SPRT与M-SCSPRT。

(1)单维的SPRT方法(SPRT与SCSPRT)

在UCCT中, SPRT使用一组简单假设来判断被试的能力分类, 即

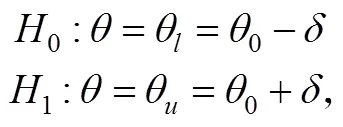
由此, SPRT (Wald, 1947)构造对数似然比统计量如下,

其中, 为基于IRT的似然函数, 为被试在题目上的作答向量。记第Ⅰ类、第Ⅱ类错误率分别为和, 令、、、(Finkelman, 2003)。被试完成道题目后, 计算对数似然比统计量, 并按如下规则对被试给出判断：若, 则考生的分数更有可能低于分数线, 判断被试属于“未掌握”, 并结束测验, 记测验长度为; 若, 则考生的分数更有可能高于分数线, 判断被试属于“掌握”, 并结束测验, 记测验长度为; 否则, 要求被试继续作答下一道题。例如, 图1展示了使用两参数逻辑斯蒂克模型模拟数据得到的“不同能力取值下的对数似然函数值”, 当分界分数取、、时, 得到、、、。此时, , 于是计算得到对数似然比统计量 。由于<, 所以继续测验。

(2)多维的SPRT方法(C-SPRT、P-SPRT与M-SCSPRT)

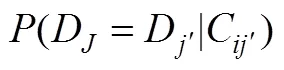
2.1.2 多分类的SPRT方法

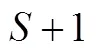
图2 一个三分类问题的示意图

(1)Sobel-Wald方法

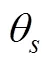
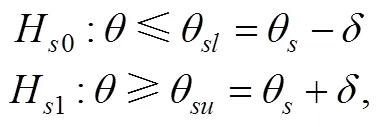
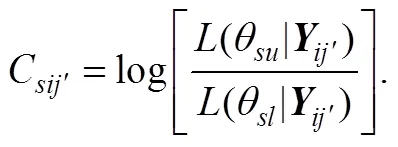
(2)Armitage方法

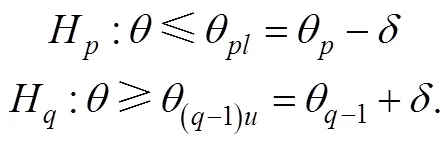
对应的检验统计量为,

需要说明的是, 只有当Sobel-Wald方法无法给出准确的分类判断时, 其与Armitage的方法才存在差异(Wang et al., 2021)。而在大多数情况下, 这两种方法所得到的结果都一致, 但是Armitage方法需要进行更多次检验。Wang等人(2021)的研究中使用一个四分类问题为例, 对其进行理论分析, 感兴趣的读者可以参阅。也就是说, Sobel和Wald方法在测验的分类准确率上应与Armitage方法相近, 但在测验效率上应更胜一筹, 这与已有研究的结果一致(Govindarajulu, 1987; Ghosh & Sen, 1991)。

2.2 广义似然比方法(GLR)

在SPRT中, 最大测验长度的使用可能会降低分类准确率。为此, Bartroff等人(2008)将GLR应用于UCCT。之后, 研究者又将随机缩减技术与GLR相结合, 提出随机缩减的GLR方法(Stochastically Curtailed GLR, SCGLR; Huebner & Fina, 2015)。另外, Nydick (2013)也将GLR方法推广到多维情境中, 提出多维的广义似然比方法(MultidimensionalGLR, M-GLR)。

2.2.1 二分类的GLR方法

(1)单维的GLR方法(GLR与SCGLR)

不同于SPRT方法使用一组简单假设(即公式(1)), GLR使用下述的一组复合假设对被试进行分类判断,

(2)多维的GLR方法

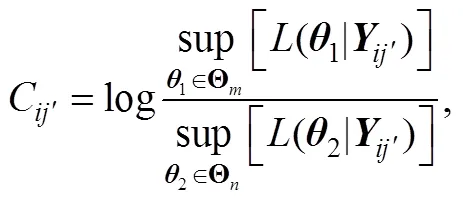
2.2.2 多分类的GLR方法

由此, Wang等人(2021)指出可以根据序贯分析中的多假设GLR检验(Tartakovsky et al., 2014), 为上述复合假设构造如下的多分类GLR统计量

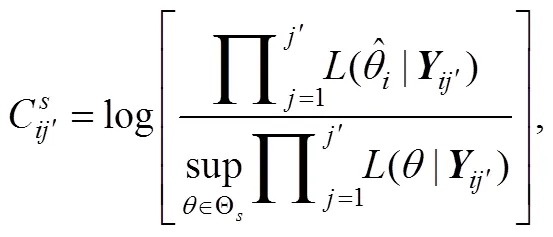
2.3 似然比规则简评

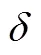
3 贝叶斯决策理论规则

贝叶斯规则是另一类重要的CCT终止规则。不同于蕴含假设检验的规则, 贝叶斯规则以贝叶斯决策理论为基础, 通过定义后验概率与损失函数, 就可以选择期望损失最小的决策以完成对被试的分类判断。其中, 损失由错误决策所产生, 具体可分为阈值损失和线性损失。目前为止, 研究者对贝叶斯规则的研究基本仍限于UCCT情境。

3.1 阈值损失

(1)二分类的阈值损失规则

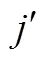
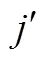
表1 阶段时的二分类阈值损失函数

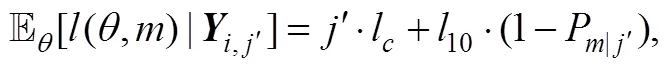
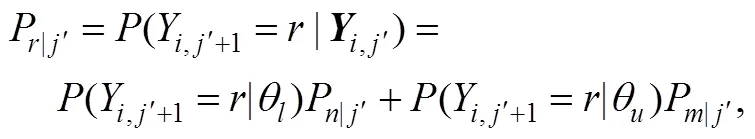
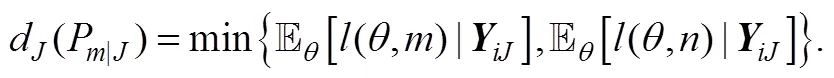
在时, 还需要考虑继续作答的损失。此时, 根据上式就可以依次迭代, 得到测验在达到最大长度之前继续作答的期望损失。比如, 如图3所示, 对于二级计分的题目, 在时, 被试分别以和的概率答错或答对下一题(第题)。被试作答第题后, 由于达到最大测验长度, 只需要做出分类决策而不需要继续作答, 所以此时的风险函数就如同等式(20)。

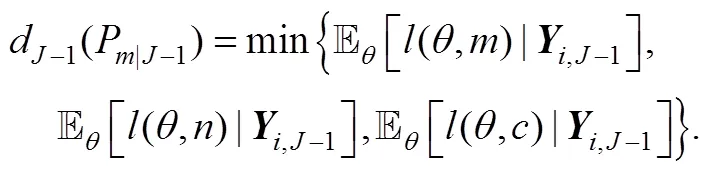
根据上式就可以对被试进行分类判断。具体地说, 系统将选择使得期望损失最小的决定(将被试划分为掌握, 未掌握或要求继续作答), 即

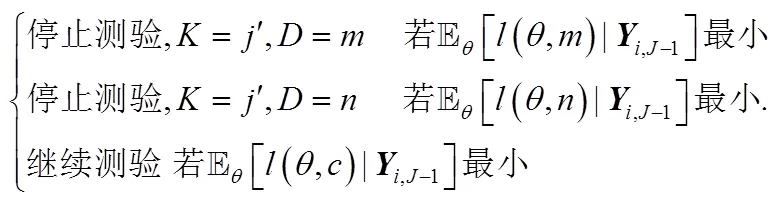
(2)多分类的阈值损失规则

对于贝叶斯规则而言, 从二分类到多分类的推广比较简单。对于一个三分类的UCCT, 只需要将表1中的阈值损失函数替换为表2中内容, 再选择最小的损失即可完成对被试的分类判断(Vos, 1999)。

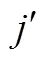
表2 阶段的三分类阈值损失函数

3.2 线性损失

表1中的阈值损失函数具有一个明显的缺点：它假定对于不同能力值的被试的损失是恒定的, 而不考虑这些被试能力值与分界分数的距离。但事实上, 能力值离分界分数更远的被试被错误分类所造成的损失往往更严重。此外, 阈值损失函数的值也不是连续变化的, 这在很多情况下也不符合现实。因此, 一种更合理的假设是：损失函数是关于能力与分界分数间距离的连续增函数(van der Linden & Mellenbergh, 1977; van der Linden & Vos, 1996; Vos, 1997a, 1997b)。

(1)二分类的线性损失规则

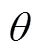
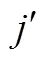
表3 阶段的二分类线性损失函数

(2)多分类的线性损失规则

与阈值损失函数类似, 在多分类情境下, 只需要将表3中的线性损失函数替换成表4中的内容即可得到一种三分类的线性损失函数(Vos, 1999)。

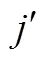
表4 阶段的三分类线性损失函数

3.3 贝叶斯规则简评

贝叶斯规则所提供的思路与似然比规则的完全不同。似然比规则是通过构造似然比统计量进行假设检验, 贝叶斯方法则是通过作答更新被试能力的后验分布, 并使用后验概率计算损失函数值, 从而基于贝叶斯决策论完成对被试的判断。

需要指出的是, 在贝叶斯规则中, 有无数种可能的损失函数, 没有哪一种损失函数一定是最好的。这一特点既是贝叶斯规则最大的优点, 也是其饱受诟病的一点。支持者认为这使得该方法能够考虑多样的损失函数, 具有更大的灵活性; 但是, 反对者认为损失函数的选择具有一定程度的任意性。在使用该方法之前, 研究者需要考虑清楚如何客观、科学地选择需要的损失函数。

4 置信区间规则

除似然比规则和贝叶斯规则外, CCT终止规则中还有一种是ACI方法。ACI方法通过比较分界分数与“被试能力估计值的置信区间”的相对位置, 来完成对被试的分类判断。

4.1 置信区间规则介绍

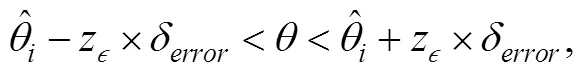
4.2 置信区间规则简评

在某种程度上, 可以认为ACI方法将被试的分类问题转化为被试的能力估计问题。这样做的好处是使得对被试的分类变得非常直观、简洁。但是, 这种方法的稳健性相对较差。因为使用该方法需要有足够大的标定题库作为前提, 否则就可能会导致较高的错误率。同时, Eggen和Straetmans (2000)以及Thompson (2009)的研究都表明：该方法所需的测验长度一般高于似然比规则。

5 三类终止规则的综合分析

5.1 三类终止规则的构造思路与优缺点分析

综上所述, 三类终止规则各有优缺点。其中, 似然比规则基于似然比检验, 具有较好的理论性质, 大多数测验情境下最为准确、高效, 相关研究也较多。但是, 由于需要定义无差别区间大小和第I、第II类错误率, 引入了主观因素的影响, 并且该方法在多维、多分类等复杂测验情境下的拓展难度较大。已有的多分类SPRT终止规则(Sobel-Wald方法与Armitage方法)是对多个能力分界点独立进行假设检验, 因此会隐含多重比较的问题, 即实际的第Ⅰ和第Ⅱ类错误率远大于设定标准。尽管已有研究者留意到这一点(Wang, 2019; Wang et al., 2021), 但由于第I和第II类错误率的变化并不是影响SPRT规则的分类准确性的主要因素, 所以较少有研究对其进行校正。

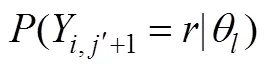
ACI方法直接将分界分数与能力估计值的置信区间进行比较, 无需划定无差别区间, 并且计算简单且计算量小, 是三种方法中最直接的一类方法。但是, 这种方法的稳健性较差, 测验效率也相对较低。表5是对上述各种方法的总结。

5.2 三类终止规则的适用情境

需要指出的是, CCT是一个非常复杂的测验系统。终止规则的优劣还会受到CCT中其他部分(比如, 心理测量模型、题库结构和选题策略)以及被试能力分布等因素的影响, 三类终止规则在不同的测验情境下各占鳌头。因此, 实践者在选择终止规则时需要综合考虑CCT的各个部分以明确三类终止规则的适用情境。另外, 还需要注意相应情境下可能面临的现实问题。

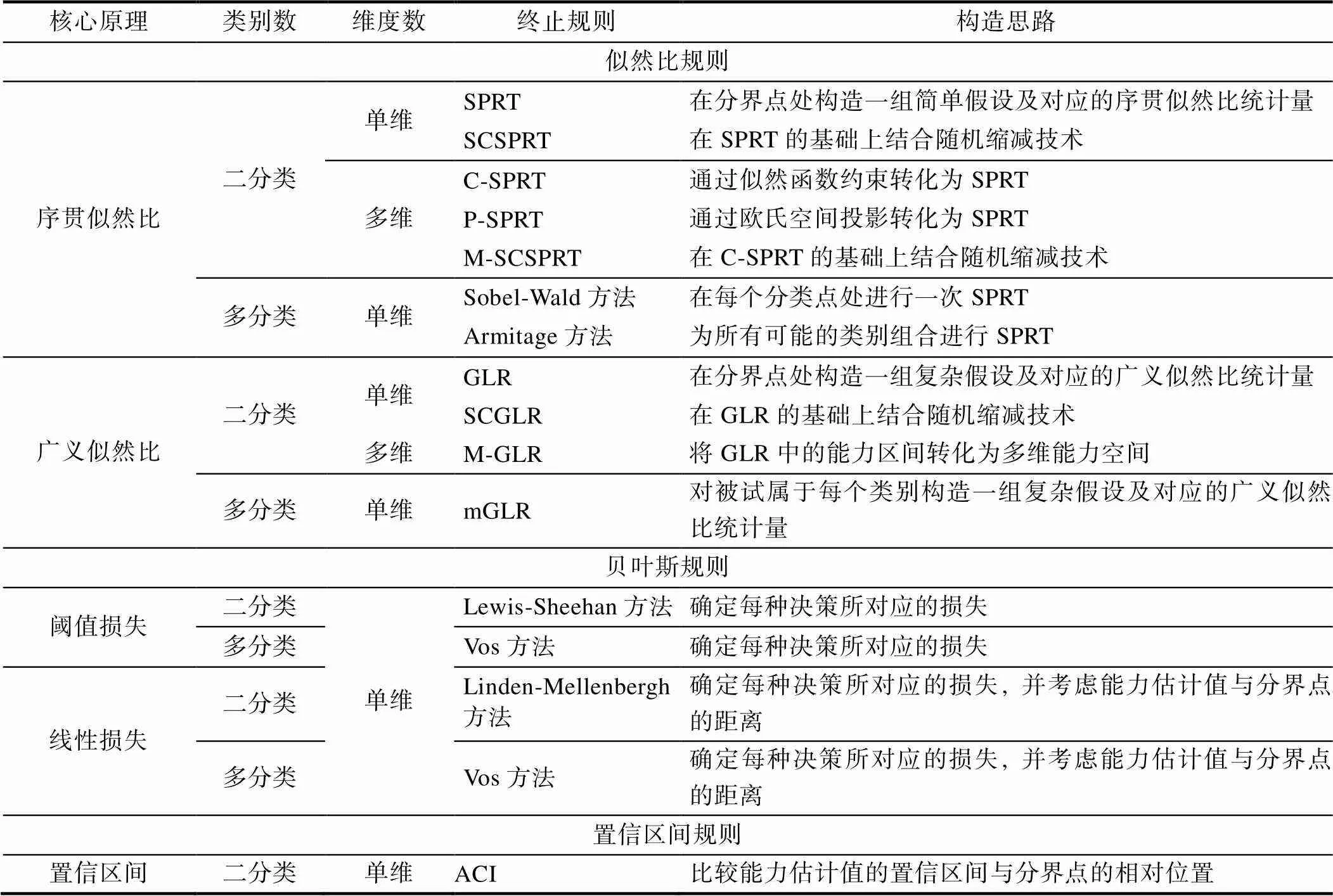
表5 CCT终止规则的总结

对于似然比规则, 想要准确且快速做出决策的关键在于最大程度地区分不同类别被试的似然函数值, 而这通常和选题策略密切相关。举例而言, 在UCCT中, 两种常见的选题策略是基于能力估计值的最大信息量选题方法(estimate-based maximum Fisher information)和基于分界分数的最大信息量选题方法(cutscore-based maximum Fisher information)。因此, 当选题策略为后者时, 所选的题目能够为假设检验提供更多的信息, 因此似然比规则在基于分界分数的最大信息量选题方法下的效率最高。但是由于基于分界分数会因为固定点选题而导致题目高曝光的问题, 所以似然比规则更适用于低风险的测验, 而且要求题库中大部分题目在分界分数处具有高信息量。此外, 由于GLR考虑无差别区间两侧的所有对数似然函数值(不仅着眼于上、下界两个点), 所以相比于SPRT, GLR在基于当前能力估计选题时也能保持一定的效率。

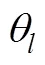
对于置信区间规则, 保障决策效率的关键在于不断地减小能力估计标准误。因此, ACI方法在基于能力估计值的最大信息量选题方法下的效率最高, 该选题策略可以减小置信区间的大小。此外, 根据不同被试的能力, ACI规则能够为不同被试呈现不同的题目, 在一定程度上能降低高信息量题目的曝光率, 所以它可以用于高风险的测验, 相应地需要题库中的题目在不同能力位置具有高信息量。但是Tian (2018)在控制分类准确性一致的前提下, 采用基于能力估计值的选题方法, 比较单维二分类的似然比规则和置信区间规则。结果发现：当被试能力分布远离分界分数时, ACI规则的效率要高于似然比规则; 但是在被试能力分布靠近分界分数时, ACI规则效率低于GLR方法。这意味着ACI规则的表现还会受到被试能力分布与分界分数相对位置的影响, 因此更适用于要求高通过率或低通过率的测验。

6 未来研究方向及应用

6.1 CCT终止规则的未来研究方向

本文对多种测验情境下的CCT终止规则进行系统梳理与述评。目前, 对CCT终止规则的研究已经比较丰富, 但仍有一些地方有待完善。未来研究方向主要表现在以下四方面：

(1)完善基于贝叶斯的终止规则。构建CCT终止规则的思路主要有三个角度, 即似然比方法、贝叶斯方法和置信区间方法。基于似然比方法的终止规则已经得到充分的发展, 但如前所述, 以贝叶斯方法为基础的终止规则仍然较少。未来, 研究者可以考虑基于贝叶斯方法对前人研究进行完善。例如, 在现实测验情景中, 除考虑决策的准确率和测验长度之外, 还需要满足其他非统计约束(如：内容均衡, 即让试卷充分涵盖所要考察的知识模块)。由于贝叶斯损失函数具有灵活性, 研究者可以考虑将各种非统计约束纳入终止规则的考虑范围。此外, 正如5.1部分所言, 目前贝叶斯方法没有利用已有的信息对被试即将作答的下一道题进行预测, 未来研究可以借鉴似然比方法中随机缩减的思想来构造一组“合适”的题目替代被试未来实际作答的题目。最后, 研究者还可以对损失函数中损失值的选取如何影响测验结果进行讨论。

(2)开发多维多分类的CCT终止规则。多维或多分类的CCT终止规则是近期的一个研究热点, 但尚未有研究者探究同时满足多维、多分类要求的CCT终止规则。在现实应用中, 许多测验不仅要同时考察被试在多个维度上的潜在特质, 而且也需要将被试分到多于两个的类别中。例如, 教育工作者希望将学生的数学成就水平划分为基础、熟练和高级三个类别(比如, 美国国家进步教育评估NAEP); 而数学测验也往往同时考察学生的算术、阅读和问题解决能力等, 呈现出多维的能力结构(Reckase, 2009)。这就对构建多维、多分类的CCT终止规则提出迫切需求。

(3)开发融合作答时间(Response Time, RT; 詹沛达等, 2020)的CCT终止规则。近几年来, 心理测量学的研究重点大都放在如何同时衡量多个维度的潜在特质, 以向被试提供更详细、更完善的反馈。但是这些研究大多只考虑被试的作答信息, 而很少使用行为信息。在CCT测验中, 有一类很容易获得的行为信息, 即被试作答所用的时间。Sie等人(2015)尝试构建融入RT的CCT, 他们的研究结果表明：融入RT后, 测验在分类精度轻微提高的同时还能够减少平均测验时间。但是, Sie等人(2015)的研究主要集中在限制被试作答时间, 而未考虑更普遍的限制测验长度的情况。未来, 研究者可以在上述研究的基础上进一步展开探索, 开发新的结合RT的CCT终止规则, 在保持判断准确率的基础上缩短测验长度, 而不仅仅是控制测验时间。另外, 可以考虑如何利用作答时间提高分类决策的精度, 进而间接提高测验效率(Man et al., 2019; 詹沛达, 2019)。

(4)开发结合机器学习算法的CCT终止规则。目前的三类终止规则均为基于心理测量模型的方法, 模型的正确设定和前提假设的满足对结果有重要的影响, 然而实践中的数据往往掺杂着各式各样的噪音。机器学习是近年来各个领域研究的热点, 其中许多算法都是用来解决分类问题, 这与CCT的目的相一致。Gonzalez (2021)认为, 相比于比较“通过各种模型估计得到的被试能力”与“黄金标准”来获得被试的类别, 机器学习算法通过被试的作答就能直接预测被试属于某个类别的概率, 避免模型不拟合等引起的误差。Zheng等人(2020)基于机器学习算法中的决策树方法, 开发出一个短的基于树的自适应分类测验。未来, 研究者可以考虑使用其他的分类算法(比如, 逻辑斯蒂克回归、支持向量机以及随机森林等方法)完成自适应分类测验。

6.2 CCT终止规则的应用

CCT测验主要包含两种类型：合格性测验与临床医学问卷。在为不同类型的测验制定终止规则时, 应充分考虑测验的考生群体、试题特点以及决策影响。

在合格性测试中, 通过设置不同难度的试题, 将考生划分到不同能力水平, 根据考生的等级水平, 来决定其从业资格、学业进度或升学。许多职业资格考试都属于这类测验, 比如教师资格考试、司法考试和执业医师资格考试等; 此外, 还有一些学业水平考试也属于合格性测验, 比如大学英语四、六级考试、计算机二级考试以及初中学业水平测试等。对于此类测验, 往往每年均有数量庞大的考生群体, 具有充足的测验经费和考生样本, 相应地能够建立起一定规模的题库, 并在一定程度上能保障题目参数的稳定估计, 使得合格性测验具有运用三类终止规则的潜力。但是, 似然比规则与贝叶斯规则的原理较为复杂, 且正如5.2部分所言, 这些方法在实践中伴随着题目曝光率过高的问题。因此, 在现有的合格性测验尤其是高风险的合格性测验中, 鲜有这两类方法的应用。与上述两种规则的困境形成对比的是, 置信区间规则原理简明易懂、分类结果清晰, 更能为大众和教育工作者所理解, 更具有推广性, 在现实中就显得更加可行。比如, 美国联合委员会注册护士执照考试(the National Council LicensureExamination for Registered/Practical Nurse, NCLEX- RN)就使用ACI规则来决定测验何时终止。

在临床医学问卷中, 通过评价患者在不同指标上的轻重程度或近期的心理生理状态, 将患者划分到不同症状水平, 来为其后续的治疗和诊断提供依据。比如, 汉密尔顿抑郁量表(Hamilton Rating Scale for Depression, HRSD)和创伤后应激障碍量表(Posttraumatic Stress Disorder Checklist, PCL)。对于此类测验, 被试群体往往很小, 且问卷的题项并不具有一般意义上的难度。更重要的是, 假阴性(false negative)的分类结果所带来的代价不可忽视。因此, 考虑到相比于另外两类终止规则, 贝叶斯终止规则能够对各种分类损失有更精细的控制, 在临床医学问卷中更为适用。目前, 终止规则在临床医学问卷中的应用目的主要为：在保证决策准确基础上缩短已有问卷的长度, 使得诊断过程更高效, 比如利用机器学习模型或随机缩减技术进一步缩减问卷长度(Gonzalez, 2021; Smits et al., 2016)。还需要注意的是, 临床问卷以往直接使用观测分数与诊断临界值相比较, 而已有的终止规则主要基于潜在特质进行计算。但随着IRT研究的推进, 越来越多的研究者使用IRT模型对临床问卷建模, 比如Li等人(2019)将等级反应模型(Graded Response Model, GRM)应用于病人健康问卷(the Patient Health Questionnaire, PHQ)。因此, 相比于Smits等人(2016)使用基于观测分数的CCT并选择随机缩减的倒计时法(countdown method)作为终止规则, 贝叶斯规则或许既能够缩短测验长度, 又能在每一步中严格控制诊断的损失。

陈平. (2016). 两种新的计算机化自适应测验在线标定方法.(9), 1184–1198.

简小珠, 陈平. (2020). 计算机化分类测验的特点与发展述评.(6), 77–89.

康春花, 辛涛. (2010). 测验理论的新发展:多维项目反应理论.(3), 530–536.

任赫, 陈平. (2021). 两种新的多维计算机化分类测验终止规则.,(9)1044–1058

詹沛达. (2019). 计算机化多维测验中作答时间和作答精度数据的联合分析., (1), 170–178.

詹沛达, Hong Jiao, Kaiwen Man. (2020). 多维对数正态作答时间模型：对潜在加工速度多维性的探究., 1132–1142.

Armitage, P. (1950). Sequential analysis with more than two alternative hypotheses, and its relation to discriminant function analysis.(1), 137–144.

Bartroff, J., Finkelman, M., & Lai, T. L. (2008). Modern sequential analysis and its applications to computerized adaptive testing.(3), 473–486.

Eggen, T. J. H. M. (1999). Item selection in adaptive testing with the sequential probability ratio test.(3), 249–261.

Eggen, T. J. H. M., & Straetmans, G. J. J. M. (2000). Computerized adaptive testing for classifying examinees into three categories.(5), 713–734.

Ferguson, R. L. (1969).(Working Paper No. 41). Pittsburgh, PA: University of Pittsburgh, Learning and Research Development Center.

Finkelman, M. (2003).(CSE Report 606). Los Angeles, CA: National Center for Research on Evaluation, Standards, and Student Testing.

Finkelman, M. (2008). On using stochastic curtailment to shorten the SPRT in sequential mastery testing.(4), 442–463.

Finkelman, M. (2010). Variations on stochastic curtailment in sequential mastery testing.(1), 27–45.

Finkelman, M., He, Y., Kim, W., & Lai, A. M. (2011). Stochastic curtailment of health questionnaires: A method to reduce respondent burden.(16), 1989–2004.

Ghosh, B. K. (1970).. Reading, MA: Addison-Wesley.

Ghosh, B. K., & Sen, P. K. (1991).. New York, NY: Marcel Dekker.

Gonzalez, O. (2021). Psychometric and machine learning approaches for diagnostic assessment and tests of individual classification.(2), 236–254.

Govindarajulu, Z. (1987).Columbus, OH: American Sciences Press, Inc.

Huang, C.-Y., Kalohn, J. C., Lin, C.-J., & Spray, J. (2000).(Research Report 2000-4). Iowa City, IA: ACT, Inc.

Huebner, A. R., & Fina, A. D. (2015). The stochastically curtailed generalized likelihood ratio: A new termination criterion for variable-length computerized classification tests.(2), 549–561.

Kingsbury, G. G., & Weiss, D. J. (1983). A comparison of IRT-based adaptive mastery testing and a sequential mastery testing procedure. In D. J. Weiss (Ed.),(pp. 257–283). New York, NY: Academic Press.

Lewis, C., & Sheehan, K. (1990). Using Bayesian decision theory to design a computerized mastery test.(4), 367–386.

Li, C., Moore, S. C., Smith, J., Bauermeister, S., & Gallacher, J. (2019). The costs of negative affect attributable to alcohol consumption in later life: A within-between random longitudinal econometric model using UK Biobank.(2), Article e0211357. https://doi.org/10.1371/journal. pone.0211357

Man, K., Harring, J. R., Jiao, H., & Zhan, P. (2019). Joint modeling of compensatory multidimensional item responses and response times.,(8), 639–654.

Nydick, S. (2013).(Unpublished doctoral dissertation). University of Minnesota.

Reckase, M. D. (1983). A procedure for decision making using tailored testing. In D. J. Weiss (Ed.),(pp. 237–257). New York, NY: Academic Press.

Reckase, M. D. (2009).. New York, NY: Springer.

Seitz, N.-N., & Frey, A. (2013). The sequential probability ratio test for multidimensional adaptive testing with between-item multidimensionality.(1), 105–123.

Sie, H., Finkelman, M. D., Riley, B., & Smits, N. (2015). Utilizing response times in computerized classification testing.(5), 389–405.

Smits, N., & Finkelman, M. D. (2013). A comparison of computerized classification testing and computerized adaptive testing in clinical psychology., 19–37.

Smits, N., Finkelman, M. D., & Kelderman, H. (2016). Stochastic curtailment of questionnaires for three-level classification: Shortening the CES-D for assessing low, moderate, and high risk of depression.(1), 22–36.

Sobel, M., & Wald, A. (1949). A sequential decision procedure for choosing one of three hypotheses concerning the unknown mean of a normal distribution.(4), 502–522.

Spray, J. A. (1993).(ACT Research Report Series, No. 93-7). Iowa City, IA: Americn College Testing.

Spray, J. A., & Reckase, M. D. (1996). Comparison of SPRT and sequential Bayes procedures for classifying examinees into two categories using a computerized test.(4), 405–414.

Tartakovsky, A., Nikiforov, I., & Basseville, M. (2014).. Boca Raton, FL: Chapman and Hall/CRC.

Thompson, N. A. (2009). Item selection in computerized classification testing.(5), 778–793.

Thompson, N. A. (2011). Termination criteria for computerized classification testing.(4), 1–7.

Tian, C. (2018).(Unpublished master’s thesis). University of Illinois.

van der Linden, W. J., & Mellenbergh, G. J. (1977). Optimal cutting scores using a linear loss function.(4), 593–599.

van der Linden, W. J., & Vos, H. J. (1996). A compensatory approach to optimal selection with mastery scores.155–172.

van Groen, M. M., Eggen, T. J. H, M., & Veldkamp, B. P. (2014). Item selection methods based on multiple objective approaches for classifying respondents into multiple levels.(3), 187–200.

Vos, H. J. (1997a). Simultaneous optimization of quota- restricted selection decisions with mastery scores.(1), 105–125.

Vos, H. J. (1997b). A simultaneous approach to optimizing treatment assignments with mastery scores.(4), 403–433.

Vos, H. J. (1999). Applications of Bayesian decision theory to sequential mastery testing.(3), 271–292.

Wald, A. (1947).. New York, NY: John Wiley.

Wald, A., & Wolfowitz, J. (1948). Optimum character of the sequential probability ratio test., 326–339.

Wang, C., Chen, P., & Huebner, A. (2021). Stopping rules for multi-category computerized classification testing.(2), 184–202

Wang, Z. (2019).(Unpublished doctoral dissertation). University of Minnesota.

Zhan, P., Jiao, H., Man, K., Wang, W.-C., & He, K. (2021). Variable speed across dimensions of ability in the joint model for responses and response times., Article 469196. https://doi.org/10.3389/ fpsyg.2021.469196

Zheng, Y., Cheon, H., & Katz, C. M. (2020). Using machine learning methods to develop a short tree-based adaptive classification test: Case study with a high-dimensional itempool and imbalanced data.(7–8), 499–514. https://doi.org/10.1177/0146621620931198

Types, characteristics and application of termination rules in computerized classification testing

REN He, HUANG Yingshi, CHEN Ping

(Collaborative Innovation Center of Assessment for Basic Education Quality, Beijing Normal University, Beijing 100875, China)

Computerized classification testing (CCT) has been widely used in eligibility testing and clinical psychology for its efficiency in classifying participants. As an essential part of CCT, the termination rule determines when the test is to be stopped and what category the participants are ultimately classified into, directly affecting the test efficiency and classification accuracy. According to the theoretical basis of the termination rules, existing rules can be roughly divided into the likelihood ratio, Bayesian decision theory, and confidence interval rules. And their core ideas are constructing hypothesis tests, designing loss functions, and comparing the relative positions of confidence intervals, respectively. Based on these ideas, in different test situations, CCT termination rules have various specific forms. Future research can further extend Bayesian rules, construct rules for multidimensional and multicategory CCT, integrate process data into termination rules, and build rules under the framework of machine learning. In addition, from the perspective of practical requirement, all three types of rules have the potential to be applied in eligibility tests, while the Bayesian rules are optimal to clinical questionnaires.

computerized classification testing, termination rule, likelihood radio, stochastic curtailment, Bayesian decision theory

2021-06-18

* 国家自然科学基金面上项目(32071092)、中国基础教育质量监测协同创新中心基础教育质量监测科研基金项目(2019-01-082-BZK01和2019-01-082-BZK02)资助。

陈平, E-mail: pchen@bnu.edu.cn

B841