随机森林在红松活立木腐朽分级中的应用1)
谢军明 王立海 林文树 郝泉龄 解光强 孟庆凯 李怡娜 阚相成
(东北林业大学,哈尔滨,150040)
树木内部腐朽是常见的一种缺陷,腐朽病的发生不仅对树木自身生长及木材使用存在危害,且其危害严重时对森林公园的旅游活动也有一定程度的安全隐患,降低森林旅游资源的价值[1]。因此,根据无损检测技术并联合智能算法对活立木腐朽程度进行分级,有利于监测活立木的健康情况,可对森林公园林木健康情况进行及时有效的干预,同时对林木防护也具有重要意义。
目前,利用无损检测手段并结合智能算法对活立木腐朽分级的研究较少。刘国荣等[2]将树干解析为木圆盘,以圆盘腐朽面积占总面积之比,将腐朽程度划分为5个等级。段新芳等[3]采用应力波测定仪对西藏古建筑上的腐朽与虫蛀木构件进行无损检测和目测腐朽观察,分析健康材和腐朽材的应力波传播速度,确定表层腐朽分级与无损检测结果基本一致。梁善庆[4]根据应力波断层图像,利用腐朽断面中剩余健康材径向厚度与树干半径的比值对树干进行危险性定量评价,将其分为无危险,警惕,危险3个级别。Yue et al.[5]使用应力波断层扫描仪及电阻断层成像仪对水曲柳、小叶杨进行检测,根据其成像特征将木材腐朽严重程度分为2个阶段:早期阶段、晚期阶段。以上研究均是根据无损检测或目测方式对立木腐朽进行分级,其效率低且还需有丰富经验的人员。对此,郝泉龄等[6]根据无损检测指标建立逻辑回归模型预测腐朽等级,但其准确率不高。因此,需探寻一种更好的模型提高立木腐朽分级的准确率。
机器学习算法用以解决立木腐朽分级问题,对判定树木健康情况提供了一种新的思路和方法,其最初由无监督分类方法(聚类、稀疏自编码、限制玻尔兹曼机等)发展到监督分类方法(逻辑回归、支持向量机、决策树等),准确率不断提高,分类效果越来越显著[7]。目前这些方法存在一些不足之处,逻辑回归分类方法容易欠拟合且其分类精度不高[8];支持向量机的决策边界易受不平衡数据集影响;决策树容易过拟合[9];无监督分类方法则需要大量的样本或对分类类别难以控制。因此,需要探索更稳定,更适用的机器学习方法来处理立木腐朽程度的分级问题。
随机森林是由许多决策树组合而成的一种机器学习算法,其保留决策树的优点,克服其缺点,同时可以提高分类的精度,并具有处理类不平衡数据的能力,其优越的性能在医学、食品、农林等众多领域广泛使用[10-14]。综上所述,本研究拟将随机森林用于腐朽分级中,以无损检测数据构建随机森林模型,对活立木的健康状况进行监督分类,同时与逻辑回归,支持向量机,决策树算法进行比较,依据腐朽分级评价指标的有效性,将活立木健康状况的预测值与实测值进行分析比较,判断模型的稳定性及可靠性,为立木腐朽分级判别提供一种方法。
1 研究区概况
五营森林公园位于黑龙江省伊春市五营区(129°6′~129°30′E,47°54′~48°19′N),森林公园总面积14 141 hm2,森林覆盖率89.2%,有亚洲面积最大的红松林,该地区地势平缓,平原较少,属低山丘陵地带,以暗棕色森林土壤为主;属温带大陆性湿润季风气候,年平均气温为0.6 ℃,年平均降水量为609.6 mm[15]。
2 研究方法
2.1 试验数据
选取五营森林公园红松原始森林带中不同腐朽程度的30棵红松,在距离地面130 cm立木横截面上,用阻抗仪和电阻断层成像仪对红松进行检测,在其检测的邻近部位用树木生长锥钻取2~3根腐朽或健康的木芯,将其放置于密封袋中带回实验室,使用烘干箱烘干,测量木芯质量损失率[16]。
本研究应用随机森林模型对立木腐朽进行分级建模,其中选取的研究对象为国家二级重点保护植物红松,为了不影响红松内部组织及其今后的正常生长,所以在选取自变量时应该优先选择无损,易获取及与立木腐朽相关的变量。在活立木检测中,阻抗仪和电阻断层成像仪(ERT)是常用的无损检测设备,2种设备能初步反映出腐朽立木的力学和电学性能变化,为立木腐朽的定性及定量提供方法[6,17],并且由这2种无损检测设备分析处理得来的数据(阻力损失,心材、边材异常面积比)在一定程度能反映出立木腐朽情况,因此选择这3个无损检测指标作为自变量。其中,用阻力的下降幅度定义阻力损失,阻力损失代表立木内部的力学性能损失程度,其与腐朽程度变化趋势一致;心材、边材异常面积比是依据健康与腐朽立木中心材与边材的电阻断层图像存在的明显颜色差异,通过提取像素方法将其划分为2个区域(心材与边材),并分别计算各区域异常像素比。心材、边材异常面积比反映了腐朽立木截面处的心材、边材与健康立木间存在的异常,其异常程度越高,代表腐朽越严重。
目前对于活立木腐朽分级标准没有统一的标准,部分研究以木芯质量损失率作为立木腐朽程度真值[16-19]。本研究结合立木损伤目测法,将立木腐朽等级作为因变量。以质量损失率将立木腐朽程度划分为5个等级作为真值,等级越高则腐朽程度越严重。木芯质量损失率在15%以下,为Ⅰ级;大于或等于15%,小于20%,为Ⅱ级;大于或等于20%,小于30%,为Ⅲ级;大于或等于30%,小于35%,为Ⅳ级;大于或等于35%,为Ⅴ级,其数据来源实验室前期数据。为直观了解样本数据处理情况,表1统计分析各数据的平均值、标准差、最大值、最小值。

表1 样本数据处理结果统计
由于红松活立木数据在野外获取比较困难,获取的样本量较少及无法保证各腐朽等级之间的数量一致,为充分利用采集的30组数据(腐朽等级Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ的数量分别为7、6、4、3、10组),保证样本数据在训练及测试时各等级分类均衡,采用重复分层K折交叉验证将数据集划分为训练集和测试集(2/3为训练集,1/3为测试集)用来测试模型的泛化性能,其中重复分层K折交叉验证法的折叠数为3,重复次数为5次。
2.2 模型介绍
Breiman[20]在2001年提出随机森林(RF)。随机森林是在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入随机属性选择。随机森林是通过在训练时构造大量具有随机选择特征的决策树,然后在不同的观测样本上训练每棵决策树,并根据每个决策树的预测结果,选择分类投票数最大概率值所对应的类别作为最终预测结果[21]。
逻辑回归是因变量为二分类或多分类时,观察结果与影响因素之间关系的一种多变量分析方法,属概率型非线性回归[22];支持向量机是运用统计学习理论的机器学习方法,使用训练数据在样本空间或特征空间里寻找最大间隔分离超平面或合适的核函数,然后将不同样本类别分开[23];决策树是一种监督学习方法,利用树形结构,根据分类规则进行逐层决策,将样本类别进行分类[9]。
随机森林通过Python软件和sklearn-0.23.1中的RFC实现,支持向量机、决策树分别使用sklearn-0.23.1中的SVC、Decision Tree Classifier[24],逻辑回归使用了logistic回归模型。
2.3 模型性能评价
在分类问题求解过程中,多为二分类问题,常用的评估指标有准确率、精确率、召回率、F分数等[25],然而精确率和召回率只能衡量分类器对单个类别的局部分类性能,不满足本研究多分类的情况。因此,本研究采用微观和宏观平均下的各项评估指标来评价全局分类性能。此外,由于各腐朽程度级别的样例数不均衡,于是引用了权重平均值来衡量分类结果。在评价的过程中不能单纯看分类结果,还需对分类器的优劣进行评价。其公式见表2。
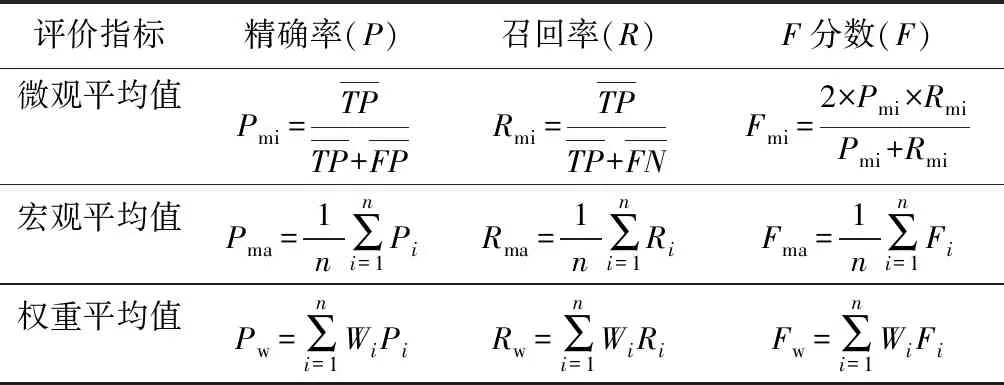
表2 各评价指标公式
分类器的优劣主要通过接受者操作特性曲线(ROC曲线)进行评价。ROC曲线经常以图表的形式展示一项试验或一系列试验的每一个合理临界值的真阳性率和假阳性率之间的关联或权衡,其中曲线图以真阳性率(RTP=TPi/(TPi+FNi))为纵坐标,假阳性率(RFP=FPi/(TNi+FPi))为横坐标绘制[26]。在ROC曲线中,越靠近左上角,分类准确性越高;越接近空间45度对角线,分类精度越低[27-28]。AUC是ROC曲线下方的面积,也是衡量学习分类器优劣的一项性能指标,对应的AUC值越大表示分类器效果更好。多类ROC曲线分析分为宏观平均ROC曲线和微观平均ROC曲线2种类型。宏观平均ROC曲线自由测量每个类别的度量,取平均值;微观平均ROC曲线聚集所有类别来参与计算,取平均度量[29]。虽然在多分类设置中,微观平均是有利的,但在本研究中,我们同时考虑了两者。
3 结果与分析
3.1 随机森林模型构建
随机森林分级模型以心材异常面积比、边材异常面积比、阻力损失为输入量,腐朽等级为输出量,利用训练集来训练模型,再通过测试集测试模型的泛化性能,最后通过随机森林分析变量因子对因变量影响的相对重要性。在RFC中,主要调节的参数为N估计,其他参数为默认值。N估计指的是随机森林中的树木数量,数量的多少会影响模型的准确性,于是通过学习曲线方法得出最佳N估计值。由图1可知,当N估计值为16时的学习得分高于默认值,为10。
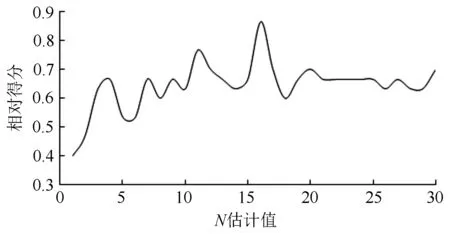
图1 N估计的学习曲线
3.2 变量因子的相对重要性
通过随机森林对训练样本进行拟合,计算每个变量特征的平均不纯度(基尼系数)减量,得出各变量因子的重要性。其中,对立木腐朽程度分级影响最大的是心材异常面积比,占比为0.355;其次是阻力损失,占比为0.335;最后是边材异常面积比,占比为0.310。
3.3 随机森林模型结果的检验
根据训练数据构建的随机森林分级结果与真实腐朽等级的热力图混淆矩阵(图2)。20组训练数据中均无腐朽等级数据辨识错误,其训练精度为100%,总体的误判率为0%。为了进一步验证模型的泛化能力,将测试数据输入到随机森林模型中,输出的结果如图3所示,10组测试数据中有1组预测错误,真实腐朽等级Ⅲ被判为腐朽等级Ⅱ,其他预测的腐朽等级与真实腐朽等级相同。因此,模型的泛化精度为90%,说明随机森林学习模型对未知数据的辨识能力较强。
进一步分析随机森林在总体数据上的拟合,从表3可知,腐朽等级Ⅱ的精确率为85.71%,召回率为100%;腐朽等级Ⅲ的精确率为100%,召回率为75%,说明真实腐朽等级Ⅲ的数量没有真正全部预测正确,有1组腐朽等级Ⅲ误判为腐朽等级Ⅱ,因此腐朽等级Ⅱ的数目多1组,所以腐朽等级Ⅲ的召回率为75%,腐朽等级Ⅱ的精确率为85.71%。由召回率可以看出4个真实腐朽等级(腐朽等级Ⅰ、Ⅱ、Ⅳ、Ⅴ)都被准确辨识,均无判错。腐朽等级误判的原因如下:首先,当质量损失率为15%~30%时,在腐朽菌的作用下,其力学性能和化学成分仍在发生持续、复杂的变化,各项性质较不稳定[6];第二,Ⅲ级、Ⅱ级腐朽的立木即使属于同级别,各项指标数值也可能存在较大差异,所以难以预测真实的腐朽程度;第三,由于立木内部的部分缺陷,无损检测设备没有识别出来;最后,由于各样本腐朽等级数目不平衡及总的样本数量有限,不足以完整训练各个腐朽等级区间的特征,因此腐朽等级Ⅲ被误判为腐朽等级Ⅱ。从表4中还可知,随机森林模型的整体分类的微观平均值精确率、微观平均值召回率以及相应的微观平均值F分数分别为0.966 7,0.966 7,0.966 7;宏观平均值精确率、宏观平均值召回率以及相应的宏观平均值F分数分别为0.971 4,0.950 0,0.956 0;权重平均值精确率、权重平均值召回率以及权重平均值F分数分别为0.971 4,0.966 7,0.965 6。以上指标反映,运用随机森林的活立木腐朽分级模型具有较强的辨识能力,可以准确判别腐朽等级。
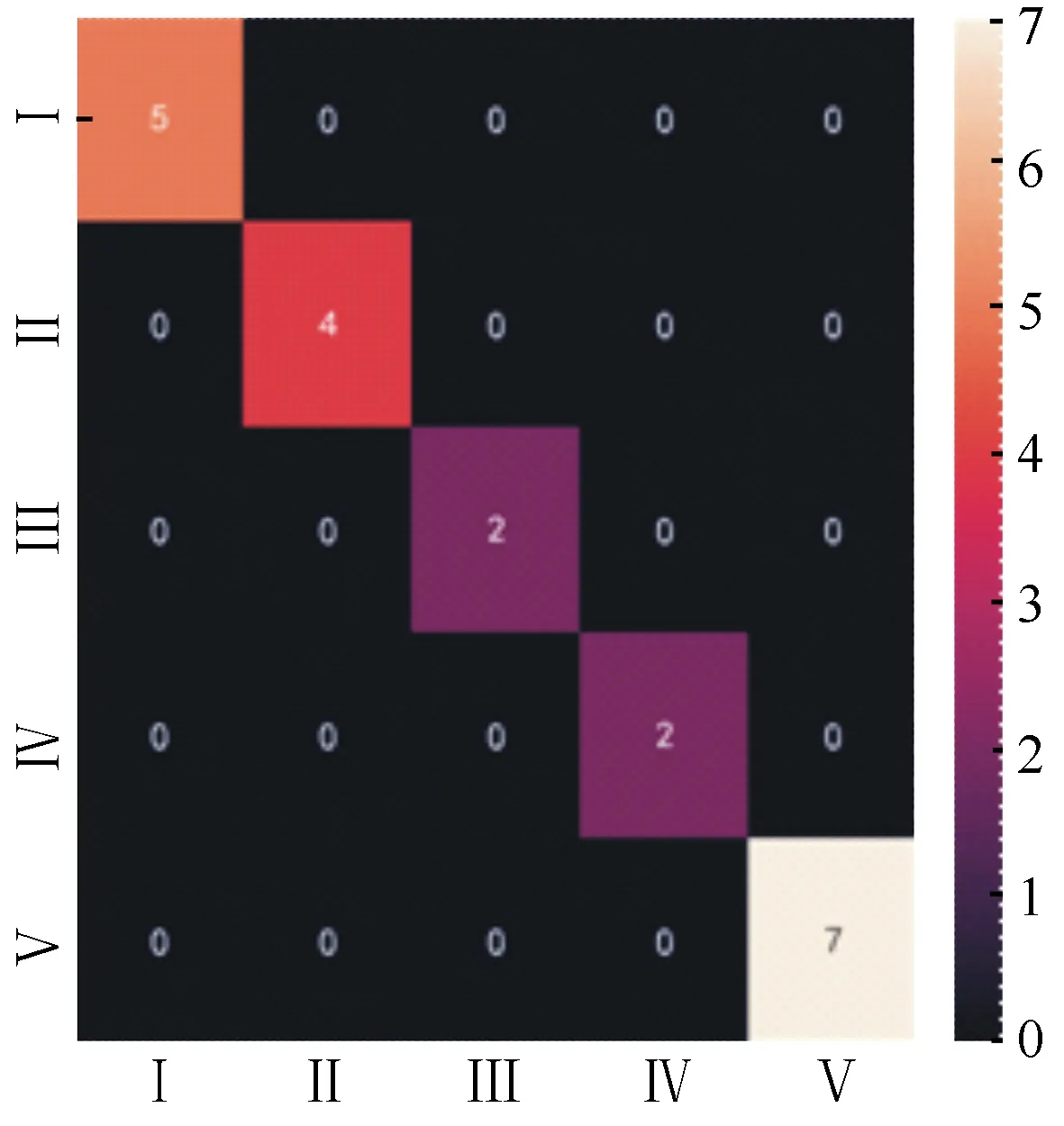
图2 训练集腐朽等级热力图混淆矩阵
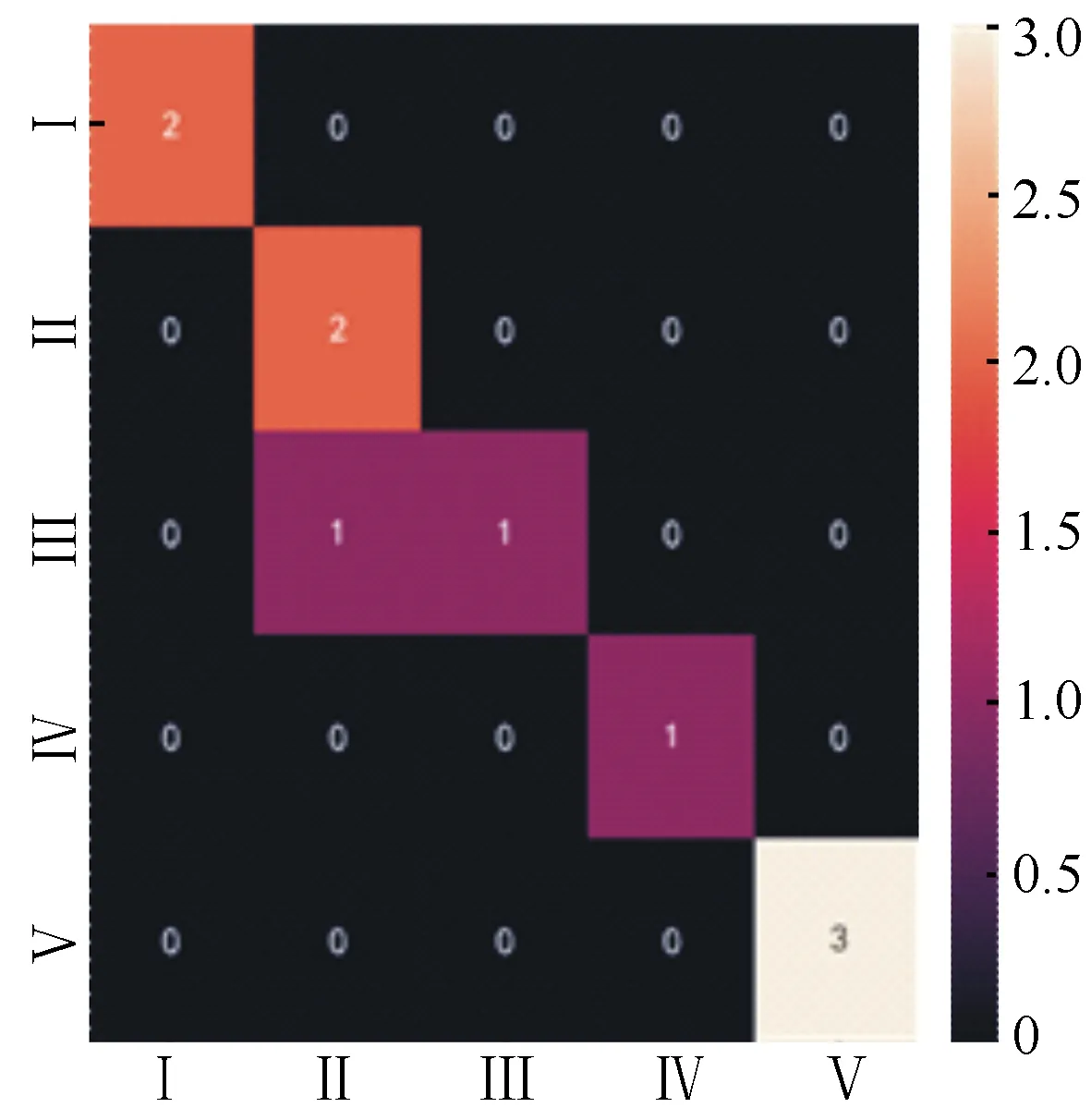
图3 测试集腐朽等级热力图混淆矩阵
3.4 不同分级模型比较
使用模型性能评价指标,分别比较宏观平均值、微观平均值、权重平均值下的F分数,精准率、召回率3个指标及宏观、微观平均值下的AUC指标,用于衡量不同分级模型的性能和效果。表5是随机森林,决策树、支持向量机、逻辑回归的基准分类器在各评估指标上的性能评估。
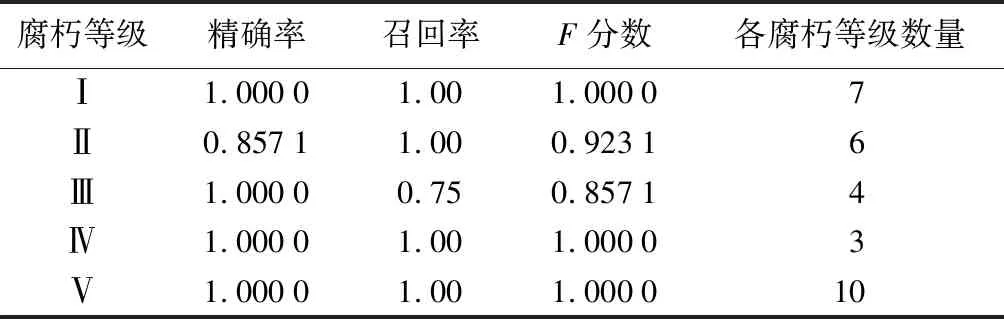
表3 立木各腐朽等级评价

表4 立木腐朽分级总数结果评价
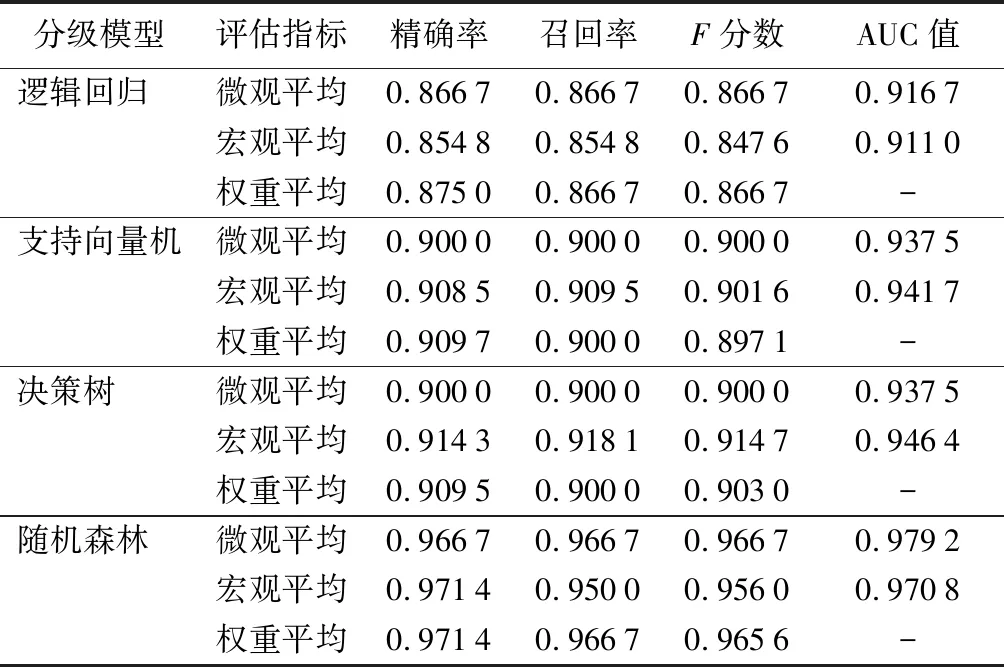
表5 不同分级模型的评价
在4个分级模型中,微观平均值精确率、微观平均值召回率、微观平均值F分数的评估指标由大到小排列均为随机森林、支持向量机及决策树、逻辑回归;宏观平均值精确率、宏观平均值召回率、宏观平均值F分数评估指标由大到小排列均为随机森林、决策树、支持向量机、逻辑回归。其中从表3可以看出,各腐朽等级数量不平衡,总数量为30,5个腐朽等级平均数量为6,腐朽等级Ⅳ的数量为3,与平均数量相差50%,腐朽等级Ⅴ的数量为10,与平均数量相比高出66.7%。对于不平衡的数据使用权重平均值精确率、权重平均值召回率、权重平均值F分数来评估,权重平均值精确率由大到小依次为随机森林、支持向量机、决策树、逻辑回归;权重平均值召回率由大到小依次为随机森林、支持向量机及决策树、逻辑回归;权重平均值F分数由大到小依次为随机森林、决策树、支持向量机、逻辑回归。通过各评价指标可以看出,随机森林优于其他3种分级模型。支持向量机、决策树在宏观平均值和权重平均值上各占优势,两者之间差距甚小,尚无法对两者进行比较。所以,可以通过ROC曲线图及其曲线下方的面积AUC对各模型在全局准确性和分级效果方面进行评价。
通过对4种分级模型下微观、宏观平均ROC曲线(图4,图5)比较可知,随机森林模型的微观、宏观平均ROC曲线最靠近左上角,其次是决策树、支持向量机的微观平均ROC曲线,最后是逻辑回归模型的微观平均ROC曲线。由此说明,随机森林模型的整体测试准确性最好。对于活立木腐朽程度的分级效果,AUC值越大,其分级效果越好。微观平均AUC值由大到小依次为随机森林(0.979 2)、支持向量机及决策树(0.937 5)、逻辑回归(0.916 7),说明在活立木腐朽分级方面,决策树、支持向量机的分级效果比逻辑回归好,但相较于随机森林略有不足。决策树、支持向量机的微观平均ROC曲线重合且AUC值相等,因此不好判别两者之间分级性能的高低,这时需要参考其他性能度量(宏观平均ROC曲线、AUC)来评价。
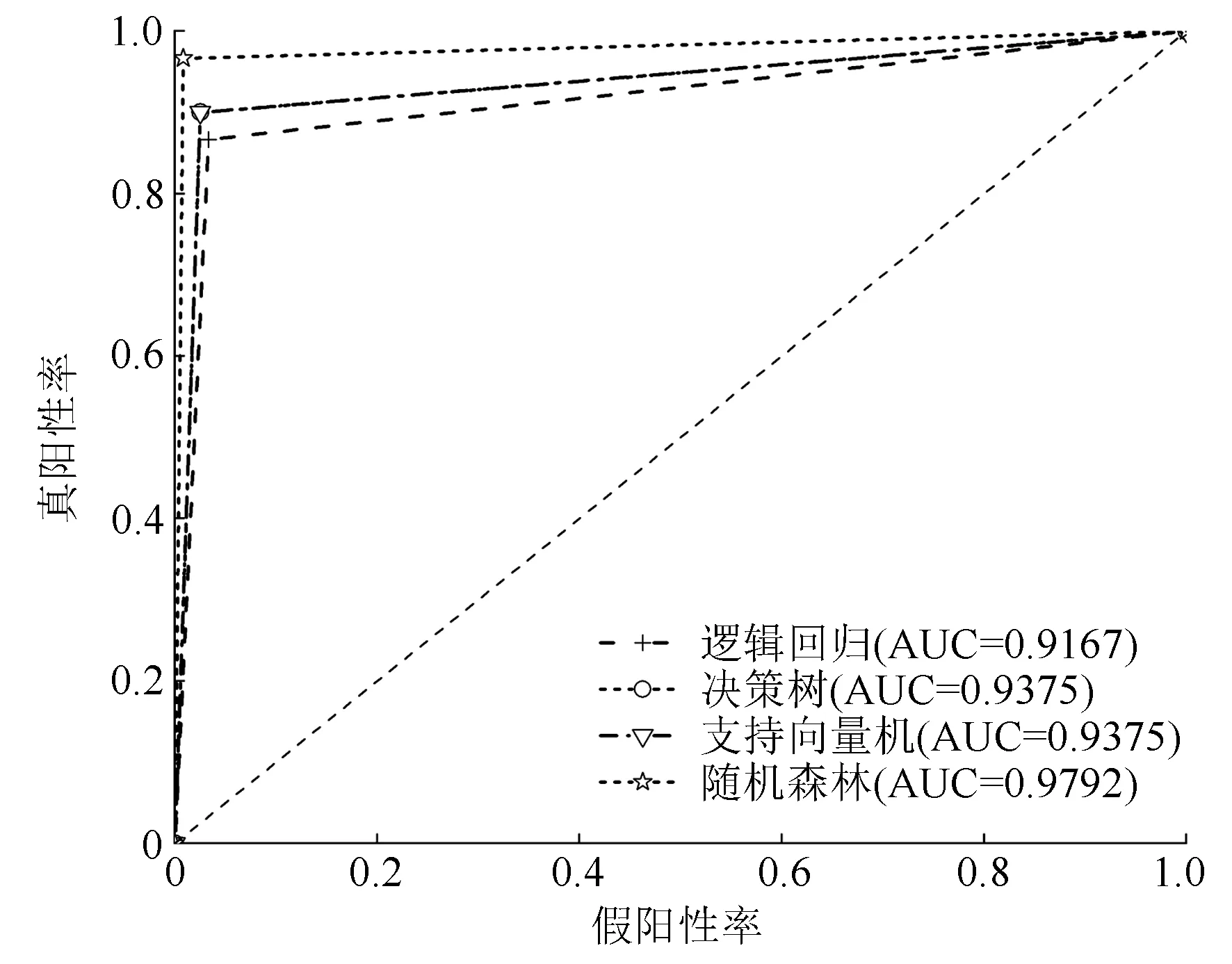
图4 微观平均ROC曲线及其AUC值
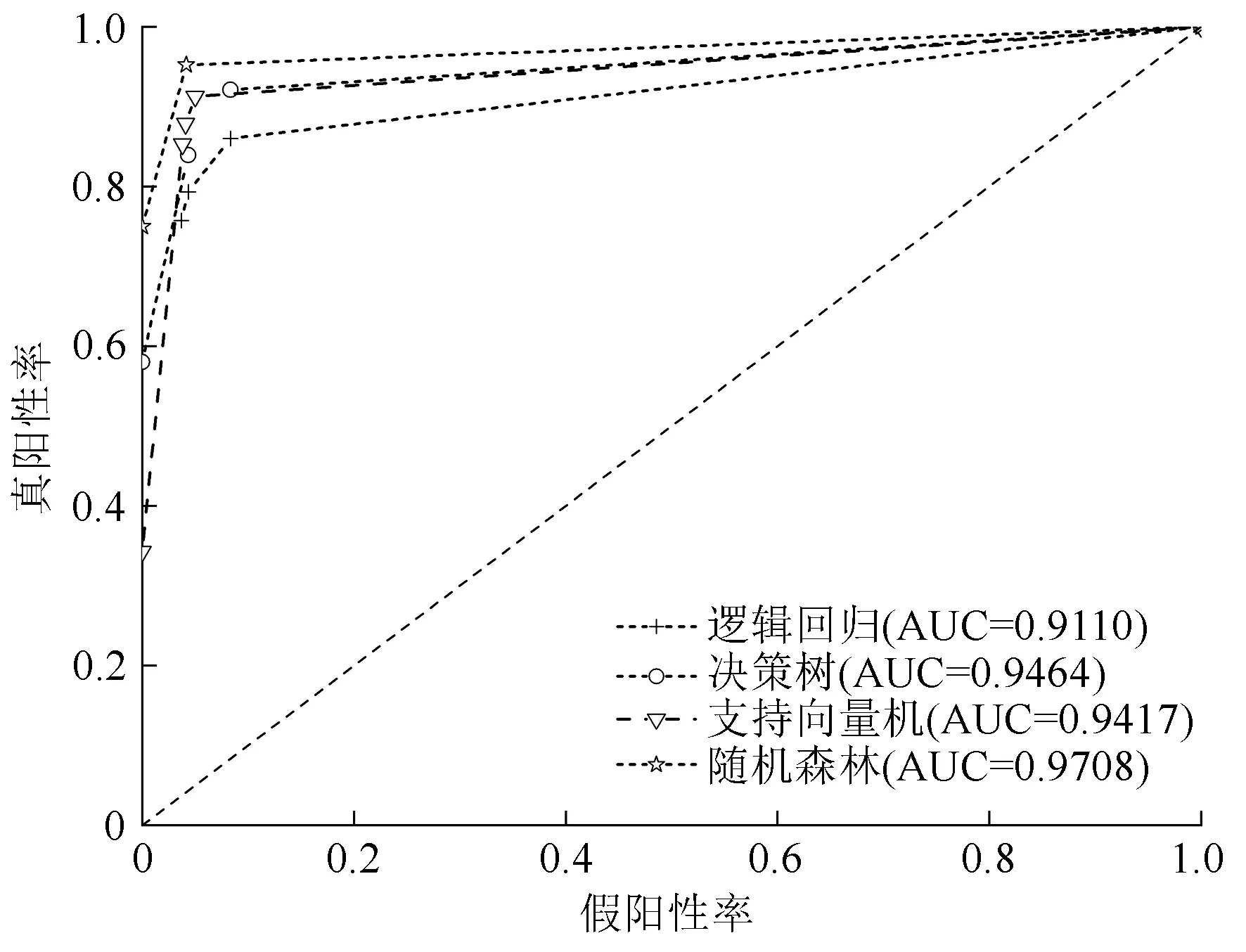
图5 宏观平均ROC曲线及其AUC值
由图5中4种分级模型的宏观平均ROC曲线可以计算出曲线下的AUC值,其中随机森林,决策树、支持向量机、逻辑回归模型的宏观平均AUC值分别为0.970 8,0.946 4,0.941 7,0.911 0。决策树、支持向量机的宏观平均AUC值相差较小,决策树的分级效果比支持向量机稍好;随机森林的宏观平均AUC值比另外3种模型都高,说明随机森林模型的分级效果更好。综上所述,运用随机森林的立木腐朽分级模型较其它3种模型而言,整体测试准确性及分级效果更好。
4 结论
本研究运用随机森林模型对五营森林公园中的不同腐朽程度红松进行分级,选取无损,易获取指标(阻力损失及心材、边材异常面积比)为模型自变量,以木芯质量损失率划分各腐朽等级区间,并使用重复分层K折交叉验证保证样本数据在训练及测试时分类均衡。经过训练及测试,随机森林的训练精度为100%,测试精度为90%,说明随机森林模型对立木腐朽分级表现出稳健的拟合能力和较强的泛化能力。使用随机森林模型对立木腐朽等级进行分级,腐朽等级(Ⅰ、Ⅱ、Ⅳ、Ⅴ)的召回率都为100%,说明各腐朽等级都被正确辨识,只有腐朽等级Ⅲ被错判1例。本研究全部数据在随机森林模型进行拟合,全局腐朽分级准确率高达96.67%,宏观、微观、权重平均F分数分别为0.956 0、0.966 7、0.965 6,宏观、微观平均AUC值分别为0.970 8、0.979 2,说明随机森林活立木腐朽分级模型具有较强的辨识能力,可以准确判别各腐朽等级,并优于其他3种模型。本研究只是将随机森林应用到红松腐朽分级评估,但该方法也适用于其他树种。因此,本研究对经营好森林,减轻灾害损失,提高经济效益有着重要意义。

