基于SVD与小波变换的反高频脉冲磁场窃电方法

阙华坤，林国龙，曹云飞，冯小峰，江泽涛，李 健，范竞敏

（1. 广东电网有限责任公司 计量中心，广州 518049；2. 广东工业大学 自动化学院，广州 510006）

0 引言

随着电网智能化的推进，窃电技术层出不穷［1］。近几年不少不法分子利用高科技设备产生高频脉冲磁场影响电能表中央处理器，使得电能表不能正常计数［2］。针对此类窃电方法，研究人员提出了加装防窃电装置直接对高频脉冲电磁信号进行实时检测的方法［3—4］，实现系统的自动运行，不仅可以判断出用电异常情况，而且能够准确及时地判别出窃电行为，为防窃电工作带来了便利。但是高频脉冲磁场信号往往混杂在各种噪声中，噪声会干扰防窃电装置的判别，使防窃电装置失效，为检测增加了难度。针对此问题，本文提出利用SVD 和小波变换相结合的方法将高频脉冲磁场信号从噪声中分离出来，从而提升防窃电装置的识别准确率。

在噪声抑制方面现常见的处理方法有EMD法［5］、小波降噪法［6］、FFT 阈值法［7］和SVD 法以及各种改进版方法。本文在前人的研究基础上，提出一种SVD 结合小波变换的方法。首先利用FFT 功率谱确定高频脉冲磁场信号的数量，用于确定有效秩阶次；其次利用SVD分解并将噪声对应的奇异值置零之后重构信号，进而抑制噪声［8］。单纯使用SVD算法可以消去窄带噪声，但不能很好地消去随机噪声，故再对去噪信号进行小波变换去除随机噪声。仿真和实验结果表明本文方法优于FFT 阈值法和EMD法，可以更大程度地去除噪声并保留高频脉冲窃电信号。

1 方法原理

1.1 SVD去窄带噪声算法原理

SVD 法是一种在信号处理中广泛运用的算法，在降噪方面有较好的零相移特性和稳定性［9］，主要分为3个步骤。首先利用相空间理论对染噪信号构建矩阵，确定有效秩阶次，最后将噪声的奇异值重构以分离出有用信号。

（1）将染噪信号y(t)进行矩阵构建，通常选用Henkle矩阵，形式为

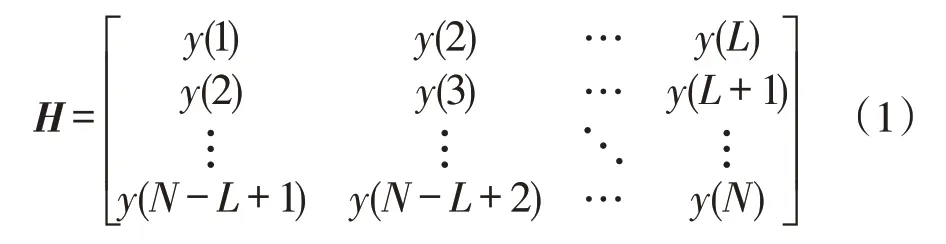
式中：N为染噪信号数据个数；L为窗长度，研究发现矩阵行数为信号长度一半时有较好的去噪效果［10］，一般当N为偶数时，L取N/2，当N为奇数时，L取（N-1）/2。本文L取为N/2。

（2）对H矩阵进行奇异值分解

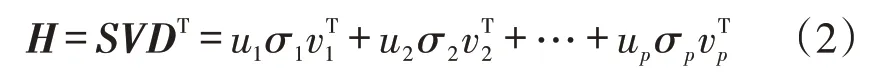
式中：S为HHT的左奇异矩阵；D为HTH的右奇异矩阵；V为奇异值对角矩阵，V=diag(λ1,λ2,…,λk,…,λp)，其中λk为H矩阵的奇异值，按降序排序，p=min(L,N-L+1)；u、σ、v分别为S、D、V中的元素。由式（2）知H矩阵可分解为多个奇异值及奇异矢量矩阵的线性叠加。

（3）奇异值处理及重构信号

λk在数值上与信号一一对应，高频脉冲窃电信号对应较小的λk，窄带噪声信号对应较大的λk，通常根据λk数值的突变或λk数值的聚类分布来划分信号的奇异值，本文利用窄带噪声的数量n来划分。文献［11］证明了每个频率的窄带噪声信号都与两个较大的非0 奇异值相对应，同时窄带噪声数量对应频谱超过阈值的数量，利用频谱确定n，将前2n个奇异值置零后进行信号重构。设将对应奇异值处理后得到的新对角阵为V′，重构后的Henkle矩阵为H′，表示为

对于重构后的矩阵H′进行反对角平均［12］，从而抑制窄带噪声。

1.2 小波变换去随机噪声原理

小波变换去噪多用于局部特征的处理，其基本原理是通过小波变换将染噪信号分解成多个尺度，由此把有用部分和无用部分分隔开，噪声信号的能量集中在幅值较小的系数上，有用信号则集中在较大的系数上。根据这个原理，选取适合的阈值和阈值函数将各个尺度的噪声信号去除，最后进行小波逆变换得到重构的去噪信号［13］。去噪处理的具体步骤如图1所示。

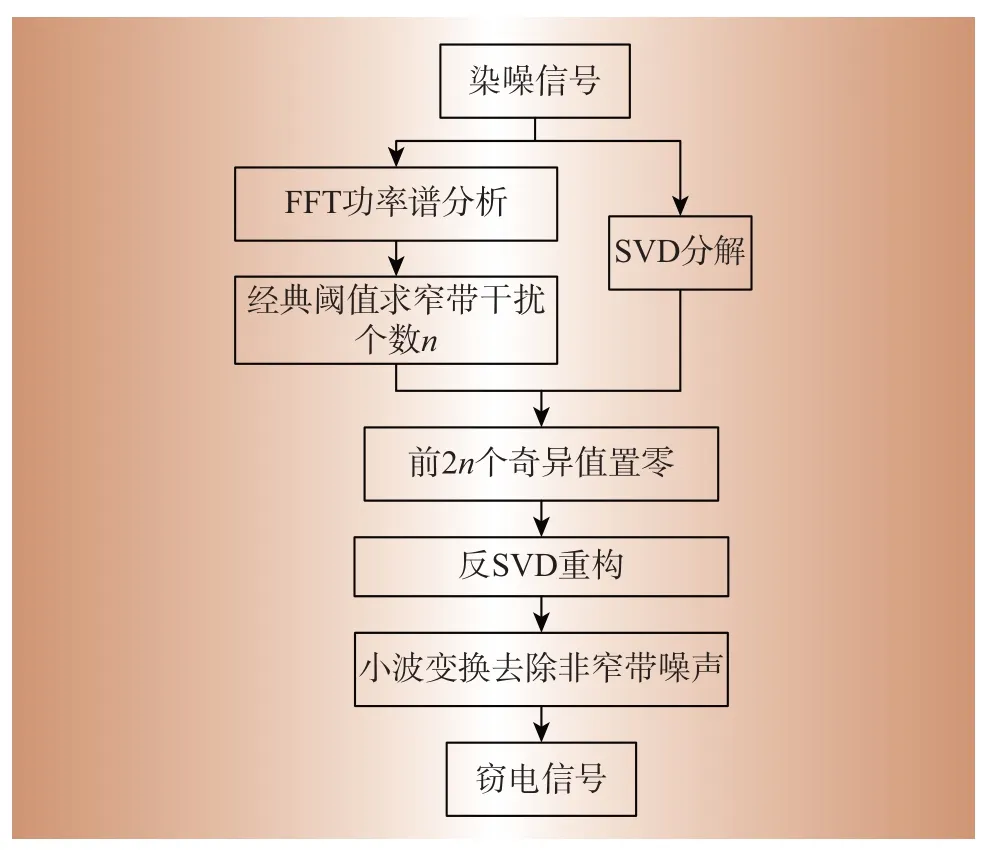
图1 算法流程Fig.1 Algorithm flow

2 高频脉冲磁场信号仿真去噪分析

2.1 信号仿真

为了方便分析，文中采用仿真信号对高频脉冲磁场信号和噪声信号进行研究。高频窃电信号符合高频指数衰减模型，文中采用4 种形式对高频脉冲磁场信号进行模拟，具体如下。

单指数衰减形式，表达式为

单指数衰减震荡形式，表达式为

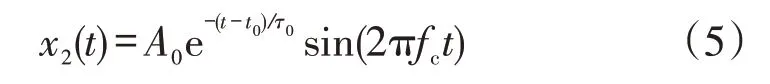
双指数衰减形式，表达式为

双指数衰减震荡形式，表达式为

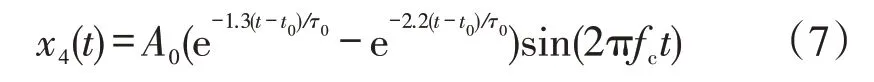
式中：A0为幅值，分别取0.4 mV、0.4 mV、0.3 mV、0.3 mV；t0为电能表信号检测时间，分别取35 ms、5 ms、25 ms、15 ms；τ0为衰减系数，取0.1 ms；fc为震荡频率，取20 kHz。采样频率设置为1 MHz，时间窗口设为40 ms。高频脉冲窃电信号如图2（a）所示。

考虑到随机噪声，引入6 dB的高斯白噪声。在这基础上再叠加6个频率不同的窄带噪声来模拟噪声环境，如式（8）

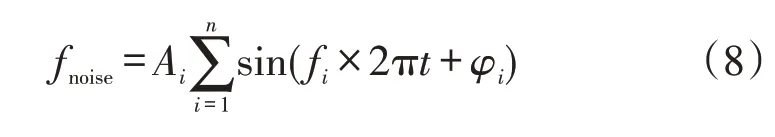
式中：Ai为噪声干扰幅值，分别取0.10 mV、0.15 mV、0.11 mV、0.21 mV、0.18 mV、0.17 mV；fi为噪声干扰频率，分别取0.92 kHz、1.31 kHz、2.01 kHz、2.60 kHz、3.40 kHz、7.00 kHz；φi为噪声干扰初始相位，分别取30°、-45°、45°、-30°、0°、-60°。噪声干扰的时域波形如图2（b）所示。

将高频脉冲窃电信号和噪声信号叠加得到染噪信号y(t),其波形如图2（c）所示。

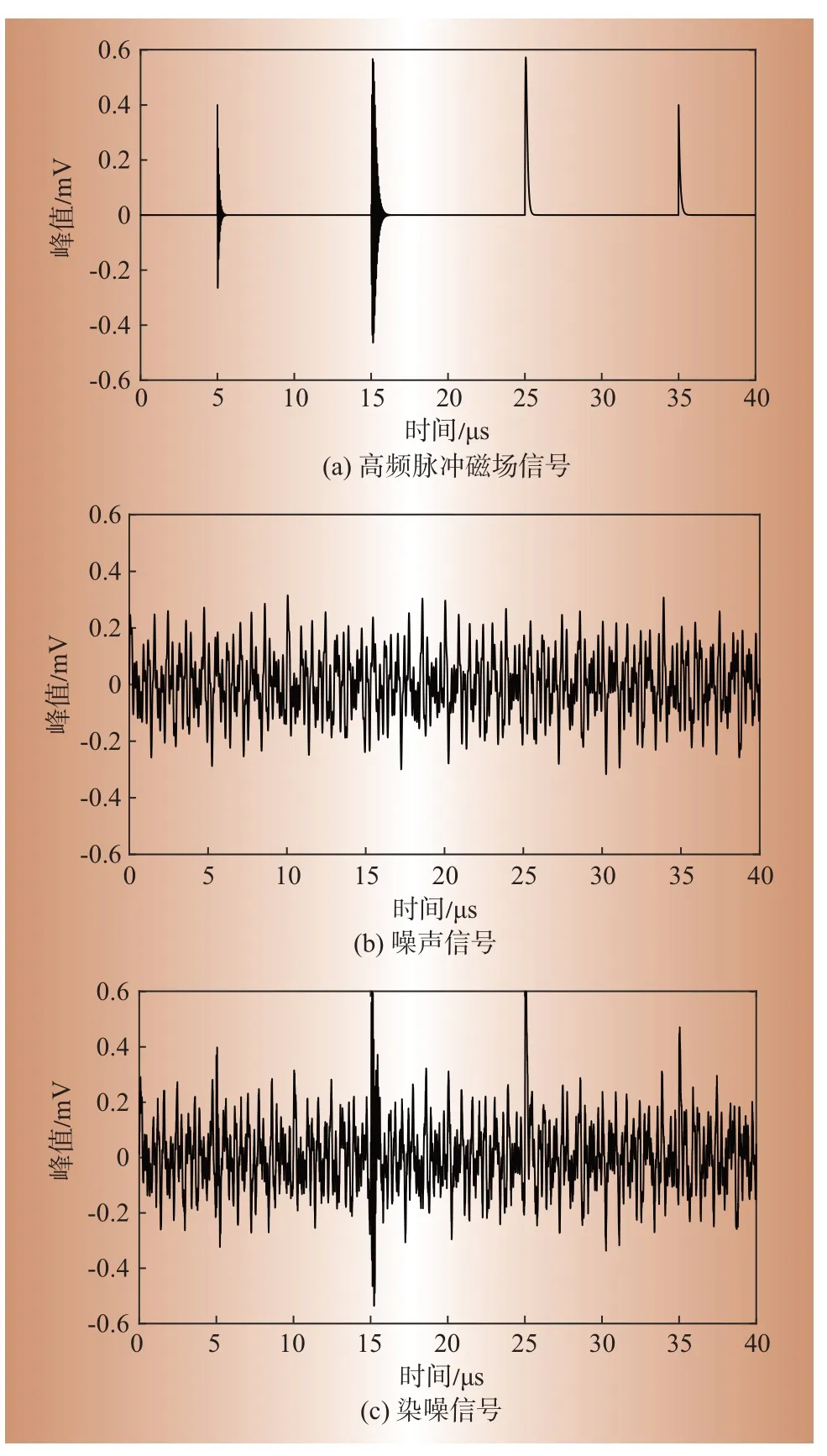
图2 仿真脉冲磁场信号Fig.2 Simulated pulsed megnatic field signal

2.2 功率谱分析

设信号f(t)的FFT变换为F(ω)，表达式为

其功率谱为

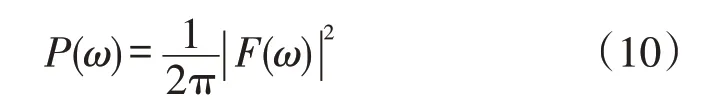
染噪信号对应的FFT功率谱如图3所示。当出现噪声干扰后，信号的功率谱在各噪声频率处有很强的干扰尖峰，而高频脉冲窃电信号功率谱脉冲相比噪声干扰信号功率谱脉冲小得多，因此引入经典阈值，表示为

图3 FFT功率谱Fig.3 FFT power spectrum

式中：T为设定的阈值；σ为数据的标准差；N为数据的个数。尖峰比经典阈值高的即为噪声干扰信号，从而确定染噪信号中的窄带噪声个数。

利用阈值T在FFT功率谱中自适应确定高频脉冲磁场的数量，并以此作为奇异值重构分配依据，解决SVD难以确定有效秩阶次的问题。

2.3 去噪效果对比

对图2（c）的染噪信号按本文方法进行SVD 处理，由FFT功率谱可得窄带噪声的数量为6个。图4为SVD分解后前30个奇异值，可看出需置零的奇异值为前12个，即每2个奇异值对应一个窄带干扰噪声，奇异值置零重构信号后得图5（a）所示去噪结果，可以看出仍有部分随机噪声没有被剔除。再如前文所述对其进行小波变换处理，为了更准确地检测出窃电信号，选择正则性更好的Daubechies 系列小波基函数使重构信号更光滑。根据实测数据实验比对，选取‘db2’小波基函数、硬阈值函数，分解层数为6层，去噪结果如图5（b）所示。利用FFT阈值法和EMD 法处理染噪信号分别得到图5（c）和图5（d）。对比可知,应用小波变换后SVD 法的去噪效果进一步提升，同时很好地保留了有用信息，能较好地提取出高频脉冲窃电信号，而FFT 阈值法保留有较大的噪声，不利于高频脉冲窃电信号的检测识别，EMD法噪声残留比FFT阈值法和SVD法相对较小，但出现高频脉冲磁场峰值削减，有较大的波形失真现象，这会使得反窃电装置不动作，所以本文方法去噪效果更佳。

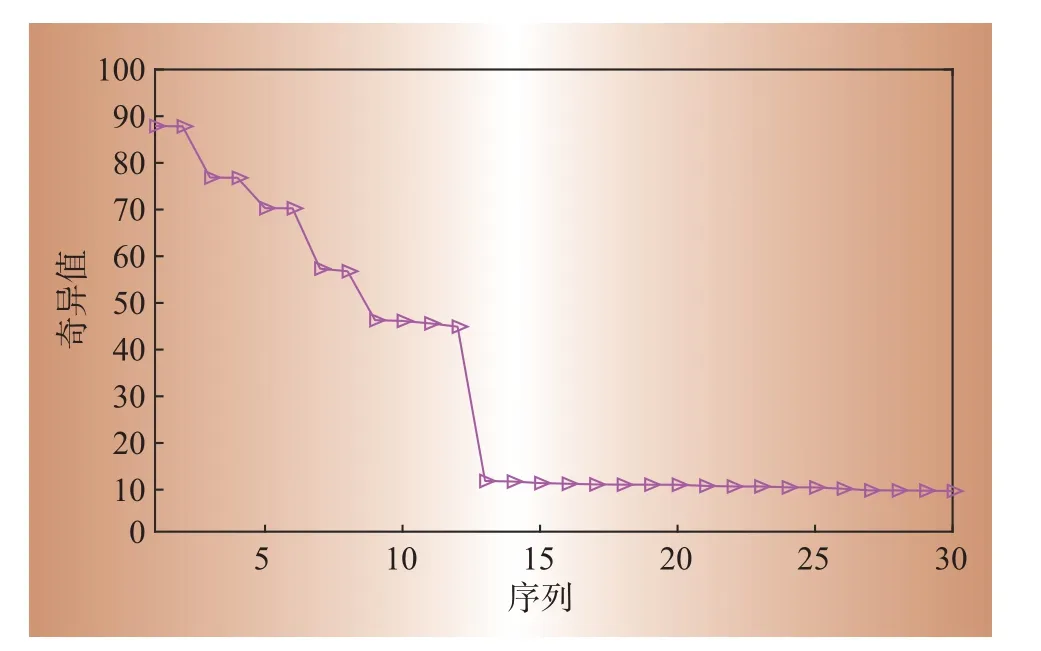
图4 信号奇异值Fig.4 Singular values of signal

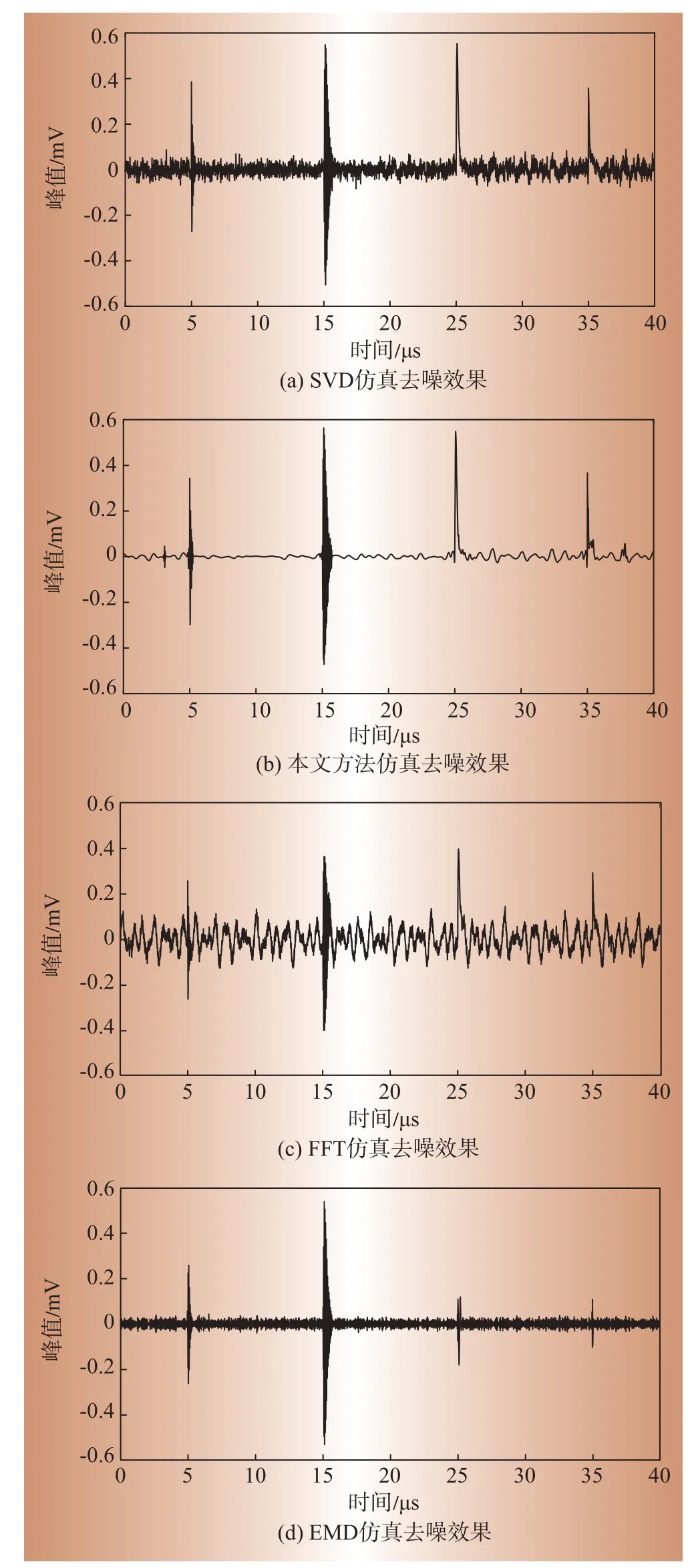
图5 仿真去噪效果对比Fig.5 Comparison of the results after suppressing the noise

为了定量描述本文方法、FFT阈值法和EMD法3种方法的去噪效果，引入噪声抑制比、均方误差、波形相关系数和平滑度4个评价指标分别如式（12）—式（15）所示。具体形式为

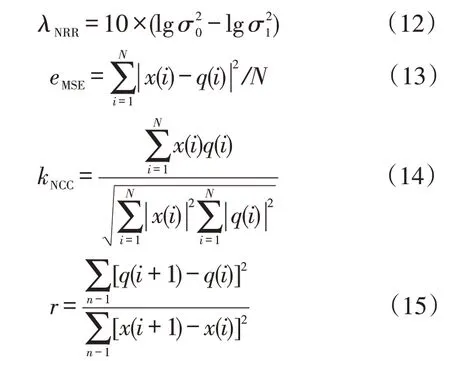
式中：σ0、σ1分别为去噪前、后的信号方差；x(i)为干净信号；q(i)为去噪后信号。

噪声抑制比越大，说明信号中的噪声越小；均方误差越小，波形相关系数越接近1，说明与干净信号越接近，去噪效果越好，平滑度越小越平滑。

4 个指标计算结果如表1 所示，结果表明，FFT阈值法的噪声抑制比相比于其余方法小得多，去噪效果不佳；EMD 法虽然噪声抑制比最大，但均方误差很大，波形相关系数也不高，波形失真，效果并不好；而SVD 算法相比于FFT 阈值法的信噪比更高，均方误差更小，波形相关系数也更接近1；本文方法较SVD法的4个指标性能都明显提升。整体上本文方法抑制噪声的效果更好，更有利于防窃电装置的检测。

表1 去噪效果对比Table 1 Comparison of the results after suppressing thenoise

3 实验验证

为验证改进去噪算法对实测信号的效果,本文在实验室搭建系统，如图6所示，利用信号调理板发出信号控制电磁铁产生特定的脉冲电磁场，采用磁场传感器将电磁场转换为一定频率的高频脉冲磁场信号，将在噪声环境下的高频脉冲磁场信号输入信号采集板进行采集，并在串口屏显示。实验测量信号如图7所示。

图6 实验系统Fig.6 Measurement system

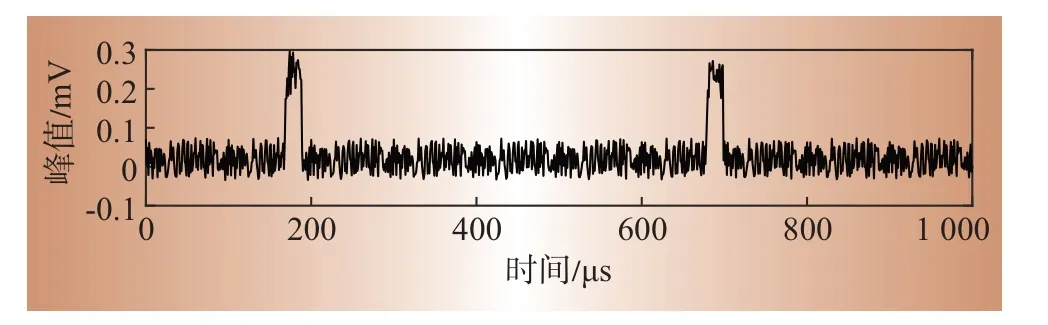
图7 实测信号Fig.7 Measurement signals

为了检验本文提出的去噪方法对实测窃电信号的有效性和适用性，按照前文方法对实测信号进行去噪处理。

FFT 频谱如图8 所示，由频谱阈值确定噪声中窄带噪声数量为1。将前2个奇异值置零重构后，选取分解层数为6 层，使用硬阈值函数、‘db2’小波基函数对其进行小波分解。本文算法去噪后信号如图9（a）所示。作为比较，同时采用FFT 阈值法和EMD分解法对实测信号进行去噪，去噪后信号如图9（b）和图9（c）所示。

图8 实测信号FFT功率谱Fig.8 FFT power spectrum of measurement signals

结果显示实测结果与仿真结果相匹配。由图9 可知，FFT 阈值法由于频谱泄漏的问题保留有较大的噪声和较明显的边缘效应，且存在毛刺，去噪效果不够明显，影响窃电信号的识别；EMD 分解法拾取了信号特征相对丰富的频带，但由于频谱混叠的问题出现了一定的波形失真现象，没有完好地分解出高频脉冲窃电信号；本文方法在平滑滤波的同时较两种方法能更大程度地保留有用信息，提高噪声抑制比，在微弱噪声的处理上有凸出优势，能较好地消除噪声并提取出高频脉冲窃电信号。

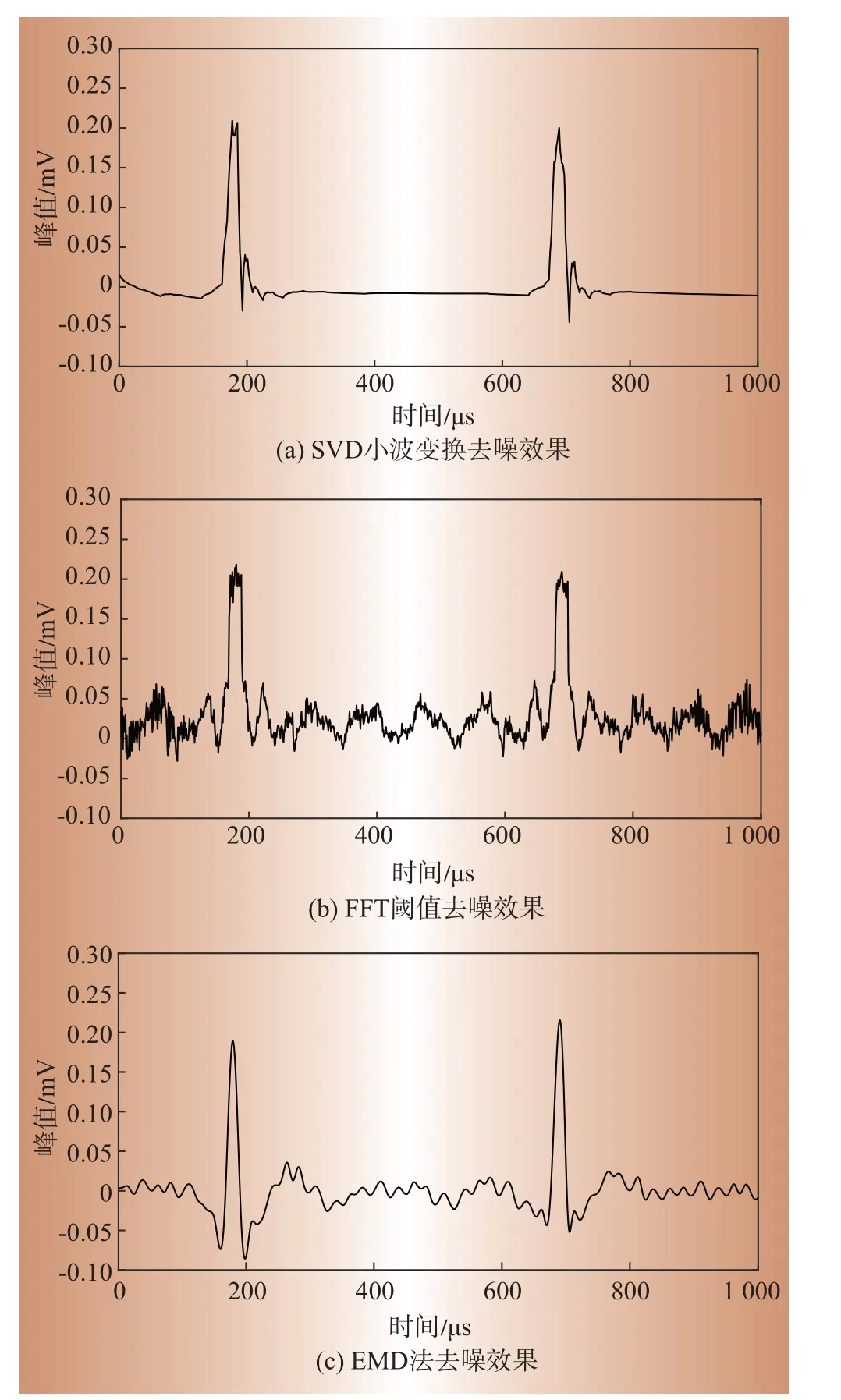
图9 实测去噪结果对比Fig.9 Comparison of the measurement results after suppressing the noise

4 结束语

本文分析了高频脉冲磁场混合噪声的FFT功率谱，结合经典阈值确定窄带噪声数量，并以此确定需要置零的奇异值，解决了SVD难以确定有效秩阶次的问题。通过使用SVD 算法和小波变换结合的方法进行去噪处理，解决了传统SVD对随机噪声去噪效果较差的问题，仿真结果表明该方法对含有随机噪声和窄带噪声的窃电信号有较好的效果，且对比发现效果优于FFT阈值法和EMD法。

但研究表明，本文方法尚有不足，去噪后存在信号小部分波形失真的现象。此外实际不同场景中高频脉冲窃电信号和噪声存在差异性，去噪效果也有一定差别，故如何提升去噪算法的准确性和普适性还需要进一步研究。