基于变化趋势和气象因子的加权负荷预测方法

谭风雷，丁心志，张 军，陈 昊，何嘉弘

（1. 国网江苏省电力有限公司 超高压分公司，南京 211102；2. 云南电力试验研究院（集团）有限公司，昆明 650217；3. 东南大学 电气工程学院，南京 210096）

0 引言

随着社会经济快速发展，人们生活质量迅速提高，社会用电量逐年增加，但由于电力负荷的随机性和波动性，使得电力负荷变化较大，需要提前预测电力负荷并制定电能生产曲线［1—3］。

电力负荷的预测方法已有很多，主要包括回归分析法、时间序列法、负荷求导法、指数平滑法、神经网络、支持向量机、模糊理论等［4—6］。文献［7］考虑负荷趋势变化，提出了基于变化趋势的电力负荷预测方法，并通过算例验证了算法的有效性。文献［8］基于环境因素，提出了一种改进的指数平滑法，具有简单、预测精度高的优点。文献［9］基于温度对电力负荷的影响，提出了多日积温效应和两日积温效应2 种概念，并基于支持向量机对电力负荷进行了预测。总体来讲，电力负荷预测方法主要分为两类：传统预测方法和现代预测方法，传统预测方法是基于数学工具进行计算，算法简单但预测精度不高；而现代预测方法则是基于人工智能算法进行分析，预测精度较高但算法较为复杂。目前，电力负荷预测方法很多都是基于历史电力负荷数据本身，未充分考虑天气情况、政治情况等外界因素。但实际上外界因素对电力负荷有着较大影响，例如天气情况在对电力负荷有影响的因素中占据了一定比例，在夏季表现得尤为明显，因此不能直接忽略，否则会极大影响预测精度。基于上述分析，为进一步提高电力负荷预测精度，需要尽可能多地考虑外界因素。

基于变化趋势的电力负荷预测方法［10］凭借其简单、预测精度较高的特点，得到了相关技术人员的广泛关注，也取得了一系列的成果。但现有的研究中，相关技术人员未考虑外界因素对负荷变化趋势的影响。为解决上述问题，本文提出了一种基于变化趋势和气象因子的加权负荷预测方法，该方法充分考虑气温、湿度和天气类型3个气象因子对负荷变化趋势的影响，通过归一化处理后，建立了考虑气象因子的加权负荷预测模型，并基于最小二乘法的思想，得到了最优参数。最后通过苏北某地区的历史电力负荷数据验证了该方法的有效性与可行性。

1 基于变化趋势的负荷预测方法

基于电力负荷变化的连续性原理，文献［7］对基于变化趋势的电力负荷预测方法进行了充分研究，其模型为

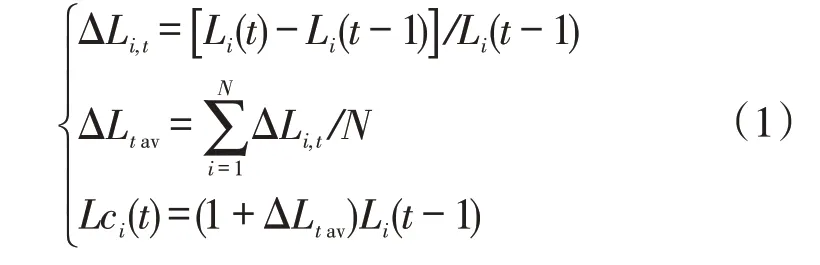
式中：Li(t)为第i天第t时段所对应的实际负荷；ΔLi,t为第i天第t时段的负荷变化率；ΔLtav为第t时段的负荷平均变化率；N为获取的历史负荷数据天数；Lci(t)为基于变化趋势的电力负荷预测方法的预测结果。

分析该模型可知，其存在如下2个问题：

（1）该模型仅仅考虑了电力负荷自身的变化趋势，未考虑外界因素对电力负荷趋势的影响。实际上外界因素对电力负荷具有较大影响［11—12］，如果不予以考虑将会影响预测方法的预测精度。

（2）该模型仅仅考虑了相邻2个时刻的负荷变化率，未考虑任意时刻相对0时刻的负荷变化率，但在实际预测负荷时，往往是已知当日0时刻的电力负荷值，来预测其他时刻的电力负荷，由于该模型只已知相邻2个时刻的负荷变化率，只能通过递推的方法来求解其他任意时刻的电力负荷，这样使得电力负荷的预测结果存在累计误差。设第i天第t时段负荷相对第i天第t-1 时段预测负荷的相对误差为ΔEi(t)，则第i天第t时段实际负荷可以表示为

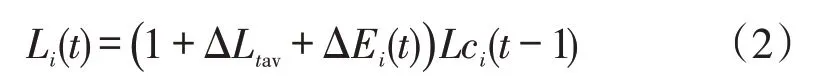
第i天第t时段负荷对应的预测误差Ei(t)为

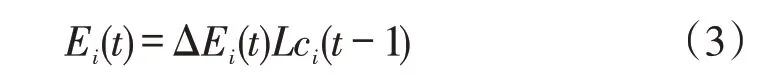
由于第i天第t-1时段负荷为预测值，只能通过第i天第t-2 时段负荷来预测；而第i天第t-2 时段负荷也为预测值，只能通过第i天第t-3 时段负荷来预测；以此类推，需通过第i天第0时段负荷来计算，第i天第t时段负荷为

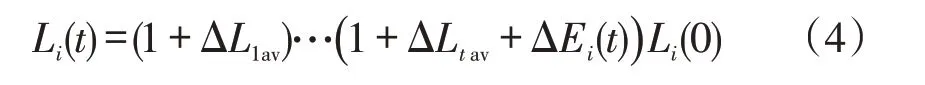
为了简化表达式，设

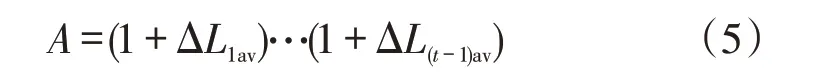
则第i天第t时段负荷对应的预测误差可以表示为

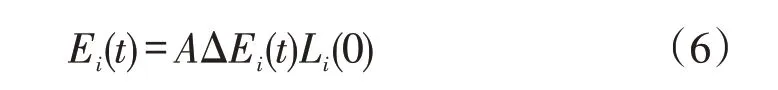
如果可以直接求得第i天任意时段相对第i天第0 时段的负荷平均变化率为；第i天第t时段负荷相对第i天第0 时段负荷的相对误差为；则第i天第t时段的实际负荷可以表示为

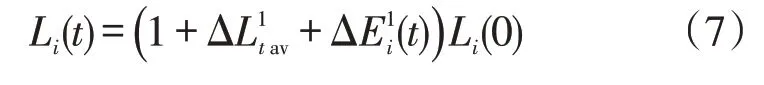
这时第i天第t时段负荷对应的预测误差又可以表示为

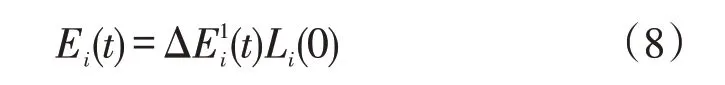
综合上面的分析可知，充分考虑外界因素，合理选择负荷变化率，能够有效提高负荷预测方法的精度，即为本文的研究依据。

2 基于变化趋势和气象因子的加权负荷预测方法

根据前面的分析，为了进一步提高电力负荷预测方法的精度，本文将充分考虑气象因子、合理选择负荷变化率，提出了基于变化趋势和气象因子的加权负荷预测方法，具体步骤如下：

（1）根据气象历史数据，对气温、湿度和天气类型3个气象因子进行归一化处理。

结合各类气象因子对电力负荷大小的影响，本文重点研究气温、湿度和天气类型3 个要素［13］。为保证各要素的统一性，需对各要素进行归一化处理［14—15］，但现有的方法归一化处理后，归一化数据处于0 到1 的闭区间内，即最大值对应1，最小值对应0，这样就使得归一化结果不能作为分母，限制了归一化方法的应用范围。基于此，本文提出了一种改进的归一化方法，该方法可将归一化数据控制在0到1的开区间内，则气温要素的归一化模型为

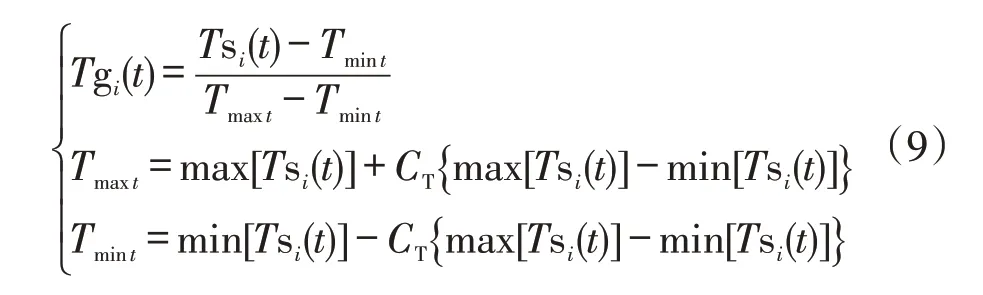
式中：Tsi(t)为所在区域第i天第t时段的气温实际值；Tgi(t)为所在区域第i天第t时段的气温归一化值；max[Tsi(t)]为所在区域第t时段历史最高气温；min[Tsi(t)]为所在区域第t时段历史最低气温；CT为气温归一化系数，根据式（9）可知归一化最大值为(1+CT)/(1+2CT)，归一化最小值为CT/(1+2CT)。归一化最大值和最小值随CT变化曲线如图1所示，显然归一化最大值随着CT的增加而减少，而归一化最小值随着CT的增加而增加，为了使归一化结果尽量分布在0到1之间，将CT取值定在0.05～0.45。

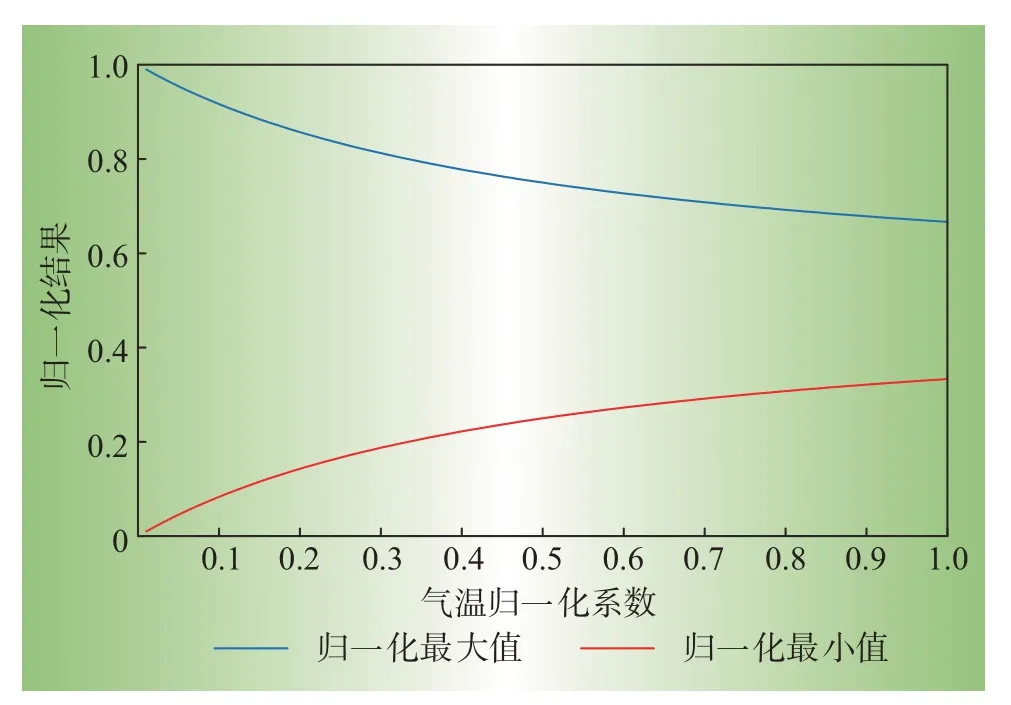
图1 归一化最大值和最小值随归一化系数的变化曲线Fig.1 Change curves of normalized maximum and minimum values with normalization coefficient

根据气温要素归一化模型，同理可得湿度要素归一化模型

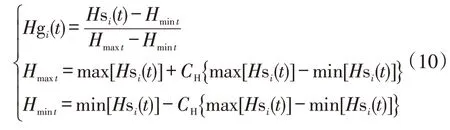
式中：Hsi(t)为所在区域第i天第t时段的湿度实际值；Hgi(t)为所在区域第i天第t时段的湿度归一化值；max[Hsi(t)]为所在区域第t时段历史最高湿度；min[Hsi(t)]为所在区域第t时段历史最低湿度；CH为湿度归一化系数，一般取值0.05～0.45。

考虑到天气类型一般包括晴天、多云、阴天和雨天等，属于定性变量，难以直接量化，因此在研究天气类型时，将定性变量天气类型等效为光照强度和降雨量2 个定量变量，则天气类型要素归一化模型可以表示为

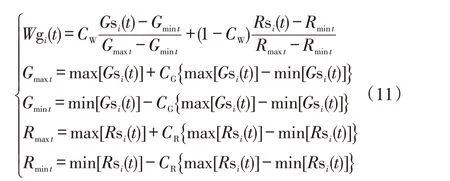
式中：Gsi(t)为变压器所在区域第i天第t时段的光照强度实际值；Ggi(t)为所在区域第i天第t时段的光照强度归一化值；max[Gsi(t)]为所在区域第t时段历史最高光照强度；min[Gsi(t)]为所在区域第t时段历史最低光照强度；CG为光照强度归一化系数，一般取值0.05～0.45；Rsi(t)为所在区域第i天第t时段的降雨量实际值；Rgi(t)为所在区域第i天第t时段的降雨量归一化值；max[Rsi(t)]为所在区域第t时段历史最高降雨量；min[Rsi(t)]为区域第t时段历史最低降雨量；CR为降雨量归一化系数，一般取值0.05～0.45；Wgi(t)为所在区域第i天第t时段的天气类型等效归一化值；CW为天气类型等效归一化系数，即为光照强度和降雨量的加权系数，故一般取值0～1.00。

（2）根据历史电力负荷数据，求解日内平均负荷变化率和点间平均负荷变化率。

研究电力负荷变化率时，本文将考虑日内负荷变化率和点间负荷变化率2 种情况。日内负荷变化率是指某日某时刻相对该日0 时刻的负荷变化率；点间负荷变化率是指某日某时刻相对该日前一时刻的负荷变化率，则日内平均负荷变化率可以表示为

式中：ΔLa(t)为第t时段所对应的日内负荷平均变化率。

根据日内平均负荷变化率模型，同理可得点间负荷变化率模型

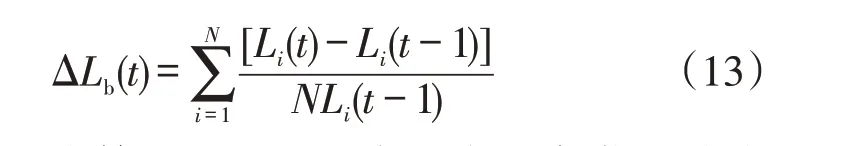
式中：ΔLb(t)为第t时段所对应的点间负荷平均变化率。

（3）根据日内负荷平均变化率和点间负荷平均变化率模型，建立加权负荷预测模型。

根据日内负荷平均变化率模型，可得电力负荷预测模型为

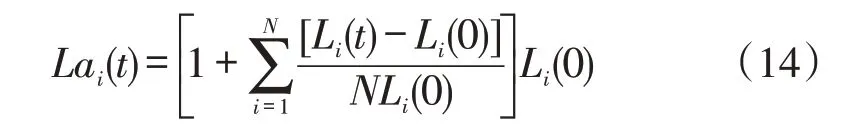
式中：Lai(t)为基于日内负荷平均变化率模型的预测结果。

根据点间负荷平均变化率模型，可得电力负荷预测模型为

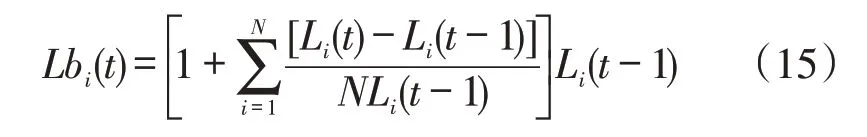
式中：Lbi(t)为基于点间负荷平均变化率模型的预测结果。

根据基于日内负荷平均变化率和点间负荷平均变化率预测模型，可建立加权负荷预测模型如下

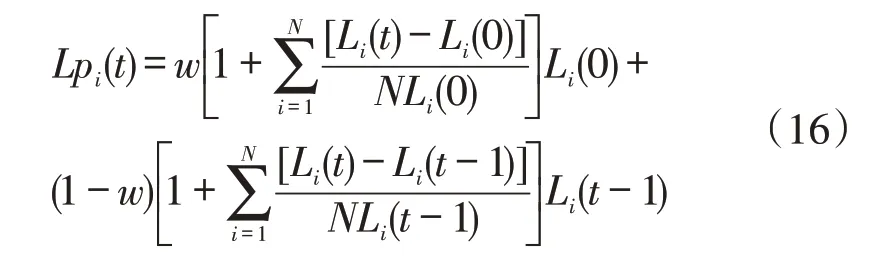
式中：Lpi(t)为加权负荷预测模型；w为比例系数。

（4）基于气温、湿度和天气类型3个气象因子，建立基于变化趋势和气象因子的加权负荷预测模型。

在基于日内负荷平均变化率和点间负荷平均变化率的加权预测模型的基础上，充分考虑气温、湿度和天气类型3 个气象因子的影响，建立修正预测模型如下

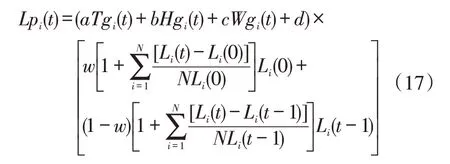
式中：a、b、c、d分别为电力负荷预测模型参数。

（5）基于最小二乘法的思想，建立考虑气象因子的加权负荷预测方法的参数优化模型，求解得到最优参数后，代入预测模型，即可实现电力负荷的预测。

利用历史电力负荷及其所在地区的历史气象因子，基于最小二乘法的思想［19—20］，即可建立参数优化模型如下

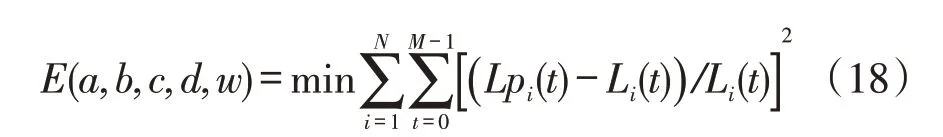
式中：M为日负荷数据点数。求解得到模型最优参数后，代入预测模型，即可实现电力负荷的预测与分析。

3 算例分析

为了验证文中电力负荷预测方法的有效性与可行性，以苏北某地区夏季六月、七月、八月前50个工作日的电力负荷数据作为研究对象，分析基于变化趋势和气象因子的加权负荷预测方法的计算过程。

3.1 气象因子归一化处理

结合式（9）、式（10）和式（11）对气温、湿度和天气类型3 个气象因子进行归一化处理，其中气象因子数据是指预测点的气象预报数据。根据前文的分析可知，归一化系数取值尽可能小，可以使得归一化结果分布在0 到1 之间，本文选择0.05～0.45 的最小值，故CT取值为0.05，CH取值为0.05，CG取值为0.05，CR取值为0.05，同时本文认为光照强度和降雨量2 个变量对天气类型的影响是同等重要的，故CW取值为0.50。图2 为典型日所对应的归一化前后温度曲线，其中归一化后温度曲线对应的温度值等于温度归一化值与当日最大温度值的乘积。

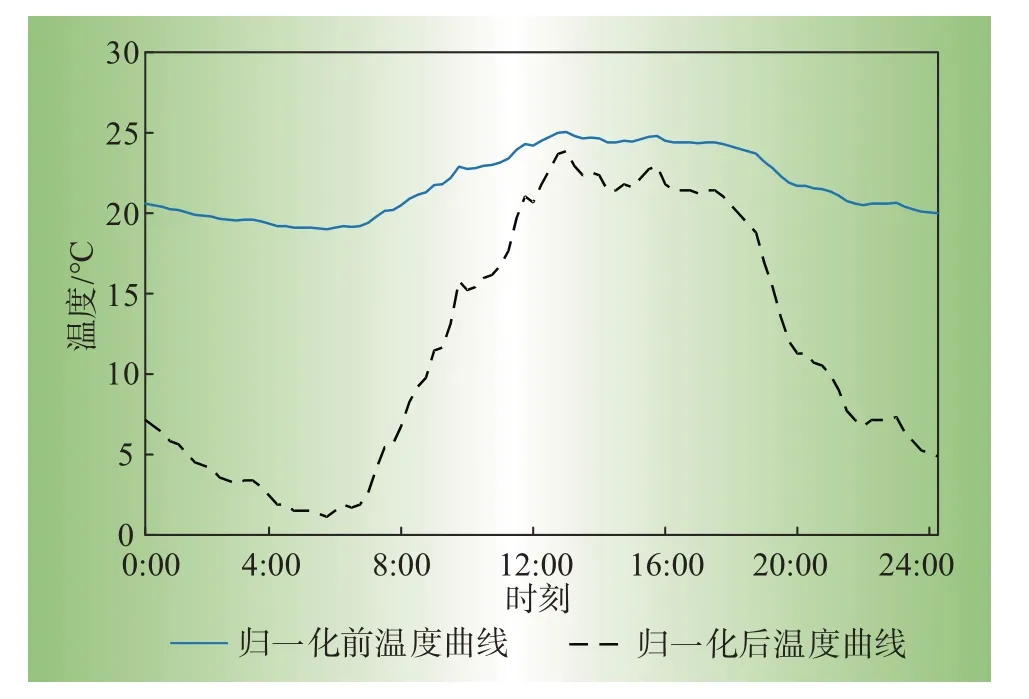
图2 典型日所对应的归一化前后温度曲线Fig.2 Normalized temperature curves before and after typical day

图3 为典型日所对应的归一化前后湿度曲线，其中归一化后湿度曲线对应的湿度值等于湿度归一化值与当日最大湿度值的乘积。

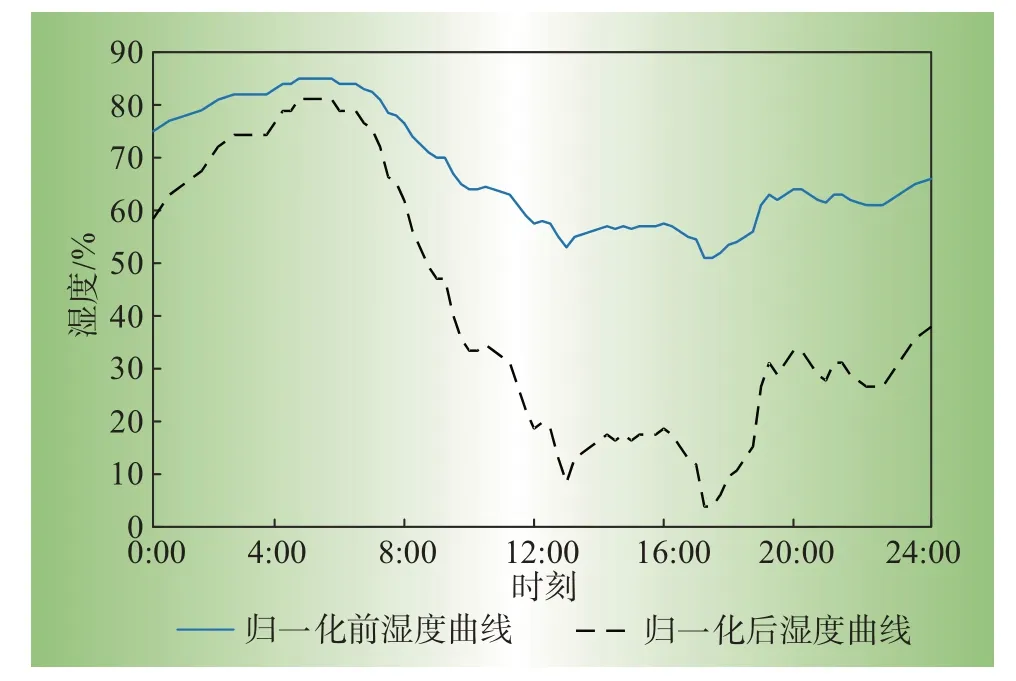
图3 典型日所对应的归一化前后湿度曲线Fig.3 Normalized humidity curves before and after typical day

典型日所对应的归一化后天气类型曲线如图4所示，由于光照强度和降雨量2个变量的量纲不同，不能直接进行运算，故图4 只给出了天气类型归一化后的曲线。

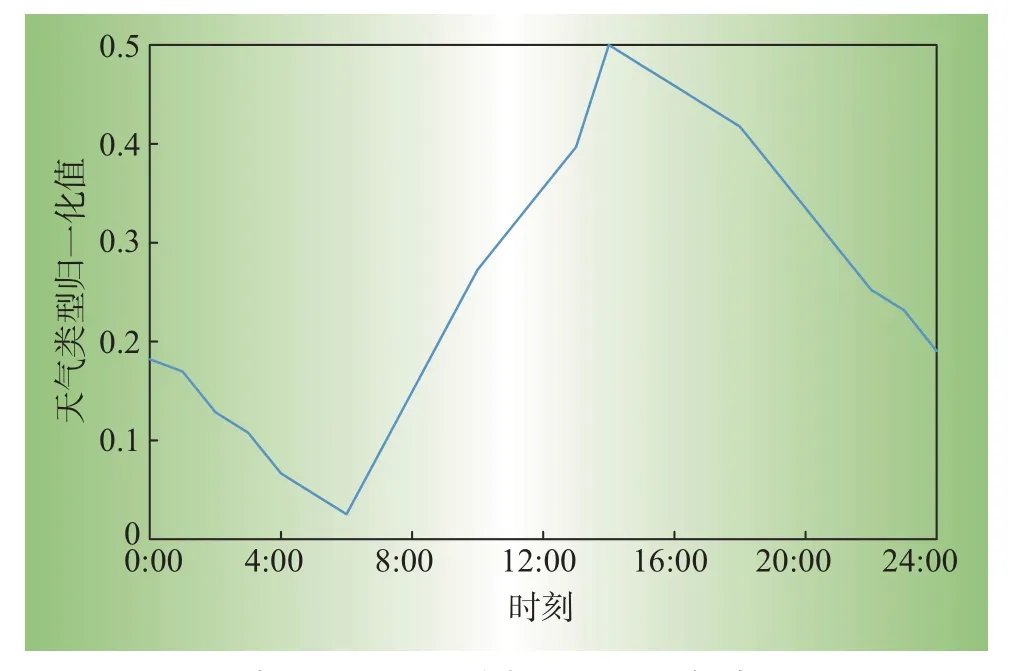
图4 典型日所对应的归一化后天气类型曲线Fig.4 Normalized weather type curve of typical day

3.2 平均负荷变化率求解

利用式（12）和式（13）即可求解得到日内平均负荷变化率和点间平均负荷变化率如图5所示。

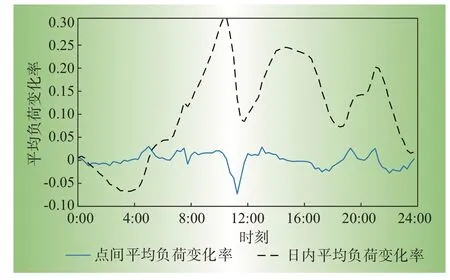
图5 日内平均负荷变化率和点间平均负荷变化率曲线Fig.5 Curves of daily average load change rate and average load change rate among points

3.3 模型最优参数求解

考虑到模型参数a、b、c分别表示温度、湿度和天气类型对负荷的影响，故3 种参数与负荷的相关性与模型参数存在一定关系，考虑到相关性大小取值为［-1,1］，故设a的取值范围为［-1:0.01:1］；b的取值范围为［-1:0.01:1］；c的取值范围为［-1:0.01:1］。本文采用气象因子对基于负荷变化趋势的预测方法进行修正，模型参数d作为一个修正因子，一般在0到1之间变化，故设d的取值范围为［0:0.01:1］。w作为基于日内负荷平均变化率和点间负荷平均变化率预测模型的比例系数，目标就是使得预测结果接近实际值。本文确定a、b、c、d范围后，利用该地区前40个工作日的电力负荷数据训练式（18），当a、b、c、d在各自取值范围内变化时，w在［-10,10］范围内，参数优化函数E(a,b,c,d,w)都能取得最小值，故确定w的取值范围为［-10:0.01:10］。最后基于最小二乘法的思想，采用MATLAB 软件实现，得到的最优参数结果为a=0.05；b=0.04；c=0；d=0.96；w=3.65。

3.4 预测结果分析

将表1 中最优参数值代入式（17），即可完成考虑气象因子的电力负荷预测模型的建立。利用上述建立的电力负荷预测模型计算该地区后10 个工作日的电力负荷数据，并与该地区实际电力负荷数据进行对比，验证模型的有效性，结果如图6所示。

图6 基于变化趋势和气象因子的加权负荷预测方法的预测结果Fig.6 Forecasting results of power load forecasting method considering meteorological factors

由图6 可知，基于变化趋势和气象因子的加权负荷预测方法的计算误差为3.41%，最小误差为1.69%，最大误差为6.28%，预测精度较高，能够满足实际生产需求。

同时为了验证本文所提出的基于变化趋势和气象因子的加权负荷预测方法相对基于变化趋势的电力负荷预测方法的优越性绘制了表1。表1 中基于变化趋势的电力负荷预测方法简称为方法1，基于变化趋势和气象因子的加权负荷预测方法简称为方法2。

表1 预测结果对比情况Table 1 Comparison of forecasting results

分析表1 可知，相对于基于变化趋势的电力负荷预测方法，本文所提出的基于变化趋势和气象因子的加权负荷预测方法，其平均相对误差较小，表明预测精度更高；其最小相对误差、最大相对误差以及相对误差标准差也都较小，表明预测数据更加平稳。

同时为突出预测方法的优越性，本文又采用了基于气象因子的线性回归法和基于气象因子的BP神经网络预测电力负荷，各种方法的预测结果如图7所示。

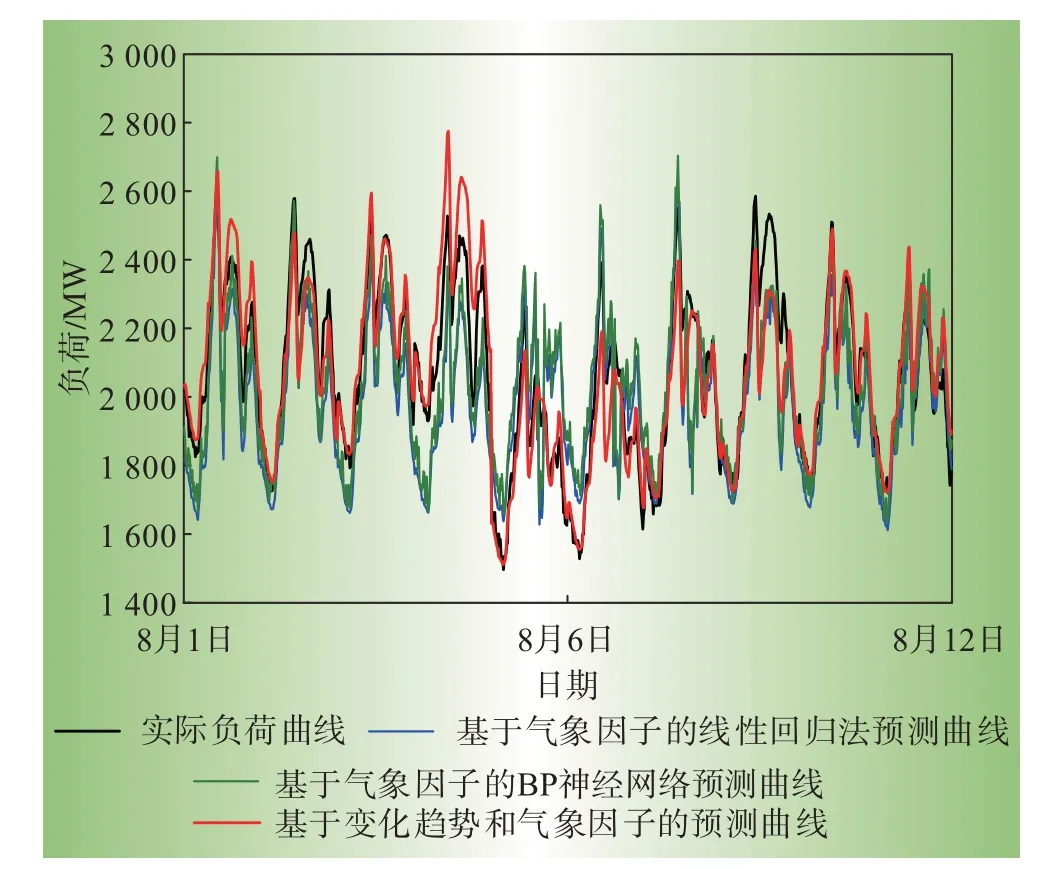
图7 各种方法预测结果对比Fig.7 Forecasting results comparison for various methods

分析图7可以得到以下结论：

（1）基于气象因子的线性回归法和基于气象因子的BP神经网络预测电力负荷的效果相似，这是因为2种方法都是基于气象因子与电力负荷的相关性，未考虑负荷的变化趋势。

（2）相比于基于气象因子的线性回归法和基于气象因子的BP神经网络，本文所提出的基于变化趋势和气象因子的加权负荷预测方法的预测结果更加接近实际负荷，这是因为该方法在预测电力负荷时，分别从日内平均负荷变化率和点间平均负荷变化率两个方面考虑了负荷变化趋势，同时基于气象因子对负荷变化趋势进行了修正，这样就使得负荷变化趋势更加接近真实值，即预测结果更准确。简单来说，相对其他2种基于气象因子的预测方法，本文所提出的方法充分考虑了气象因子和变化趋势，考虑的影响因子更多，预测效果更好，从而验证了该方法的有效性与可行性。

此外本文还对近期电力负荷预测方法及气象因子法以外的预测方法进行了充分研究，采用文献［8］的指数平滑法、文献［9］的支持向量机、时间序列法进行了预测，其中支持向量机是基于气象因子预测负荷，而指数平滑法和时间序列法则是基于电力负荷随时间变化趋势来预测负荷，结果如表2 所示，显然本文所提出方法的预测精度要优于指数平滑法和时间序列法，但和支持向量机的方法相当，这表明本文所提出方法具有一定预测精度，能够满足现场实际应用要求，进而验证了方法的可行性。

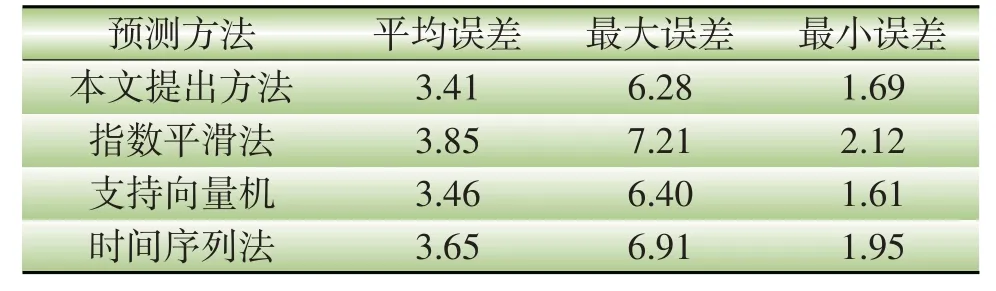
表2 预测误差统计表Table 2 Forecasting error statistics table%

3.5 预测模型泛化能力验证

为验证预测模型的泛化能力，本文采用交叉验证方式，将苏北某地区夏季六月、七月、八月前50个工作日均分为5个部分，其中将第2—第5部分作为训练集，第1 部分作为测试集，称为试验1；将第1、第3—第5 部分作为训练集，第2 部分作为测试集，称为试验2；将第1和第2、第4和第5部分作为训练集，第3部分作为测试集，称为试验3；将第1—第3、第5部分作为训练集，第4部分作为测试集，称为试验4；将第1—第4部分作为训练集，第5部分作为测试集，称为试验5。分别对上述5次试验进行计算得到试验结果的平均相对误差为3.42%，且5次试验的预测结果都十分相近，最大相差为0.14%，从而验证了本文所提出方法的泛化能力。

4 结束语

（1）本文分析了基于变化趋势的电力负荷预测方法存在的2 个问题：未充分考虑外界因素对电力负荷趋势变化的影响和预测电力负荷时存在误差累计的可能。

（2）在充分考虑日内平均负荷变化率和点间平均负荷变化率的基础上，基于气温、湿度和天气类型3 个气象因子，提出了基于变化趋势和气象因子的加权负荷预测方法。

（3）以苏北某地区电力负荷数据作为研究对象，采用本文所提出的基于变化趋势和气象因子的加权负荷预测方法进行了预测，算例验证了方法的有效性。