真空玻璃的应力分析及强度设计

刘小根，齐 爽，孙与康

(1.中国建筑材料科学研究总院有限公司，绿色建筑材料国家重点实验室，北京 100024；2.中国国检测试控股集团股份有限公司，北京 100024)

0 引 言

建筑幕墙和门窗玻璃区域是能量损耗最严重的部位(约占60%)[1]，因此，提高门窗幕墙玻璃的保温隔热性能是降低建筑能耗的重要举措之一。真空玻璃采用热水瓶原理，基本去除了空气传导和对流带来的热传输，提高了玻璃构件的隔热性能，其产品是继单片玻璃、中空玻璃之后，备受国际推崇的第三代门窗节能玻璃，是近期和未来玻璃领域重要发展战略之一[2]。

因真空玻璃结构特殊，制备后的真空玻璃产品本身存在残余应力，造成了其原始强度降低。在服役过程中，真空玻璃还受到环境温度、风载荷、振动及冲击载荷等作用，在以上多重载荷作用下，易造成真空玻璃破裂失效。据统计，建筑物上的真空玻璃破裂率往往高于其他玻璃品种(图1为真空玻璃服役过程中的典型破裂形貌)，这给真空玻璃生产与工程应用造成了较大损失，甚至对其推广应用造成较大负面影响。

图1 典型真空玻璃破裂形貌

合理的结构设计可以优化真空玻璃内部应力，降低其不利影响。针对应力诱导真空玻璃破裂的这一问题，悉尼大学[3]真空玻璃团队早在20世纪90年代就对真空玻璃在大气压差和温差作用下的应力进行了一系列的理论分析、数值模拟和实验验证。英国 Ulster 大学Simko等[4]构建了含有支撑和封边的完整有限元模型，分析了低温封边技术在真空玻璃内部产生的应力。Wullschleger等[5]采用三种不同类型钢化真空玻璃模型，研究了支撑物对钢化真空玻璃横向剪切刚度和挠度的影响。蔺海晓等[6]采用赫兹接触理论，对钢化真空玻璃球形支撑压痕应力场进行了分析。蔡冬等[7]基于弹性理论和ANSYS分析了支撑物缺位对弧面钢化真空玻璃支撑应力的影响。李彦兵等[8]分析了支撑点间距对钢化真空玻璃力学特性的影响。刘小根等[9-13]对真空玻璃的支撑压痕控制准则、温差作用应力、风压作用应力、支撑物缺位影响及真空玻璃结构优化及工程应用理论等方面也进行了较详细探讨,有力支撑了真空玻璃新产品研发及其结构优化与工程应用,但以上分析结果均未考虑持久应力作用下真空玻璃强度设计问题。

本文根据真空玻璃结构特征，分析了大气压差、温差及风载荷作用下真空玻璃的应力分布，给出了最大弯曲拉应力定量计算公式。基于结构抗力设计方法，分析了长期和短期应力协同作用下真空玻璃的承载性能及强度设计，以指导真空玻璃工程安全可靠应用。

1 真空玻璃应力理论分析

1.1 大气压作用下真空玻璃应力分布

真空玻璃两基片之间存在许多支撑物，以抵御外界大气压作用下两基片产生的过大变形，防止其相互接触。在此情况下，会在真空玻璃内部产生应力,其中分布在支撑点处玻璃板上(外)表面处的弯曲拉应力最大[13]。假设支撑物横竖支撑阵列间距均为定值a，以任一支撑物为中心，取出一个正方形单元，且其边长为a。根据其对称性及变形特征，可将正方形玻璃单元受力特征视为四边固支弹性矩形薄板，且空气面受一个大气压q0作用，真空面受支撑物集中应力F作用，受力分析图如图2所示。根据弹性薄板理论，玻璃单元最大弯曲拉应力分布在支撑点处玻璃上表面，计算公式如下[13]：

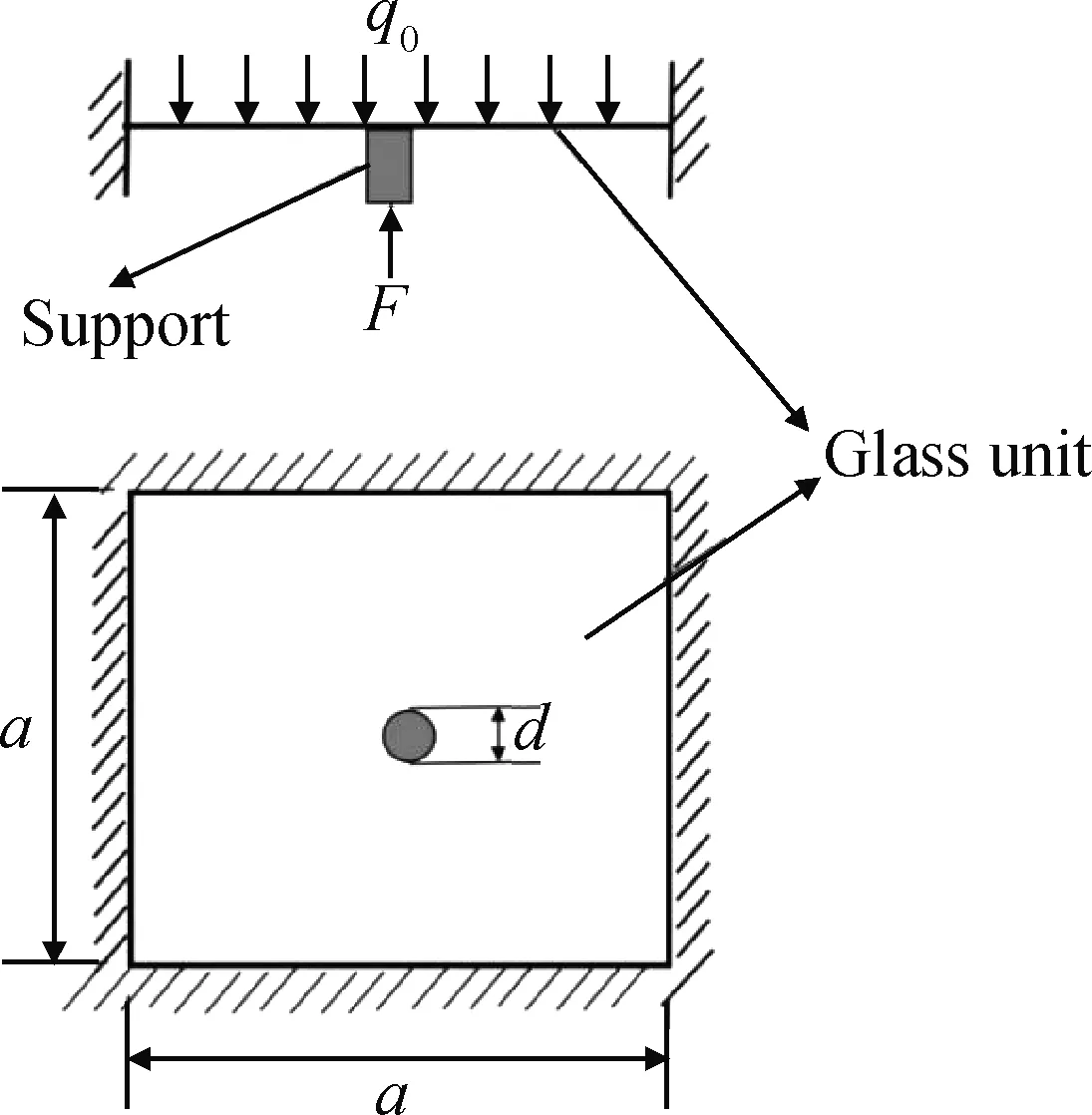
图2 玻璃单元受力分析示意图

(1)

式中：σa为大气压差作用下玻璃的最大弯曲拉应力；F=q0a2；h为真空玻璃基片厚度；v为玻璃的泊松比，取值为0.24；d为支撑物直径。

1.2 温差诱导真空玻璃应力分布

服役过程中，由于真空腔体隔断了热流的传导，使得真空玻璃内、外两基片存在较大的温差，导致其膨胀长度不匹配。因真空玻璃的内、外两片玻璃四周被低熔点玻璃熔封在一起，两片玻璃边缘伸缩时相互制约，从而造成真空玻璃整体产生球面弯曲变形并产生弯曲拉应力。

设真空玻璃内、外两片玻璃温差为ΔT，玻璃基片线膨胀系数为α。在温差作用下，任取弯曲球面真空玻璃内片玻璃的单位长度dl为研究对象，与该长度(弯曲角度θ)对应的外片玻璃的长度为dl+αΔTdl。设内片玻璃横截面中心距球面球心O的距离为R(球面的曲率半径)，忽略真空玻璃间隙层厚度(间隙层厚度远小于玻璃基片厚度)，则外片玻璃横截面中心距球心O的距离为R+h(见图3)。

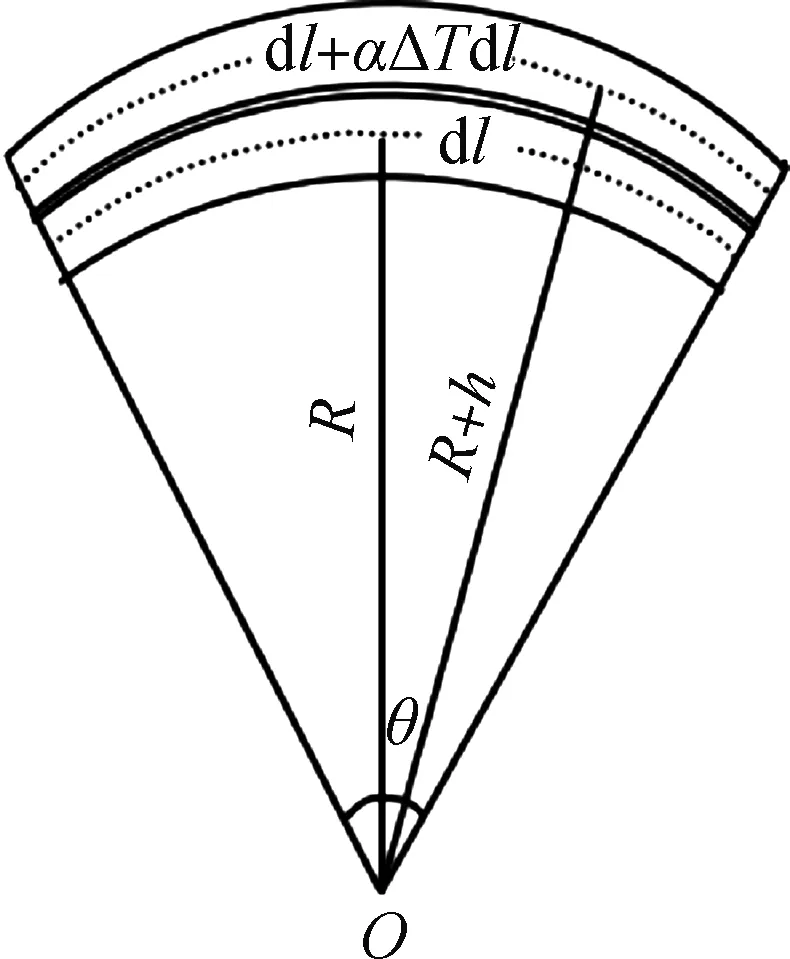
图3 温差作用下真空玻璃内、外片变形协调示意图

根据变形协调关系，同时考虑玻璃板的泊松效应，则真空玻璃内、外片玻璃在任一方向的单位长度的变形协调满足如下关系：

(2)

式(2)可简化为:

(3)

由式(3)可以看出，真空玻璃的弯曲曲率半径与玻璃基片的厚度成正比，与玻璃基片的线膨胀系数及内、外片温差成反比，与真空玻璃的长、宽尺寸无关，曲率半径越小，说明真空玻璃弯曲越厉害，造成的危害就越大。

真空玻璃发生球面弯曲，其最大弯曲拉应力发生在温度较高一面的玻璃凸面，因弯曲曲率相同，所以最大弯曲拉应力也处处相等。如果不考虑封边焊料的作用，真空玻璃弯曲曲率与弯矩满足公式(4)[10]:

(4)

式中:M为玻璃基片的弯曲截面系数;I和W分别为真空玻璃基片的截面惯性矩和抗弯截面系数;E为玻璃的弹性模量(钢化玻璃一般取值为72 GPa);σT为温差作用下玻璃的最大弯曲拉应力。

将式(3)代入式(4)，得到：

(5)

1.3 风压作用下真空玻璃应力分布

应用于建筑物上的真空玻璃，风压致损是一个需要重点关注的问题。对于真空玻璃这种特殊结构，由于其厚度方向上非连续(两片玻璃之间有间隙层)，所以在进行弯曲拉应力或挠度计算时，不能采用其名义厚度(两基片厚度加真空层厚度)代入已有公式进行计算。对于边缘支承的真空玻璃，其弯曲特性具有如下特征：(1)真空玻璃两片玻璃变形协调，且每片玻璃均有弯曲中性轴；(2)风载荷作用下最大弯曲拉应力分布在真空玻璃凸面的板中心位置；(3)弯曲状态下，两基片之间的支撑物不传递剪力，但基片边缘封接玻璃粉具有传递剪力作用。

不同开口形状与开口不同的加强形式的应力集中程度如图7所示，开口位置的主要载荷形式为拉压载荷，说明风机塔筒结构主要受弯曲载荷作用。从图7可以看出，在孔边缘焊接加强结构会大幅度降低开孔边缘的应力峰值，但是对开口结构的疲劳强度却未必有改善。不同开口的应力集中情况与疲劳损伤大小如表5所示，从表中可以看出，虽然增加套筒降低了开孔边缘的应力集中，但是疲劳寿命却降低了，主要原因是引入了焊接，增加了开口结构疲劳开裂的风险。所以一旦出现疲劳强度不足时，除非考虑优化开口形式，很难找到其他更加经济的方法，所以在单桩基础上开口，需要对疲劳强度做细致的分析，确保开口结构具有足够的疲劳强度。

为便于计算，实际工程计算时，仍把真空玻璃简化为一块平板，其厚度按等效厚度计算，对于四边支承的真空玻璃板，风载荷作用下，其最大弯曲拉应力分布在板中心，计算公式如下[11]：

(6)

其中：σw为风载荷作用下玻璃的最大弯曲拉应力；q为作用在真空玻璃上的风载荷值；teq为真空玻璃等效厚度；φ为弯曲系数，与边长比l/b有关，l为矩形真空玻璃板短边边长,b为真空玻璃板的长边边长，边长比按表1选取。

表1 φ值

2 结果与讨论

2.1 支撑物支撑间距及基片厚度对大气压作用下真空玻璃应力影响

以直径d为0.3 mm的支撑物为计算对象，通过改变真空玻璃基片厚度及支撑物支撑间距，按式(1)计算得到了不同基片厚度及不同支撑间距下的玻璃表面最大弯曲拉应力变化(见图4)。由图4(a)可以看出，在给定基片厚度情况下，随着支撑间距的增大，其玻璃表面最大弯曲拉应力也呈近似线性关系增长。由图4(b)可以看出，在支撑物间距不变情况下，玻璃表面最大弯曲拉应力随基片厚度增大呈指数式下降趋势。显然，增大玻璃基片厚度，能明显降低玻璃表面最大弯曲拉应力。因此，玻璃基片越厚，其支撑物布放间距可以适当提高，从而有利于进一步降低真空玻璃因支撑物带来的热传导。

图4 支撑间距及基片厚度对真空玻璃最大弯曲拉应力影响关系曲线

2.2 温差对真空玻璃应力影响

由式(5)可以看出，温差引起的最大弯曲拉应力与玻璃基片厚度及长宽尺寸无关，但与膨胀系数有关。温差与其引发的玻璃最大弯曲拉应力呈线性关系。

为验证理论分析结果的准确性，选择厚度为5 mm+5 mm，长宽尺寸为800 mm×800 mm的真空玻璃试样进行试验。将真空玻璃置于控温箱上，通过调节控温箱温度以加热真空玻璃一面，真空玻璃另一面朝室温面。在真空玻璃两面板中心位置贴上应变片和热电偶，以测量真空玻璃两面温差和因温差引起的应力。图5为由式(5)计算及试验测试结果获得的不同温差下的最大弯曲拉应力变化，显示了理论与测试结果基本吻合，且温差值与其引发的真空玻璃最大弯曲拉应力呈线性关系。虽然基片厚度对温差引起的最大拉应力无影响，但增大基片厚度，有利于降低温差引起的球面弯曲变形，从而降低因温差导致的真空玻璃边缘变形量，以减小真空玻璃边缘与支承槽口之间因相互挤压而引发的附加应力。

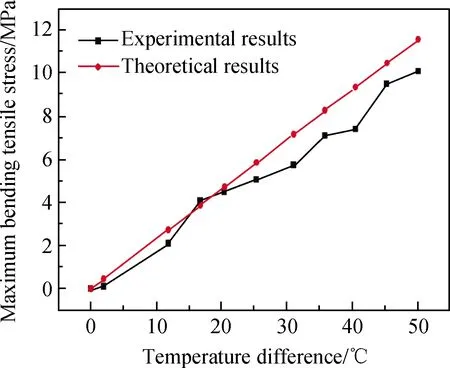
图5 温差引起的真空玻璃最大弯曲拉应力理论和试验结果对比

2.3 真空玻璃抗风压性能及等效厚度

风压作用下，可按式(6)计算四边支承的真空玻璃最大弯曲拉应力，计算时采用了等效厚度概念。在同样条件下，真空玻璃产生的最大弯曲拉应力或变形与单片玻璃相同，此时单片玻璃的厚度即为该真空玻璃的等效厚度。

图6为分别采用长宽尺寸均为1 000 mm×1 000 mm，6 mm厚的单片玻璃、8 mm厚的单片玻璃、4 mm+4 mm厚的真空玻璃及4 mm+1.52 mm PVB胶片+4 mm夹层玻璃，在四边支承情况下进行均布负压试验，获得的板中心最大弯曲拉应力。由图6可以看出，在同样载荷作用下，夹层玻璃表面最大弯曲拉应力最小，真空玻璃最大弯曲拉应力最大，说明外载作用下真空玻璃承载性能不如其他两种玻璃。

图6 均布负压作用下不同玻璃表面最大弯曲拉应力

真空玻璃结构特殊，难以通过理论准确确定其等效厚度，但通过试验可以准确确定其等效厚度，等效厚度可按式(1)计算：

(7)

式中：teq为真空玻璃等效厚度；σp和σv分别为相同条件下获得的单片玻璃和真空玻璃的最大弯曲拉应力；t为单片玻璃的厚度。

根据图6测量的结果，按照式(7)进行计算，4 mm+4 mm真空玻璃的等效厚度约为7.5 mm，其他规格的真空玻璃等效厚度均可按上述方法获得。将真空玻璃等效厚度代入式(6)，即可得到给定风压作用下真空玻璃的最大弯曲拉应力。

2.4 长期和短期载荷协同作用下真空玻璃强度设计

按照现行国家标准《建筑结构可靠性设计统一标准》(GB 50068—2018)[14]的规定，结构承载能力的极限状态设计及正常使用极限状态设计均应区分不同的设计状况以进行作用(荷载)组合或作用(荷载)效应组合，并取最不利的效应设计值进行结构设计。真空玻璃在服役过程中，会受到大气压差、温差及风压作用形成的应力协同作用，这三种应力在板中心及边部的叠加应力可超过玻璃强度设计值。按我国香港地区现行标准《Code of Practice for Structural Use of Glass》[15]规定，载荷持续时间超过1 d，则可定为长期载荷作用，大气压差及温差导致的应力为长期作用;风载荷作用时间一般为3 s，其导致的应力为短期作用。因此，真空玻璃受长期和短期应力协同作用。

对于任何应力的协同作用，其导致的玻璃损伤均可进行累加。长期应力作用下，会导致玻璃产生静态疲劳，造成玻璃强度值下降。对于承受不同应力作用时间的玻璃构件，宜分别计算其效应设计值，并按式(8)校核：

(8)

式中：σ短、σ长分别为玻璃构件受到短期应力和长期应力时的设计值；f短、f长分别为玻璃构件在短期载荷和长期载荷作用下的强度设计值，其取值见表2[16]。

表2 玻璃的强度设计值

将式(1)及式(5)计算的应力之和代入式(8)中的σ长，将式(6)计算的应力代入式(8)中的σ短，即可判断真空玻璃强度或承载性能是否满足要求。

3 结 论

(1)在给定基片厚度情况下，随着支撑间距的增大，真空玻璃最大弯曲拉应力呈近似线性增长，在支撑物间距不变情况下，真空玻璃最大弯曲拉应力随基片厚度增大呈指数式下降趋势。

(2)温差引起的最大弯曲拉应力与玻璃基片厚度及长宽尺寸无关，但与膨胀系数有关，温差值与其引发的真空玻璃最大弯曲拉应力呈线性关系。

(3)相同条件下，真空玻璃抗风压性能弱于与其等厚度的单片玻璃,实际工程计算时，宜把真空玻璃简化为一块平板，其厚度按等效厚度计算。真空玻璃等效厚度可通过试验确定，4 mm+4 mm规格真空玻璃等效厚度约为7.5 mm。

(4)长期和短期应力协同作用下，宜分别计算不同应力作用时间下真空玻璃的效应设计值进行校核。