基片表面倾斜及衍射对激光会聚原子沉积条纹的影响
张宝武,张超超,刘若男,王道档,沈小燕,余桂英
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
原子共振跃迁频率具有稳定性高、测量精度高、可复现性好等优点,已经为人类时标提供了稳定准确的秒长,助推人类计量学迈入“秒制”的广阔领域[1]。这必将更好地促进量值传递溯源扁平化和多极化的发展,为物理学的精密测量、航空航天控制、快速数字通信、生物医学等领域提供更好的时标[2]。
激光会聚原子沉积技术(Laser Focused Atomic Deposition,LFAD)就是将原子共振跃迁频率应用于纳米量值传递溯源的典型案例。经过近30年的发展,它已经从最初的钠原子扩展至铬、铝、铁和镱等原子[3-4],从最初的一维光栅结构扩展至二维、三维,从纯粹的长度传递溯源扩展至角度标准传递溯源[5]。这些多角度、多层面的发展方向都是基于LFAD的基本原理,即高稳定性的单频激光沿着沉积基片表面传播,经反射镜原路反射后形成稳定的驻波场。在合适的激光强度和频率失谐(一般蓝失谐几百兆赫兹之内)的情况下,每个激光驻波波节或者波腹就会呈现会聚透镜的功能,使准直原子束穿过它的时候发生会聚效果[6-8],进而使基片表面上沉积出能够复现激光驻波场的条纹或者多维结构[9-14]。研究结果表明一维LFAD形成的光栅结构的平均相邻条纹间距在10-5量级上能够非常精确地复现激光驻波场周期[3]。二维LFAD形成的点状结构在量级上能够非常精确地将平面镜间的宏观角量传递至纳米角量[5]。
研究表明,基片与会聚光场之间的关系对沉积结构质量参数的影响很大[15-17],为实验提供了很好的指导。但是,实验条件的提高,研究者发现沉积结果和理论分析之间存在差距。这其中主要的因素就是基片端面的衍射效应和基片与驻波中轴线之间平行度(垂直于原子束中轴线的截面内)。为此,本文将有机联合这两方面的影响因素,深入地仿真研究驻波场轴线与基片表面非平行下基片衍射对沉积条纹的影响。
1 理论分析
本文仿真所依据的实验装置和理论原理在文献[12]中已有详细的描述,此处直接引用其中一些关键的内容。
LFAD中激光束(Focusing laser beam)、基片(Substrate)和反射镜(re)之间的位置关系如图1,其中准直原子束沿着z轴方向自上而下传播,会聚激光束沿着x轴自左向右传播。激光被反射镜原路反射后与其自身叠加,构成汇聚驻波场。入射激光的束腰严格位于反射镜的镜面上,并且入射激光的中轴线严格垂直于反射镜表面。基片右端面与反射镜相接触的位置处正好与激光轴线重合。x0表示基片表面x轴上某一个特定的垂轴截面的坐标。α表示基片表面与驻波轴线间的夹角,记顺时针为正。
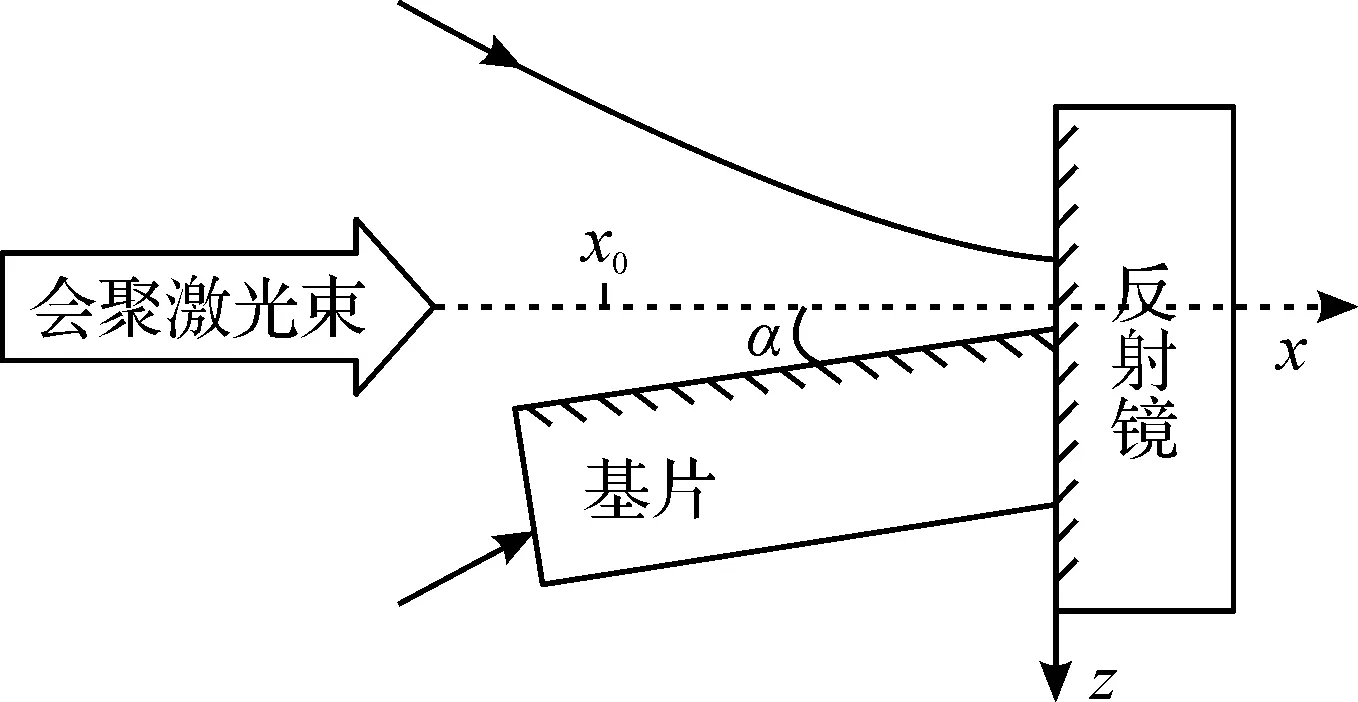
图1 激光束,基片和反射镜之间的位置关系
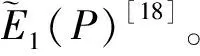
(1)
2 仿真结果和讨论
2.1 仿真参量
2.2 光学势能的仿真
图2为不同x0位置处,基片倾斜角α=±1mrad时,基片衍射与非衍射条件下,光学势能沿着z方向的变化情况。
以上三张仿真图都同时给出了衍射和非衍射情况下的势能分布。从中可以总结出如下结论:1)无论基片相对于激光中轴线如何倾斜,会聚激光都会因为基片左端面的切割而产生衍射效应;2)当α=1mrad时,激光将被基片左端面阻挡,使基片表面处于基片左端面的阴影区中,因此,非衍射条件下基片表面上z∈[-0.05ω0,0]的区域内存在一个零光学势能区;而衍射效应将使光学势能填满此区域。当α=-1mrad时,基片表面将被激光照射,所以不存在零光学势能区;3)与α=-1mrad相比,基片在α=1mrad时切割激光束比较多,从而进入到基片表面的光强较小。这样,不管光衍射与否,α=1mrad时的光学势能都是小于α=-1mrad时的光学势阱。4)基片衍射导致光学势能的峰值都向z轴的负方向产生位移。
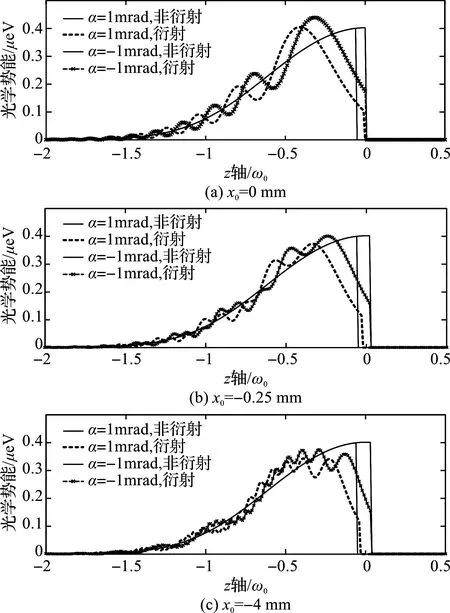
图2 不同x0位置处,基片倾斜角α=±1mrad时,基片衍射与非衍射光学势能沿着z方向的变化情况
2.3 铬原子运动轨迹的仿真
图3为不同x0位置处,基片倾斜角为α=±1mrad时,衍射与非衍射原子轨迹。图中所有实线是衍射条件下的轨迹,虚线是非衍射条件下的轨迹。图3中各种情况下的原子运动轨迹几乎相同,都是在光学势阱的作用下向着波节处会聚。这其中的细微差别在于:1)同一个倾角下,衍射时的运动轨迹在接近基片时弯曲得更厉害,即比非衍射时的运动轨迹提前会聚了,这主要来源于基片衍射使光强提前了,并且有强度的增加;2)同一x0处,α=-1mrad条件下的运动轨迹与α=1mrad条件下的相比,在基片表面附近显得更加弯曲。这主要在于α=-1mrad时,基片上表面全部被激光照射,基片阻挡掉的激光较小,因而基片表面上的光学势阱会更大。

图3 为不同x0位置处,基片倾斜角为α=±1mrad时,衍射存在与否原子轨迹
2.4 铬原子沉积条纹的仿真
图4为不同x0位置处,基片倾斜角为α=±1mrad时,衍射与非衍射原子沉积条纹。图中所有实线是衍射条件下的轨迹,虚线是非衍射条件下的轨迹。图4显示不同的x0位置处都会形成沉积条纹。不管基片倾斜角如何,随着x0远离反射镜,衍射条件下的沉积条纹中心相对于非衍射条件下的有一定的偏移,且都是向着|x0|偏大的方向偏移。与此同时,沉积条纹的峰值和半高宽都有一定的变化。
图5更加清晰地反映了条纹半高宽、条纹峰值和条纹峰值位置相对于波节的偏移量随x0的变化情况。图5(a)显示在倾角为α=1mrad的时候,不管衍射与否条纹半高宽随着|x0|的增大都有增大的趋势,而在α=-1mrad的时候条纹半高宽却几乎保持不变。这主要是因为α=1mrad的时候基片切割激光束较大,基片表面所接收到的光强减弱,进而对原子运动轨迹作用减弱,所以原子最终的落脚点相对弥散开来。另外,衍射条件下,条纹的半高宽略大于非衍射时的条纹半高宽。这主要是因为衍射使光势能的最大值提前了,也就是说衍射使原子运动轨迹会聚点提前了,进而造成原子最终的落脚点出现了一点的弥散。
图5(b)显示在倾角为α=1mrad的时候,不管衍射与否条纹峰值随着|x0的增大都有减小的趋势,而在α=-1mrad的时候条纹峰值却有增大的趋势。这主要还是来源于α=-1mrad能够使基片表面上获得更多的激光能量,进而提高会聚势能,提高会聚能力。

图4 为不同x0位置处,基片倾斜角为α=±1mrad时,衍射存在与否原子沉积条纹

图5 原子沉积条纹参数随x0位置的变化
图5(c)显示铬原子沉积条纹的峰值位置相对于波节的偏移量随着x0的变大趋向单调增大。非衍射条件下,在x0的变化范围内有4 nm的增大量;在衍射条件下,在x0的变化范围内有15 nm的增大量。
3 结 论
全文综合考虑基片表面相对于激光中轴线的倾斜度和基片端面对激光的衍射效应,对会聚场的光学势阱、原子运动轨迹和沉积条纹等进行了仿真实验。仿真结果显示基片端面会对会聚光场产生衍射效应,基片表面相对于驻波中轴线倾斜方向不同时,基片表面光学势阱分布不同,沉积条纹会展宽,沉积条纹的峰值相对于波节的偏移量具有单一方向的增大。
——《势能》

