基于扩展贝塞尔拟合模型的连续波穿墙雷达目标定位算法
丁一鹏 高山流水 郭学斌 厍彦龙
(中南大学物理与电子学院,湖南长沙 410083)
1 引言
近年来,利用多普勒穿墙雷达对人体目标进行定位跟踪在军事和民用领域具有广泛的应用背景[1-2]。研究成果表明,为了实时高效得对目标进行定位,准确估计目标的瞬时频率(Instantaneous Frequencies,IFs)具有重要作用。为了实现这一目标,目前最常用的方式是采用时频分析技术,通过提取时频平面上的最大值作为目标时频轨迹[3]。
然而在实际应用中,连续波穿墙雷达的目标探测主要存在的难题是:当检测多个目标,且不同目标间具有足够接近甚至重叠的瞬时频率时,目标的瞬时频率可能出现无法被准确的估计,从而导致定位结果误差较大,甚至无法定位[4]。针对上述问题,本文提出一种基于扩展贝塞尔模型的Hough 变换目标定位算法。该算法基于扩展贝塞尔拟合模型,通过动态调整两个参数拟合实际的目标频率曲线,特别是解决非线性、非对称曲线的拟合问题,并结合多普勒定位算法完成对目标的实时定位。实验结果表明,该算法有效地抑制频率模糊问题,提高了多普勒穿墙雷达对运动的人体目标的定位精度。
2 多普勒穿墙雷达传统定位方法及存在的问题
2.1 穿墙雷达目标定位算法
探测人体目标的过程中,主要利用的是最紧凑的双频多普勒穿墙雷达系统[5]。该系统由一个发射机(Tx)和两个接收机(Rx1 和Rx2)组成,其天线阵列结构如图1所示。
雷达的载波频率分别为f1和f2,接收机的距离为d,当目标处于当前位置时,h为两个天线入射波散射离开目标到达路径长度差,θ是目标的方向角。根据传播路程差可以计算出两个接收机输出信号相位差如下:
式中,λ1是载频f1分量对应的波长;
由此可得出目标的方位角:
式中,f1Rx1和f1Rx2分别为接收机Rx1 和Rx2 在载波频率为f1的载波下接收回波信号的瞬时频率,φθ为上述两信号的初始相位差。
光速为c,当目标距离接收机距离为R时,回波信号在两个载波频率下的相位变化为:
因此,可求得目标距离为:
其中f2Rx1为接收机Rx1 在载波频率为f2的载波下接收的回波信号的瞬时频率;φR为接收机Rx1 在不同频率下接收回波信号的初始相位差。
根据得出的方位角θ和距离R,可转化为笛卡尔空间坐标系:
轨迹合成算法用于根据目标距离和角度信息,在二维平面对目标进行定位。可以将目标的空间坐标确定为(X,Y),然后合成目标运动轨迹。
2.2 目标瞬时频率传统估计算法
(1)基于STFT的目标瞬时频率估计算法
在利用多普勒雷达系统实时探测人体目标的应用中,由于人体目标的回波信号为非平稳信号,人体目标的运动状态具有随机多变的特点,并且探测有实时性的需求,所以通常采用短时傅里叶变换技术(STFT)。
STFT的本质就是加窗的傅里叶变换,通过窗函数对信号进行处理,然后通过傅里叶变换对每一时段的信号进行分析处理[6]。短时傅里叶变换可以通过以下公式表示
式中,η(t)表示窗函数,τ表示时延,由于窗函数的移动,对时域信号R1(t)进行分割,这使得傅里叶变换有了局部的特性。通过分析可知,提高时间分辨率的代价是要求窗长尽量的短,但同时也降低了频率分辨率。这一矛盾使得短时傅里叶变换不能获取良好的时频分辨率。此外,通过短时傅里叶变换算法联合多普勒定位算法进行对人体目标的定位时,由于短时傅里叶变换的低时频分辨率的问题,导致连续波穿墙雷达对目标定位的精度较低。尤其是定位多个人体目标时,多个回波信号的瞬时频率有时会出现距离相近甚至交叉重叠的情况,由短时傅里叶变换分析得出的瞬时频率会有模糊现象,导致频率特征提取不准确,从而影响雷达系统在目标定位领域的应用。
(2)基于传统模型的Hough 变换目标瞬时频率估计算法
Hough变换一种能够将整体特征的检测转化为局部特征检测的有效方法,通过其沿目标回波信号的瞬时频率(IF)轨迹累积信号能量的能力,可以有效地识别和提取目标回波信号中的所需分量[7]。
所述发射机接收回波调解后的信号表示为:
其中,ak为第k个信号的幅度,fdi,k(t)是对应于载波频率fi的第k个目标分量的多普勒频率,φk=4πfiRk0/C是第k个信号回波初始相位,c是光速。
当利用雷达系统对人体目标检测时,对于包含k个分量的回波信号s(t),它可以表示为
式中si(t)是第i个回波分量,振幅为ai,fdi为第i个目标的IF。为了利用Hough 变换估计第i个目标的IF,首先要建立合适的频率拟合模型F(Z,t),Z为一组模型参数。该模型用于表示回波分量的IF 变化[8-9]。利用拟合模型解调回波信号s(t),然后利用傅里叶变换可得
如果将式(9)代入式(10)中,可以看出,在理想情况下,当fdi(t)=F(Z,t)时,所构造的模型完全拟合目标回波分量的IF,第i个回波分量经解调后将成为一个恒定信号,其能量将在频域内积累为一个脉冲[10]。然而,对于那些IF与模型不匹配的其他回波分量,它们的能量就不会在频域内收敛[11-12]。通过调整模型参数集,直到第i个回波分量能量最大收敛,如果将最合适的参数集表示为Zm,则目标IF 可以估计为f(T,Zm)[13]。
传统的Hough变换通常采用简单的线性模型来拟合目标IF。线性拟合模型可以表示为
式中m和n分别是线性模型的斜率和初始频率参数。
但是实际回波分量的IF 曲线通常具有非线性的特性,这导致线性模型的拟合精度不高,尤其是在曲线两端及中点部分线性拟合的结果与目标的多普勒频率之间存在很大的误差。
3 改进的穿墙雷达目标定位算法
3.1 基于经典贝塞尔拟合模型的目标定位算法
基于传统线性模型Hough变换的频率拟合算法所存在的非线性频率曲线拟合难题,一些学者提出了用非线性模型来代替传统线性模型,比如圆弧模型、椭圆模型[14]。非线性模型的使用能够补偿线性模型的非线性误差,提高多普勒频率曲线的拟合精度。但由于圆弧、椭圆的形状是相对固定的,曲率无法任意调整,很难适应复杂多变的多普勒瞬时频率曲线的拟合从而影响定位精度。因此本文提出了一种改进的目标瞬时频率拟合模型,采用能够自适应得改变曲率的自由曲线代替传统拟合模型,从而大大提高了目标定位精度。
用Qi(i=0,1,…n)来表示n次贝塞尔曲线的n+1 个控制顶点,用Bi,n(u)表示n个Bernstein 基函数中的第i个[15-16]。n次经典贝塞尔曲线可以表示为
我们提出可以用一个二次经典贝塞尔拟合模型来估计大惯量低速目标的IF,对传统的线性模型进行改进。二次经典贝塞尔拟合模型可以表示为
式中Q0和Q2分别是曲线的起点与终点,Q1是控制点,通过改变这三个控制顶点可以改变曲线的形状。当雷达系统接收到回波信号时,利用STFT 对回波信号进行时频分析,并从时频图中提取出时频点上的峰值,得到对应的时频位置,从而可以初步得到目标回波的IF 曲线。将得到的IF 曲线的端点作为贝塞尔曲线的两端的端点。然后利用基于传统的线性模型的Hough 变换在IF 曲线端点附近拟合。将拟合出的直线模型进行连接得到一个交点,最后,再连接两个端点得到一条连接线,过上述两条拟合线的交点平行于连接线作直线,在直线上搜索控制点。因此,所提出算法的计算复杂度仍为O(n)。采用二次经典贝塞尔拟合模型来代替传统频率拟合模型,能够提升拟合精度。
但是二阶贝塞尔曲线只有一个控制点,当信号能量最大化时,确定控制点,在用于拟合的过程中对目标曲线的对称性要求较高。此外,控制点确定时,二次经典贝塞尔曲线的形状将唯一确定。当需要进一步调整曲线形状时,只能重新调整控制点,这将使计算十分复杂[17]。
3.2 基于扩展贝塞尔拟合模型的目标定位算法
为了解决非对称性问题,并且在不改变控制点的情况下,根据目标的实际频率进一步调整曲线形状,使得拟合曲线能够进一步在控制点左右不同程度地逼近实际曲线,我们又提出了改进的基于扩展贝塞尔模型的目标瞬时频率估计方法。
首先,为了在不改变控制顶点的情况下构造扩展贝塞尔曲线,提高了n次贝塞尔曲线的阶数,得到如下公式
扩展贝塞尔曲线是通过改变上述公式中控制点的线性组合系数来定义的。当n为偶数时,引入n个参数,可表示为
扩展贝塞尔曲线可以用控制顶点和含参函数的线性组合表示。当n是偶数时,扩展贝塞尔曲线Pn(u)表示为
当n=2时,二次扩展贝塞尔拟合模型表示如下
式中Q0、Q2和Q1分别是由经典贝塞尔模型确定的端点和控制点。N2,i(u) (i=0,1,2)是二次扩展贝塞尔模型含参数的调配函数,可以表示为
式中,u∈[0,1],参数λ1,λ2∈[-2,1]。为了简化拟合,可将二次扩展贝塞尔曲线表示为
式(18)中的Xi,Yi(i=0,1,2)分别表示经典贝塞尔模型端点Q0、Q2和控制点Q1所对应的横纵坐标。由于二次扩展贝塞尔曲线中有两个参数λ1和λ2,其值范围为-2到1。如果使用传统枚举算法同时搜索两个参数,计算复杂度将为O(n2),这将影响检测的运算速度和实时性。通过式(17)可以发现,两个参数λ1和λ2分别调控拟合曲线与控制边Q0Q1和Q1Q2的逼近程度,两个参数在模型的调整中具有部分独立性。因此,为了避免高维参数自由搜索的过程,本文提出了一种改进的线性参数搜索算法,用线性搜索代替多维搜索。首先,假设λ1为零,然后在-2 到1 的范围内调整λ2。当信号能量集中到最大程度时,确定λ2的值。接下来,在-2 到1 的范围内搜索参数λ1。基于扩展贝塞尔的频率拟合模型能够有效解决目标多普勒瞬时频率曲线的非线性和不对称性带来的问题。
为了更加直观清晰地反映基于扩展贝塞尔模型的霍夫变换的多普勒穿墙雷达定位方法,提出算法的流程图如图2所示。
为了直观地反映线性模型、二次经典贝塞尔拟合模型和二次扩展贝塞尔拟合模型的创建,截取一段目标瞬时频率曲线。实验中,目标运动路径如图3(a)所示,接收机Rx1 为定位坐标原点,发射机Tx和接收机Rx1、Rx2在同一水平线上,并设置为X轴,以垂直接收机Rx1的方向设为Y轴。双频连续波的载波频率为2.4 GHz 和2.39 GHz,发射机与接收机距离为6.25 cm。目标瞬时频率曲线从0 s到5.12 s生成。三种模型最终拟合结果如图4(a)、(b)所示。实线代表实际的目标瞬时频率曲线,不同形状标记的线分别表示不同的频率拟合模型。
对比图4(c)、(d),我们发现这两个参数在模型的调整中具有相对独立性。当λ2=0 固定时,将λ1的值分别调整为-0.7、-0.3和0.5,得到三条不同的扩展贝塞尔拟合曲线,如图4(c)所示。可以看出,扩展贝塞尔曲线正在逼近扩展贝塞尔控制多边形的控制边Q0Q1。当λ1=0 固定时,将λ2的值分别调整为-0.7、-0.3和0.5,得到三条不同的扩展贝塞尔拟合曲线,如图4(d)所示。可以看出,此时拟合曲线正逐渐接近控制边Q1Q2。因此,两个参数在模型的调整中有相对独立性,确定两个参数的过程中用线性搜索代替多维搜索是十分有效的改进。
两种参数搜索方法对比实验结果见表1,结果表明依据两个参数之间相对独立的特性,采用线性搜索来代替传统的多维搜索,在目标定位精度相差不大的情况下,大大降低了运算复杂度,缩短运算时间,优化目标探测的实时性。
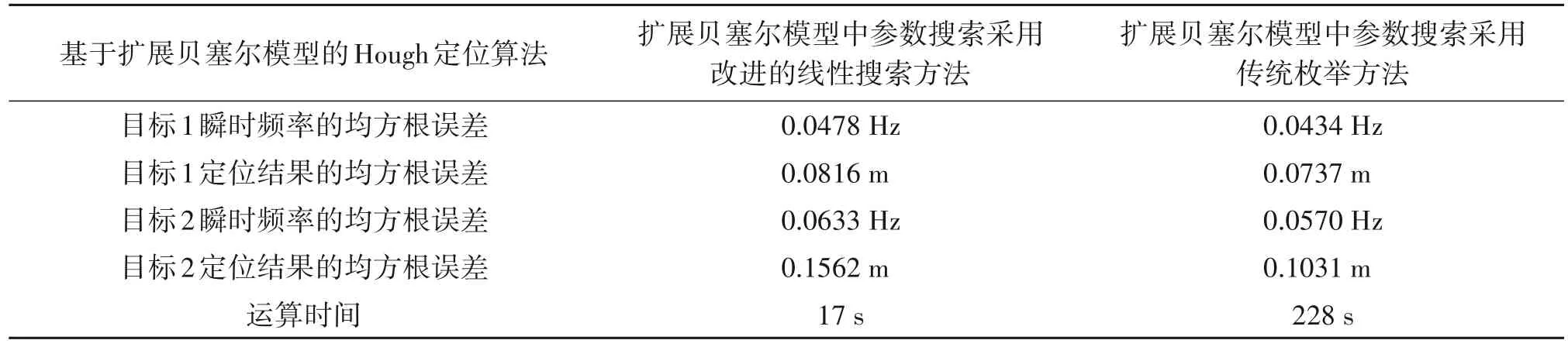
表1 目标瞬时频率估计结果和定位结果的均方根误差Tab.1 Root mean square error of target instantaneous frequency estimation result and location result
4 实验结果及分析
4.1 实验场景设置
为了验证所提出的算法的性能,进行了一系列实验。连续波穿墙雷达结构和探测场景的原型如图5。由于在实际的探测应用中,对目标的空间位置所需的要求较小,且高度波达角和方位波达角的估计原理具有相似性。因此,目标探测中,在不失一般性地情况下,本实验只估计人体目标的水平波达角和距离。对于目标在二维坐标上定位,设置接收机Rx1为定位坐标原点,发射机Tx和接收机Rx1、Rx2 在同一水平线上,并设置该水平线为X轴,以垂直接收机Rx1 的方向设为Y轴。本文的实验中,双频连续波的载波频率为2.4 GHz 和2.39 GHz,发射机与接收机距离为6.25 cm。目标1以1 m/s的横向初始速度和0.25 m/s2的径向加速度从其初始位置(2,2)移动。同时,目标2的初始位置为(2,1),初始速度为2 m/s,沿Y轴方向径向加速度为0.2 m/s2,横向加速度为0.1 m/s2,沿远离雷达阵列方向移动。两个目标的运动路径如图3(b)所示,整个实验持续约5 s。
4.2 目标定位实验结果及分析
使用基于扩展贝塞尔模型的霍夫变换的多普勒穿墙雷达定位算法的结果与传统STFT 算法、线性模型、二次经典贝塞尔拟合模型的对比见图6。图6(a)、(c)、(e)和(g)分别表示频率拟合的结果,图6(b)、(d)、(f)和(h)分别表示目标定位算法合成的运动轨迹结果。与传统STFT 定位算法相比,三种拟合模型均能有效抑制频率模糊。但线性模型无法拟合非线性明显的曲线,具有很大的局限性。二次贝塞尔模型解决了非线性这一问题,但对拟合曲线的对称性要求很高,无法满足人体目标复杂多变的运动情景。因此,扩展贝塞尔拟合模型改进算法具有很大的优越性。
实验结果表明,本文提出的扩展贝塞尔拟合模型改进算法通过引入两个形状参数,并线性搜索、动态调整两个参数,使得扩展贝塞尔拟合模型能够根据实际目标瞬时频率进行自适应调整,在经典贝塞尔模型的基础上在控制点左右不同程度地逼近实际目标瞬时频率曲线。不仅有效避免了不同目标间具有足够接近甚至重叠的瞬时频率时出现的“频率模糊”效应,还解决了目标瞬时频率曲线非线性、非对称性的拟合难题,相对于传统拟合模型大大提高了目标瞬时频率的估计精度,从而对目标的位置信息进行更精确的实时估测。
四种定位算法的结果误差对比见表2,与STFT算法相比,频率估计精度平均提高0.33 Hz,多目标定位精度平均提高0.4 m;与传统线性模型相比,频率估计精度平均提高0.10 Hz,多目标定位精度平均提高0.39 m;与无参数的经典贝塞尔模型的霍夫变换相比,频率估计精度平均提高0.03 Hz,多目标定位精度平均提高0.22 m。可以看出,基于改进Hough变换频率拟合技术的目标定位算法具有很高效的定位性能。

表2 STFT、线性模型、二次经典贝塞尔模型、二次扩展贝塞尔模型算法误差对比Tab.2 Algorithm error comparison of STFT,linear model,quadratic classical Bezier model and quadratic extended Bezier model
5 结论
本文提出了一种基于改进Hough变换频率拟合技术的目标定位算法,采用基于扩展贝塞尔模型的Hough变换频率拟合模型对多目标定位时的频率模糊区域进行瞬时频率估计。通过引入形状参数来构造扩展贝塞尔曲线,并且依据两个参数之间相对独立的特性,用线性搜索代替传统多维搜索、动态调整两个参数,利用拟合的曲线解调回波信号完成对多个目标分量的分离,并结合多普勒处理方法合成目标运动轨迹,实现对目标的实时定位。仿真结果表明,该算法不仅有效地解决了双人体目标多普勒穿墙雷达定位中的频率模糊问题,在频率估计精度上优于传统的线性模型和经典的贝塞尔模型,有效地解决了目标频率曲线的非线性和不对称性带来的问题,进一步提高了目标运动轨迹复杂多变时的适用性,具有很高的实用价值。

