基于轮胎半径自适应的智能车辆组合定位

余卓平，高乐天，夏 新，陆逸适

（1.同济大学汽车学院，上海 201804；2.同济大学新能源汽车工程中心，上海 201804；3.同济大学南昌汽车创新研究院，江西南昌 330013；4.加州大学洛杉矶分校土木与环境工程学院，洛杉矶 90095）

电动化与智能化是近年来车辆领域的两大前沿主题，其中智能化不但对车辆节能减排具有重要意义，也能极大提高交通效率和交通安全性[1］，因此已成为国内外的研究热点。对于智能汽车而言，环境感知系统尤为重要。智能汽车对周围环境的感知以及对自身状态的认知是其自主行驶的基础。车辆定位技术是智能汽车环境感知系统的关键技术之一，但由于环境复杂性、传感器成本等原因，智能车辆高精度定位问题还未得到解决。

近年来国内外针对智能车辆的定位技术已有了大量的研究，车辆定位系统可以分为2类，自主式定位系统和协作式定位系统。其中自主式定位系统是指仅依靠本车自身传感器，如GNSS（Global Navigation Satellites System）、IMU（inertial measurement unit）、轮速传感器、磁力计、摄像头和地图、激光雷达等，进行车辆定位。协作式定位系统指基于V2X（Vehicle to Everything）技术，本车与路侧单元、他车等其他交通参与者进行通讯、进行位置估计。然而目前为止还没有通用统一的V2X标准，无法保证车辆可以实时与车外设备进行通讯，因此仅依靠自身传感器的纯自主式定位系统是必需的[2］。在自主式定位系统中，GNSS、激光雷达与摄像头都易受到外界环境的影响[3］，可靠性无法保证，而IMU、轮速传感器、方向盘转角传感器等车载传感器不受外界影响，因此以INS为基础的基于多源信息融合的组合定位系统是智能车辆获取自身位置的可靠信息源。

INS系统具有自主定位的能力，通过对IMU信息进行解算，可以获取三维位置、速度及姿态信息，然而低成本MEMS（Micro-Electro-Mechanical System）惯性传感器仍具有明显的测量误差，在不经过外部信息源修正的情况下约半分钟的运算便会造成10多米的定位误差[4］。因此，很多学者利用GNSS测量反馈，提高INS定位系统的精度。Godha等[5］利用轮速获取纵向车速，利用轮速差估计航向角，通过扩展卡尔曼滤波融合了GNSS信息。Giseo等[6］基于车辆运动学模型对车速和航向角建立非线性观测器，并利用自适应卡尔曼滤波算法融合GNSS信息，得到了较好的定位精度。

当GNSS信号受干扰或受阻时，轮速传感器便是唯一可以反馈车速的信息源，增加轮速传感器可以让整个系统的性能提高68%以上[7］，因此对于智能车辆来说，轮速是定位系统重要的传感器信息之一。Li等[8］利用轮速传感器获取车辆纵向车速，基于车辆动力学模型设计了滑模观测器对车辆侧向速度进行估计，从而抑制INS系统的发散。然而要通过轮速获取车速还需要知道准确的轮胎有效滚动半径，目前大多数学者在利用轮速进行定位算法设计时均假设轮胎半径为定值，而实际上轮胎有效滚动半径为缓变量，需要考虑其变化。文献[9］通过4个车轮的轮速测量和转向识别计算补偿系数对有误差的轮胎半径值进行补偿，然而无法获得准确的轮胎半径。也有一些学者将轮胎滚动半径的变化建模成轮速传感器的刻度因数误差，然后将刻度因数扩展为一个状态利用卡尔曼滤波算法进行估计[10］。文献[11］将轮速刻度因数建模为缓变量，然后利用误差状态扩展卡尔曼滤波将GNSS、IMU、轮速传感器以及 视 觉 SLAM（simultaneous localization and mapping）信息融合进行定位。文献[12］在文献[13］建立的GNSS/INS/里程计组合定位系统的基础上，在卡尔曼滤波的状态中加入了里程计刻度因数误差并对其进行估计。

由以上分析可见，目前将轮速引入位置估计系统的研究中，绝大多数都假设轮胎半径为定值，然而由于车辆使用环境、时间的差异，载荷、温度、胎压等环境因素的变化都会造成轮胎半径产生变化[14］，从而直接影响车速的准确性，且速度越高误差越大，导致位置估计产生误差。而将轮胎刻度因数加以考虑的研究并没有考虑车轮动态，另一方面，关于轮胎有效滚动半径的研究大多是基于车辆动力学模型，利用动力学关系对有效滚动半径进行估计需要多种动力学参数信息，其获取难度大，且动力学模型具有强非线性的特点。而智能车拥有GNSS测量得到的车速信息，因此本文在GNSS信号较好时利用速度反馈，提出考虑车辆行驶动态的多模型融合轮胎有效滚动半径在线估计方法，当GNSS信号较差或不可用时，利用已更新的轮胎有效滚动半径和轮速信息获取准确车速，基于误差状态自适应卡尔曼滤波设计组合定位架构，提高组合定位系统的定位精度。

1 算法架构

本文提出了分工况多模型融合轮胎半径自适应方法，可以准确估计车轮有效滚动半径，从而有助于在GNSS信号受阻或丢失条件下得到更为精确的车辆位置估计结果。所提出的基于轮胎半径自适应的GNSS/IMU/WSS组合定位算法架构如图1所示。图中，ωRL为左侧后轮的轮速测量值；ωRR为右侧后轮的轮速测量值；vG为GNSS测量的车速；r为轮胎半径估计模块得到的轮胎有效滚动半径；vI为INS系统输出的东向和北向速度矩阵；p表示位置信息；ε表示姿态信息；Λ表示航向信息；δv、δp、δε分别表示卡尔曼滤波输出的速度、位置和姿态误差。

图1 算法架构Fig.1 Structure of algorithm

首先，在GNSS信号良好时，通过GNSS的速度测量以及由车辆CAN总线采集到的轮速信号对非驱动轮有效滚动半径进行在线估计。在进行轮胎半径自适应估计算法设计时，考虑车辆行驶工况，根据车辆动态变化情况基于卡尔曼滤波对车轮半径进行多模型估计，通过估计结果的融合得到当前车轮有效滚动半径。

车辆定位模块基于惯性导航系统进行位置输出。惯性导航系统根据IMU测量得到的三轴加速度及角速度信号得到车辆的速度、姿态及位置信息。当GNSS信号良好时，使用双天线GNSS接收机得到的位置信息、航向信息及由轮速信号和轮胎半径得到的车速信息，然后利用状态误差自适应卡尔曼滤波对多源信息进行融合得到车辆位置及航向信息。当GNSS信号较差或消失时，将由轮速和轮胎半径计算得到的车速作为测量信息，对INS系统的输出进行校正，最终得到车辆的位置信息。

2 自适应卡尔曼滤波

2.1 卡尔曼滤波

根据轮胎半径自适应系统模型和INS系统模型特点，选用卡尔曼滤波算法进行信息融合。本文的轮胎半径自适应模块采用了双状态卡尔曼滤波器，而组合定位模块采用了15状态的误差状态卡尔曼滤波器。一般的离散状态卡尔曼滤波状态方程可表示为

式中：X为状态；w为过程噪声矩阵；Φ为状态转移矩阵；下标k表示第k时刻。测量方程可表示为

式中：Z为测量量；H为观测矩阵；η为测量噪声矩阵。

2.2 卡尔曼滤波自适应方法

对于线性系统，卡尔曼滤波获得较好效果的前提是系统模型和噪声特性精确已知，而实际中过程噪声Q和测量噪声R的不确定性会显著降低滤波效果。传统的卡尔曼滤波中Q和R矩阵都是根据经验选取为定值，然而在实际应用中，噪声特性可能时刻变化，这一假设并不成立，因此最有效的方法是对噪声矩阵进行自适应。本文使用的自适应卡尔曼滤波方法[15］定义了比例系数α，表示为

其表征了卡尔曼滤波过程中新息协方差和预测新息协方差的粗略比例。式中，trace为矩阵的迹；P̂k-1为k-1时刻的协方差矩阵预测值；Qk-1为k-1时刻的过程噪声矩阵；Q̂k-1为k-1时刻的过程噪声矩阵预测值。由此，自适应规则设计为

该卡尔曼滤波自适应方法可以有效提高算法的精度和鲁棒性。

3 轮胎有效滚动半径自适应算法设计

GNSS速度测量和轮速测量都可表征车速，相比GNSS速度，轮速信号具有采样频率高、信号稳定平滑的特点，而GNSS信号易受环境影响，如城市环境下GNSS信号的多路径效应，隧道、树木等遮挡条件下GNSS信号易丢失，因此对于车辆组合定位系统来说，轮速比GNSS速度测量更加稳定。然而由轮速得到车速还需经过轮胎有效滚动半径的转换，因此准确的轮胎有效滚动半径对于车速的准确获取具有重要意义。由于轮胎的滚动半径是缓变量，因此可以在GNSS信号有效时对轮胎半径进行在线估计，当GNSS受阻或信号较差时，使用更新过的轮胎半径得到准确车速，以提高组合定位系统的精度。

轮胎有效滚动半径估计系统如图2所示，分为轮加速度估计系统、轮胎半径估计系统一、轮胎半径估计系统二、轮胎半径融合共4个子模块。选取车辆非驱动轮的轮速信号作为测量信号，轮速取左右两侧车轮轮速的均值，即

图2 轮胎有效滚动半径自适应系统框图Fig.2 Structure of tire radius adaption system

式中：ω为轮速均值，即本文用于算法的轮速。

3.1 轮胎半径估计系统一

假设相邻两采样时刻车轮角加速度为零，即ω̇=0，则选取卡尔曼滤波状态量为X1=[vk rk]T，轮胎半径估计系统离散模型可表示为

式中：v为车速；r为轮胎半径。根据GNSS测量得到的车速，测量方程为

利用自适应卡尔曼滤波可以得到估计系统一的轮胎有效滚动半径估计值r1。

3.2 轮加速度估计系统

基于轮加速度为零的假设，轮胎半径估计系统一在大多数正常行驶情况下均可以得到平滑准确的轮胎有效滚动半径估计值。然而，当车辆进行急加速、急减速等大动态运动时，轮加速度为零的假设不再成立，轮胎半径估计结果精度下降，无法满足精度和平稳性要求，因此在大动态情况下，需考虑轮加速度对系统模型精度带来的影响。

由于轮速测量噪声影响，轮速信号不可直接求导计算轮加速度，使用卡尔曼滤波对噪声进行处理。选取状态量为X2=[ωω̇]T，轮加速度估计系统离散模型为

式中：ω̇为轮加速度；ΔT为采样间隔。测量量为轮速，测量方程为

利用自适应卡尔曼滤波算法估计轮加速度。

3.3 轮胎半径估计系统二

当车辆动态较强时，将轮加速度考虑进轮胎半径估计系统模型，选取状态量为X3=[vk rk]T，系统方程可表示为

测量量为GNSS反馈的车速，测量方程为

利用自适应卡尔曼滤波方法可以得到估计系统二的轮胎有效滚动半径估计值r2。

3.4 轮胎半径估计值融合

虽然考虑轮加速度的轮胎半径估计系统可以在车辆具有较大动态时得到较好的估计结果，但在一般正常行驶工况下，轮加速度估计误差会给系统方程带来误差，反而会造成估计结果抖动，因此，需要根据车轮动态对2个轮胎半径估计系统的输出值进行融合。设计如下的融合策略：

式中：ω̇high、ω̇low分别为轮加速度上、下阈值，具体取值需根据经验及试验数据进行选取，本文选取的轮加速度上阈值为4rad·s-2，下阈值为2rad·s-2。该融合策略可以保证在车轮低动态时采用估计系统一的轮胎有效滚动半径估计值，在车轮动态较强时选取估计系统二的输出值，而轮加速度在二者之间时对2个系统的输出值进行加权融合，保证估计结果的连续和稳定。

4 GNSS/IMU/WSS组合定位系统

4.1 状态方程

选取位置误差、速度误差、姿态误差、加速度计和角速度计误差共15维状态向量[16］作为状态误差自适应卡尔曼滤波的状态量，即

4.2 测量方程

根据轮胎半径自适应结果可以得到足够准确的车速，因此此时根据轮速测量值和INS系统输出的航向可以得到车辆在当地坐标系下的东向和北向速度。

式中：ve，ω、vn，ω分别表示由轮速换算得到的车辆东向和北向速度。

（1）当GNSS信号质量良好时。此时GNSS可以为组合定位系统提供位置、速度及航向测量。其中，位置、航向测量用于INS系统的状态误差自适应卡尔曼滤波，而速度测量用于更新轮胎有效滚动半径，经轮速和航向换算后的东向、北向速度作为卡尔曼滤波的测量。因此，系统测量为

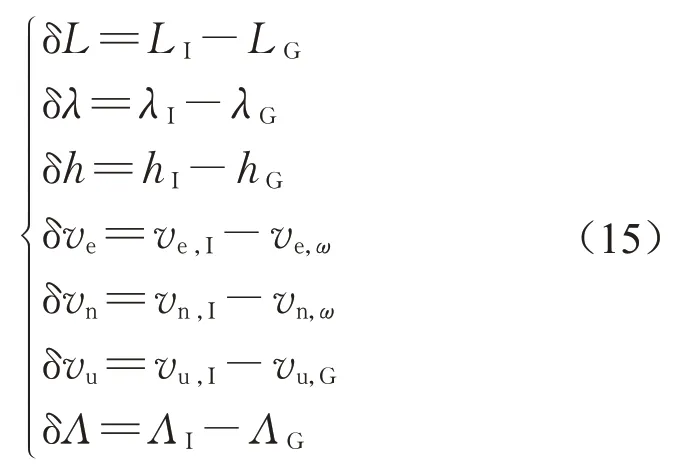
式中：下标I，G分别表示INS系统的输出值和GNSS的测量值。

（2）当GNSS信号受阻时。此时GNSS测量信息不可用，因此系统测量为

利用自适应卡尔曼滤波方法可以得到最终的车辆位置估计结果。

5 试验验证

5.1 试验条件

试验车辆为某型号前轮驱动电动汽车，如图3所示。试验在如图4所示的道路环境下进行，从图中三角符号位置出发，到正方形符号位置结束，整个试验持续约630s。选取2种代表性工况进行分析。在图4中圈1部分检验GNSS信号良好状态下轮胎半径自适应效果；在圈2部分人为制造GNSS丢失，以检验组合定位算法效果。

图3 试验车Fig.3 Test vehicle

图4 试验路径和环境Fig.4 Trajectory and test environment

系统硬件结构如图5所示，IMU传感器为ADIS16490，输出三轴加速度及三轴角速度信号；轮速信号由车辆OBD接口采集；GNSS板卡为Trimble BD982，用于测量车辆速度和位置，选用双天线GNSS，用于测量车辆航向。所有信号都接入CAN总线，由NI CompactRIO 9082数采设备采集。

图5 系统硬件结构图Fig.5 Topology of hardware system

5.2 轮加速度估计算法验证

轮加速度估计效果如图6所示，由图可以看出，若对轮速信号直接进行求导，由于噪声等因素的影响，对原信号的噪声具有放大效应，所得到的结果剧烈抖动，无法满足算法要求。采用本文所提出的轮加速度估计算法，可以得到平滑准确的估计值，有效过滤了噪声的影响。

图6 轮加速度估计效果Fig.6 Results of wheel acceleration estimation

5.3 轮胎有效滚动半径估计算法验证

根据文献[11］，由于胎压、温度、载荷等外界影响，轮胎半径的变化一般可以达到0.5cm左右。通过Kistler Smotion光学速度传感器测量数据和轮速传感器测量值通过数据拟合可以得出，本文所采用的车辆轮胎半径标准值为0.26m。试验时设置轮胎半径初值为0.255m，以模拟由于胎压、磨损等情况造成的轮胎有效滚动半径波动。由于在GNSS效果良好时，轮胎半径估计效果类似，选取305～325s时间段的数据进行分析，如图7所示。由图7a可以看出，融合后的轮胎半径估计值整体在估计系统一和估计系统二的输出值之间，当车轮低动态时，轮加速度对估计模型的影响较小，此时若将轮加速度引入系统，估计误差反而会造成估计结果抖动，因此采用估计系统一的轮胎有效滚动半径估计值；在车轮动态较强时，轮加速度对系统影响明显，因此考虑车轮动态，选取估计系统二的输出值，最终进行模型融合得到了更为平稳的估计值。

图7 轮胎半径估计结果Fig.7 Estimation results of tire radius

为了更清晰地展现算法的效果，将313～316s的数据放大，如图7b所示。在从313s到315s的试验过程中，轮加速度由较大值变化到较小值（对应轮加速度可参考图6），在最初阶段，融合估计的结果也相应使用了估计系统二的结果，可以看出将轮胎动态考虑进系统方程得到了更接近真实值且更稳定的估计结果。而轮胎动态变弱之后，可以看出估计系统二的估计结果已偏离了均值线，出现了明显偏差，此时融合估计器选取了估计系统一的结果，保证了估计精度。在2种估计效果进行切换的过程中，融合估计器的加权取值方法保证了估计结果的平稳性。

将305～325s的估计结果进行统计，结果如表1所示。可以看出，融合估计系统的输出值具有最小的方差，相比不考虑车轮动态的估计系统一的结果提升了6.4%；相比考虑车轮动态的估计系统二的结果提升了20.7%。

表1 轮胎半径估计结果对比Tab.1 Results comparation of tire radius estimation

5.4 GNSS/IMU/WSS组合定位算法验证

在图5所示的试验路径图中，在进入圈2所示区域时将INS系统的GNSS信号输入切断，验证在无位置反馈条件下基于轮胎半径自适应的组合定位系统的定位精度。而GNSS采集得到的位置仅作为定位真值进行对比。当GNSS信号切断时，对比经过自适应具有准确轮胎半径的组合定位系统和选用不准确的轮胎半径初值的组合定位系统的定位结果，试验结果如图8所示。

以GNSS获取的定位结果为真值，则由图8可以看出，使用不够准确的初始轮胎半径的定位结果较差，这是由于不准确的轮胎半径会造成车速计算产生误差，从而直接转换为位置误差，且由于没有GNSS的位置反馈修正，位置误差会随着时间增长一直累积。而当使用轮胎半径自适应系统对轮胎半径进行提前纠正后，虽然无法完全消除累积误差，但定位误差显著变小，经度误差和纬度误差见图9，在GNSS信号丢失40s的条件下，若采用轮胎半径自适应的定位算法，经度定位精度提高了34.9%，且纬度误差降低了30.7%。因此可以看出，所提出的基于轮胎半径自适应的组合定位方法可以有效提高智能车辆在GNSS丢失条件下的定位精度。

图8 轮胎半径不同时定位结果对比Fig.8 Results of vehicle localization at different tire radius

图9 定位误差Fig.9 Localization error

6 结语

智能车辆的组合定位系统中不准确的速度反馈会直接影响INS系统性能，而利用轮速获取车速时必须要有准确的轮胎有效滚动半径，因此本文考虑车辆动态，提出了基于多模型融合的轮胎有效滚动半径估计系统，在GNSS信号良好时对轮胎半径进行自适应，以在GNSS丢失条件下获取准确车速，从而提高位置估计的精度。通过研究发现，考虑车轮动态可以有效提高轮胎半径估计系统的鲁棒性，得到更加平滑的估计结果，准确的轮胎有效滚动半径可以有效提高GNSS丢失条件下的定位精度。本文所提出的轮胎半径估计结果也可以应用于智能车辆需要利用轮速计算车速的其他控制系统中，如稳定性控制等，具有一定的实用性。

作者贡献声明：

余卓平：研究思路指导、资源获取。

高乐天：算法设计及调试、试验数据分析、论文撰写。

夏 新：算法调试、试验数据获取。

陆逸适：算法调试、试验平台搭建。