饱和多孔介质渗流的强-弱不连续统一非局部模型

孙宇麒，禹海涛

（1.同济大学土木工程学院，上海 200092；2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都 610059；3.同济大学土木工程防灾国家重点实验室，上海 200092）

岩土体是含有孔隙和裂隙的非均匀多孔介质，这类多孔介质中流体传输过程需要穿越由介质中孔隙、裂隙和物质界面组成的强-弱不连续面，这与经典连续介质力学模型中描述局部流体模型的偏微分方程是不相容的，从而导致需要额外的数值技术来描述流体在这些不连续界面的力学行为[1-3］。

目前兴起的近场动力学（Peridynamics）理论为该问题分析提供了一种新的思路。近场动力学是由Silling等[4-5］提出的一种新的非局部理论，其控制方程是积分方程，考虑连续体内物质点之间非局部相互作用，避免了经典连续介质模型中偏微分方程带来的空间求导奇异性[6-7］。目前近场动力学已经被广泛应用于包括脆性材料断裂[8-9］、黏弹性断裂[10-11］和多物理场耦合断裂[12］等各类非连续问题。将原本描述断裂等不连续问题的近场动力学理论应用于饱和多孔介质流体传输问题，其关键在于如何建立多孔介质中流体传输的非局部形式守恒律方程和本构律方程。

近期已有一些学者通过修改近场动力学方程以建立孔隙介质中流体传输的控制方程，如Ni等[13］和Bobaru等[14］首先将键型近场动力学模型中能量对应的思想扩展到热传导和流体传输问题，建立了热-流耦合的非局部模型；同样地，Oterkus等[15］也建立了一种热-流耦合的非局部键型近场动力学模型；随后Katiyar等[16-17］基于常规态型近场动力学模型推导出多孔介质中流体传输的非局部形式控制方程，并研究了流体穿越介质中不连续界面的力学行为。然而，上述研究主要针对键型和常规态型近场动力学模型，由于物质点之间键的相互作用是独立的，从而导致其推导的非局部扩散模型无法描述流体传输的非线性力学行为。此外，目前所发展的非局部传输模型主要基于键型模型中能量对应的思想，与经典连续介质力学模型之间的对应关系不够清晰。

基于统一变分近场动力学[18］的基本思想，本文提出一种表征饱和多孔介质中流体非局部传输作用的流量向量态函数，统一描述流体在强-弱不连续面传输过程中的力学行为，避免局部力学模型在不连续界面处出现的导数无定义性，并建立相应非局部形式的质量守恒方程、线动量守恒方程和本构方程。从理论证明了当非局部流体模型中的非局部作用半径趋于零时，该非局部模型将退化为经典连续介质力学中的Darcy流体模型。另外，提出一种基于罚函数方法的全隐式数值求解格式，旨在消除非局部模型内在的零能模式难题，保证数值结果的精确性。

1 渗流传输的非局部控制方程

1.1 非局部质量守恒方程

在传统局部模型中，水压力梯度是驱动多孔介质中流体传输的主要因素，故质量守恒方程以偏微分方程形式呈现。基于非常规态型近场动力学中的力态公式[6-7］，本文提出了流量态向量的概念，并给出了非均匀岩土介质中流体传输的非局部形式质量守恒方程。

图1为非均匀饱和多孔介质中渗流输运的非局部模型示意。

图1 非均匀饱和多孔介质中渗流输运的非局部模型示意Fig.1 Schematic of the nonlocal fluid transport model in the heterogeneous saturated porous media

假设多孔介质中流体处于恒温条件下的弱可压缩状态，流体密度和压力之间满足关系如式（1）：

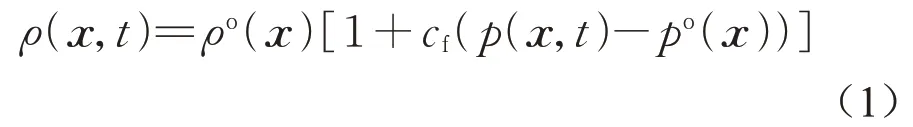
式中：ρ(x)为流体密度，kg·m-3；x为流体物质点的位置矢量，m；t为时间变量，s；ρo(x)为参考流体密度，kg·m-3；cf为流体压缩系数，Pa-1；p(x，t)为流体压力，Pa；po(x)为参考流体压力，Pa。流体传输的非局部质量守恒方程可表示为

式中：-U[x′，t]x′-x和-U[x，t]x-x′分别表示在流体物质点x′和x处的流量态矢量，kg·m-6·s-1；Hx表示流体物质点x的非局部作用区域；q(x，t)为所考虑多孔介质区域内流体源的流量函数，kg·m-3·s-1.需要说明的是，流量态矢量中x′-x和x-x′表征了流体x′和x之间的传输作用。

流体物质点之间非局部传输作用的流量态矢量定义如下：

式中：u(x，t)为流体流速，m·s-1；‖x-x‖′为x′和x之间的欧氏距离；ω(‖x′-x‖)为核函数，其定义如式（4）：

式中：x′的积分区域为x的非局部作用区域Hx。

1.2 非局部线动量守恒方程与本构方程

为了得到完整描述非均匀多孔介质中流体传输的非局部模型，还需定义流体传输的非局部线动量守恒方程和本构方程，其非局部动量守恒方程定义为

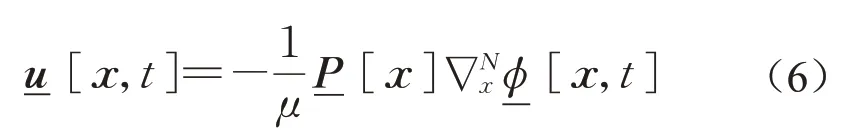
式中：μ为流体黏度；-P[x]为x处的非局部有效渗透率张量，由式（7）非局部本构方程确定。

式中：Pab为饱和岩土介质的绝对渗透率张量；kr(x)和kr(x′)分别为x′和x的相对渗透率系数。∇Nxϕ-[x，t]为流体势函数的非局部梯度，如式（8）：

式中：-ϕ[x′，t]x′-x和-ϕ[x，t]x-x′为x′和x处的非局部流体势标量态函数。

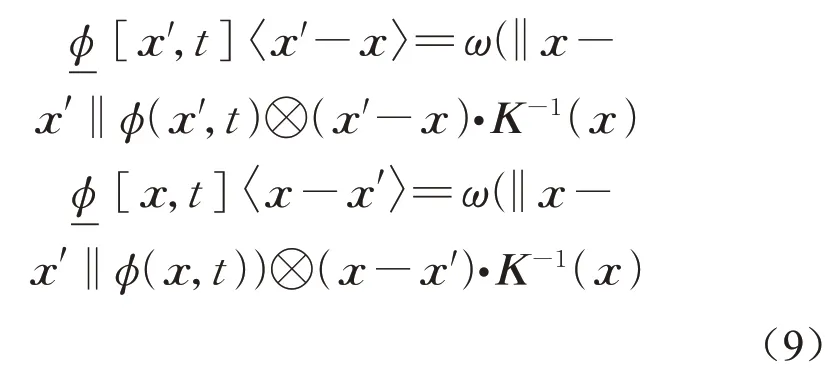
式中：ϕ(x，t)=p(x，t)-ρ(x)gz(x)为物质点位置矢量的局部势流函数，本文忽略由于重力产生的流体势函数ρ(x)gz(x)。

式（1）、式（5）和式（6）构成了非均匀饱和多孔介质中流体传输的全部控制方程，为了求解该方程，还需引入非局部压力边界Γpg和流量边界Γph，如图1所示，采用文献[16］所提出的边界施加方法。

1.3 与经典Darcy流模型的一致性证明

本文的非局部渗流模型引入非局部作用半径来表征流体物质点之间的传输作用。接着理论证明，当物质点之间的作用半径趋于零时，非局部模型退化为局部的Darcy流体模型。

基于Taylor公式，Hx中物质点处x′的局部流量

式中：∇x(ρ(x，t)u(x，t))表示x处的流量梯度；r(‖x′-x‖2)表示Taylor公式中的高阶余项。

将式（9）代入式（1） ， 得到

式中：Δ(ρu)(x′，x，t)=ρ(x′，t)u(x′，t)-ρ(x，t)u(x，t)为x′和x处流量的差值；∇x(ρ(x)u(x，t))为流量函数的局部梯度。从式（11）可知，当物质点的非局部作用区域Hx的半径δx趋于零时，非局部质量守恒方程将退化为局部质量守恒方程。由此定义流量的非局部梯度算子为

同理，对Hx中x′的势流函数ϕ(x′，t)进 行Taylor展开，可以得到

将式（12）代入式（7），可得渗流的局部线动量守恒方程和非局部质量守恒方程如式（14）：

式中：Δϕ(x′，x，t)=ϕ(x′，t)-ϕ(x，t)为x′和x处流体势函数的差值；∇xϕ(x，t)为流体势函数在x处的具体梯度。注意到x处的非局部渗透率张量和局部渗透率张量有如式（15）的关系：

结合式（13）和式（14）可知，当物质点的非局部作用半径δx趋于零时，非局部的线动量守恒方程、本构方程与局部线动量守恒方程、本构方程可通过如式（16）等式建立对应关系。

2 非局部变分框架与全隐式数值求解格式

2.1 非局部变分公式与物质点离散

不连续伽辽金方法[19-20］和物质点离散方法是高效求解非局部模型的有效数值离散方法。将待求解多孔介质区域离散为Np个物质点{xI}Np I=1，每个物质点的体积为ΔVI，则待求解的多孔介质区域Ω可用物质点表征为

xI的非局部作用区域HxI内，其物质点可用局部编号表示为

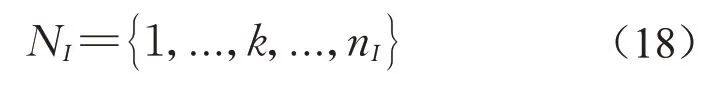
与有限元方法求解偏微分方程的离散弱形式相同，定义离散试验函数空间和离散测试函数空间如式（19）：

则非局部传输模型的离散弱形式可表示为

式中：δp=δp(x，t)为压力的变分函数；gp(xI，t)为非局部压力边界Γpg上的压力函数；hp=hp(x，t)为

式中：下标dis表示欧氏空间的离散内积；ΔVxI为xI的体积；N͂p为非局部流量边界Γph内的物质点数；

2.2 零能模态控制

由于非局部梯度（11）内在的零能模式将导致数值解答产生严重的数值震荡问题[21］，通过引入罚函数控制零能模式的出现，定义xI处的罚函数如式（23）：

式中：λi(xI)(i=1，...，nd)为物质点xI的形状张量K(xI)的特征值；α为罚函数因子，取1×10-3～1×103。zp(xJ，xI，t)为xI和xJ之间非一致部分压力变化，定义如式（25）：

对离散罚函数（22）分别求一阶和二阶变分导数，可以得到罚函数荷载向量和罚函数刚度矩阵

2.3 隐式数值求解格式

为能精确模拟流体在介质中界面、裂隙和孔隙处传输行为，在推导罚函数荷载向量和刚度矩阵的基础上，采用Newton-Raphson隐式方法进行求解[22-23］。结合式（19）和式（27），可得最终求解的非线性方程如式（29）：

式中：Δtn为时间步长；pn=[p1(tn)，p2(tn)，...，pNp(tn)]T。矩阵B和C(p)、向量f(p)的定义为

其中BI、Gp，I和DI定义为

3 模型验证

为验证本文提出的非局部流体模型在模拟不连续面上流体力学行为的精确性，采用二维高渗透差问题作为验证模型。几何模型和边界如图2所示，模型的长、宽各为0.02m，流体的黏度系数取μ=1kg·m-1·s-1。模型的渗透性分布由式（33）控制：

图2 高渗透差问题模型示意Fig.2 2D porous media with a high-contrast permeability

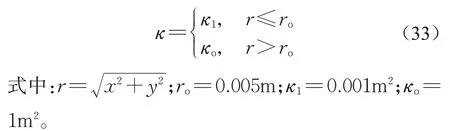
假设整个模型中存在单一流体源q(r)=

在数值计算中，物质点间距取ΔX=ΔY=2.5×10-5m，物 质 点 作 用 半 径 为罚函数因子α=5κ。图3a为非局部模型计算结果，图3b为数值计算结果与解析解误差。由图3可知，本文提出的非局部流体模型能精确捕捉流体在穿越物质界面上的不连续力学行为，同时也证明了非局部模型解空间中内蕴的不连续性，及其在模拟含不连续界面多孔介质流体传输问题上的有效性。

图3 非局部模型数值计算结果与解析解答对比Fig.3 Comparison of the numerical results of the nonlocal model with analytical solutions

4 三维含孔隙非均匀多孔介质中的流体传输模拟

由于多孔介质的非均匀性与孔隙分布特征，三维情况下流体穿越不连续界面的力学行为更加复杂，因此研究三维条件多孔介质流体传输问题有重要意义。本算例考虑长L=1m、宽W=1m、高H=1m的多孔介质，在多孔介质两侧各有一个半圆形空腔，几何模型和边界如图4所示。

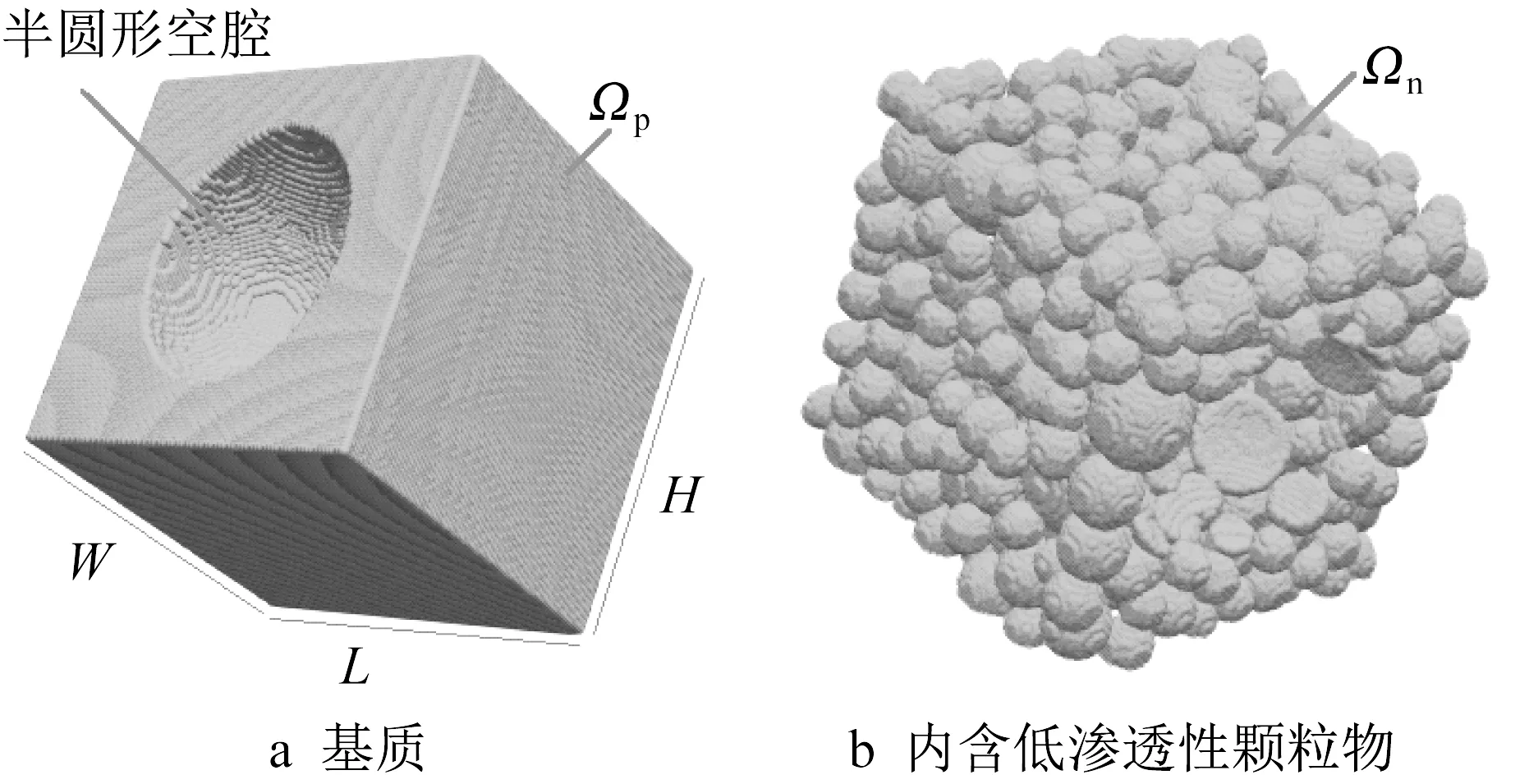
图4 含半圆形空腔三维多孔介质、多孔几何模型示意[23］Fig.4 Schematic of the geometric model for 3D porous media containing cavities[23]

流体黏度μ=2.5kg·m-1·s-1，模拟区域的孔隙度ϕ=0.55，基质渗透性为κp=1m2，并随机分布渗透性为κn=1×10-4m2的颗粒物，定义流体源分布函数为

5 结语

图5 非均匀饱和多孔介质中非局部流量和流体速度矢量场分布Fig.5 Nonlocal fluid flux and velocity field distribution in the saturated heterogeneous porous media containing two cavities at a time

基于非常规态型近场动力学模型及其变分原理创建了非均匀多孔介质流体传输模拟的强-弱不连续统一非局部模型，能有效模拟多孔介质中流体在穿越孔隙、裂隙和物质界面时的不连续力学行为，通过与解析解对比验证了模型的精确性，并基于三维复杂多孔介质中流体传输的模拟分析了多孔介质中流体传输时的不连续力学行为。得到的结论如下：

（1）基于近场动力学力态函数提出了流量态函数和相应的流体非局部控制方程，可以描述多孔介质中流体传输的非局部效应，并有效捕捉了多孔介质中强-弱不连续处流体的输运，且当物质点的非局部作用趋于零时，流体的非局部控制方程将退化为经典连续介质力学中的Darcy流体模型，从而建立了多孔介质流体传输模拟的局部模型与非局部模型之间的联系。

（2）建立的非局部流体输运方程具有与经典连续介质力学统一的变分原理，不仅适用于无网格离散，也同样适用于基于网格的数值方法，为耦合局部模型与非局部模型提供了新的耦合途径。

（3）针对非局部模型存在的零能模态问题，提出了一种罚函数方法并推导出全隐式数值方法，能有效消除非局部模型数值计算存在的数值震荡问题，精确模拟了多孔介质中流体传输的非连续力学行为，为研究流体在多孔介质中不连续界面传输的力学行为提供了理论依据。

作者贡献声明：

孙宇麒：模型构建、数据分析呈现及论文撰写。

禹海涛：项目负责人、指导模型构建及数据分析，论文修改。