基于演化博弈的重大工程项目社会责任履行决策研究
马 力, 张宇弛
(大连理工大学 建设管理系, 辽宁 大连 116024)
改革开放以来,随着社会经济的高速增长,我国重大基础设施工程项目迎来了宝贵的发展机遇,陆续建设了一批如南水北调工程、京沪高速铁路、北京冬奥会、港珠澳大桥等代表性的重大基础设施工程。“十四五”规划《纲要》确定我国将进一步推进川藏铁路、西部陆海新通道等新一批重大工程建设。然而,重大工程给我们带来巨大经济效益的同时,也经常伴随着工程腐败、生态破坏、移民安置不当、安全事故等严重的社会问题[1,2]。这些问题的根源在于利益相关者(尤其直接参与方)对重大工程社会责任的漠视[3]。重大工程社会责任(Megaproject social responsibility以下简称MSR)被概述为:“重大工程在整个项目全生命期内,各利益相关者以可持续发展为目标,通过透明、符合道德的行为,对人类社会带来影响而承担的责任”[4]。
重大工程社会责任作为提高重大工程可持续性的一项重要因素,受到广泛的关注,逐渐成为工程管理领域新的研究热点[5]。但相关研究尚处起步阶段,现有的研究主要聚焦于重大工程社会责任的内涵、关键要素、组织行为等方面,少有提及各参与方MSR履行决策问题。Zeng等[4]综述以往重大工程社会责任研究主题,提出了一个包含重大工程社会责任的多维复杂性与互动交叉性的概念模型,为重大工程社会责任的研究提供了全新思路。在此基础上,马汉阳[6]从经济、法律、伦理和政治四个维度分析了重大工程社会责任。接着Lin等[7]从内部和外部两个方面识别了重大工程社会责任的驱动因素。针对一些特殊的社会责任行为,Wang等[8]验证了重大工程参与方的环境责任认知对环境承诺和环境公民行为的正向影响,并提出了相应的环境公民行为引导策略。积极履行MSR有助于改善政府和企业形象、规避道德风险,提升社会整体效益[9]。履行MSR前期往往需要大量投资,然而对利益相关者收益的提升效果往往难以立竿见影,因此存在部分施工企业逃避履责、部分政府部门消极推动履责的情况[10]。另外,重大工程项目利益关系复杂,对于协同履责而产生的收益分配没有清晰的界限,缺少合理的利益分配机制是阻碍利益相关者履行MSR另一重要原因。为了营造良好的履行MSR环境,施工企业需要被政府部门进行监管,政府部门也需要设定合理的利益分配系数减少双方利益冲突。重大工程项目生命周期长,随着时间的推进,政府部门和施工企业会不断改变策略以获得最有利结果,因此政府部门和施工企业在履行MSR的决策过程中必然存在动态博弈,通过揭示双方博弈的演化规律,设计合理的政府监管机制、利益分配机制促进双方形成积极参与、自觉履行社会责任的格局显得尤为重要。鉴于此,本文运用演化博弈理论和SD模型仿真,尝试揭示政府不同监管力度、收益分配系数等因素对施工企业履行MSR决策的影响及其双方决策的演化机制,并为重大工程项目中政府监管、收益分配政策的制定提供参考对策。
1 演化博弈模型构建及分析
本文考虑的是重大工程项目利益相关者在社会责任履行中的策略选择问题。由于重大工程项目利益相关者较多,故选择影响相对较大的政府部门和施工企业两类博弈群体研究。重大工程对社会、经济和生态具有重大而深远影响,一旦出现社会责任风险,损失影响的范围和程度比一般工程更大,因此需要采取MSR的积极策略,但是由于主观意愿或履责成本过大等原因,也有可能会选择MSR的消极策略[11]。因此,政府部门策略集合为{推动MSR,不推动MSR},施工企业策略集合为{履行MSR,不履行MSR}。假设政府部门和施工企业不采取任何行动基础收益分别为πg,πp;政府部门推动施工企业履行MSR成本为Cg,对履行MSR的施工企业奖励J,否则给予惩罚K;施工企业履行MSR成本为Cp;公众举报的概率为p,此时若政府没有推动社会责任履行,则会受到E的声誉损失;双方单独积极行为产生的收益增量分别为Δπg,Δπp,考虑到一般工程影响小,重大工程影响较大,双方各自收益会互相影响。不同于一般工程项目,重大工程项目利益相关者多且杂,各利益相关者行为对其他参与方有很大的影响,因此本文不仅需要考虑利益相关者间的协同效应,也要考虑“搭便车”效应。设L为双方协同带来的总利润增量系数;α,β为双方收益分配系数;m,n为双方积极行为对另外一方“搭便车”的收益系数。由于协同产生的收益一定大于各自的收益和“搭便车”收益之和,因此αL(Δπg+Δπp)>Δπg+mΔπp,βL(Δπg+Δπp)>Δπp+nΔπg[12]。
根据上述说明,可得如表 1 所示的地方政府与施工企业的演化博弈收益矩阵。

表1 政府部门和施工企业动态博弈矩阵
设政府部门选择推动社会责任策略的概率为x,不推动社会责任策略的概率为1-x;施工企业选择履行MSR策略的概率为y,不履行MSR策略的概率为1-y。
基于上述博弈矩阵可以得到,政府部门选择推动社会责任履行的期望收益为
EGY=y[πg+αL(Δπg+Δπp)-Cg-J]+
(1-y)(πg+Δπg-Cg+K)
=πg+Δπg-Cg+K+yαL(Δπg+Δπp)-
J-K-Δπg
政府部门选择不推动社会责任履行的期望收益为
EGN=y[pg+mΔπp-pE]+(1-y)(πg-pE)
=πg-pE+ymΔπp
政府部门混合期望平均收益为
EG=xEGY+(1-x)=x(Δπg-Cp-K+pE)+
xy[αL(Δπg+Δπp)-Cg-J-Δπg+Cp-K-mΔπp]+ymΔπp+πg-pE
政府部门策略的复制动态方程为:
=x(1-x){Δπg-Cg+K+pE+
y[αL(Δπg+Δπp)-J-K-Δπg-mΔπp]}
类似地,可求出施工企业的复制动态方程:
=y(1-y){Δπp-Cp+x[βL(πg+πp)+
J+K-Δπp-nΔπg]}

为表达简便我们令
Δπg-Cg+K+pE=Λ1,Δπp-Cp=Λ2,
βL(Δπg+Δπp)+J+K-Δπp-nΔπg=Λ3,
αL(Δπg+Δπp)-J-K-Δπg-mΔπp=Λ4,
则动态系统雅克比矩阵为:
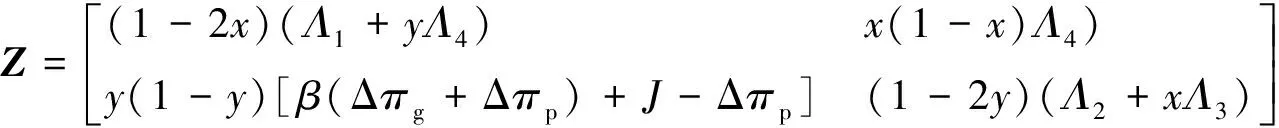
由演化博弈模型中均衡点判定的方法可知,如果雅可比矩阵的行列式符号为正,迹的符号为负,则表明相应的均衡点是稳定点[13]。五个均衡点所对应雅克比矩阵的行列式与迹如表2所示。
由上述假设βL(Δπg+Δπp)>Δπp+nΔπg,因此Λ3>0,在其他参数大小不确定的情况下,本文将探讨不同参数条件下各均衡点的情况,分析结果如表3所示。

表2 各均衡点雅克比矩阵Det(Z)、Tr(Z)取值

表3 不同参数取值范围下各均衡点的稳定性分析结果
由于情况较多,并且我们最终是想要达到政府部门推动,施工企业履行社会责任这一理想状态,所以选择演化稳定点为(1,1)的情形进行分析。
(1)当政府单独推行社会责任、给予施工企业的惩罚与声誉惩罚的和Δπg+K+pE大于政府推行社会责任付出的成本Cg,施工企业单独行动获得的利益增量Δπp大于付出的成本Cp,政府部门和施工企业合作下,若政府部门获得的利益溢出量αL(Δπg+Δπp)-Δπg-mΔπp大于给予施工企业的惩罚和奖励的和K+J,即Λ1>0,Λ2>0,且Λ4>0时,满足情形1,策略将会向政府推动、施工企业履行演化,如图1。
(2)当政府部门获得的利益增量与声誉惩罚的和αL(Δπg+Δπp)+pE大于政府部门给予施工企业的惩罚、搭便车获得的收益和推行社会责任成本的和Cg+mΔπp+J,即Λ1>0,Λ2>0,Λ4<0,Λ1+Λ4>0时满足情形3,与图1情况相同。

图1 情形1、情形3
(3)当政府单独推行社会责任、给予施工企业的惩罚与声誉惩罚的和πg+K+pE大于政府部门推行社会责任付出的成本Cg,政府部门获得的利益溢出量αL(Δπg+Δπp)-Δπg-mΔπp小于给予施工企业的惩罚和奖励的和K+J,政府部门和施工企业合作下,若施工企业合作收益与奖惩和βL(Δπg+Δπp)+J+K大于搭便车利润与履行社会责任成本的和nΔπg+Cp,当政府部门获得的利益增量与声誉惩罚的和αL(Δπg+Δπp)+pE大于政府部门给予施工企业的惩罚、搭便车获得的收益和推行社会责任成本的和Cg+mΔπp+J时,即Λ1>0,Λ2<0,Λ2+Λ3>0,Λ1+Λ4>0时满足情形5,如图2。

图2 情形5
(4)当政府单独推行社会责任、给予施工企业的惩罚与声誉惩罚的和πg+K+pE小于政府推行社会责任付出的成本Cg,施工企业单独行动获得的利益增量Δπp大于付出的成本Cp,当政府部门获得的利益增量与声誉惩罚的和αL(Δπg+Δπp)+pE大于政府部门给予施工企业的惩罚、搭便车获得的收益和推行社会责任成本的和Cg+mΔπp+J时,即Λ1<0,Λ2>0,Λ1+Λ4>0,满足情形7,如图3。

图3 情形7
2 数据模拟分析及建议
考虑到系统动力学(System Dynamics,SD)模型能够清晰地表现各系数之间的数量关系,故本文运用SD模型分析参数变化对博弈决策的影响。根据演化博弈分析建立政府部门与施工企业社会责任履行的SD仿真模型,将公共机构推动社会责任履行概率x、施工企业履行社会责任y设为状态变量,f(x),f(y)为速率变量,得到系统流图如图4。

图4 系统动力学模型
使用软件VensimPLE7.3.5进行系统动力学仿真,设定INITIALTIME=0,FINALTIME=100,TIMESTEP=0.5。根据系统动力学模型的构建原则,对模型参数初始值进行赋值:Cg=0.8,Cp=0.8,Δπg=0.5,Δπp=0.6,J=0.1,K=0.1,pE=0.1,m=0.3,n=0.2,α+β=0.9,α=0.5,L=2.1,y=0.7,x=0.5。仿真结果如图5,均衡策略是政府部门不推动,施工部门不履行MSR。

图5 仿真结果
2.1 收益增量对演化结果的影响
Δπg,Δπp是双方履行MSR各自的收益增量。保持其他参数不变,对参数Δπp分别取0.45,0.5,0.55,0.6时博弈主体的决策演化结果如图6所示,可见随着Δπp的增大,政府部门决策将由不推动向推动MSR演化,施工企业决策由不履行向履行MSR演化,最终实现双方协同履行MSR的机制。这是因为随着施工企业收益增量变大,政府部门获得“搭便车”收益变大,使自身收益由负变正,故双方都向积极行为演化。但当Δπp=0.5时,出现了政府部门积极行为的概率先上升后下降的情况,代表着政府部门推动概率虽然先增大,但随着时间的推进,由于施工企业履责意愿一直减弱,导致政府“搭便车”收益下降,政府部门推动意愿逐渐下降,最终稳定于双方均采取消极策略。对不同的Δπg进行仿真模拟,如图7,也可以得到类似的结论。因此,提高双方各自积极行为所获得的收益,有利于实现双方协同履行社会责任的机制。
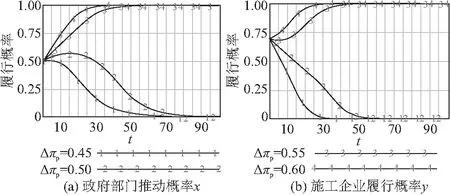
图6 Δπp对MSR履行的影响

图7 Δπg对MSR履行的影响
因此,为了增加政府部门和施工企业履行社会责任的效益增量,第一,政府部门应对履行MSR的施工企业进行额外补贴或政策优惠;第二,政府部门和施工企业都应该在不降低品质的前提下努力减少履行社会责任成本,以提高各自效益增量;第三,通过荣誉表彰来鼓励履行MSR的机构,并且做好宣传,提高该施工企业的社会形象,这对于施工企业来说也是一种效益增量。
2.2 协同收益系数L的影响
“协同收益系数”是双方合作下产生的总收益放大系数,与双方的合作程度具有正相关性。具体表现为双方由于目标相同,形成优势互补,效率加快导致总收益增大的情况。本文对协同收益系数L对MSR履行的影响也进行了仿真,如图8所示:

图8 协同收益系数L对MSR履行的影响
从图8中可以看出,双方的协同收益系数越大,双方更容易进入积极行为状态,且随着协同收益系数的增大,其收敛效应也越明显。协同收益系数一定程度上代表了合作双方的契合程度,因此在选择政府部门合作伙伴时,应当对施工企业的各项指标进行一个全面的评估,选择善于合作、与政府部门自身更契合的企业可以创造更大的收益,促进重大工程社会责任的实施。
2.3 利益分配系数的影响
由于重大工程项目利益相关者关系较为复杂,所以此处我们抽象出对整体影响较大的两方进行研究,由于存在其他利益相关者,故假设α+β=0.9。给定几组不同的α,β值,得到双方均衡策略如图9所示。显然,随着α值增大至0.5,β值减小至0.4时,双方都进入积极行为状态。然而随着α继续增大,β继续减小,政府部门策略先趋向于积极行为状态,但随着时间的推进,由于施工企业履责概率逐渐变小,政府部门“搭便车”收益减少,双方策略逐渐稳定于消极行为状态。因此,在进行重大工程项目利益分配时,选择合适的利益分配系数非常重要。

图9 利益分配系数α对MSR履行的影响
综上所述,增加双方各自履责所获收益Δπp和Δπg、协同收益系数L、设定合适的利益分配系数将使得双方更偏向于参与履责决策。但过大或过小的利益分配系数L会对重大工程项目社会责任履行起负向作用。
因此,针对如何推进社会责任履行制度落实的建议如下:
政府部门和施工企业在保持履责既定目标情况下,应通过开源节流、适当精简机构等方法减少各自的履责成本,间接增加双方履责收益,促进责任双方履行社会责任。
政府部门应该完善激励约束机制,一方面对于履行MSR的施工企业给予奖励,对不履行MSR的企业进行处罚。政府也可建立优质施工企业库,将社会责任履行作为入库的一项重要指标,对履行MSR的优质施工企业给予一些便利,如优先合作等,增加施工企业履行MSR的潜在收益。另一方面可将社会责任履行结果与施工企业的绩效挂钩,拓宽施工企业绩效评价体系,对重大工程项目全生命周期内各个阶段履责程度进行考核,保证全生命周期内社会责任的履行。
政府部门应构建高效的合作体系,设定合理的收益分配系数。政府部门不仅要选择与自身优势互补的施工企业合作以增加协同收益,还应制定合理的利益分配策略,考虑到政府作为博弈领导者,施工企业在博弈中处于劣势。因此应该对双方合作进行适当监管,如引入第三方监察、审计机构等,从而防范行为异化偏离良性轨道。
3 结论及展望
近年来我国重大工程投资建设规模空前,取得了世界瞩目的工程建设成就,但也给自然环境和工程移民带来了沉重的负担,亟需通过有效的社会责任管理才能形成多方协同履行社会责任的格局,保障重大工程建设的顺利实施、安全运行和可持续发展。
本研究从重大工程参与主体的履责决策及其影响因素的角度入手,通过演化博弈、系统动力学模型模拟了政府部门和施工企业双方履责的决策过程,分析了重大工程项目中双方履责决策的影响因素及各影响因素对它们的影响程度,并且为如何推动重大工程项目社会责任的履行提供了有效建议。但研究也存在一定的局限性,本文缺少一些实际的数据以支撑模型的构建和数值实验,这将是未来研究中一个很重要的方向。另外,本文为了分析简便,只选取重大工程项目中影响较大的政府部门、施工企业进行博弈分析,后续将考虑多利益相关者博弈的问题。

