钨合金球形破片侵彻低碳钢的弹道极限速度计算模型
刘铁磊, 徐豫新,2, 王晓锋, 张鹏, 张健
(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.北京理工大学 重庆创新中心, 重庆 401120;3.中北大学 机电工程学院, 山西 太原 030051)
0 引言
破片是杀爆战斗部主要毁伤元素,可用于对人员、车辆、轻型装甲等目标进行毁伤,通常以破片的弹道极限速度表征破片的毁伤能力。
国内外早已开展各类破片对低碳钢的侵彻研究。Golsdmith等通过弹道枪试验获取了6~9 mm直径钢球穿透1.57 mm厚1020钢的速度降;谭多望等通过试验掌握了6~8 mm直径钨合金球形破片对6~12 mm厚Q235钢板的侵彻能力;陈志斌通过试验获得4.75 mm直径钨合金球形破片对6~10 mm厚Q235钢板弹道极限速度;午新民、徐豫新对钨合金球形破片侵彻10~20 mm厚Q235钢板的侵彻机理开展研究,得到相应破片与靶板(简称弹靶)条件下的弹道极限速度。近5年来,仍有许多研究者对钨合金破片侵彻Q235钢板的弹道极限速度进行进一步的研究,如:朱曦光等、李金福等、张钰龙等开展了钨合金球形破片垂直侵彻Q235钢板试验,获得了9 mm直径钨合金球形破片对8~9 mm厚Q235钢板的弹道极限速度。然而,已有研究均为具体弹靶条件下的弹道极限速度获取试验,得到的计算模型普适性有限,难以支撑0~2 000 m/s速度范围内钨合金球破片侵彻多种低碳钢板的弹道极限速度计算。
本文针对钨合金球形破片对低碳钢的刚性、塑性、侵蚀和破碎侵彻,系统分析钨合金球形破片侵彻低碳钢的破坏特征,建立计算精度高、适用性广的弹道极限速度计算模型。
1 模型的建立
1.1 破片侵彻特征
破片在不同速度下侵彻靶板,会产生不同的侵彻特征。因此,首先从破片侵彻特征着眼,对破片侵彻特征改变的速度阈值进行讨论,为后续弹道极限速度计算模型的建立提供支撑。
1.1.1 刚性侵彻
文献[10]表明,当破片以小于500 m/s速度撞击靶板时破片仍保持球形,未发生明显变形(见图1),整个侵彻过程中破片可近似视为刚体。
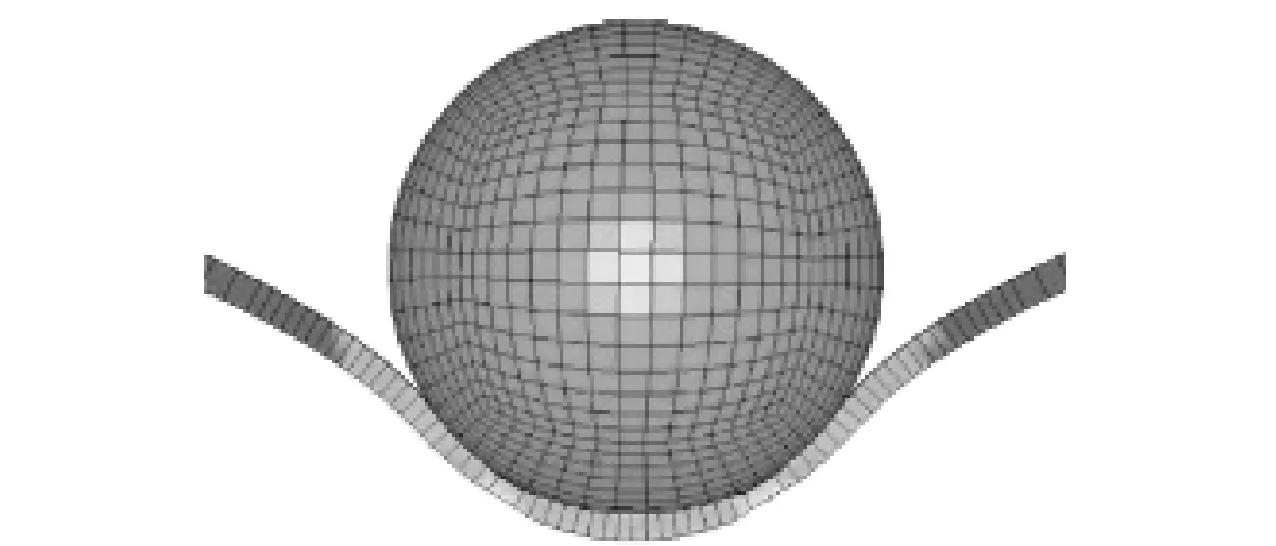
图1 破片刚性侵彻[10]Fig.1 Rigid penetration of fragments[10]
1.1.2 塑性侵彻
根据文献[11]可见,当破片以500~1 000 m/s速度撞击靶板时,破片因受到靶体阻力发生屈服,产生塑性变形(见图2)。

图2 破片塑性变形[11]Fig.2 Plastic deformation of fragments[11]
对于塑性侵彻,Rosenberg等研究了头部形状为半球形长杆侵彻金属靶板时由刚性侵彻转变到非刚性非侵蚀侵彻时的着靶速度阈值,认为在杆体侵彻过程中,若杆体发生塑性变形,则杆体端面应力为+,其中为杆体材料动态压缩屈服强度,为杆体端面压强。相应地,弹靶界面靶板方向同样存在压强与杆体端面应力平衡,其大小为+05,05为靶板驻点压强,为靶板密度,为杆体速度,为靶板对杆体的侵彻阻抗,从开始侵彻到侵彻完成期间的平均侵彻阻抗为

(1)
为靶板材料动阻抗,为靶板材料屈服强度。
根据牛顿第三定律,力平衡方程为
+=05(+3)+05
(2)
对于93W钨合金,动态屈服强度为186 GPa,则钨合金材料发生塑性变形阈值速度为
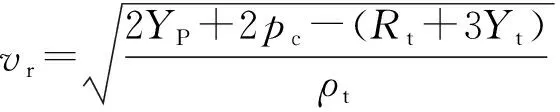
(3)
式中:=3。Rosenberg等根据静态空腔膨胀原理,推导计算式为
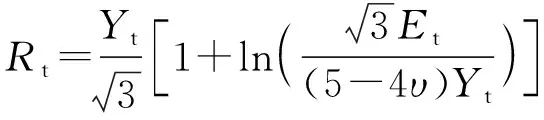
(4)
式中:为靶板材料弹性模量;为靶板材料泊松比。
113 侵蚀侵彻
根据文献[6]可见,当破片以高于1 000 m/s的速度撞击靶板时,破片质量开始减少,表明破片在侵彻过程中发生了侵蚀(见图3)。

图3 破片侵蚀[6]Fig.3 Erosion of fragments[6]
对于侵蚀侵彻,Tate对长杆弹高速侵彻时固体与流体转变阈值速度进行研究,发现当弹靶界面运动速度超过弹体材料塑性波速时,弹体材料发生侵蚀现象,侵蚀速度为
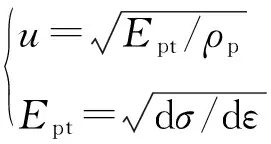
(5)
式中:为破片材料切线模量;为破片材料密度;dd为屈服点后应力- 应变(-)曲线斜率。
因此,当破片侵蚀时可近似将破片视为流体,根据伯努利流体计算公式,有
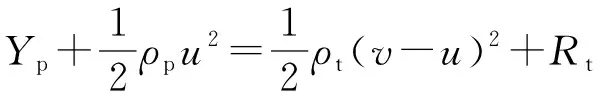
(6)
联立(4)式、(5)式、(6)式,可得到钨合金破片侵蚀变形阈值速度为
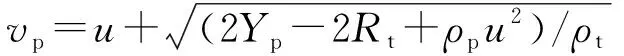
(7)
由文献[16]中钨合金拉伸应力- 应变曲线,可得到钨合金切线模量=32 GPa,计算得到破片材料侵蚀阈值速度。
114 破碎侵彻
由文献[17-18]可知,当破片以高于1 400 m/s速度冲击靶板时破片完全破碎,一部分以熔渣碎片的形式残留在靶板穿孔内部,贯穿靶板破片也呈现破碎化特征(见图4)。

图4 破片破碎[17]Fig.4 Fracture of fragments[17]
当破片着靶速度较高时,破片在侵彻过程中出现完全破碎,Sun等给出了忽略靶板强度的着靶速度阈值计算方法:
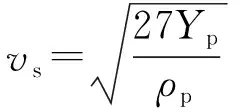
(8)
1.2 破片弹道极限速度模型
对有关侵彻分析模型,Anderson等已经做了较为详述的介绍。由于分析模型推导过程较为困难,在数据量充足的情况下,经验模型不失为较好的方法。
121 现有模型的局限
午新民等根据弹道试验结果,建立破片弹道极限速度计算模型形式如下:
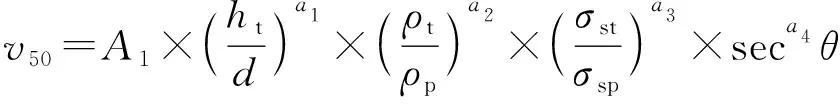
(9)
式中:为弹道极限速度;为拟合系数;为靶板厚度;为破片直径;为靶板材料拉伸极限强度;为破片材料拉伸极限强度;为着靶倾角;、、、为拟合指数。
(9)式是基于破片侵彻装甲钢试验得到弹道极限速度计算模型,其适用于弹靶厚度比08~20,着速在500~2 000 m/s。对于装甲钢,通过已有试验可见,靶板主要失效模式为剪切破坏下的塞块形成。通过已有试验结果可见低碳钢的破坏模式并不同于装甲钢,在侵彻过程中塑性变形特征比装甲钢明显,先压缩再形成塞块。因此模型需要增加可反映塑性变形的参数。
此外,根据11节分析可知,不同着靶速度下破片会产生不同破坏模式。因此,需要根据速度区间分别进行计算。
122 新模型的建立
为在更广泛速度区间内构建弹道极限速度计算模型,基于(9)式对破片侵彻过程中主要破坏特征下的计算模型进行分析。
对于刚性侵彻,除(9)式所示的弹靶厚度、弹靶强度、弹靶密度外,弹靶材料延伸率同样是影响侵彻的主要因素,然而对于刚性破片,材料延伸率无需考虑,同时(9)式中破片的拉伸极限强度可改成屈服强度。据此建立计算模型为
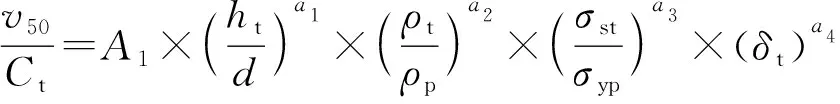
(10)
式中:为靶板材料塑性波波速;为靶板材料延伸率。(10)式的适用速度范围为0<≤。
对于塑性侵彻,破片发生了变形,此时需考虑破片材料的延伸率。由此,在(10)式上反映破片材料延伸率,建立计算模型为
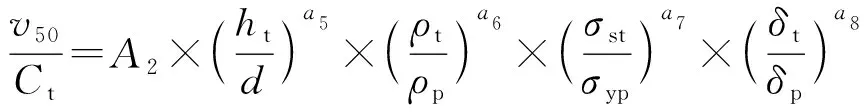
(11)
式中:为拟合系数;、、、为拟合指数。(11)式的适用速度范围为<≤。
对于侵蚀侵彻,破片在与靶板接触地方发生侵蚀,对侵彻起主要作用的是破片和靶板材料的拉伸极限强度,整个侵彻过程同样包含塑性变形。因此,破片和靶板材料的延伸率均需予以考虑;据此可建立计算模型为
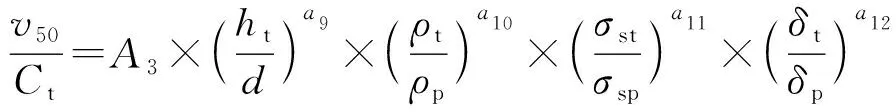
(12)
式中:为拟合系数;、、、为拟合指数。(12)式的适用速度范围为<≤。
对于破碎侵彻,破片呈现流体的性质,此时靶板材料拉伸极限强度、延伸率决定了破片的侵彻深度,破片材料的强度不再考虑;据此建立计算模型为
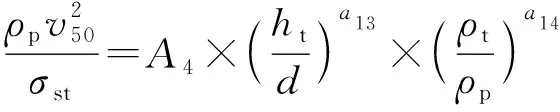
(13)
式中:为拟合系数;、为拟合指数。(13)式的适用速度范围为>。
综上所述,钨合金球形破片侵彻低碳钢的弹道极限速度计算模型为
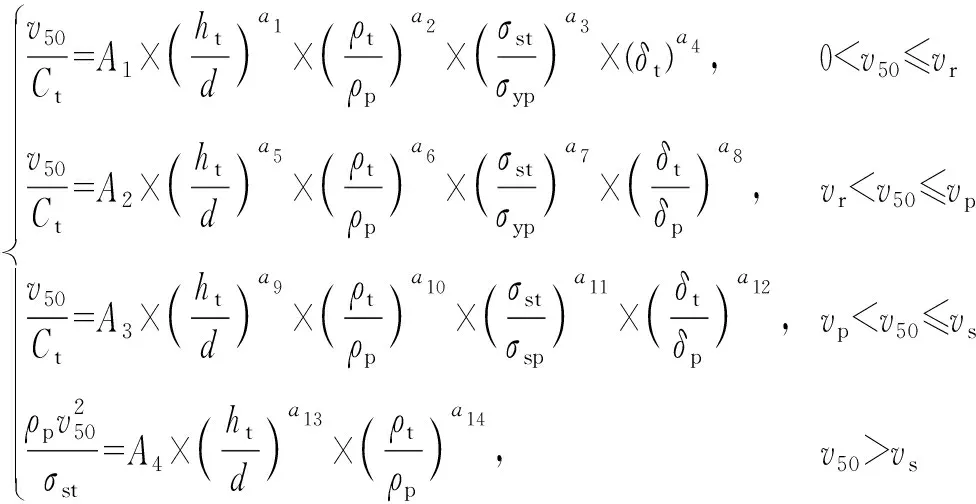
(14)
(14)式系统考虑了破片材料在不同着靶速度下的侵彻破坏特征,含18个待定系数,这18个系数可基于试验数据获得。
2 破片侵彻试验
2.1 试验设计
为了获得破片侵彻低碳钢板的弹道极限速度来验证模型计算的可靠性,设计了破片对低碳钢板的侵彻试验,如图5所示。
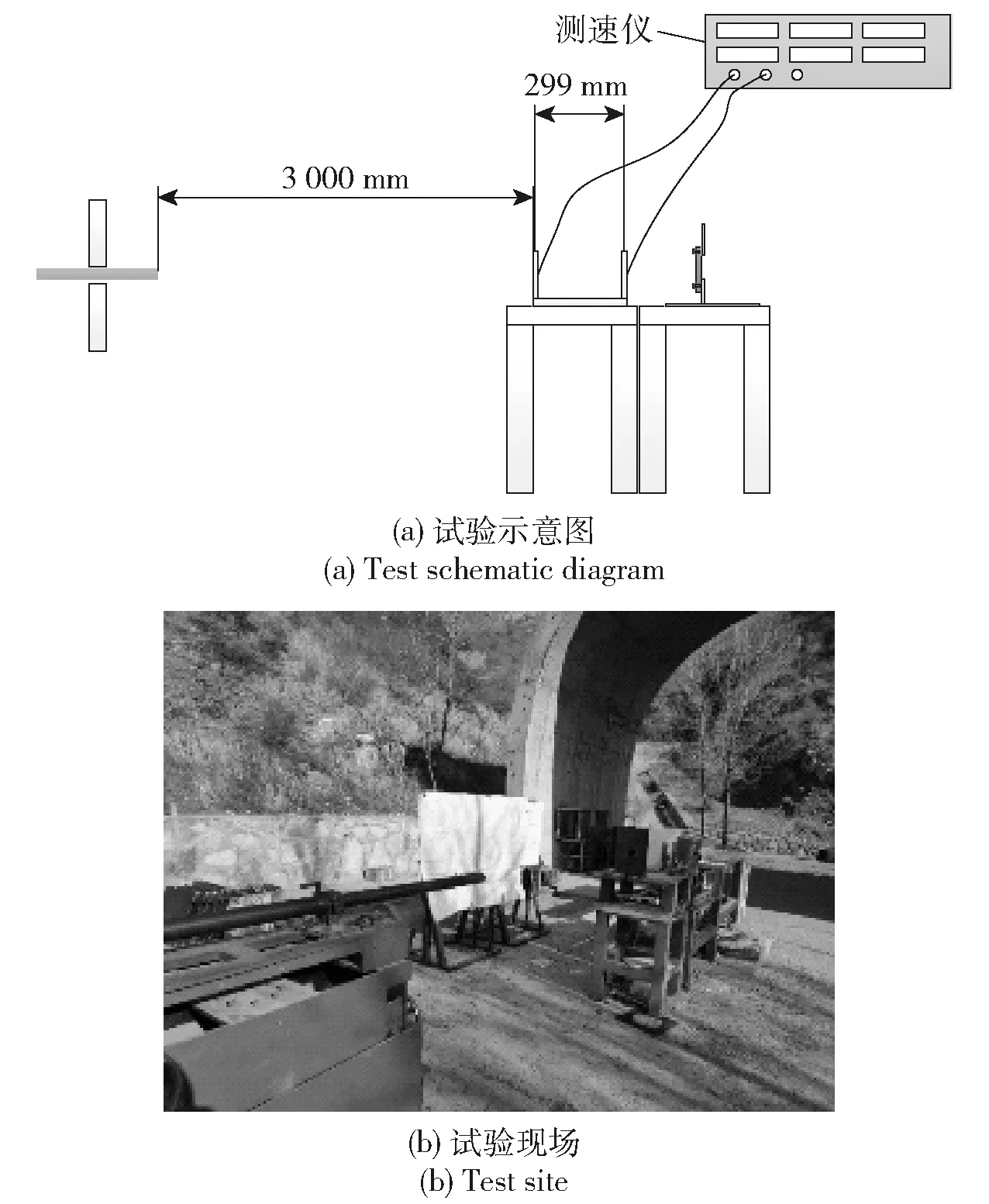
图5 弹道试验设计Fig.5 Ballistic test design
采用12.7 mm弹道枪进行加速,破片安装在弹托内,出枪管后受空气阻力作用,弹托与破片分离,如图6所示。由图6可知:试验中破片与弹托可靠分离。破片着靶速度通过靶前测速靶获得。

图6 破片弹托分离(速度287 m/s)Fig.6 Separation of fragment and sabot with velocity of 287 m/s
2.2 试验结果
对Q235、Q345E两种低碳钢板进行破片侵彻试验,试验之前,对靶板的静力学性能进行测试,破片静力学性能参数由供应商提供,弹靶主要力学性能如表1所示。
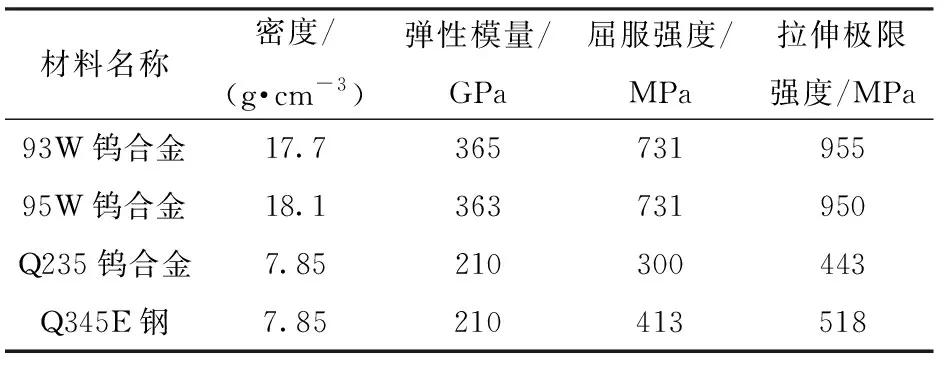
表1 弹靶力学性能
通过破片侵彻试验得到直径为6 mm、7 mm和 8 mm 钨球垂直侵彻4 mm、6 mm、8 mm厚Q345E钢板,3 mm、6 mm厚Q235钢板的弹道极限速度,结果及试验后部分靶板如表2、图7和图8所示。
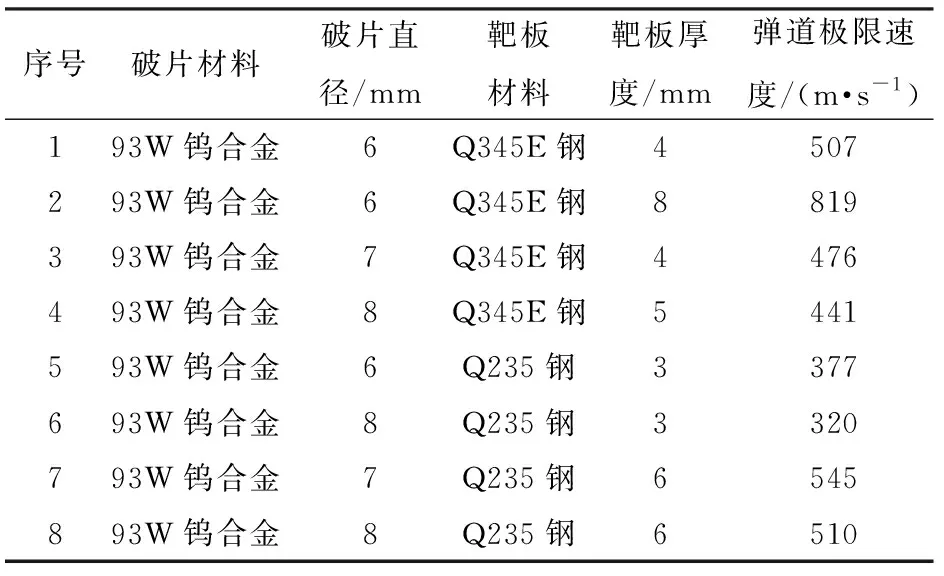
表2 弹道试验结果

图7 破片对4 mm厚Q345E钢靶板侵彻情况Fig.7 Fragments penetrate Q345E plate with 4 mm thick

图8 破片对8 mm厚Q345E钢靶板侵彻情况Fig.8 Fragments penetrate Q345E plate with 8 mm thick
3 模型求解
3.1 拟合数据
根据文献[4-9]及2.2节试验数据进行模型系数获取,试验数据列于表3中。
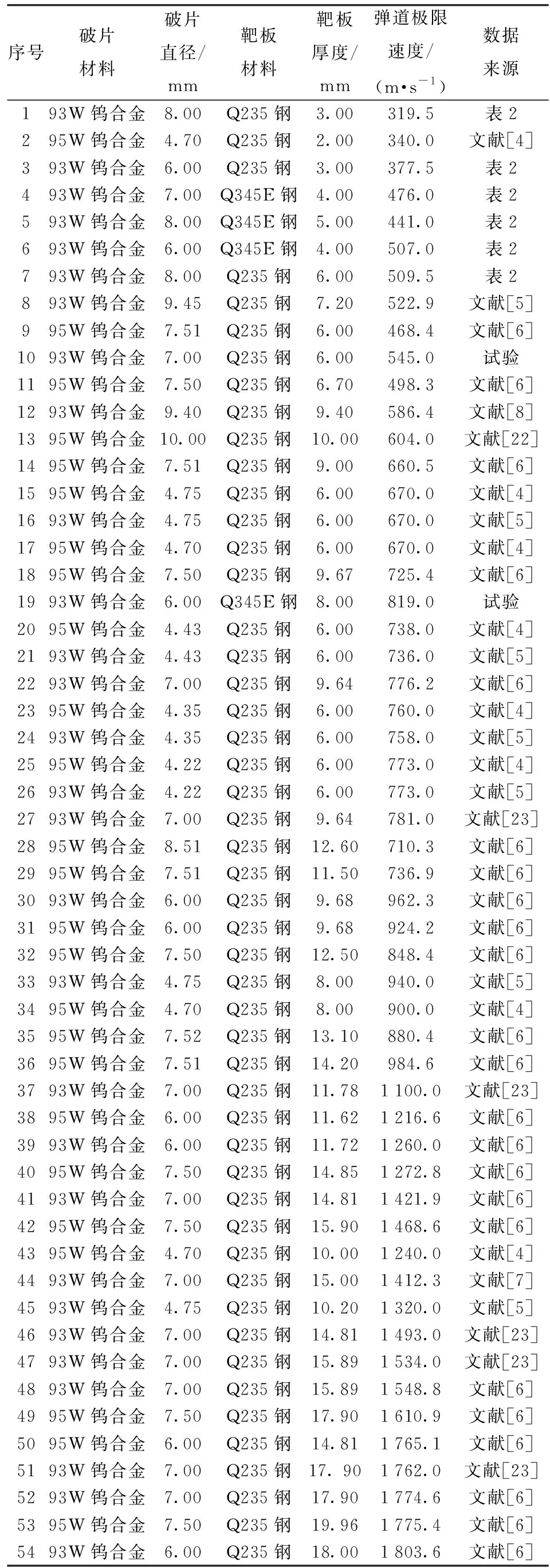
表3 弹道极限速度试验数据
图9显示了表3数据中相对弹靶厚度比和弹道极限速度的非线性关系。由图9可见:低碳钢板弹道极限速度随着弹靶厚度的增加而逐渐减少。
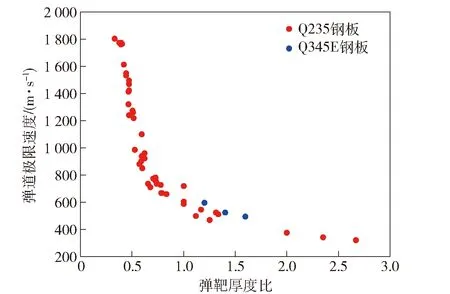
图9 弹道极限速度关于弹靶厚度比分布Fig.9 Distribution of ballistic limit velocity with thickness ratio of projectile to target
3.2 速度阈值
根据表2中力学性能参数和(3)式、(7)式、(8)式,计算弹道极限速度模型中的分段速度阈值如表4所示。由表4可见,靶体材料对破片破坏特征改变的着靶速度阈值影响不大。
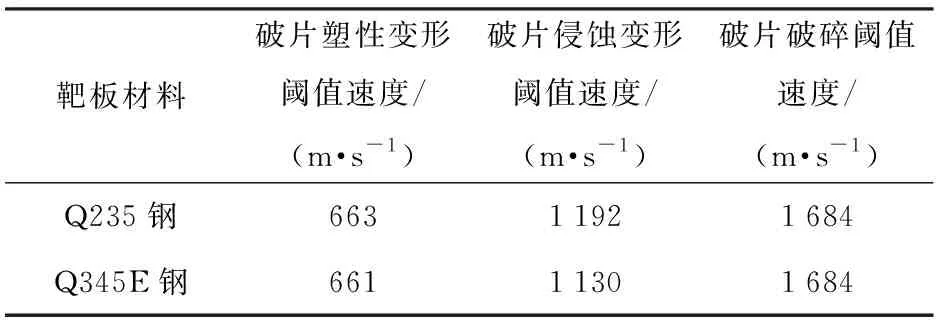
表4 破片变形阈值
破片变形阈值速度如表4所示,对比1.1节的破片侵彻特征,可见所求变形阈值速度在一定程度上与试验结果符合。例如,文献[11]的试验结果,显示在500~1 000 m/s的着靶速度下,破片呈现非侵蚀塑性变形的特征,与所求662 m/s的塑性变形阈值速度是相容的。
3.3 系数获取
试验获得弹道极限速度如图10所示,不同靶板对应的弹道极限速度和速度阈值以不同的颜色进行区分。由图10可见,靶板类型对破片的侵蚀速度阈值有一定影响。由于现有样本量分布不均,在此取破片侵彻两类靶板的平均侵蚀阈值速度作为破片侵蚀变形阈值速度进行计算。
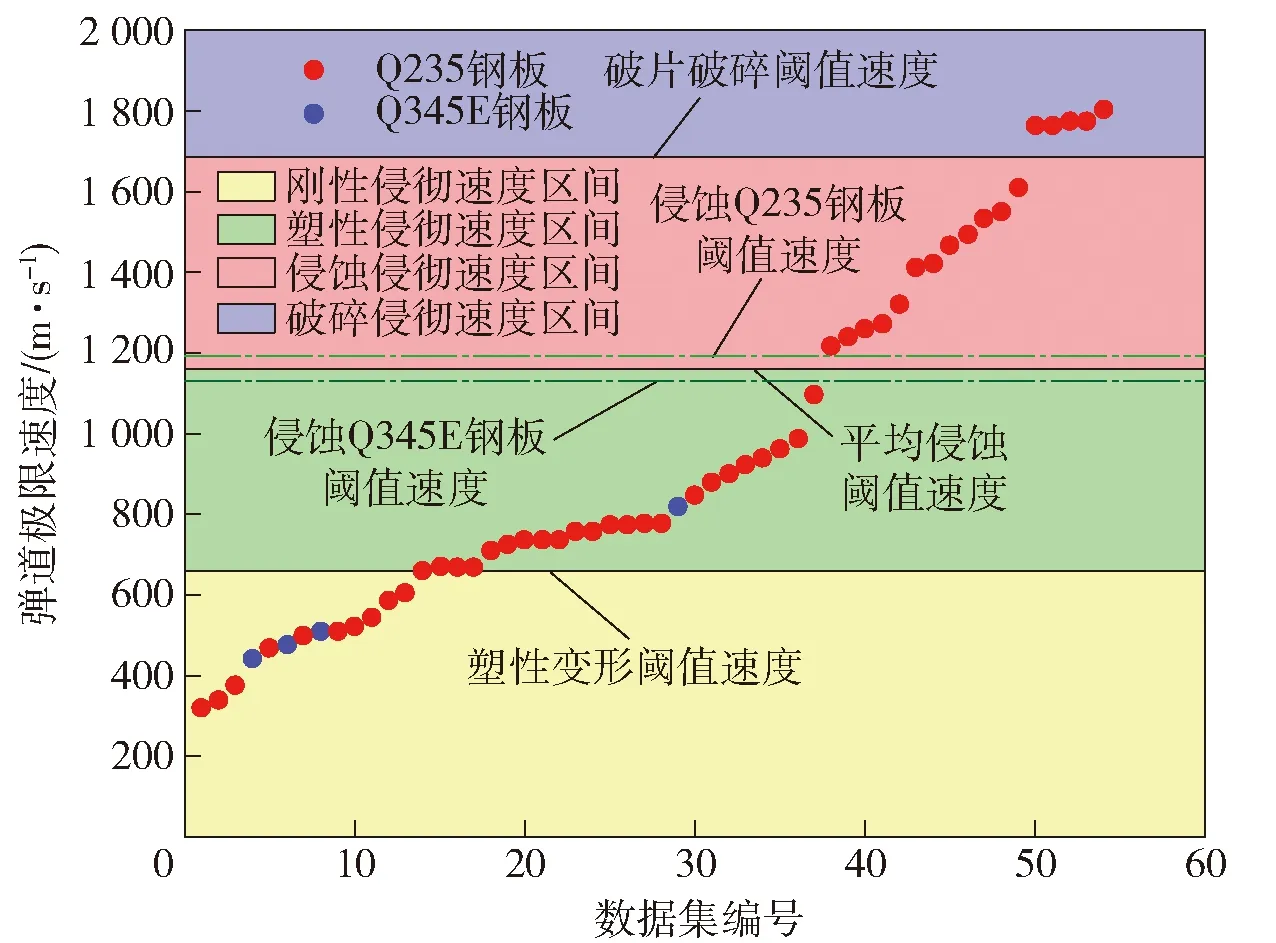
图10 试验数据分布Fig.10 Distribution of test data
图9和图10分别体现了弹道极限速度与弹靶厚度比的关系,弹道极限速度与破片变形阈值速度之间的联系。将弹靶厚度比与破片变形阈值速度关联,可得弹道极限速度与弹靶厚度比之间的联系,如图11所示。
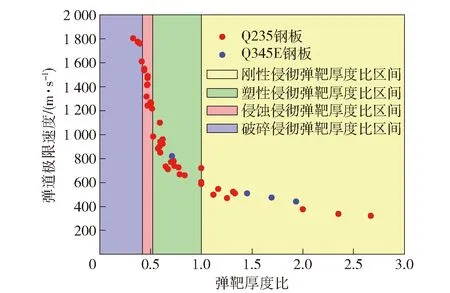
图11 弹道极限速度随弹靶厚度比的变化Fig.11 Variation of ballistic limit velocity with thickness ratio of projectile to target
图11反映了破片极限穿透靶板时,不同弹靶厚度比与破片侵彻类型之间的联系。弹靶厚度比1<≤27时,破片以刚性侵彻为主;弹靶厚度比052<≤1时,破片以塑性侵彻为主;弹靶厚度比042<≤052时,破片以侵蚀侵彻为主;弹靶厚度比033<≤042时,破片以破碎侵蚀为主。由此(14)式隐式形式的弹道极限速度计算模型变为显示形式:

(15)
331 信赖域方法
模型(15)式为非线性方程组,对于此方程组,可采用迭代算法求解。信赖域反射方法是一种求解非线性优化问题的方法,其原理是利用目标式的泰勒2阶展开代替目标式搜索最优步长,较一般线搜索方法收敛更快,求解方法如下:
()是目标函数,在的邻域定义为{∈|‖-‖≤},为信赖域半径,则在邻域处泰勒展开,定义信赖域子问题如下:
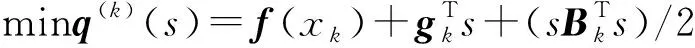
(16)
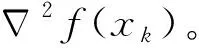
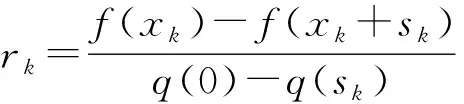
(17)
若>075,则表明接近程度好;此时可扩大信赖域,令+1=2;若<075,则可维持信赖域半径,令+1=;若<025,则表明离真实值较远,进一步缩小信赖域半径,有+1=025‖‖。随后在新信赖域半径内,对信赖域子问题求解,直到试探步长收敛接近于0。
若采用信赖域反射方法,则需要对解的取值范围进行约束。根据已有研究,靶板厚度、靶板强度、靶板密度、靶板材料延伸率与弹道极限速度呈现正相关;破片密度、破片强度、破片直径与弹道极限速度呈现负相关。因此,(14)式回归系数取值应大于0;为了对模型的回归系数在相同尺度下进行对比,分析不同物理参量在相同条件下的重要程度,在此可令模型系数、、均为1。
采用上述方法,(14)式系数回归后模型为
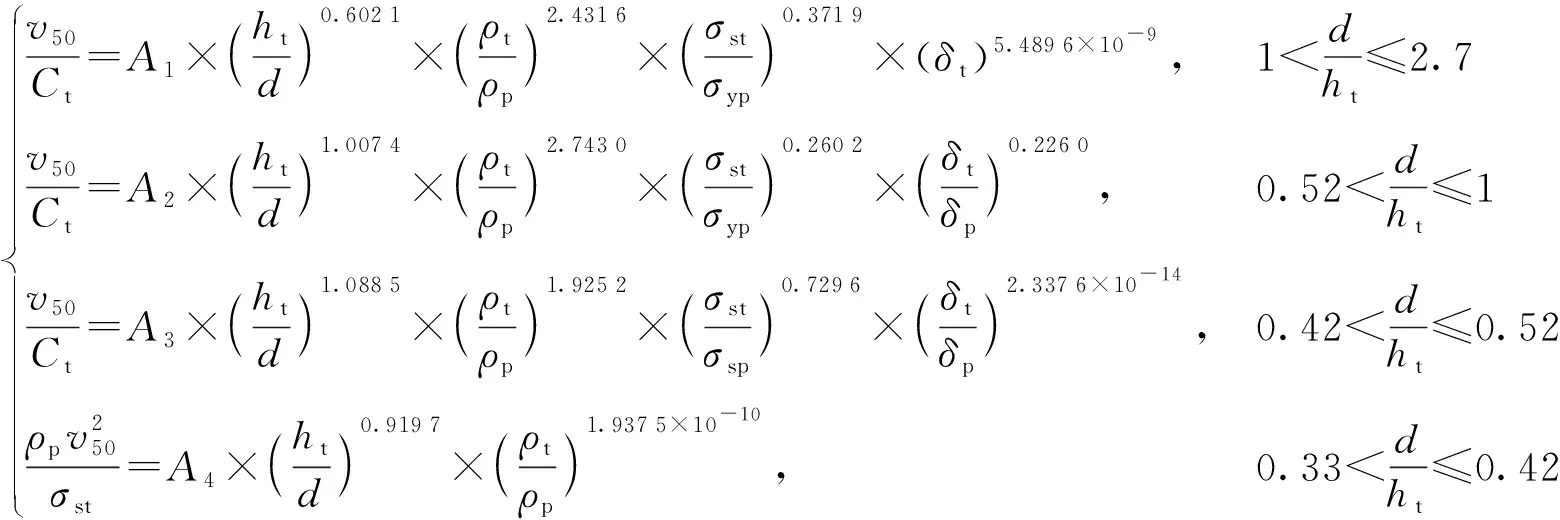
(18)
对(18)式拟合系数四舍五入后保留两位小数,方程中出现趋于0项即指数为0,则表明该项在方程中不起作用。因此去掉指数为0项可进一步化简为
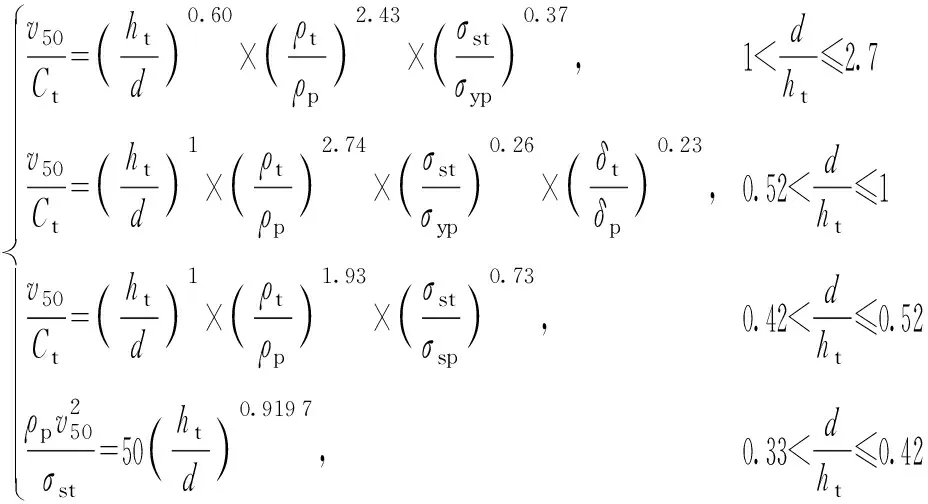
(19)
(19)式的形式和前面理论分析有一些出入,如刚性和侵蚀侵彻计算方程不含延伸率项,破碎侵彻方程的弹靶密度项为0,反映了速度区间阈值和信赖域拟合方法在方程求解上的特点。在信赖域方法中,信赖域半径等于邻域1的范数,因此可视为求信赖域子问题时加入了L1正则项。而L1正则化使解的特征稀疏化,具备特征选择功能。
通常,材料延伸率和屈服强度是影响弹靶侵彻的因素,其中材料延伸率反映材料塑性应变的性能,屈服强度反映材料抵抗塑性应变能力。对于破片侵彻低碳钢问题,由于靶板存在明显塑性流动现象,在方程中考虑这两类因素,但对于因素的影响因子相对大小是未知的。计算结果证明,在不同着靶速度范围内,两个物理量的影响存在差异。
332 结果验证
图12所示为弹道极限速度试验结果与模型计算结果对比图。由图12可见,弹道极限速度模型计算结果与试验结果基本一样,表明系数的可靠性。图13所示为模型计算结果与试验结果的相对误差,采用(20)式计算方法得到相对误差,得到最大误差为82,表明计算模型具有较高的精度。
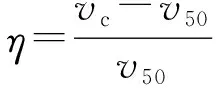
(20)
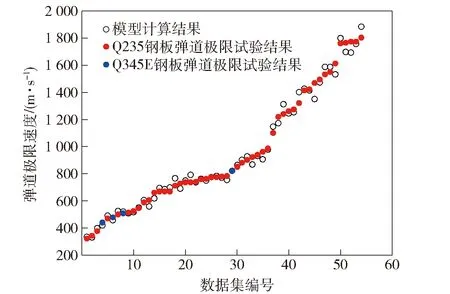
图12 试验结果与计算结果对比Fig.12 Comparison of test results and calculated results
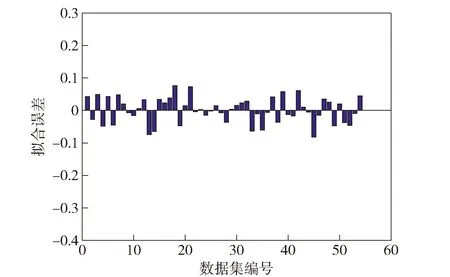
图13 试验结果与计算结果误差Fig.13 Error between test results and calculated results
由(19)式可见:弹靶相对密度的系数绝对值最大,可判定其是影响弹道极限速度的主要因素;弹靶厚度比和弹靶相对强度是影响破片弹道极限速度的次要因素。
4 误差分析与验证
4.1 误差分析
采用相同的方法与试验数据,在相同求解区内,对文献[4-5,22]中模型进行系数获取,并比较新旧模型计算结果与试验结果之间的平均绝对误差(MAD)、平均相对误差(MRE)和最大偏差(ME),计算式如下:
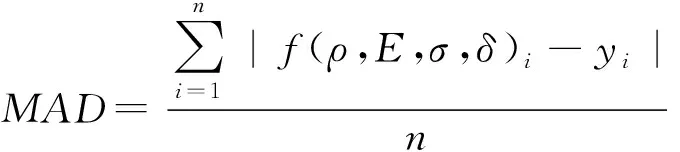
(21)
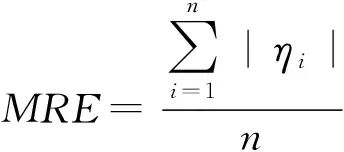
(22)
=max{||,||,…,||}
(23)
式中:(,,,)为计算获得数值;为试验获得数值;为数据量;为计算值与试验值偏差。
文献模型计算结果如图14~图16所示,新旧模型计算结果与试验结果之间误差如表5所示。
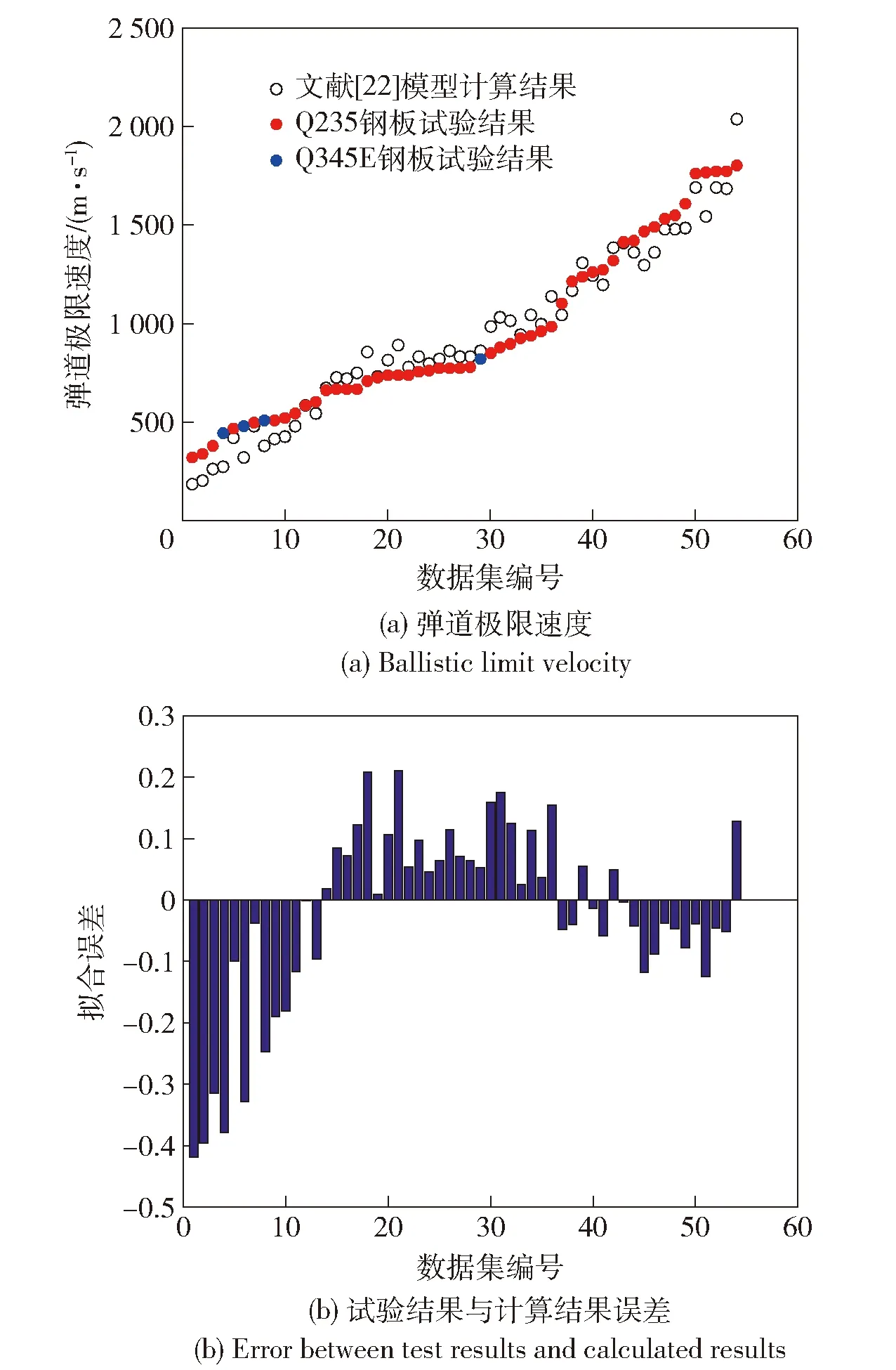
图14 文献[22]模型计算结果与试验结果对比Fig.14 Comparsion between the calculated results in Ref.[22] and the test results
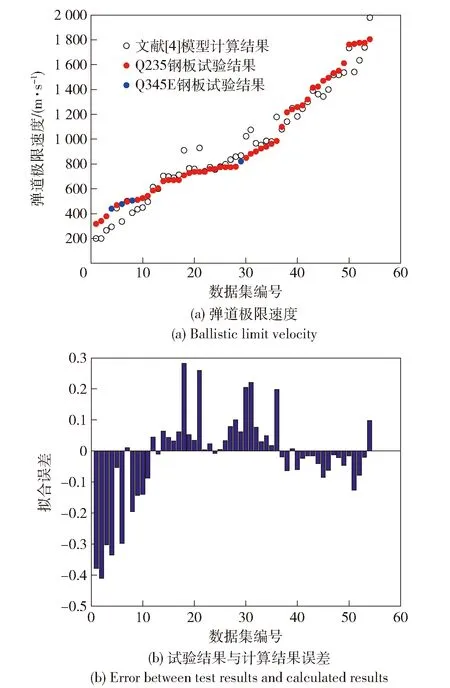
图15 文献[4]模型计算结果与试验结果对比Fig.15 Comparsion between the calculated results in Ref.[4] and the test results
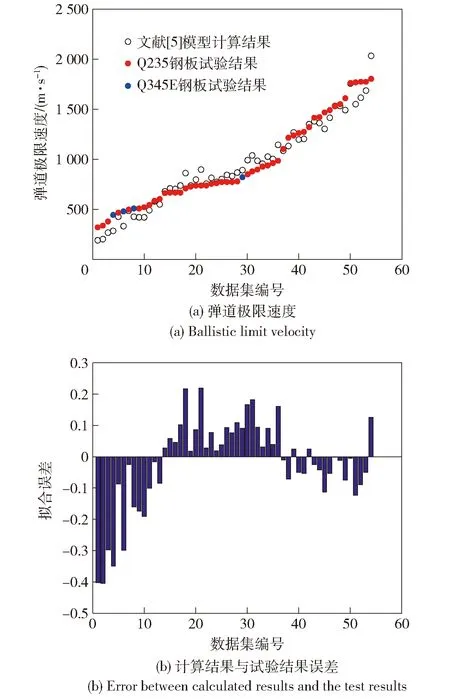
图16 文献[5]模型计算结果与试验结果对比Fig.16 Comparison of the calculated results in Ref.[5] and the test results
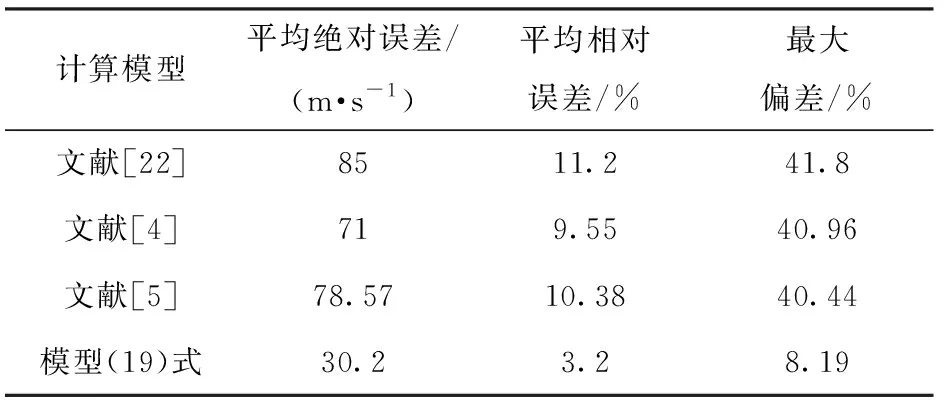
表5 模型计算结果与试验结果误差
由图14(a)、图15(a)、图16(a)可见:模型计算值和试验值趋势相同。各公式适用范围集中在 611~1 800 m/s区间,比本文模型的适用范围要窄。对比各模型计算结果和试验结果的误差直方图,现有模型的误差均呈现中间数据为正偏差、两头数据为负偏差的特点,且偏差绝对值均较大,一定程度上反映了现有模型的局限性。图17所示为误差直方图对比。
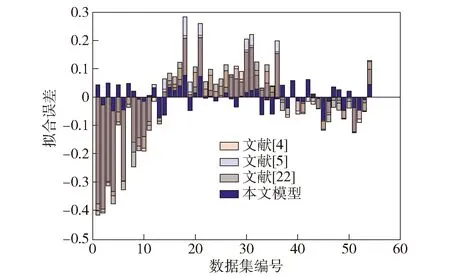
图17 误差直方图对比Fig.17 Error histogram
由表5可见:本文模型较文献模型计算精度具有提升。其中,本文模型的平均相对误差为3.2%,平均绝对误差为30.2 m/s,最大偏差为8.2%,均低于文献模型计算结果。可见本文模型在300~1 800 m/s的速度范围内较文献模型在计算精度方面具有优越性。
4.2 模型验证
破片侵彻低碳钢板的弹道极限速度数据全部参与模型系数拟合计算,因此不能用弹道极限速度数据对公式进行验证。然而,可以对比模型(19)式预测弹道极限速度和单枚破片在一定初速下侵彻靶板的穿透结果,当靶板未穿透时,预测弹道极限速度应大于破片初速,以此对模型的正确性进行有限验证(见图18)。
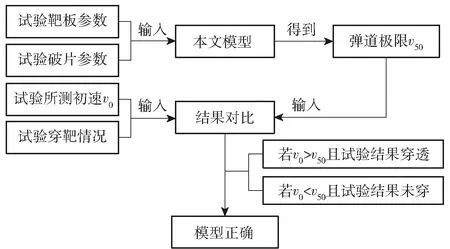
图18 验证方法Fig.18 Validation method
验证数据来源于李金福等、徐豫新等、赵晓旭等的试验。弹靶材料、厚度、试验结果和模型计算结果如表6所示。
表6为对模型(19)式的验证结果,破片侵彻速度范围从500~1 900 m/s。结果显示模型(19)式:在侵彻速度范围为500~1 800 m/s时,可以对弹道极限速度进行较好的预测;当侵彻速度超过1 800 m/s,或弹靶厚度比小于0.33时,弹道极限速度预测结果不佳。
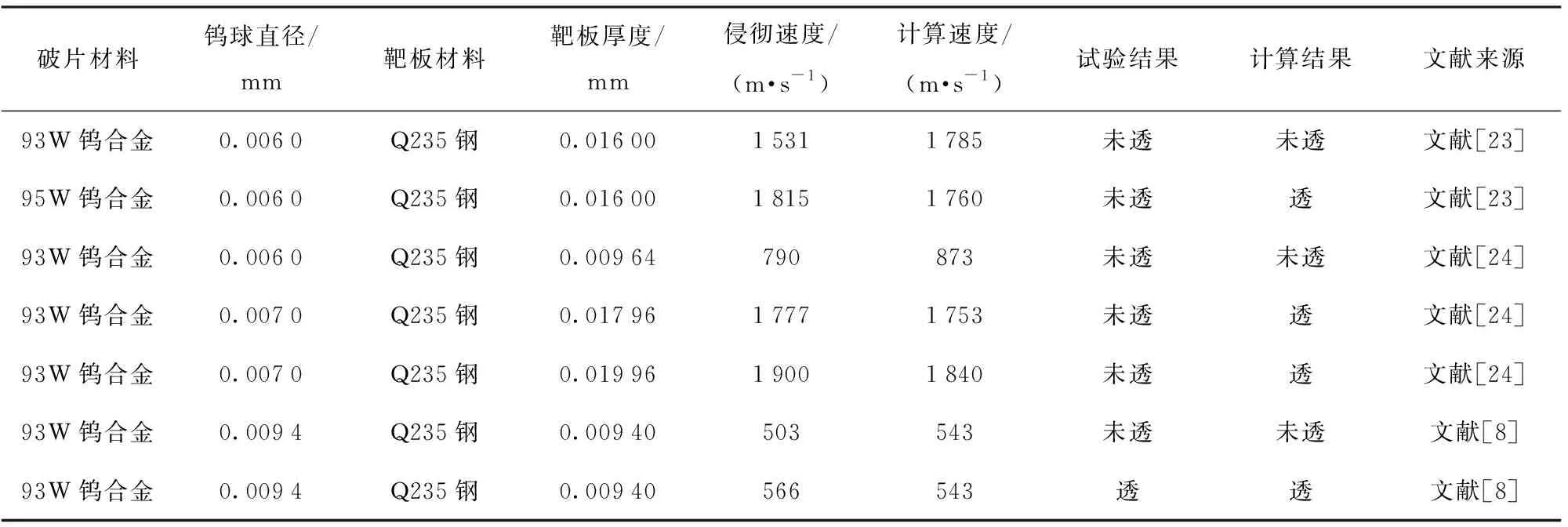
表6 模型验证
5 结论
本文针对钨合金破片对低碳钢侵彻建立了具有更加普适性的弹道极限速度计算模型,对不同速度区间内破片侵彻中的破坏特征进行讨论,提出不同破坏特征变化的着靶速度阈值求解方法;建立基于弹靶力学性能参数的弹道极限速度计算模型,并基于信赖域方法获得了模型系数。根据已有试验数据分析了所建立模型计算的精度。得出主要结论如下:
1)通过对比分析,所建模型在300~1 800 m/s着靶速度区间内或0.33~2.70的弹靶厚度比内,计算精度较高,具有实用价值。
2)基于不同速度下的侵彻规律建立分段模型,较一般模型可取得更好的计算精度。
3)对于含约束条件的寻优问题,信赖域方法可在全局取得收敛性,解更具有普遍性。

