基于证据理论层次分析法的云贝叶斯网络在预警雷达毁伤效果评估中的应用
邓力源, 杨萍, 刘卫东, 汪江鹏
(火箭军工程大学 基础部 数学室, 陕西 西安 710025)
0 引言
目标毁伤效果评估作为作战能力分析与火力规划研究的基础,一直是作战问题研究的热点之一。目标毁伤效果评估方法主要有贝叶斯网络法、毁伤树法、故障树法、作战环法、神经网络法、模糊综合评判法等,这些方法在目标毁伤效果评估中得到了较为广泛的运用,但在处理具有一定关联性的定性、定量指标等不确定性与模糊性较强的问题时,评估效果准确性欠佳。
云模型是一种能够实现定性概念与定量概念之间相互转化的数学模型,在处理不确定性与模糊性问题上有独特的优势,已运用于质量管理、应急决策、风险评估等领域。云模型在军事领域的应用也十分广泛,李琳琳等构建了作战指挥控制系统的效能评估指标体系,引入综合云模型对体系效能进行了评估。范阳涛等针对军队信息化条件下军事训练的新特点,提出了基于云模型的军队信息化条件下军事训练评估方法。刘崇屹等提出一种基于改进层次分析(AHP)法与云模型的质量评估方法,弥补了传统导弹雷达导引头质量评估方法的不足。董华清等提出一种结合云理论与模糊模型的综合评估方法,对远程预警系统的性能进行了合理评估。王双川等针对灰色云模型在解决实际问题中的局限性,建立了非对称灰色云模型,并对装备维修保障系统的效能进行了评估。
云模型也广泛运用于目标毁伤效果评估中。张成等根据云重心评判法原理,提出一种基于云重心评判法的目标毁伤效果评估方法,并应用于对空军基地毁伤效果的评估。杜诗瑞等在装甲目标的毁伤评估中引入云模型,将装甲目标的物理毁伤度值转化为功能毁伤度值与总体毁伤度值。
同时,将云模型理论与贝叶斯网络推理思想相结合,在求得目标各毁伤等级概率的同时,亦可求得具体毁伤值。曲婉嘉等结合云模型强大的知识表达能力与贝叶斯网络在推理方面的优势,构建了基于雷达目标的贝叶斯网络毁伤模型,使用蒙特卡洛法进行参数学习得到条件概率表,通过推理求得目标各毁伤等级的概率,并利用云模型将概率值转化为具体毁伤值。李阳等构建了基于图像目标的贝叶斯网络毁伤模型,结合试验数据,使用最大似然估计法进行参数学习得到条件概率表,通过推理求得目标各毁伤等级概率,并利用云模型将概率值转化为具体毁伤值。
文献[19]在构建条件概率表时使用的蒙特卡洛法虽然能够在一定程度上弥补数据样本缺失的不利影响,但依靠随机试验得到的结果依然可能偏离实际。文献[20]在构建条件概率表时使用的最大似然估计法对实验数据的要求较高,若实验数据出现缺漏或记录错误,则所得结果可信度必然受到影响。
除了文献[19]中使用的蒙特卡洛法与文献[20]中使用的最大似然估计法,实际问题中,在给定贝叶斯网络拓扑结构的前提下,还可依据专家经验,通过引用直觉模糊函数、相对比较推断等方法得到条件概率。但传统的依据专家经验推导条件概率的方法因各专家在研究领域、知识结构、认知水平、思维模式等层面的区别,所得结果往往是不完整或者片面的。
对预警雷达的毁伤方式主要有硬毁伤模式与软毁伤模式两种类型。其中,硬毁伤模式即利用各型空、地武器平台发射导弹对预警雷达目标实施精确打击;软毁伤模式即可利用先进的电子干扰平台对预警雷达实施针对性干扰,以使得预警雷达部分或完全丧失作战能力。本文主要以针对预警雷达的软毁伤模式为研究对象,在传统贝叶斯网络模型的基础上引入云模型,建立预警雷达遭受电子干扰平台干扰的软毁伤效果评估模型。
针对传统依靠专家经验推导条件概率方法的局限性,本文采用结合证据理论(DS)与AHP法的DS/AHP方法确定各节点条件概率值,解决传统方法在确定条件概率过程中存在的问题。同时结合云模型理论与贝叶斯网络推理思想,在求得预警雷达各毁伤等级概率的同时,亦可求得各毁伤等级对应的具体毁伤值。最后,通过数学分析软件MATLAB中的联合树法实现预警雷达毁伤效果的评估。
1 基于DS/AHP云贝叶斯网络的目标毁伤效果评估流程
贝叶斯网络和云理论在推理能力与知识表达能力方面各有所长。云贝叶斯网络是一种结合了贝叶斯网络的推理能力与云模型的知识表达能力,兼具随机性与模糊性的推理模型,其推理流程如图1所示。
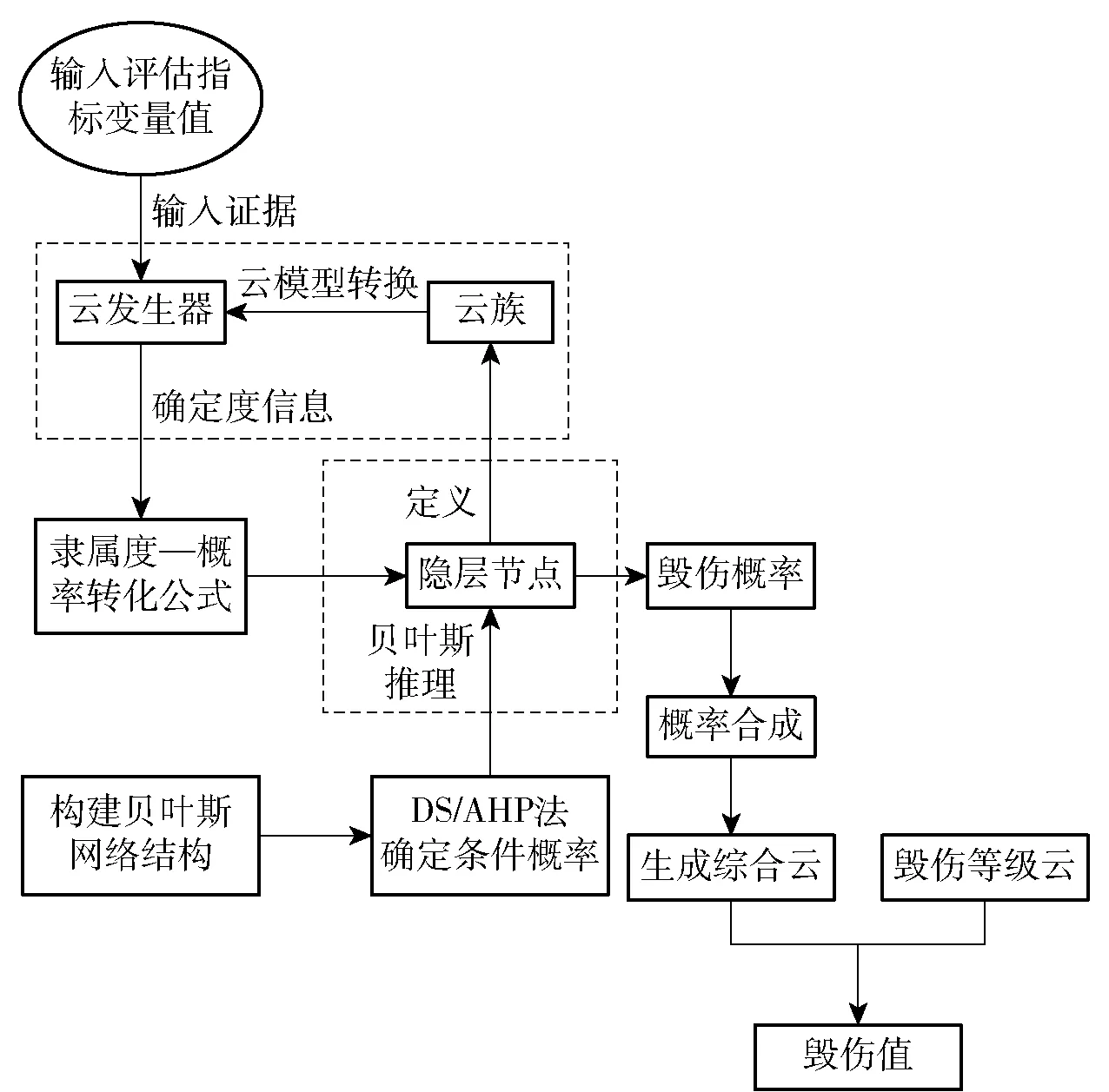
图1 云贝叶斯网络推理流程Fig.1 Reasoning process of cloudy Bayesian network
云贝叶斯网络的推理步骤如下:
1)根据作战问题背景确定贝叶斯网络结构;
2)确定评估指标体系,对指标体系内的变量进行归一化处理,定义节点云族并设计云发生器;
3)对变量进行云模型转换,得到变量对应的隶属度,比较变量对论域内不同等级状态的隶属度,依据最大判定准则,确定最大隶属度对应的隶属云即为指标对应等级状态;
4)生成目标的毁伤等级云;
5)依据DS/AHP方法确定各节点条件概率分布;
6)通过隶属度—概率转换公式将隶属度转换为概率,将节点概率代入贝叶斯网络进行推理,得到节点毁伤概率;
7)重复步骤4~步骤5,综合考虑计算时间与计算量的影响,重复计算次数不少于50次,记录各次运算结果,利用概率合成公式得到各毁伤等级概率。
2 毁伤效果评估模型的构建
2.1 构建贝叶斯网络模型
影响预警雷达毁伤程度的因素主要有干扰平台属性(干扰角度、干扰距离)、干扰时间、干扰功率、干扰频率、干扰样式、抗干扰措施、工作体制与响应机制。以上因素可归纳为干扰机攻击能力与雷达抗毁伤能力两个主要方面,其中:干扰平台属性(干扰角度、干扰距离)、干扰时间、干扰功率、干扰频率、干扰样式属于干扰机攻击能力;抗干扰措施、工作体制、响应机制属于雷达抗毁伤能力。可建立图2所示预警雷达毁伤贝叶斯网络模型。
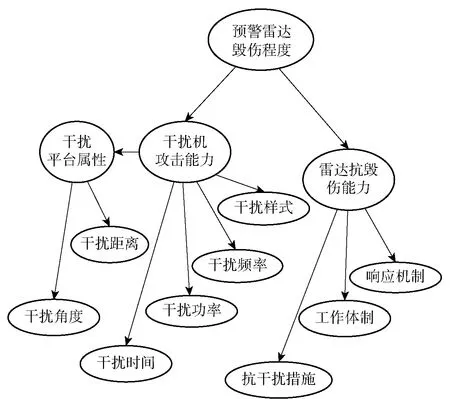
图2 预警雷达毁伤贝叶斯网络模型Fig.2 Bayesian network model of early warning radar damage
2.2 确定评估指标体系
根据图2模型,可确定评估指标体系。定义干扰机攻击能力与雷达抗毁伤能力为{很强,强,中,弱}4个状态。
2.2.1 干扰机攻击能力评估指标体系
2.2.1.1 干扰平台属性
影响干扰平台属性的因素有干扰机的角度、干扰机与预警雷达的距离。定义干扰平台属性为{很强,强,中,弱}4个状态。
设干扰机与雷达主瓣的方向角为,定义预警雷达天线接收增益- 角度系数:
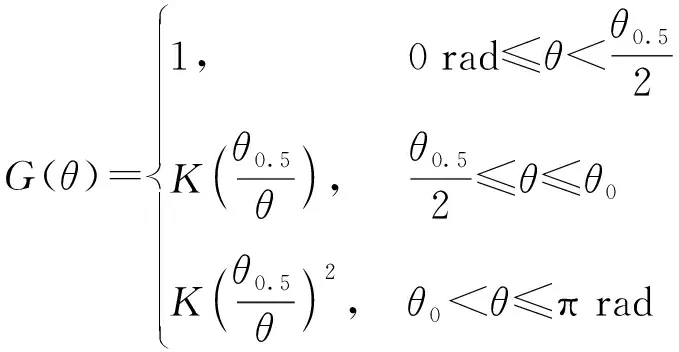
(1)
式中:为预警雷达与干扰机之间的夹角;05为预警雷达天线波瓣宽度;为增益系数,∈[002, 010]。越小,预警雷达天线接收增益就越大,干扰效果越好。定义干扰角度为{大,中,小}3个状态。
干扰机对预警雷达实施有效干扰的必要条件是二者间的距离必须大于其最小压制距离,最小压制距离越小,雷达被压制的区域越大,定义距离系数为
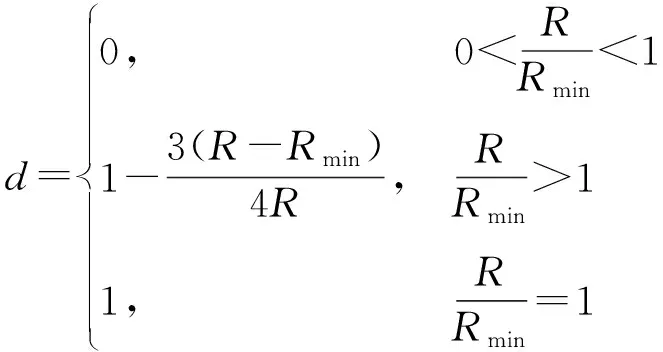
(2)
式中:为干扰平台与预警雷达之间的距离。越大,干扰效果越好。定义干扰距离为{远,中,近}3个状态。
2212 干扰时间
对预警雷达实施干扰要在一定有效的时间段内进行。设Δ表示预警雷达开机后工作时间段,Δ表示干扰机在预警雷达开机后工作时间段内实施有效干扰的时间段。定义雷达干扰时域瞄准系数为
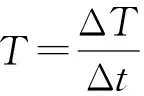
(3)
越大,干扰机在预警雷达开机后工作时间段内实施有效干扰的时间越长,干扰成功的概率越大。定义干扰时间为{长,中,短}3个状态。
2213 干扰频率
设干扰机干扰频率区间为~,预警雷达工作频率区间为~,干扰频率区间越接近雷达工作频率区间,干扰效果越好,定义雷达干扰频率覆盖系数为
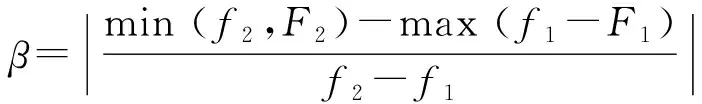
(4)
越大,干扰频率区间对预警雷达工作频率区间的覆盖能力越强,偏离预警雷达工作频率区间的程度越小,干扰效果越好。定义干扰频率为{大,中,小}3个状态。
2214 干扰功率
干扰功率越大,对预警雷达实施有效干扰的可能性越大。定义压制系数为
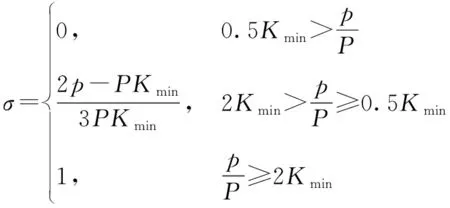
(5)
式中:为网军对预警雷达实施有效干扰时预警雷达接收机输入端需要输入的最小干扰功率;为雷达回波功率;为保证雷达正常工作所需要的最小干信比。越大,干扰效果越好。定义干扰功率为{大,中,小}3个状态。
2215 干扰样式
干扰机干扰样式越多,其与预警雷达工作体制匹配成功率越高,实施有效干扰可能性越大。设共有瞄准式干扰、阻塞式干扰、扫频式干扰与欺骗式干扰等种干扰样式,干扰机干扰样式有(≤)种,定义干扰机干扰样式系数为
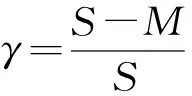
(6)
越小,干扰机对预警雷达实施有效干扰的可能性越大。定义干扰样式为{多,中,少}3个状态。
222 雷达抗毁伤能力评估指标体系
2221 工作体制
预警雷达常用工作体制如表1所示。
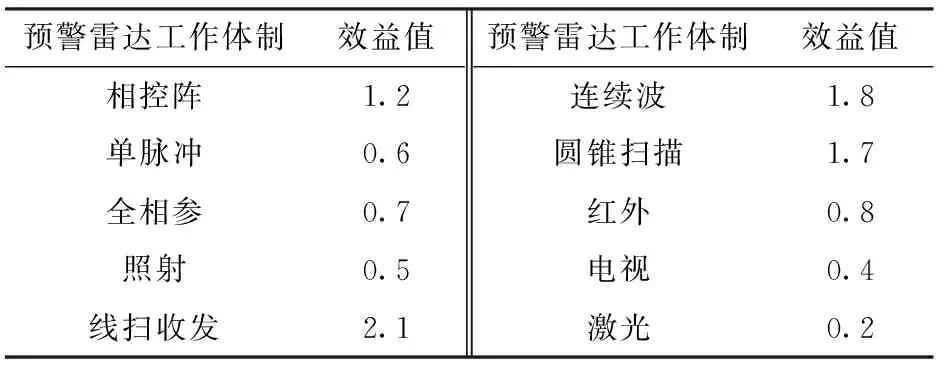
表1 预警雷达常用工作体制及效益值
定义预警雷达工作体制合成系数为
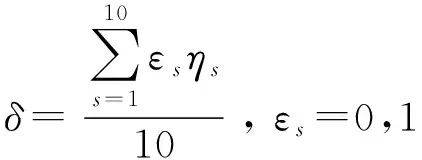
(7)
式中:为预警雷达采用第种工作体制对应的效益值,若预警雷达采用了第种工作体制,则=1,若预警雷达未采用第种工作体制,则=0。越大,预警雷达工作体制越先进,抗干扰能力越强。定义工作体制为{先进,普通,落后}3个状态。
2222 抗干扰措施
预警雷达采用的抗干扰技术措施越多,干扰机对其实施有效干扰的可能性越小。其常用的抗干扰技术措施如表2所示。
定义预警雷达工作体制合成系数ϑ为
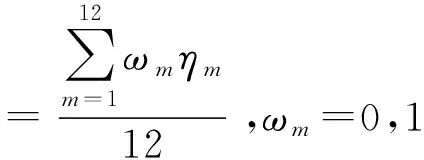
(8)
式中:为预警雷达采用第种抗干扰技术的效
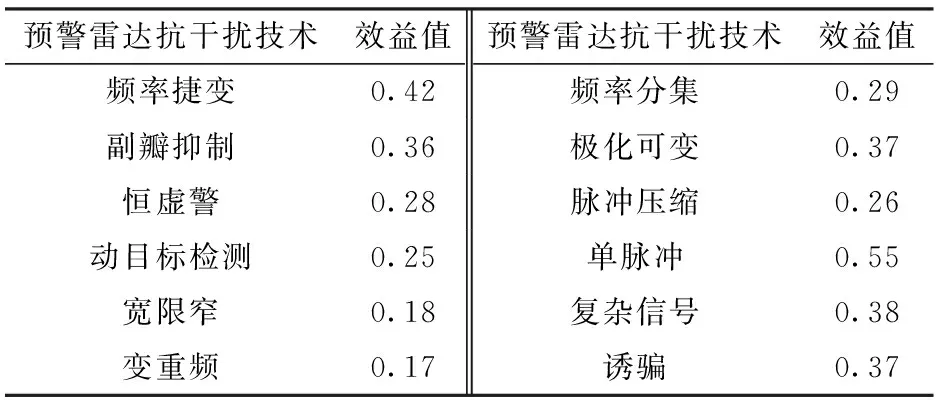
表2 预警雷达常用抗干扰技术及效益值
益值,若预警雷达采用了第种抗干扰技术,则=1,若预警雷达未采用第种抗干扰技术,则=0;为预警雷达采用的第种抗干扰措施对应的效益值。越大,预警雷达抗干扰能力越强。定义抗干扰措施为{多,中,少}3个状态。
2223 备份(接替)能力
预警雷达在自身受到打击而丧失作战能力后,通常会启动备份(接替)等响应机制,以弥补原雷达毁伤而引发的整体作战能力的下降。设预警雷达启动备份(接替)等响应机制的成功率为,定义响应概率密度函数()服从指数分布:
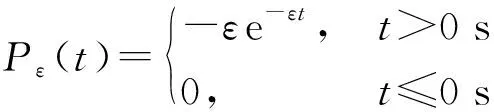
(9)
则预警雷达遭受攻击后发生故障而处于停机状态,经过时间启动备份(接替)响应机制的成功率为
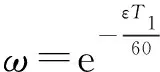
(10)
由(10)式可知,响应机制启动时间越短,响应机制启动成功率越大,预警雷达备份(接替)能力越强。定义响应机制为{快,中,慢}3个状态。
2.3 体系变量归一化处理
由于21节得到的指标体系变量的量纲与范围均不相同,为了便于评估,采用如下原则对变量进行归一化处理:
对于越大越好型指标,有
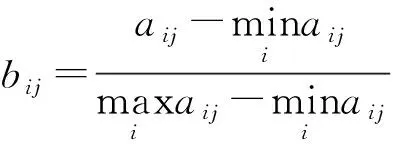
(11)
式中:为指标变量。
对于越小越好型指标,有
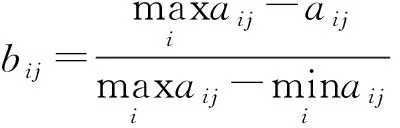
(12)
2.4 云模型转换
云模型转换即在归一化处理后的指标体系变量的论域中定义一个云族,根据云族设计相应的云发生器,将指标体系变量输入云发生器即可得到变量对应各定性概念的隶属度。
由于正态云具有很强的普适性,本文选择正态云定义云族。根据22节对各节点状态的定义,对于有3个状态的节点,在论域=[0,1]内设计云族,=(期望,熵,超熵),分别表示为云族1(1)、云族2(2)、云族3(3)。其中,云族1=(015,005,0005)、云族2=(05,005,0005)、云族3=(05,005,0005),如图3所示。
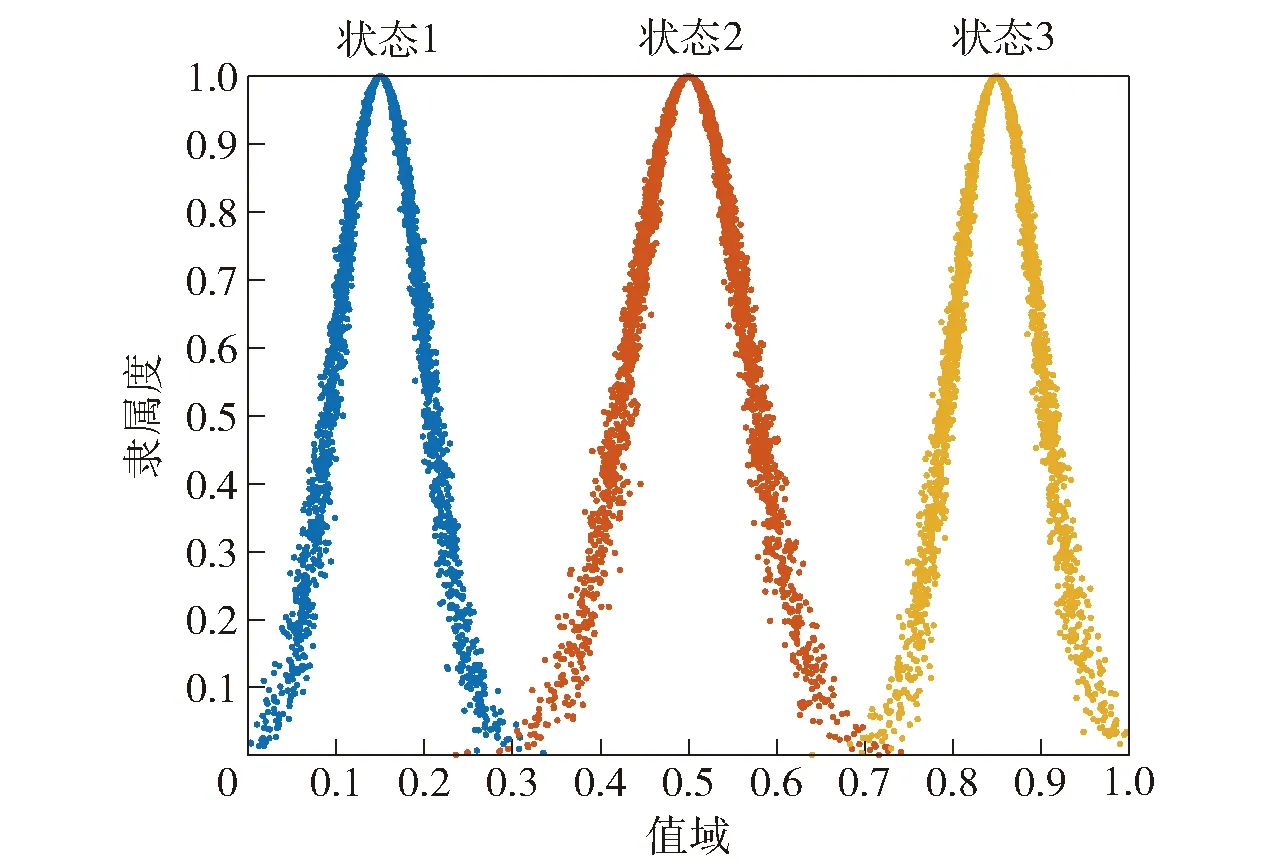
图3 有3个状态的云族Fig.3 Cloud family with 3 states
对于有4个状态的节点,在论域=[0,1]内设计4个云族,分别为1=(015,004,0004)、2=(035,004,0004)、3=(065,004,0004)、4=(09,004,0004),如图4所示。
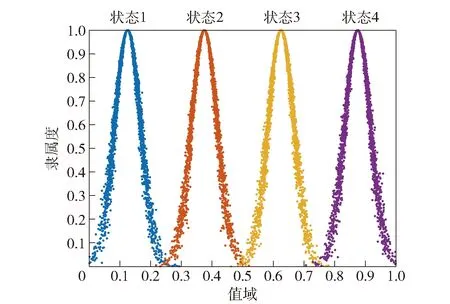
图4 有4个状态的云族Fig.4 Cloud family with 4 states
云发生器可实现定性概念与定量数据间的相互转化。正向云发生器通过输入云模型数字特征产生云滴,实现定性概念向定量数据转化,如图5所示。图5中,为期望,为熵,为超熵,(,)为云滴,为特定值,为的确定度。
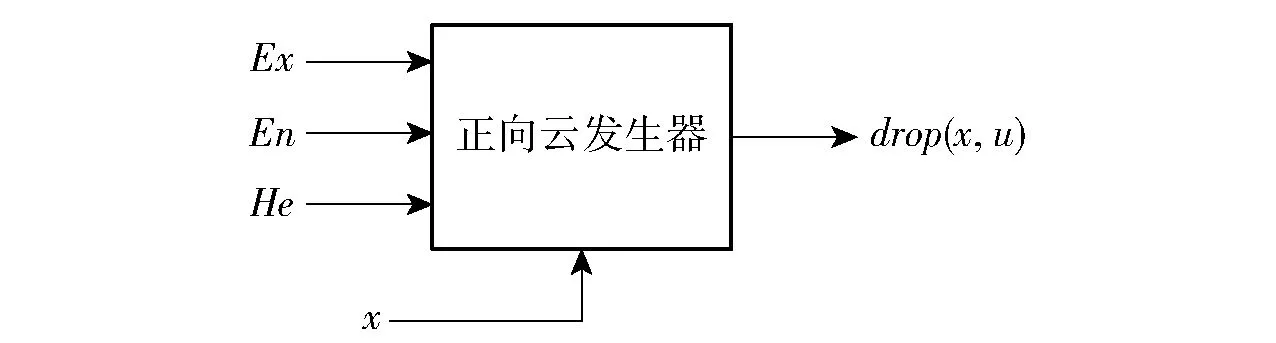
图5 正向云发生器Fig.5 Forward cloud generator
正向云发生器的算法为:
输入:定性概念的数字特征(,,),特定值;
输出:特定值对应的云滴(,)。
算法步骤为:
1) 生成一个正态随机数:1=(,)。
2)计算特定值的确定度:
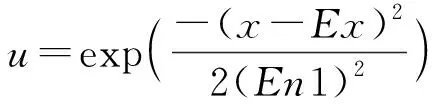
(13)
可利用隶属度- 概率转换公式将节点隶属度转换为可用于贝叶斯网络推理的概率。概率- 隶属度转换公式为
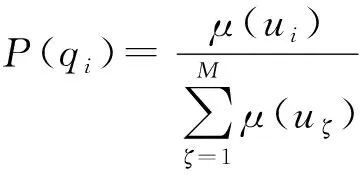
(14)
式中:为变量对论域的隶属度;为隶属度对应的值。
为消除云发生器产生云滴的不确定性影响,可经过多次推理并依据概率合成公式得到体系目标最终毁伤等级,具体步骤为:
1) 设体系目标有、、、…、共个毁伤等级,经过次推理后得到推理结果:
=[(),(),(),…,()]
(15)
2)分别合成各次推理结果,得到目标属于各毁伤等级的概率为
=[(),(),(),…,()]
(16)
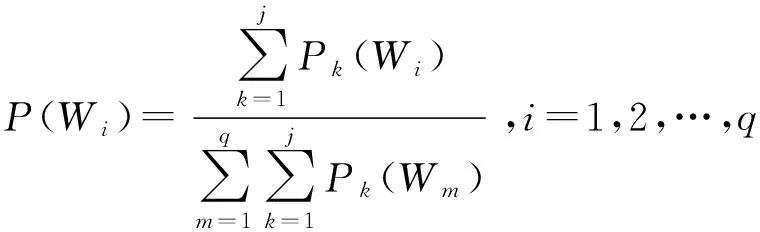
(17)
2.5 生成毁伤等级云
预警雷达毁伤程度可划分为无毁伤、轻度毁伤、中度毁伤、重度毁伤、失能5个等级,对应毁伤值如表3所示。
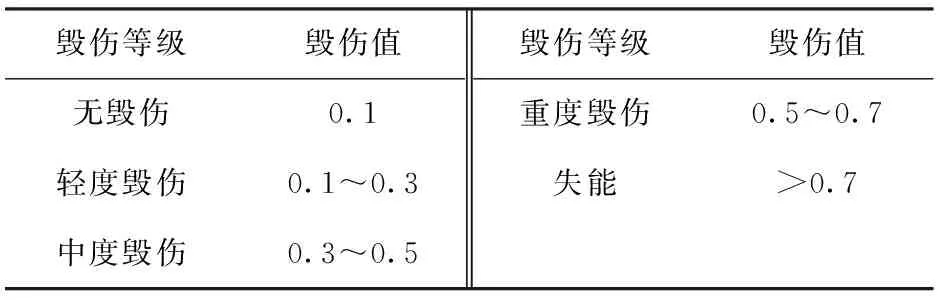
表3 预警雷达毁伤等级
根据云模型的定义,利用正向云发生器,将预警雷达各毁伤等级转化为对应的云模型,设预警雷达毁伤等级论域满足=[0,1],各毁伤等级对应的论域区间分别为:无毁伤=[0,01],轻度毁伤=[01,03],中度毁伤=[03,05],重度毁伤=[05,07],失能=[07,10]。
云模型满足正态分布,设预警雷达某毁伤区间为[,],毁伤区间云模型数字特征参数为=(+)2、=(-)6、=10。 因此,预警雷达毁伤区间对应的毁伤云数字特征如表4所示。
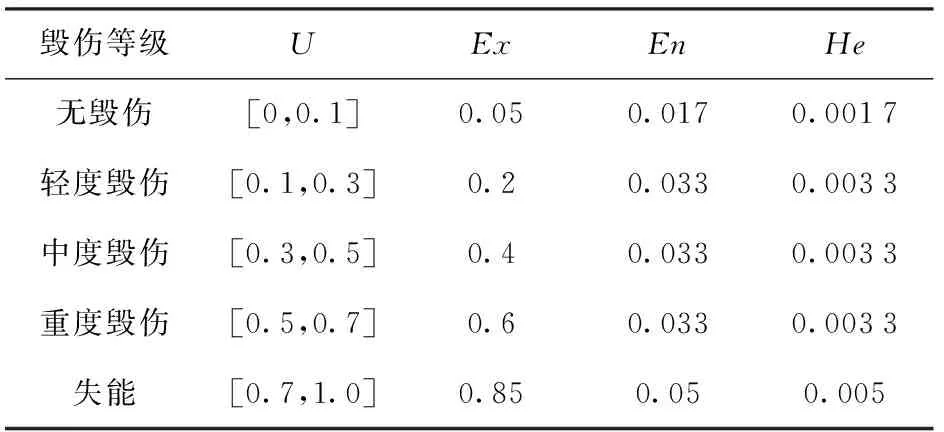
表4 预警雷达毁伤云数字特征
各毁伤等级对应云模型如图6所示。
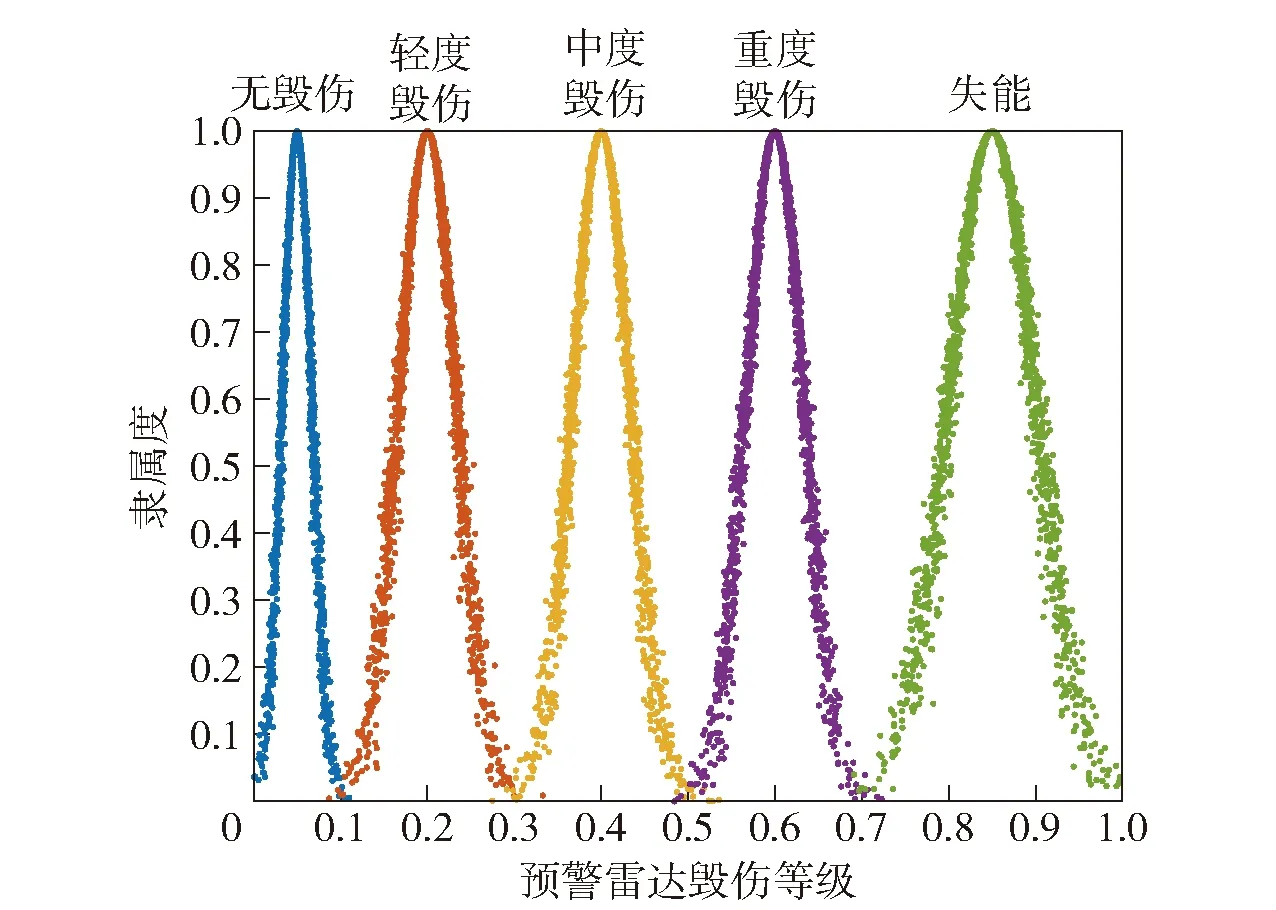
图6 预警雷达毁伤等级云模型Fig.6 Damage level cloud model of early warning radar
3 确定条件概率
实际问题中,在给定贝叶斯网络拓扑结构的前提下,确定各节点条件概率的方法主要是通过对已有数据信息进行训练得到条件概率信息。而在利用统计信息生成条件概率表时,常会出现因统计信息缺失而无法训练得到完整的条件概率表。 DS/AHP方法结合了DS与AHP法,将不完整的专家经验信息进行表达、融合,有效地降低了传统专家经验法推断结果的不确定性。专家决策判断标准如表5所示,与传统AHP法相比,DS/AHP法避免了选择方案比较与模型一致性检验等工作,专家可就熟悉的方案进行判断,对不确定的方案则可以选择放弃。

表5 专家决策判决标准
本文因各节点状态都在3个以上,因此将节点二元状态条件概率的确定方法扩展到多元状态,研究节点多元状态下条件概率的取值方法。
设表示贝叶斯网络节点的所有可能取值集合,内节点各种状态发生的可能性互斥,则为节点的识别框架。若的幂集构成了集合2,∀⊂。定义函数:2→[0,1],若满足条件:
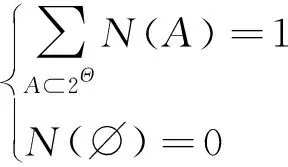
(18)
则()为上的基本信度分配函数(BPA)。根据Dempster规则,可对识别框架上两个相互独立的BPA进行合成:
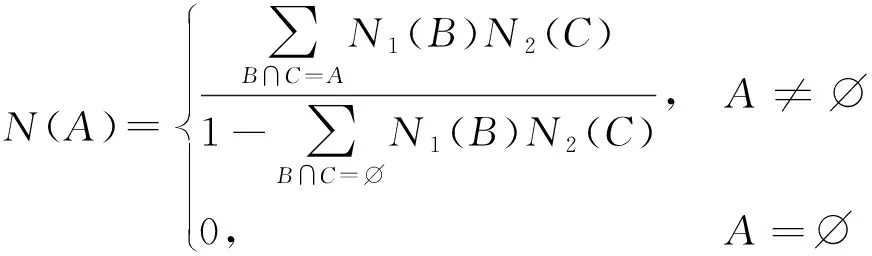
(19)
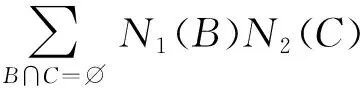
假设邀请专家参与条件概率赋值。位专家分别记为,,,…,,从维属性(,,,…,)对条件概率组合方案,,…,(∈2,=1,2,3,…,)进行相对于的重要度判断,构建基于专家评判的属性知识矩阵,如表6所示。
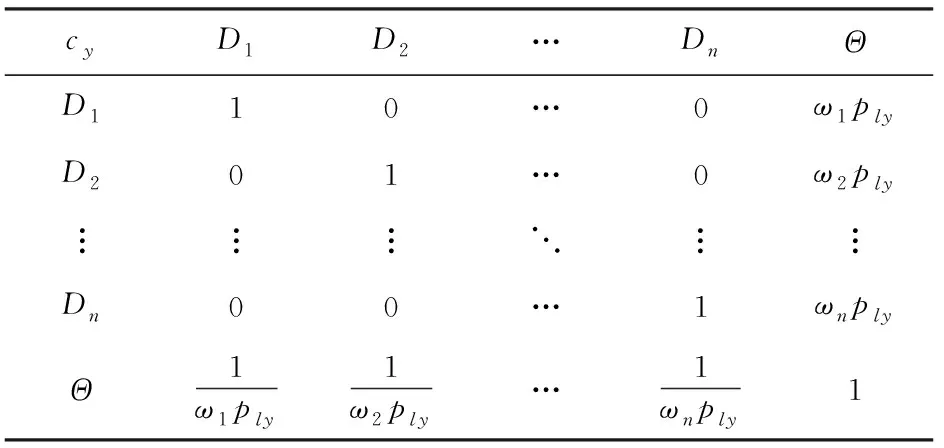
表6 基于专家el评判的属性cy知识矩阵
表6中:=1时表示方案自身进行比较,=0时表示方案未进行比较;表示属性条件下专家的权重;表示相对于的对比系数。
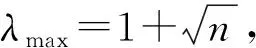
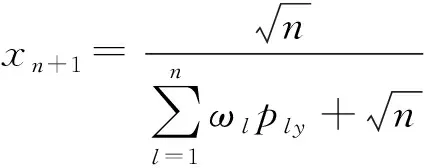
(20)
4 算例分析
我方侦测到敌反导体系的预警探测系统有4部相同型号的预警雷达,工作参数如表7所示。
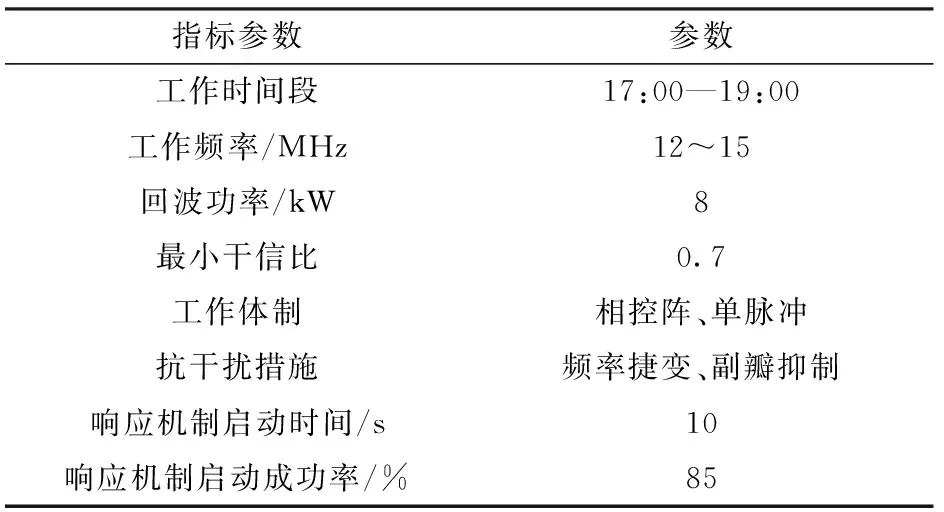
表7 预警雷达工作参数
拟对预警雷达实施干扰毁伤,共有4部干扰机,采用“一对一”模式分别对4部预警雷达实施干扰,干扰机工作参数如表8所示。
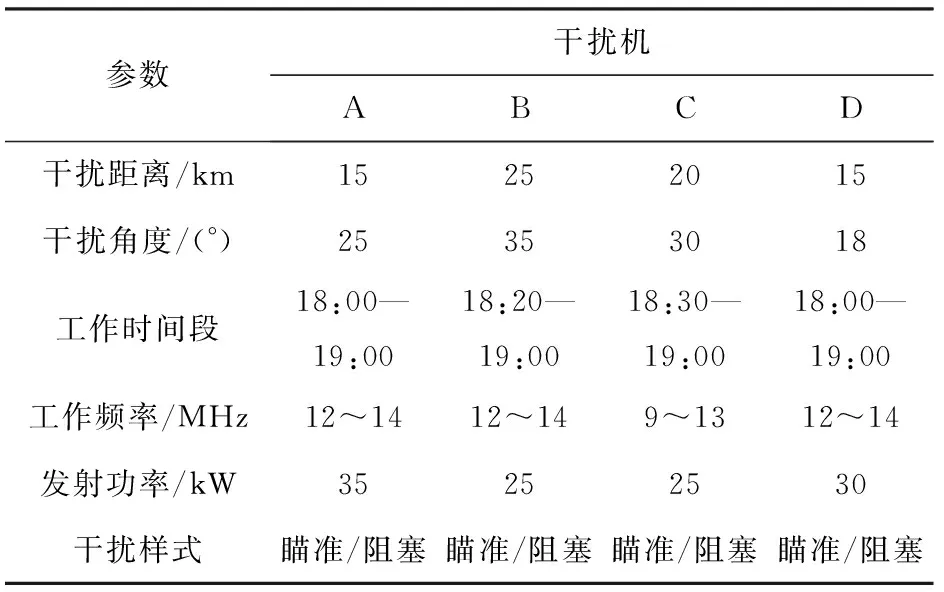
表8 干扰机工作参数
4.1 确定指标变量
结合2.2与2.3节内容,计算各评估指标体系变量并进行归一化处理,如表9所示。
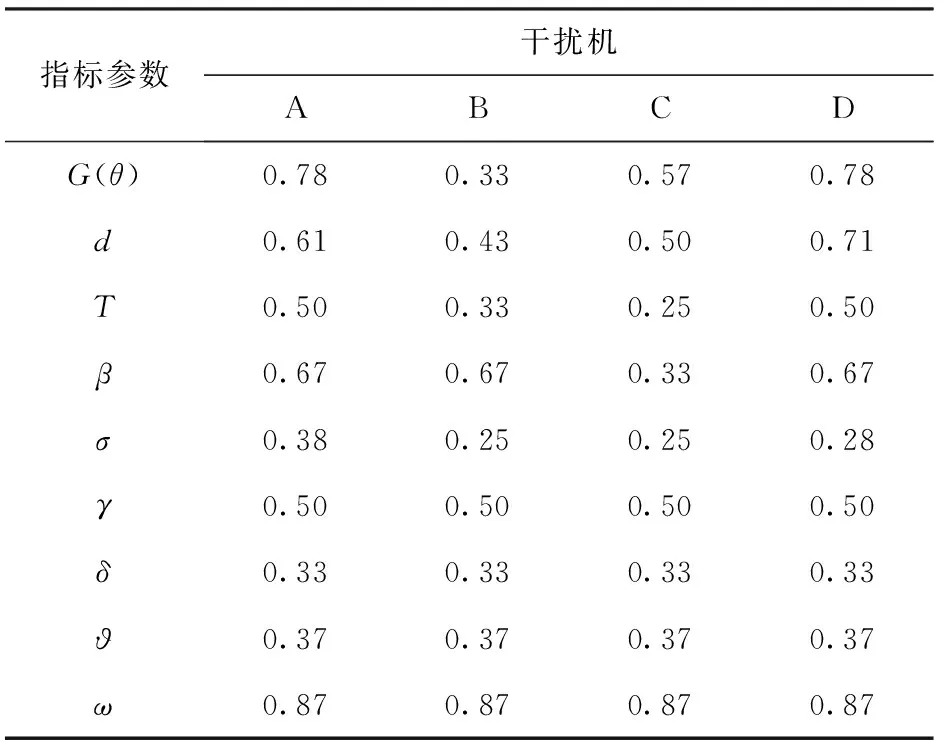
表9 归一化后的评估指标体系变量
4.2 进行推理运算
咨询4位技术专家,按照表5提供的专家决策判断标准分别计算图2中各个事件相对于子节点所处状态偏好程度的专家知识矩阵。假设参加评判工作的专家权重分别为=030、=035、=020与=015。 以预警雷达毁伤程度处于重度毁伤状态为例,建立干扰机攻击能力的专家知识矩阵,如表10~表13所示。
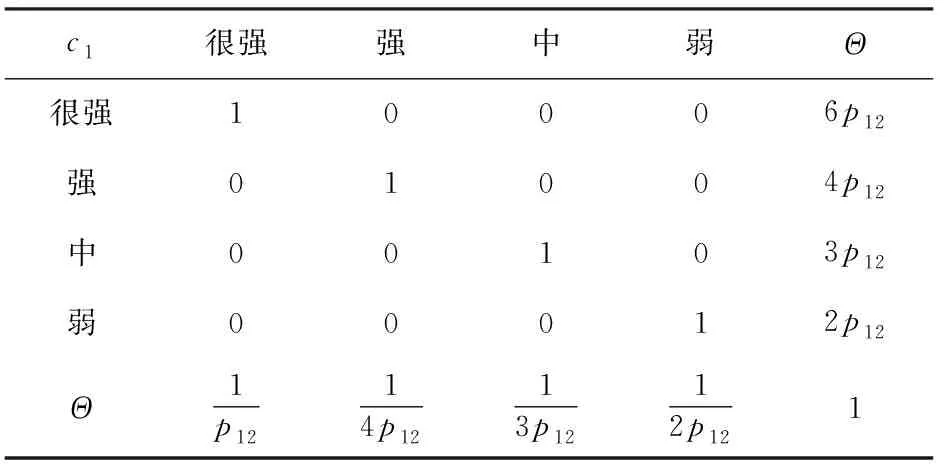
表10 以专家1偏好建立的知识矩阵B1
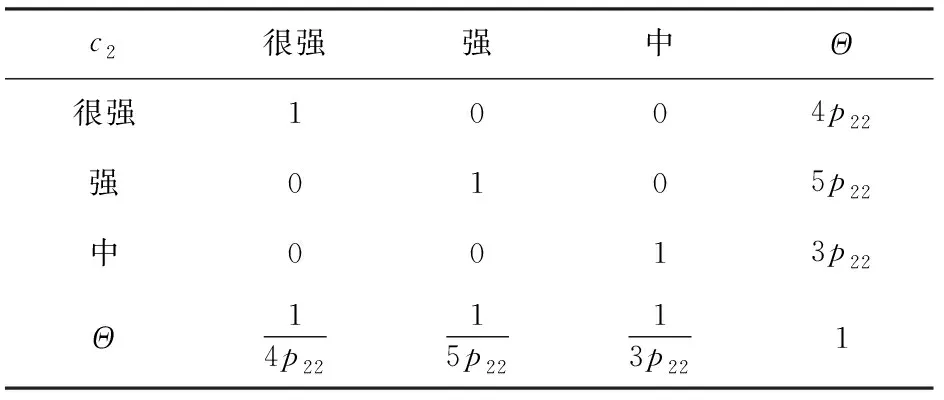
表11 以专家2偏好建立的知识矩阵B2
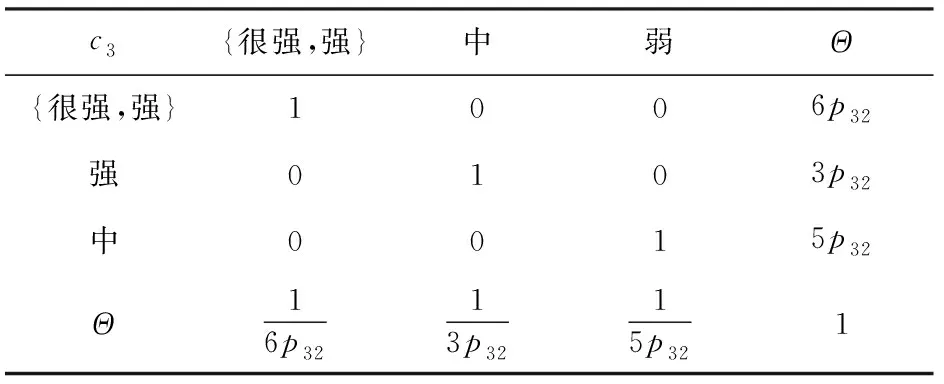
表12 以专家3偏好建立的知识矩阵B3
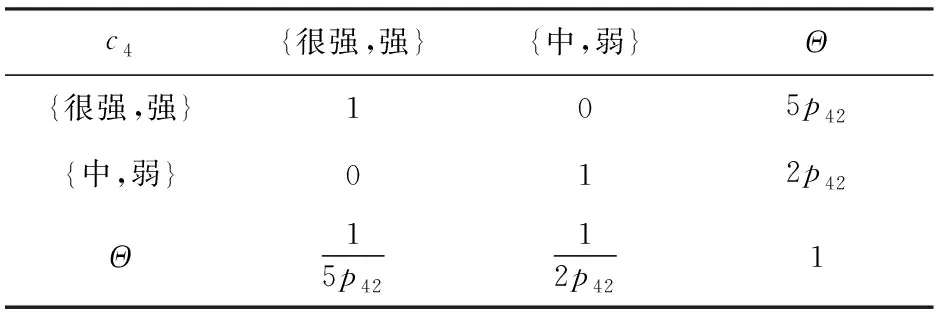
表13 以专家4偏好建立的知识矩阵B4
由(19)式与(20)式求出各证据的基本概率分配:(很强)=028,(强)=018,(中)=014,(弱)=009,()=031;(很强)=023,(强)=030,(中)=018,()=029;({很强,强})=027,(中)=013,(弱)=022,()=038;({很强,强})=({中,弱})=012,()=057。
031,按照(18)式Dempster规则,对信度函数进行合成可得事件的BPA值如表14所示。
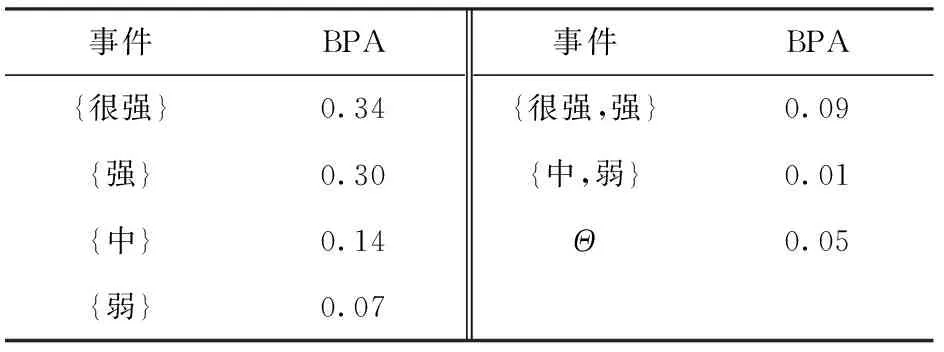
表14 信度函数合成后得到的各事件的BPA值
由表14可知,干扰机攻击能力为很强的概率为0.34+0.09/2=0.38,为强的概率为0.30+0.09/2=0.35,为中的概率为0.14+0.01/2=0.15,为弱的概率为0.07+0.01/2=0.07,不确定度为0.05。
同理,可得到其余子节点的BPA值,进而得到各子节点的条件概率值。
由于事先没有特殊说明,可假设预警雷达毁伤程度的先验概率为{0.2,0.2,0.2,0.2,0.2}。将父节点先验概率与各子节点条件概率值输入贝叶斯网络;将表8中的数据进行云模型转换后由隶属度—概率转换公式将隶属度转换为概率,以证据的形式输入贝叶斯网络。利用MATLAB软件的BNT工具箱建立如图7所示贝叶斯网络模型。
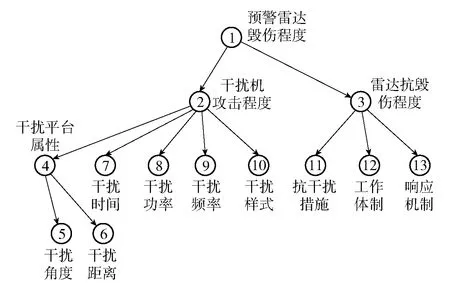
图7 BNT工具箱建立的贝叶斯网络模型Fig.7 Bayesian network model based on BNT toolbox
4.3 结果分析
初始化贝叶斯网络并通过联结树法进行贝叶斯网络推理,得到预警雷达在干扰机作用下处于不同毁伤程度的概率如表15所示,图8为各毁伤概率对应的分布直方图。
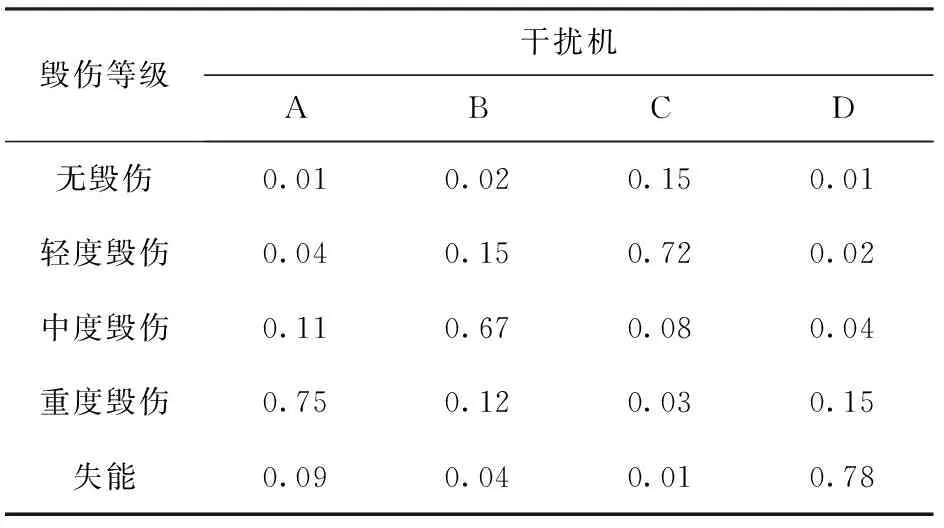
表15 预警雷达不同毁伤等级概率
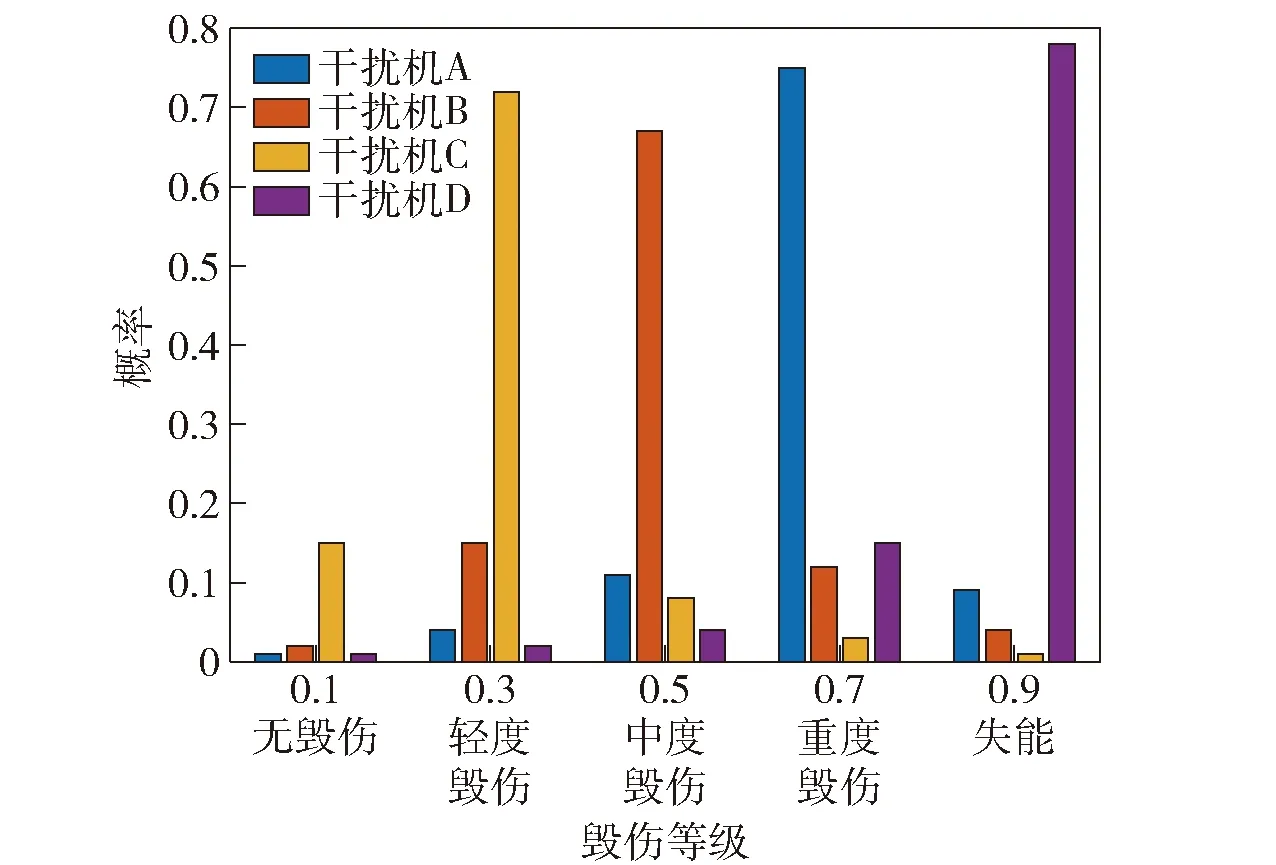
图8 各毁伤概率对应的分布直方图Fig.8 Distribution histogram of each damage probability
分析表15可知:在干扰机A攻击下,预警雷达属于重度毁伤等级的概率为0.75;在干扰机B攻击下,预警雷达属于中度毁伤等级的概率为0.67;在干扰机C攻击下,预警雷达属于轻度毁伤等级的概率为0.72;在干扰机D攻击下,预警雷达属于失能状态的毁伤等级分别为0.78。
分析表15的计算结果可知,干扰机A、干扰机D 对预警雷达的毁伤效果优于干扰机B、干扰机C,而由表8可知,干扰机A、干扰机D在干扰距离、发射功率等方面均优于干扰机B、干扰机C,这也说明了本文提出方法的计算结果与所给数据的一致性。干扰机D与干扰机A的攻击距离更接近于其最小压制距离,同时二者的干扰功率较之干扰机B与干扰机C更大,在干扰功率上更容易形成压制。
同时,干扰机A的干扰角度大于干扰机D,干扰机D的发射功率小于干扰机A,若要比较干扰机A与干扰机D对预警雷达的干扰效果,仅仅通过表8中的数据是无法做出判断的,而通过本文提出的算法可以推理得出干扰机D对预警雷达的干扰效果优于干扰机A。
虽然干扰机A的干扰功率大于干扰机D,但干扰机D的攻击角度大于干扰机A,干扰机D对预警雷达的毁伤效果更佳,可见干扰机D较之干扰机A在干扰角度方面的优势更为显著。
同理,干扰机C较之干扰机B在干扰距离、干扰角度方面有优势,但干扰机B在工作时间段、工作频率方面较之干扰机C有优势,因此,仅仅通过对比表8数据显然也无法比较干扰机B与干扰机C对预警雷达的干扰效果。
虽然干扰机C较之干扰机B在干扰距离、干扰角度等方面更有优势,但在工作时间段、工作频率方面,干扰机B的性能较之干扰机C的优势更加显著,所以干扰机B对预警雷达的毁伤程度更高。
根据推理运算,可得到各干扰机对预警雷达的毁伤效果从好到次的排序为干扰机D、干扰机A、干扰机B、干扰机C。 在实际作战中,可根据干扰机的工作参数估算对预警雷达的工作效果,以为作战分析提供可行依据。
如图9所示,可得到干扰机相对于各毁伤等级的综合毁伤云图,图9中蓝色部分对应图6云模型。干扰机A、干扰机B、干扰机C、干扰机D的毁伤值分别为0.67、0.35、0.14与0.83。通过对比相似面积分别确定干扰机A、干扰机B、干扰机C、干扰机D的毁伤等级为重度毁伤、中度毁伤、轻度毁伤与失能,与之前分析能够匹配。
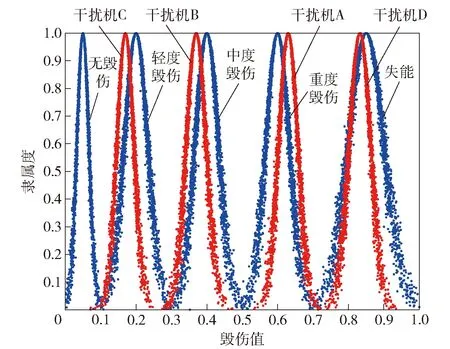
图9 综合毁伤云图Fig.9 Comprehensive damage cloud map
4.4 算法有效性分析
为验证本文方法的有效性,将贝叶斯网络法、模糊综合评判法、云重心评判法、云贝叶斯网络法用于目标毁伤效果评估,将各类评估方法所得结果与算例结果进行对比分析,结果如表16所示。
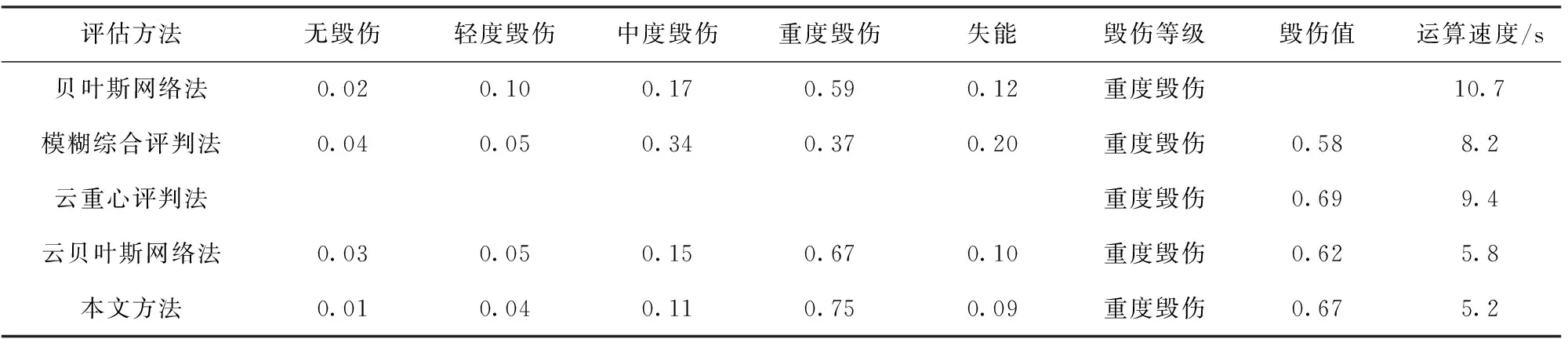
表16 各类评估方法的结果对比
由于篇幅限制,表16只列举了各类算法在预警雷达受干扰机A攻击下的运算结果。分析结果可知:
1)5种算法求得的毁伤等级均为重度毁伤,证明了本文算法的合理性。
2)贝叶斯网络法利用模糊理论实现了贝叶斯网络中节点隶属度向贝叶斯推理概率的转化,虽然得到了预警雷达属于各个毁伤等级的概率,但无法求出毁伤值。由于概率是不确定性的体现,若无毁伤值做对照,则所求结果可靠性不够。
3)模糊综合评判法求得了预警雷达属于各毁伤等级的概率与毁伤值,但由于中度毁伤与重度毁伤的概率值差别不大,故直接判定预警雷达属于重度毁伤的准确性还值得商榷。
4)云重心评判法求得的毁伤值与本文所得的毁伤值相近,但无法得到预警雷达属于各毁伤等级的概率。若不与其他毁伤等级做比较而仅凭毁伤值判断毁伤等级属于重度毁伤,则求解过程中信息的单一性将导致判断误差的增大。
5)云贝叶斯网络法求得的预警雷达毁伤等级与毁伤值均与本文算法相近,进一步印证了本文算法的合理性,但其在确定条件概率时仅依靠实验数据,若实验数据存在缺失或较大误差,则所得结果的偶然性必然增加。
6)本文方法的运算速度为5.2 s,与云贝叶斯网络法的运算速度接近,相对于贝叶斯网络法、模糊综合评判法、云重心评判法有较明显的优势。
5 结论
本文以贝叶斯网络模型为基础,通过引入云模型理论,建立了基于云贝叶斯网络的预警雷达毁伤效果评估模型,在此基础上,采用DS/AHP法确定评估模型各节点的条件概率值,推理运算得到各毁伤等级概率。得出以下主要结论:
1)本文方法得到了预警雷达属于各毁伤等级的概率值,判定了预警雷达的毁伤等级并确定了对应的毁伤值。综合而言,本文方法在计算合理性与准确度方面均优于文中提到的其他方法。
2)本文方法在运算速度上也较之其他方法具有一定的优势,运算速度分别较云贝叶斯网络法、贝叶斯网络法、模糊综合评判法、云重心评判法提升了11.5%、105.8%、57.7%、80.8%。
3)本文方法为后续研究工作明确了方向,使用的研究思路可扩展于研究不同工况下干扰机对预警雷达实施“多对一”模式干扰、“一对多”模式干扰时的毁伤效果,还可将本文研究思路推广到对其他目标毁伤的研究工作中,分析组合攻击模式下体系目标毁伤效能的变化情况。

