基于谐波频率点能量占比指标的铣刀磨损监测＊

何周杰 胡 秋 马小龙

（中国工程物理研究院机械制造工艺研究所，四川 绵阳 621900）

刀具是高端数控机床精密制造中的重点关注对象之一。一方面，刀具磨损状态直接影响工件的尺寸精度、形位精度以及表面质量。另一方面，刀具磨损还影响加工效率和加工成本，据统计机床总停机时间的20%是由刀具磨损更换所致[1]，而整个加工成本的3%～12%为刀具成本[2]。因此，有必要对刀具的磨损状态进行监测。

目前，学者们提出了众多关于刀具磨损状态监测的指标。彭锐涛等[3]通过后刀面磨损宽度指标衡量铣刀的磨损严重程度，由于采用视觉边缘检测技术，该指标只能在铣刀停转时使用。何光伟等[4]通过计算切削力（矩）分量与铣刀径向磨损的相关系数确定与刀具磨损最相关的切削力（矩）分量，然后以此指标进行铣刀磨损状态监测，该方法的缺点是在确立切削力（矩）分量时，需要不断测量刀具的径向磨损量，操作麻烦且耗时。艾长胜等[5]基于声发射信号提出线性预测倒谱系数指标以实现铣刀磨损监测，但声信号中包含电机声、切削液声等噪声，一定程度上会影响监测结果的准确性。

本文基于振动信号和二阶时间同步提取变换[6]提出用以评估铣刀磨损程度的两个指标，并利用铣削试验验证所提指标的有效性。由于振动传感器安装简单且对加工环境无特殊要求，所提指标在应用中更具有实用性。

1 指标设计思路

对于刀刃切入、切出工件所产生的冲击振动信号来说，其时频谱图中蕴藏着大量刀具磨损信息，图1展示了铣削加工时冲击振动信号的时频谱图。当在铣刀转速不变且各刀刃均无磨损的情况下，时频谱图上的脊线[7]具有明显的周期性，随着刀刃磨损加剧，其周期性逐步减弱，因此脊线的周期性规律可用来表征铣刀的磨损程度。由于时频谱图为二维信号，其周期性规律可由二维傅里叶变换得到，本文通过研究典型时频谱图二维傅里叶变换规律，提出2个铣刀磨损监测指标。

图1 铣削加工时冲击振动信号的时频谱图

2 二阶时间同步提取变换

时频谱图的获取是整个铣刀磨损状态监测的关键环节，传统的时频谱图可通过短时傅里叶变换(short-time Fourier transform，STFT)得到，但由于海森堡-加博尔不定原理[8]的制约，其时频聚集性差、噪声大，不利于后续处理。而二阶时间同步提取变换(second-order time synchroextracting transform，TSET2)

在处理冲击信号方面具有优异的性能，该方法能获得高聚集性、低噪声的时频谱图[6]，因此本文采用二阶时间同步提取变换处理采集信号。

2.1 实现流程

图2展示了二阶时间同步提取变换的实现流程：首先计算冲击振动信号的短时傅里叶变换结果（原时频平面）以及表征脊线位置的群延迟算子（群延迟平面），然后在同一频率下仅保留群延迟算子与时间标号(列标)相等的时频点上的时频系数，并将其余系数置0，最终获得高聚集性、低噪声的时频谱图（提取时频平面）。

2.2 短时傅里叶变换

短时傅里叶变换的时频结果在时域t的表达式可表示为：

式中：x(t)与h(t)分 别代表振动信号和窗函数，τ 与 υ分别表示时移变量和频移变量，*以 及j分别指代共轭符号和虚部单位。时移 τ 与 频移 υ直接构成了时频平面( τ,υ)。基于帕塞瓦尔定理，短时傅里叶变换的时频结果在频域 ω的表达式可表示为：

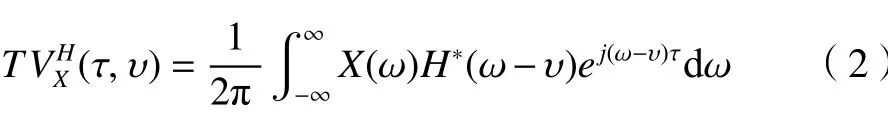
式中：X(ω) 和H(ω)分别是振动信号与窗函数的频域表达式。由式（2）可得图2中的原时频平面。

图2 二阶时间同步提取变换实现流程

2.3 群延迟算子计算

基于高斯调幅线性群延迟频域信号模型[9]，通过一系列偏微分操作可得到群延迟算子 τˆ2(τ,υ)的计算表达式：

2.4 同步提取

借助狄拉克函数 δ (·)的性质[10]，二阶时间同步提取变换TSET2( τ,υ)可定义为:

由式（4）可知，只有当τ =τˆ2(τ,υ)， 存在TSET2(τ,υ)=时频平面上的其他位置均是TSET2 (τ,υ)=0。通过式（4）可得图2中的提取时频平面。

2.5 二阶时间同步提取变换效果

图3a和图3b分别展示了图1方框区域在短时傅里叶变换和二阶时间同步提取变换下的结果。可以发现，后者具有较强的时频聚集作用，其在凸显冲击信号时频特征的同时将噪声隔离开来，从而方便基于最小二乘脊线提取方法[11]获得只包含冲击特征的时频谱图3c。后文中将脊线提取后的时频谱图作为二阶时间同步提取变换的结果。

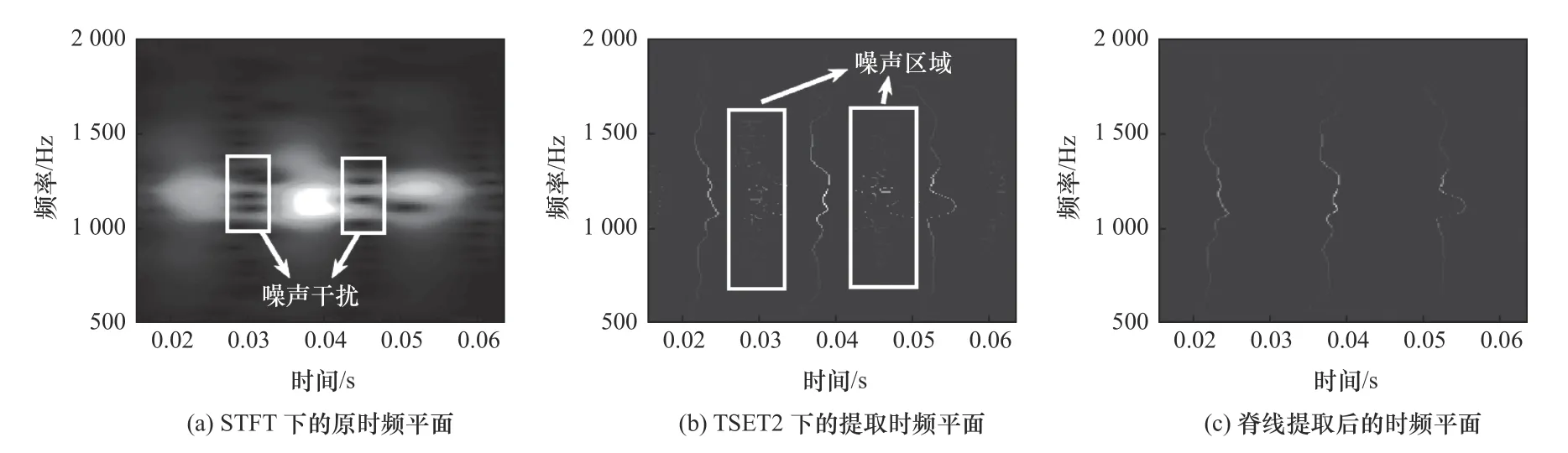
图3 刀具冲击振动信号的时频谱图

3 铣刀磨损评估指标设计

3.1 二维傅里叶变换定义

二维傅里叶变换可对二阶时间同步提取变换时频谱图的周期性规律作定量分析，其定义如下：

式中：| TSET2(τ,υ)|2表示2阶时间同步提取变换的时频谱图，u表示时移变量 τ的时移频率，其实际量纲为s，z表 示频移变量 υ的频移频率，其实际量纲为Hz。时移频率和频移频率分别反映时频谱图上脊线在时间轴方向和频率轴方向上的周期变化规律。

3.2 典型时频谱图的周期性规律

为引出刀具磨损指标，图4给出了典型的时频谱图及其二维变换结果。如图4a所示，等值分布平面上的幅值均取1，类似于一维信号中的直流偏置信号，其二维傅里叶变换结果（见图4b）仅在原点 (0,0)处存在数值，因此该点被称为“直流频率点”；如图4c所示，等间隔分布平面在沿着时移变量 τ方向上存在一系列等间隔的能量带，类似于一维信号中的周期信号，其二维傅里叶变换结果（见图4d）仅在z=0处存在一系列的能量点，这些点被称为“谐波频率点”，能量点的间隔代表等间隔分布图中能量带的出现频率；如图4e所示，非等间隔分布平面在沿着时移变量方向 τ上存在一系列非均匀分布的能量带，类似于一维信号中的非周期信号，由于无明显的周期规律，其二维傅里叶变换结果（见图4f）仅在z=0处存在能量，并且无明显的谐波频率点；如图4g所示，含噪分布是在等间隔分布基础上在时频谱图中随机添加“噪声块”，因此该分布的二维傅里叶变换结果（见图4h）除了具有图4d所示的特征外，在z= 0以外的部分存在着泄露的能量。

上述讨论为铣刀磨损评估指标的提出带来启发。对于无磨损的铣刀，其时频谱图类似于图4c，当出现磨损后，由于刀刃缺口的不均匀性，其时频谱图类似于图4e，它们的二维傅里叶变换结果的能量均只出现在z=0直线上，唯一差别是出现磨损后，部分能量泄露至谐波频率点以外，因此可通过谐波频率点在z=0上的能量占比评估铣刀的磨损情况，其中谐波频率点的位置可以通过主轴转频与铣刀齿数的乘积计算得到。由图4a及图4b可知，直流频率点属于特殊的谐波频率点，但由于不能体现冲击信号的周期性规律，因此在铣刀磨损评估时需要排除在外，由图4g及图4h可知，测量过程中产生的噪声会使得部分能量泄露至z=0的直线之外，从而降低铣刀磨损评估的灵敏度，因此需要采用高聚集性、低噪声的二阶时间同步提取变换时频谱图作为输入来进行分析。

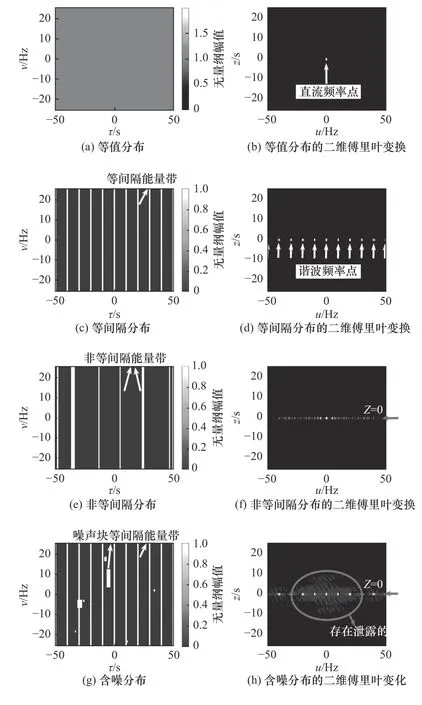
图4 典型的时频谱图及其二维傅里叶变换结果

3.3 指标定义

假设铣刀转频为fr， 铣刀有 z0齿，则冲击频率可表达为fp=fr·z0， 而谐波频率点可表示为fi=i·fp,i∈{i∈Z|-fs/2≤fi＜fs/2} ， 其中fs为信号采样率。本文把i=0的 谐波频率点称为“直流频率点”，把i=±1的谐波频率点称为“主谐波频率点”。由此可定义两个衡量铣刀磨损情况的量化指标，其一是描述除直流频率点以外的谐波频率点能量集中程度的谐波频率点能量占比指标Rf：

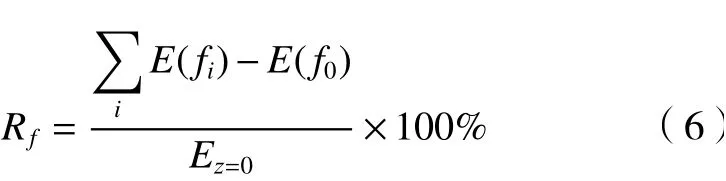
式中：E(fi)代 表谐波频率点fi处 的能量数值，Ez=0表示在z=0直线上的能量总和。

由于冲击频率等于主谐波频率点处的时移频率，主谐波频率点可直接反映冲击信号时频谱图在时移变量 τ方向上的周期性规律，因此另一个指标可定义为主谐波频率点能量占比指标Rf±1：

根据二维傅里叶变换的性质，存在E(f-1)=E(f1)，因此主谐波频率点能量占比指标还可表示为：

上述2个指标数值越小，表明刀具磨损越严重。

4 铣刀磨损试验

4.1 试验流程

图5展示了铣刀磨损评估的一般流程。首先通过振动传感器采集铣刀加工过程中的原始时域信号，然后基于二阶同步提取变换获得高聚集性、低噪声的时频谱图，再对该时频谱图进行二维傅里叶变换，得到冲击特征的周期性规律，最后通过所提出的2个磨损指标完成铣刀磨损情况的评估。

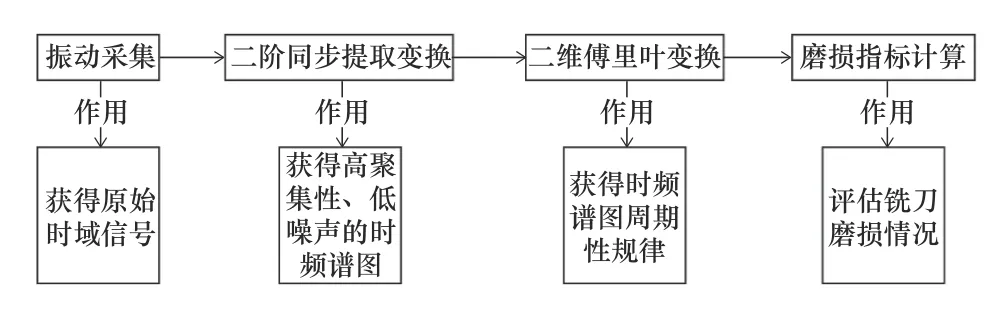
图5 铣刀磨损评估的一般流程

4.2 试验条件

为了验证所提指标的有效性，利用3把磨损状态不同T45四刃铣刀加工块状钢材质工件进行试验验证，如图6所示，工件置于测力仪基座之上，在其侧壁贴有加速度传感器，并将采样频率设置为51 200 Hz，铣刀轨迹采用“回”字形路径，加工时轴向切深为1 mm，径向切深为0.5 mm，每齿进给为0.02 mm/tooth，主轴转速为1 000 r/min。

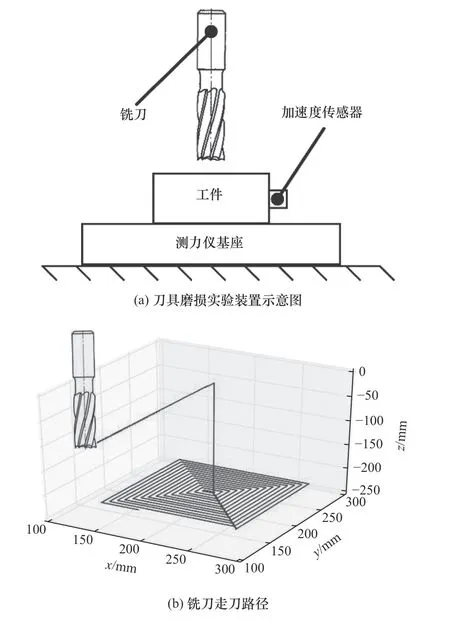
图6 铣刀磨损试验装置示意图及铣刀走刀路径

图7展示了3种磨损状态不同的铣刀，从左至右分别是#1无磨损刀具、#2轻微磨损刀具和#3严重磨损刀具，图中第1行是刀具的端面示意图，第2行是刀具的侧视图，第3行是侧视图中方框区域的局部放大图，箭头指示了刀具磨损区域。通过对比可以发现，严重磨损刀具的磨损缺口明显大于轻微磨损刀具的磨损缺口。

图7 不同磨损状态铣刀的显微镜照片

4.3 数据处理

图8展示了3把铣刀加工时所产生的振动信号及其二阶同步提取变换结果，由试验条件可知，理论的冲击频率为66.67 Hz，从试验数据中截取0.15 s长的时间片段进行二阶同步提取变换分析。

对无磨损的 #1铣刀，其各刀刃的切削状态相同，所产生的冲击特征相似且等间隔分布（如图8b所示），对存在磨损的 #2、#3铣刀，其各刀刃切削振动响应存在差别，从而导致所产生的脊线不再随时间均匀分布（如图8d、图8e所示），且随着磨损程度加剧，对应时频谱图中的脊线分布周期性规律依次减弱。为进一步量化评估，对3把铣刀的二阶同步提取变换时频谱图进行二维傅里叶变换，其结果如图9所示，其中用小圆圈标记出谐波频率点的位置，对比可以发现，磨损越严重的刀具其谐波频率点之外泄露的能量越多。

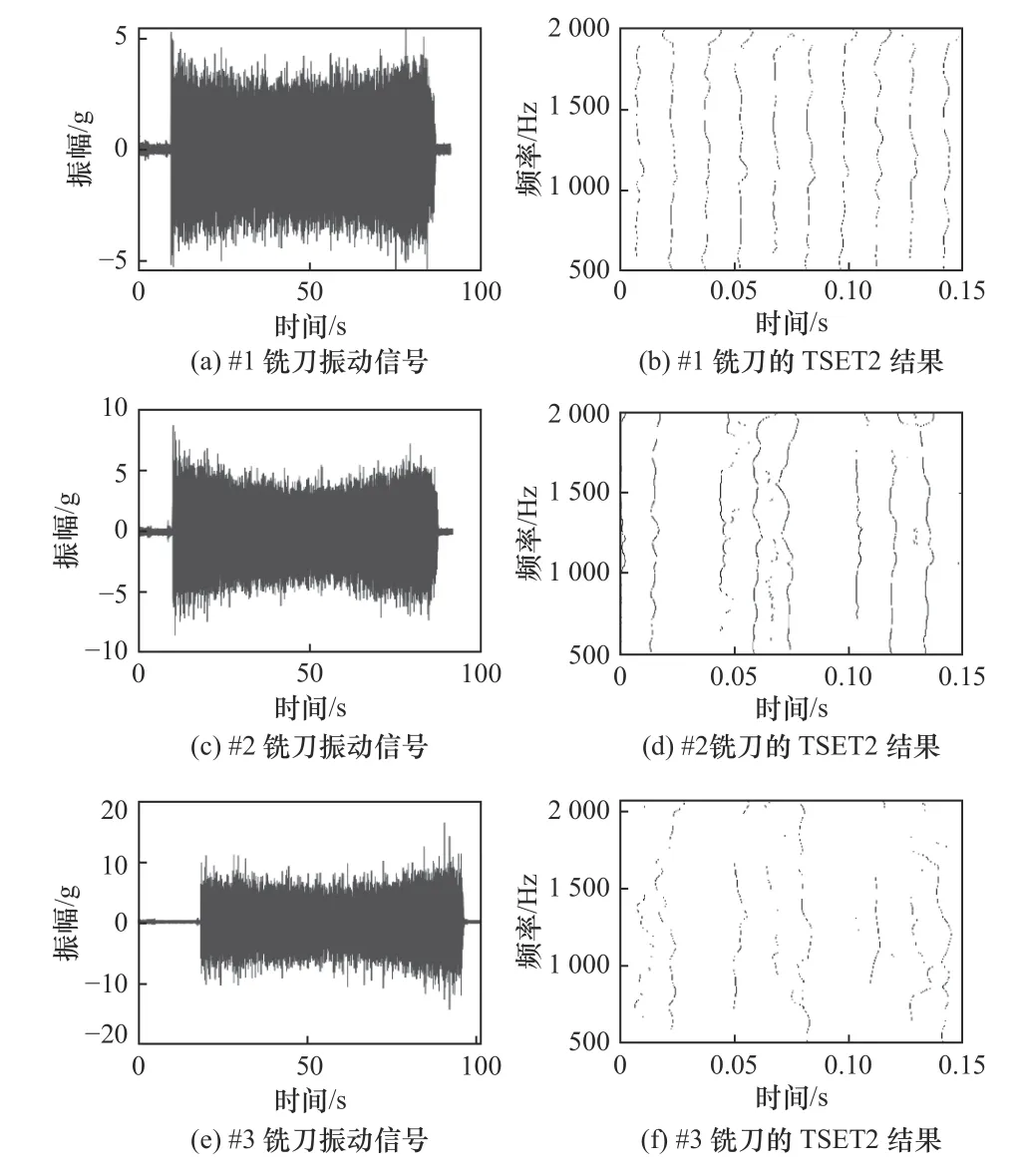
图8 3把磨损状态不同的铣刀振动信号及其二阶同步提取变换结果

图9 磨损状况不同的铣刀的二维傅里叶变换结果

基于式(6)和(8)，可以分别得到3把铣刀的谐波频率点能量占比指标以及主谐波频率点能量占比指标，其计算结果如表1所示。计算结果表明，两个指标结果均满足 #1刀具＞# 2刀具＞#3刀具，说明#3刀具磨损最严重，其后依次是 #2刀具、#1刀具，这与刀具在显微镜中所观察到的实际磨损情况一致，进而验证所提指标的有效性，因此所提指标可应用于铣刀磨损的状态监测中。

表1 谐波频率点能量占比指标和主谐波频率点能量占比指标结果

5 结语

本文基于二阶同步提取变换的时频谱图提出了用以衡量铣刀磨损状态的谐波频率点能量占比指标以及主谐波频率点能量占比指标，并用利用3把磨损状态不同的铣刀验证所提指标的有效性。

试验结果表明，所提指标的评定结果与在显微镜观察到的铣刀刀刃实际磨损情况相符，因此利用谐波频率点能量占比指标以及主谐波频率点能量占比指标可实现对铣刀磨损程度的状态监测。