锥形转子磁力耦合器调速机理研究＊

葛研军 刘述良 王建帅

（大连交通大学机械工程学院，辽宁 大连116028）

我国工业用电约占全国总电量的65%以上[1]，其中用于拖动风机、泵类设备的电机用电量分别占全国总用电量的10%和20%[2]。由于风机、泵类负载的轴功率与其转速的三次方成正比，即转速降低时，轴功率将呈三次方下降[3-4]，所以对其进行调速是目前实现风机、泵类等离心式负载系统节能的最佳方式。

调速型磁力耦合器（简称磁耦）通过永磁体磁场和导体感生磁场相互耦合来实现转速和转矩的传递，具有结构紧凑、无泄漏污染、无级调速、软启动及过载保护等特点[5-6]，在风机、泵类设备应用时可实现很好的节能效果。

现有的调速型磁耦可分为筒式和盘式两种。盘式磁耦是通过调整永磁转子和导体转子之间的气隙来实现转速及转矩的调节，由于气隙磁导为无穷大，因此通过轴向移动对其调速精度控制较难，调速区间不够明确。筒式磁耦通过改变永磁转子和导体转子之间的耦合面积进行调速，虽然其调速范围较大，但调速时轴向距离长，调速效率较低。为解决磁耦的上述问题，本文提出了一种锥形转子磁力耦合器（conical rotor magnetic coupler，CRMC）。CRMC的内、外转子及气隙均呈锥形，当转子之间的轴向距离稍作变动时，其气隙长度及相互耦合的轴向面积均发生变化，因此在具有较大调速范围的同时，其需改变的轴向长度很短，调速效率也很高。

1 模型分析与计算

1.1 CRMC结构及其工作原理

图1为CRMC机械结构简图。

图1 CRMC机械结构

图1中，CRMC由永磁转子、导体转子及气隙构成；其中，永磁转子由内轭铁及镶嵌在其上磁极交错排布的永磁体组成；导体转子由导体及外轭铁组成。

图2为CRMC工作状态示意图。其中，图2a为其额定工作状态，图2b为其调速状态。

图2 CRMC工作原理

图2a中，当导体转子旋转时，导体切割永磁转子磁场并形成感应电流，进而产生感应磁场，与永磁体磁场相互耦合使永磁转子以一定的转差开始旋转。图2b中，当导体转子与永磁转子发生轴向位移时，其轴向耦合长度减小，同时气隙长度增大，在此双向作用下，CRMC耦合磁通迅速减小，使其输出的电磁转矩及转速迅速下降，从而实现高效调速。

1.2 电磁转矩计算

筒式磁耦和盘式磁耦的磁感线分别沿径向和轴向穿过气隙，而CRMC则沿图3所示的锥面的法线方向分布。为便于气隙磁密分析与计算，可将图3等效为图4所示的盘式及筒式磁耦模型。

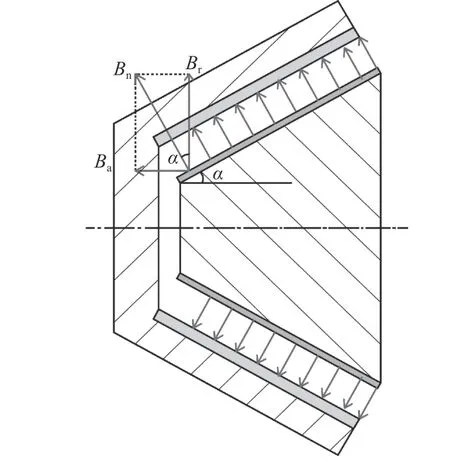
图3 CRMC磁感线分布

图4 CRMC磁感线等效模型

1.2.1 筒式磁耦电磁转矩计算

图5为图4中筒式磁耦的径向磁路展开图。由图5可知，CRMC径向主磁路为永磁体N极磁力线经内轭铁、气隙并与导体及外轭铁交链后，再经导体层、气隙回到永磁体S极；CRMC的漏磁通路径为永磁体仅经气隙但未与导体及外轭铁相匝链的闭合回路。

图5 筒式磁耦径向磁路展开

图6为图5所示的等效磁路图。图6中，Favg为永磁体平均磁动势，Φ0为总磁通，Φ1为回路主磁通，Φ2为回路漏磁通；R1、R2、R3、R4、R5和R6分别为筒式磁耦的外轭铁磁阻、铜层磁阻、气隙磁阻、永磁体磁阻、内轭铁磁阻和漏磁阻。

图6 CRMC等效磁路

由基尔霍夫定律可得图6所示的CRMC磁通与磁动势关系。

将式(1)代入式(2)可得

将图4所示的筒式磁耦由圆心位置到外轭铁最大径向尺寸处进行分层处理，可得图7所示筒式磁耦的磁阻分层结构。

由图7及磁阻计算公式可得外轭铁磁阻、铜层磁阻、气隙磁阻、永磁体磁阻及内轭铁磁阻分别为：

将图7所示模型简化可得图8所示的筒式磁耦漏磁阻结构。

图7 筒式磁耦磁阻分层结构

图8 筒式磁耦漏磁阻结构

对图8所示的漏磁阻沿径向积分可得筒式磁耦的漏磁阻

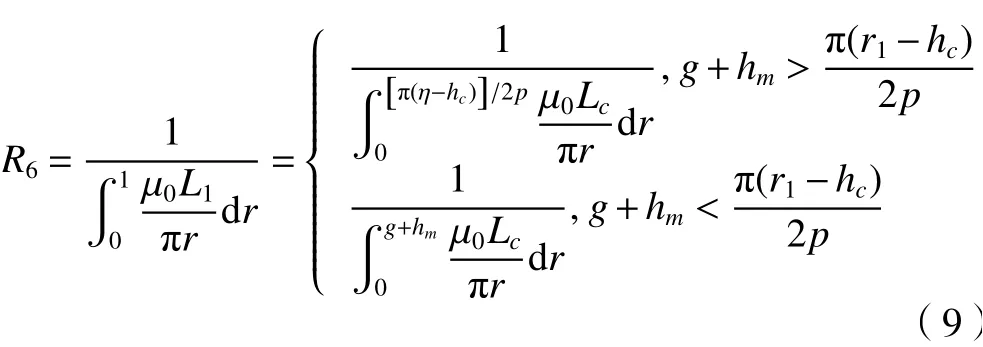
式（4）～（9）中：L为内、外转子耦合长度， μ0为真空磁导率， μ1为 外轭铁层相对磁导率， μ2为铜层相对磁导率， μ4为 永磁体相对磁导率， μ5为内轭铁层相对磁导率，S为截面积，Lc为漏磁阻N极发出的磁力线回到S极形成回路的距离。

单个永磁体的磁动势可表示为

式(10)中：Hc为永磁体的矫顽力。将式（4）～（10）代入到式（3）求出Φ0并根据Mohammadi模型可得筒式磁耦的电磁转矩T1为

式（11）～（12）中：Rco=r1、Rci=r1-hc，分别表示铜层外径、铜层内径；σ为铜层电导率，L为轴向耦合长度，s为 转差率，nin为输入转速， αm为极弧系数，p为永磁体极对数。

由式（11）及式（12）可知，T1仅与CRMC的轴向耦合长度L、转差s及输入转速nin有关，因此式（11）可写为

式（13）中，

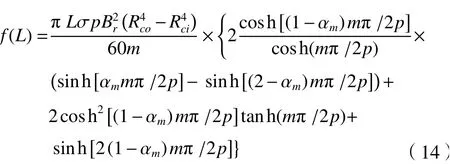
由式（13）及式（14）可知，电磁转矩T1为轴向耦合长度及转差的函数，当L及s越小时，其所传递的电磁转矩也越小；反之，则越大。

1.2.2 盘式磁耦电磁转矩计算

与筒式磁耦相同，同样采用等效磁路法，可求出盘式磁耦各层材料的磁阻及气隙磁通等参数，并

根据磁密计算公式得到盘式磁耦的电磁转矩T2为式（15）中：m=μ0σvhc/2(g+hc)， 为自定义参数，l为永磁体的长度，r0为 永磁体平均半径，Ba为盘式磁耦静态下气隙磁密，且有：

式中：φa为盘式磁耦静态气隙磁通。

1.3 CRMC轴向磁拉力计算

CRMC的轴向磁拉力为永磁转子磁场与导体转子感生磁场的相互作用力。

设E1、E2分别为转子位移前后的气隙磁场能量；Hz1、Hz2为位移前后气隙磁场强度沿极距分布的均方根值；Z表示沿轴线方向的位移量，则有

式（17）及式（18）中： ΔV1、ΔV2分别为CRMC位移前与移动后的气隙体积， τx为圆周方向极距。

由于任何电磁机械做功均由气隙及导磁体内的磁场能量变化完成，因此CRMC的轴向力F可表示为

将式（20）代入到式（19）可得

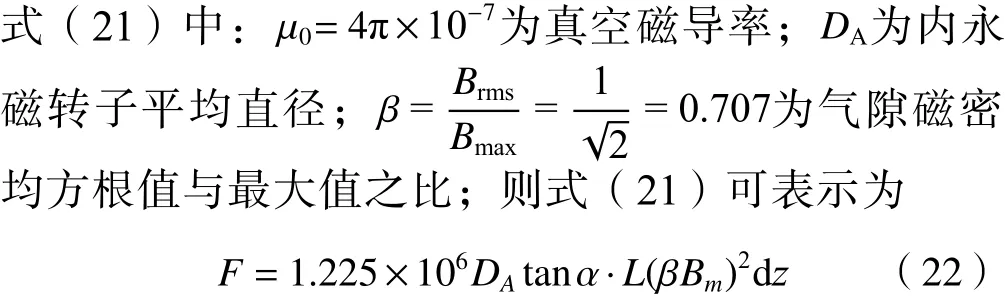
式（22）中：L为CRMC轴向耦合长度；α为单边锥角。

2 CRMC机械特性分析

2.1 运行特性分析

运行特性系指CRMC保持其完全耦合状态时由式（11）所得出的电磁转矩T与转差率s的函数关系。

图9为由式（11）所得的函数曲线。图9中，a为启动状态点；b为最大转矩点；c为同步转速点。

由图9可知：当CRMC位于a点时，转差率s为1，此时外转子静止；当T≥Tc时，CRMC可实现带载启动。启动后，CRMC的转差s迅速减小，T则呈先增大后减小趋势，且在b点处达到最大值Tmax。当s进一步减小时，T也进一步减小，当CRMC运行至c点时，转差s=0，T=0，因此c点也可称为同步点。

图9中b点为CRMC由启动状态过渡到额定状态的拐点，此点附近的转差s稍有变化时T将发生很大变化，因此该点附近为不稳定工作区，其所对应的s称为临界转差sm。

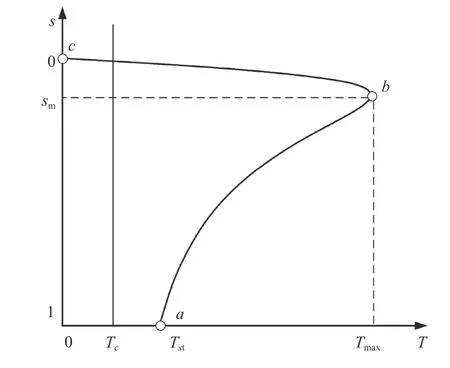
图9 CRMC机械特性曲线

图9中的c点处内、外转子转速相同，此时外转子无法切割磁力线，不能产生感生电流及感生磁场，使CRMC无法正常工作，即CRMC具有异步性。

2.2 调速关系分析

调速关系系指磁耦的轴向耦合（或气隙）长度与输出转速或转差率的关系。其在CRMC中皆有体现。当CRMC接入离心式负载时，负载转矩Tload与输出转速的平方成正比关系，即

式(15)中：k为离心式负载系数。将式(15)代入到式(13) 并由转差计算公式可得

式（24）中的L与g呈负相关性，即L=C0/g（C0为常数）。对式（24）进行离散化计算可以得到CRMC对离心式负载调速，输入转速为1 500 r/min时nout随L和g的曲线变化图，如图10所示。

图10 调速关系曲线图

CRMC内、外转子由完全啮合状态到逐渐脱离的过程中，随着L的减小和g的增大，nout整体呈现出不断减小的趋势。L由100 mm减小至80 mm变化的过程中，由于永磁转子的磁通量保持较大值，使得CRMC有效地维持在稳定状态，所以nout基本没有变化。L由80 mm减小至60 mm的变化过程中，L不断减小，g不断增大，导致径、轴向磁通同时减小，因此该阶段nout呈较大幅度降低。在L由60 mm逐渐减小到0 mm的过程中，径、轴向磁通变化趋于平稳，nout呈线性下降直至为0。

3 模型仿真

3.1 CRMC三维模型建立

为验证CRMC调速关系及运行特性，基于图1及表1所示模型结构对其进行有限元仿真。

表1 CRMC结构参数

表1中，输入转速nin为1 500 r/min，永磁体材料为N40SH，导体材料为紫铜T2。

3.2 启动与运行特性分析

由图11为CRMC启动与运行特性曲线。

图11 启动与运行特性曲线

由图11知，可将CRMC运行状态划分为启动、调整及稳定运行等3个阶段。

(1)当t∈[0,130] 时为启动阶段，该阶段的内、外转子转差较大，导体层中的感应电流、电磁转矩及涡流损耗也较大；该阶段中的最大扭矩值为860 N·m （约为额定转矩的4倍），最大损耗值达到46 kW；该阶段内永磁转子获得的转矩冲量较大，可使其迅速增加至额定转速（1 480 r/min）附近。

(2)当t∈（130,170] 时为调整阶段，该阶段内、外转子转差相对上一阶段有所减小，转矩冲量在此阶段达到峰值，并使输出转速出现大于输入转速现象 （即所谓的超调状态）；经超调波动后，内转子转速及转矩缓慢降低并收敛于稳定状态，损耗也逐渐减小并趋于稳定。

(3)当t∈（170,+∞）时为稳定运行阶段，该阶段内、外转子的转速、转矩及损耗皆为额定值（转速为1 480 r/min，转矩为25 N·m，损耗为1 kW），且曲线的波动值较小，传递效率较高（约为 9 8.7%），满足CRMC稳定运行要求。

3.3 调速特性分析

图12为CRMC在轴向耦合长度分别为100 mm、60 mm及30 mm时的调速特性曲线。

图12中，曲线1的轴向耦合长度为30 mm，曲线2为60 mm，曲线3为100 mm（完全耦合），曲线4为离心式负载的运行特性曲线。

由图12可知，离心式负载特性曲线4与曲线1、曲线2和曲线3分别相交于点a、 点b及 点c，所对应的横、纵坐标值分别为CRMC在调速过程中的转矩及转速，各交点与横、纵坐标轴所围成的面积即为CRMC的输出功率。

图12 CRMC调速特性曲线图

当CRMC在完全耦合状态下运行时，曲线3与曲线4所对应点c的转速、转矩及功率分别为1 480 r/min、235 N·m及36.4 kW。

改变CRMC的轴向耦合长度分别为60 mm及30 mm时，CRMC的输出转速、转矩及功率将随之减小；其中，点b所对应的转速、转矩及功率分别为908 r/min、87 N·m及8.2 kW；点a分别为381 r/min、15 N·m及0.6 kW。

由上述计算结果可知，点c为CRMC运行效率最高点，该点也称为额定工作点；点b与 点a的转矩及输出功率与点c的对应值均呈平方及立方关系下降，满足离心式负载的相似性关系。

图13为CRMC逐渐减小耦合长度时由完全耦合至完全脱离时所得的输出转速、转矩及损耗变化曲线。

图13 CRMC调速关系曲线图

由图13可知，CRMC由完全耦合（100 mm）减小到80 mm时，转速及转矩均减小缓慢，说明CRMC有20 mm（约20%）的轴向余量。

当耦合长度由80 mm减小至62 mm时，由于法向磁通迅速减小，内、外转子转差迅速增大，此过程中，转速及转矩分别降低30%及50%，涡流损耗在62 mm，转差为1/3时达到峰值5.4 kW。

当耦合长度由62 mm进一步减小至0 mm（完全脱离状态）时，磁通量减小趋于平稳，转速呈线性下降，转矩呈平方倍下降，损耗也由峰值状态迅速降低到零。

3.4 CRMC轴向力分析

CRMC的轴向力包括永磁体沿锥面法向对外轭铁的吸力及导体层的感应磁场与永磁体磁场相互耦合形成的斥力。轴向力关系着调速机构的设计及轴承选型，直接决定着调速过程的难易程度[7]。

图14为不同耦合长度的轴向力与转差的关系曲线。图14中，正值为吸力，负值为斥力。

图14 不同耦合长度轴向力-转差率曲线

由图14可知：（1）当转差率s≤0.2时，完全耦合状态下的CRMC轴向力为吸力且随着s的增大而减小；其他耦合长度下的轴向力则为斥力，且随s的 增大而增大。（2）当转差率s＞0.2时，所有耦合长度状态下CRMC的轴向力均趋于稳定；其中，完全耦合状态下的轴向力趋近于0；其他耦合状态下的轴向力则随耦合长度的减小而减小。（3）耦合长度80 mm和60 mm的轴向力基本相同，这是因为耦合长度为60 mm时，CRMC的感生涡流达到极值，其和永磁体磁场耦合所产生的斥力也增大为与80 mm的耦合长度相当。

4 结语

（1）CRMC电磁转矩T与气隙磁密B的平方呈正比，因此B对其具有较大的正相关性；又由于T与转差率s也成正比，因此CRMC具有良好的调速特性。

（2）与筒式和盘式磁力耦合器相比，由于CRMC的锥角特性，调速时气隙长度及轴向耦合磁通均发生较快变化，使其具有较高的调速效率。

（3）CRMC的缺点是其轴向力较大，且轴向力与内、外转子直径，轴向耦合长度，单边锥角以及最大气隙磁密幅值有关。