GNSS高程拟合在高原基础测绘中的应用研究

梁双凤

(甘肃省测绘工程院，甘肃兰州 730000 )

1 引 言

我国西部高原地区资源丰富，盛产天然气、煤炭、石油以及地方特色土特产品。为了将这些资源和特产运送出来，实现国家西部大开发战略，国家做出了很多战略部署。基础测绘是战略部署中非常重要的环节，但高原地区地形复杂，自然环境恶劣，人迹罕至，有广袤的沙漠百里风沙区，也有荒无人烟的戈壁滩“无人区”，给高原基础测绘工作带来了巨大的挑战，特别是实施水准测量非常困难。据有关报道，测绘生产单位开展的高原基础测绘相关航空摄影测量内外业工作，包括构建测量 C级GNSS网、布测像控点及像片外业调绘等，但水准测量几乎无法实施。GNSS测量得到的是大地高，而工程项目采用正常高程系统，因此，GNSS测量的大地高需要通过大地水准模型转换为正常高，才能用于工程项目。基础测绘航空摄影高程基准的高程精度要求较高，为了解决高原基础测绘高程基准测量困难的问题，需要一种更高效的获取高精度像控点高程值的方法。

国内外学者对GNSS高程转换理论和实践进行了大量的探索和研究[1]。高伟[2]通过大量GNSS高程拟合理论与实践研究，精化了似大地水准面，其高程精度可达±2 cm。根据参考文献[3]，深圳市似大地水准面精化模型的高程异常的绝对精度达±1.4 cm。随着数学与计算机技术的快速发展，地球重力场模型提出后，国内外学者又提出了很多新方法、新模型来解决高程拟合问题[4-5]。本文主要针对高原地区高程基准难以解决的实际工程问题，探索一种适用于高原地区的GNSS高程拟合方法，解决高原基础测绘像控点高程基准问题。利用GNSS测量像控点平面坐标得到精确大地高数据，结合测区少量已知公共点数据，通过高程拟合方法，解算出大量像控点的高精度高程异常值，进而计算得到这些像控点的高程值。经文献研究发现，曲面拟合方法和“移去—恢复”法具有较高精度。因此，本文基于这两种方法，利用MATLAB平台自编程序，构建多种拟合模型，并结合高原基础测绘项目实例，得到适合高原基础测绘的最佳高程拟合模型。本研究成果可以为高原基础测绘以及其他相关测绘在高效解决高程基准的问题上提供参考。

2 GNSS高程拟合算法

2.1 多项式曲面拟合模型

当测区范围较大时，可采用多项式曲面拟合模型，通过已知点高程异常解算模型中的系数，然后计算待定点的高程异常，根据高程异常与正常高的关系计算待定点的高程值。该算法步骤如下[6]：

1)建立多项式曲面方程，如公式(1)所示。根据已知点的坐标(x,y)和高程异常值ξ，求解多项式曲面函数的系数。

(1)

式中：ai为多项式曲面函数的系数，εi为高程异常残差值。

2)根据步骤1)中求得的系数，将待求点坐标代入多项式函数，解算出未知点的ξ，用该点的GNSS观测的大地高，可求出该点的正常高的高程值。

多项式曲面拟合模型具有多种形式，根据公式(1)选用项的不同，可得不同的曲面拟合模型[7]：

1)当选用式(1)中的前三项时，建立的拟合模型为平面拟合模型，该模型仅需3个已知点高程异常值，就可以解算方程系数。该模型适用于平缓地区，但在地形复杂地区精度不高。

2)当选用式(1)中前三项和第五项进行拟合时，可构建相关平面拟合模型，解算模型系数需要至少4个已知点高程异常值。该模型仍是用平面代替附近高程异常值，适用于地势平坦地区。

3)利用式(1)中前六项进行拟合，所得到的数学模型是二次曲面拟合模型，模型系数求解需要6个已知点高程异常值，能够较好地拟合具有起伏变化的地形信息。

4)利用式(1)中所有项进行拟合得到的数学模型为三次曲面拟合模型，模型较为复杂，需要至少10个已知点高程异常值，方可进行求解系数。该模型对于较复杂的地形有很好的模拟效果。

已知高程点的个数，通常会多于模型所需要的数据个数，此时应按最小二乘法平差方法，求解模型系数的最佳估值。

2.2 “移去—恢复”法高程拟合模型

李建成院士等诸多学者对我国似大地水准面精化的理论和方法研究做出了巨大贡献，研究发现重力场模型能够提高GNSS的高程拟合精度，因此提出了“移去—恢复”法的高程异常拟合模型，在GNSS高程拟合中得到了广泛的应用[8]。

根据地球重力场的可叠加性，将高程异常分解为3个分量：

ξ=ξGM+ξΔG+ξT

(2)

式中：ξGM表示地球重力场中高程异常的长波分量，ξΔG表示用斯托克斯积分得到的高程异常的中波分量，ξT表示地形起伏变化引起的高程异常的短波分量。3个分量的关系如图1所示。

图1 高程异常3个分量关系示意图Fig.1 Schematic diagram of the relationship among three components of elevation anomaly

在一定范围内高程异常的中、长波分量相对稳定且变化小；而短波分量则受局部地形影响，小范围内也存在较大差异。因此，首先需要将高程异常中的中、长波分量移去，然后对剩余的短波分量进行拟合和插值计算，从待求点的短波分量中拟合高程异常值，最后再恢复待定点中、长波分量。该方法可以有效地避免拟合和插值计算过程导致中、长波分量的计算损失，进而提高高程拟合的精度。模型计算基本步骤如下[9-10]：

1)移去：首先求出n个已知点的高程异常值，用重力场模型计算各点的中、长波高程异常分量，然后计算高程异常的短波分量，即得到高程异常值与中、长波分量的差值。

2)拟合：根据n个已知点的坐标和短波分量值，利用MATLAB建立多种数学拟合模型，求解待求点的高程异常值短波分量的拟合和插值。

3)恢复：利用步骤2)中求解的高程异常短波分量，与步骤1)中求解的中、长波分量进行代数运算，即可得到待求点的高程异常值的拟合值。

2.3 GNSS高程拟合精度分析

GNSS高程拟合精度通常需要根据内符合精度、外符合精度和相关水准等级精度要求进行评定。

1)内符合精度。为了检验GNSS高程拟合的精度，利用已知高程异常值点与拟合高程异常值求残差Vi，然后求其内符合精度σ。

(3)

(4)

2)外符合精度。GNSS高程异常拟合精度还可用水准实测方法来检核，根据水准测量结果求得高程异常值，再与拟合高程异常值计算残差Vout，然后利用公式(4)计算得到外符合精度。

3)GNSS高程拟合精度评定。精度评定通常按照常规几何水准测量的精度评定方法，根据公共点、检核点、待求点之间构建的水准网，设已知检核点至公共点的距离L(km)，再根据国家水准测量规范进行公式计算和等级评定。

表1 水准限差技术要求Tab.1 Levelingtolerancetechnicalrequirements等级允许残差/mm三等水准测量±12L四等水准测量±20L五等水准测量±30L

3 工程算例

3.1 工程概况

试验区为某高原基础测绘项目，项目主要包括GNSS控制测量C级网及航空摄影测量外业工作。测区东西长约165 km，南北宽约60 km，基础测绘航空摄影测量设计为1∶10 000地形图264幅(其中卫星影像成图157幅，航摄像片成图107幅)。区域内布设C级GNSS观测点61个，其中检核点25个(采用二、三等水准测量)，像控点158个(待测高程点)。C级GNSS控制测量，二、三等水准测量，像控点平面坐标测量均按国家相应规范进行测量。

3.2 多项式曲面拟合模型

根据多项式曲面拟合模型函数，自编MATLAB程序分别建立平面拟合、相关平面拟合、二次曲面拟合、三次曲面拟合4种拟合模型。利用已知点的数据得出各模型的拟合系数，再将像控点的大地坐标代入该模型，解算出各像控点的高程异常。根据检测点的高程异常值和拟合计算得到的高程异常值，计算残差，再根据外符合精度进行精度估算，并统计出各检测点的残差，结果如图2所示。

图2 多项式曲面法拟合残差分布曲线Fig.2 Residual distribution curve of polynomial surface fitting

根据残差分布曲线可得，平面拟合、相关平面拟合模型的残差较大，而二次曲面拟合、三次曲面拟合模型残差较小，三次曲面拟合方法总体趋势优于其他拟合模型，误差分布在(-0.4 mm，0.8 mm)范围。为了进一步分析模型质量，对检核点高程异常的残差进行统计分析，结果如表2所示。

表2 高程异常的多项式曲面拟合残差统计Tab.2 Statisticsofpolynomialsurfacefittingresidualsofelevationanomalies类别平面拟合模型/mm相关平面拟合模型/mm二次曲面拟合模型/mm三次曲面拟合模型/mm最大值0.7130.7720.3730.289最小值0.0160.0080.0330.006中误差0.4810.5110.2280.181

根据表2分析，上述4种拟合方法中，平面拟合法与相关平面拟合法的中误差较大，分别为0.481 m和0.511 m。而二次曲面拟合与三次曲面拟合方法较前两种方法的精度有较大提升，分别为0.228 m和0.181 m。因此，三次曲面函数模型拟合效果最好。

3.3 “移去—恢复”拟合模型

根据EGM2008地球重力场模型，将所有公共点作为已知点，得到中、长波高程异常分量。利用“移去—恢复”算法，解算像控点高程异常，并进行精度分析。将公共点坐标转换为经纬度，再利用AllTrans EGM2008 Calculator计算EGM2008地球重力场模型的高程异常。将已知点高程异常的中、长波移除后，采用自编MATLAB程序构建曲面拟合、多面函数拟合以及移动曲面拟合3种模型，并分析模拟结果，最后利用同样的原理计算外符合精度。4种模型的残差分布结果如图3所示。

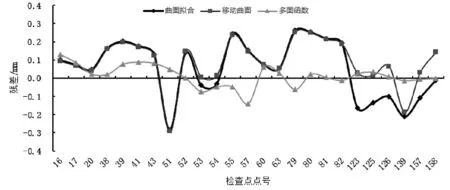
图3 “移去—恢复”法拟合残差分布曲线Fig.3 Residual distribution curve fitted by “remove-restore”method

从图3可以看出，曲面拟合方法与移动曲面拟合方法稍差，多面函数法的总体外符合精度最好。但是总体来看，“移去—恢复”模型的精度要高于多项式曲面模型，误差分布在(-0.3 mm，0.3 mm)范围。“移去—恢复”模型的残差统计结果如表3所示。

表3 “移去—恢复”模型中误差统计Tab.3 Theresidualstatisticsof“remove restore”model类 别曲面拟合/mm移动曲面/mm多面函数/mm最大值0.2850.2920.141最小值0.0110.0060.000中误差0.1660.1560.061

基于“移去—恢复”的三种拟合方法中，曲线拟合与移动曲面方法的中误差分别为0.166 mm和0.156 mm，而多面函数方法的精度最好，中误差为0.061 mm。

通过本试验区的数据分析发现，高原基础测绘高程基准可采用高程拟合方法求解。通过对相对精度较高的集中模型进行分析，发现“移去—恢复”拟合模型中多面函数方法精度最优，且该方法的高程拟合精度能够满足高原基础测绘像控点的高程精度要求。

4 结束语

利用MATLAB自编程序，结合高原基础测绘项目，研究了GNSS高程拟合的多种拟合方法。本文利用少量公共点的GNSS高程值和高程异常值，通过高程拟合方法解算出像控点的高程值。结果表明，在高原地形复杂的地区，使用多面函数法的“移去—恢复”模型，可得到较高精度的GNSS拟合效果，精度最高可达到6 cm。高程拟合方法可为高原基础测绘4D产品提供较高精度的高程基准，并为高原测绘相关工作提供一种高程基准测量的新方法。随着数学和计算机技术的发展，高程拟合的算法会进一步优化，使其工作量更小，精度更高，更好地为高原测绘工作服务。