转捩过程对旋翼悬停模拟的影响分析与研究

庞超, 李猛, 高正红

(西北工业大学 航空学院, 陕西 西安 710072)

旋翼作为直升机类飞行器的主要气动部件,其气动性能直接决定了整个飞行器的飞行性能。悬停和前飞是旋翼2个典型的工作状态,其中悬停性能(例如悬停效率,FoM)可以作为评价旋翼气动性能的一个关键指标。随着计算机算力的快速增长,直接从NS方程(空气动力学中“第一性原理”)出发的计算流体力学(CFD)方法逐步被用在旋翼非定常流场的模拟中。朱正、卢丛玲等[1-2]利用运动嵌套网格方法,采用BL湍流模型及SA湍流模型对共轴刚性双旋翼非定常悬停流场进行了模拟,分析了其流动干扰机理。张震宇等[3]利用多块结构化滑移网格,采用k-ωSST两方程湍流模型对刚性旋翼大前进比前飞状态进行了模拟。美国航天航空学会(AIAA)自从2014年起每年召开一次旋翼悬停预测工作组会议(AIAA rotorcraft hover prediction workshop,HPW),相继提供了3个旋翼标模[4-7]及相关的试验数据作为统一的研究对象,包括S-76旋翼、PSP旋翼和HVAB旋翼。其中针对S-76旋翼[8-9]的讨论主要集中在全湍流假设下,而HVAB旋翼模型目前缺乏正式的试验数据作为支撑。PSP旋翼是当前HPW会议中唯一有桨叶表面试验数据的计算标模,从2018年起国外研究人员开始对其进行初步的数值模拟研究[10]。在基于RANS方程的CFD方法中,转捩模拟是非常重要的一部分,CFD2030愿景[11]以及HPW愿景中均将边界层的转捩模拟作为重要的研究内容。对于固定翼类飞行器的二维、三维、高速、低速转捩模拟已经有相对成熟的方法和应用[12],然而这些转捩模拟方法在旋翼模拟中的应用却比较少见。其原因在于：一方面相比于固定翼模拟,旋翼模拟需要更大的计算代价,因为涉及非定常计算、尾迹捕捉等;另一方面转捩模拟对计算网格尺度和网格量的要求要远高于全湍流模拟。对于固定翼飞行器而言,在一些状态下,其气动、流场特性受到转捩过程的影响，会有比较大的变化,所以对于这类飞行器在设计、评估过程中必须考虑转捩的影响。而对于旋翼来说,人们需要明确是否也存在湍流模拟和转捩模拟结果差异大这一现象,以确定在设计、评估过程中采用合适的模型和计算网格。

本文采用基于嵌套网格的自研RANS求解器,对HPW提供的PSP旋翼标模进行了悬停流场的全湍流和转捩模拟,并从积分气动力、桨叶表面压力分布、桨叶载荷分布、桨叶表面流线、尾迹流场等方面详细对比讨论了全湍流模拟与转捩模拟的差异,为设计人员在评估时提供依据。同时也进一步验证了自研求解器在转捩模拟和旋翼模拟方面的可靠性。

1 数值方法

1.1 RANS方程

本文自研求解器[13-17]基于动态结构化嵌套网格,对雷诺平均NS方程(RANS方程)进行数值求解,可压缩RANS方程如(1)式所示。

(1)

式中:ρ为空气密度;ui是速度分量;p为压强;E为总能;H为总焓。

对于方程中无黏通量采用Roe迎风格式配合WENO插值实现5阶精度,对于方程中的黏性通量采用2阶中心差分格式计算。使用近似因式分解方法进行方程的时间推进,在非定常计算方面,采用隐式双时间步长方法,并在子迭代中使用多重网格和当地时间步长方法加速收敛。

物面采用无滑移边界条件,远场采用基于黎曼不变量的无反射边界条件。

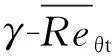
γeff=max(γ,γsep)

(2)

Dγ=ρΩγ(1-Gonset)

(3)

Reθt=F(Iinf)F(λθ)

(4)

1.3 嵌套网格方法

相较于其他方法而言,嵌套网格方法在网格处理方面有2个额外的步骤,即挖洞(hole-cutting)和插值(interpolation)。其中,挖洞是将侵入物面内的网格单元和网格点进行标记,从而在计算中排除这些单元和点。插值是对于嵌套网格块边界处的网格点提供相应的插值模板单元和插值系数,使得流场信息在相互嵌套的网格块之间进行传递。本文挖洞基于Objective X-ray方法,插值采用Inverse Map与模板游走相结合的方法,具体实现方法参考文献[13]。

2 求解器验证

对于文中的转捩模型采用标模平板算例(S & K平板[20]、T3A平板[21-22])和S809翼型[23]进行验证,对计算得到的表面摩阻因数、压力系数等结果与相应的试验结果进行比对,说明求解器转捩模拟的能力。

3个算例的来流湍流度及所采用的计算网格规模在表1中列出,其中J为流向,K为物面法向。S809翼型计算网格在图1中给出。

表1 验证算例计算状态和网格规模

对平板标模算例,对比了CFD计算与试验测得的表面摩阻因数,而对S809翼型算例,对比了翼型表面压力系数。对比结果如图2～3所示,3个验证算例的计算结果展示出了求解器在转捩模拟方面良好的预测能力和精度。

由3个作用点处的截面直径，换算出该截面处的惯性矩I的均值分别为：1.91e4，8.94e3，5.14e3mm4。弹性模量均值为24.41MPa，带入式(7)分别得到以下3个关系式，即

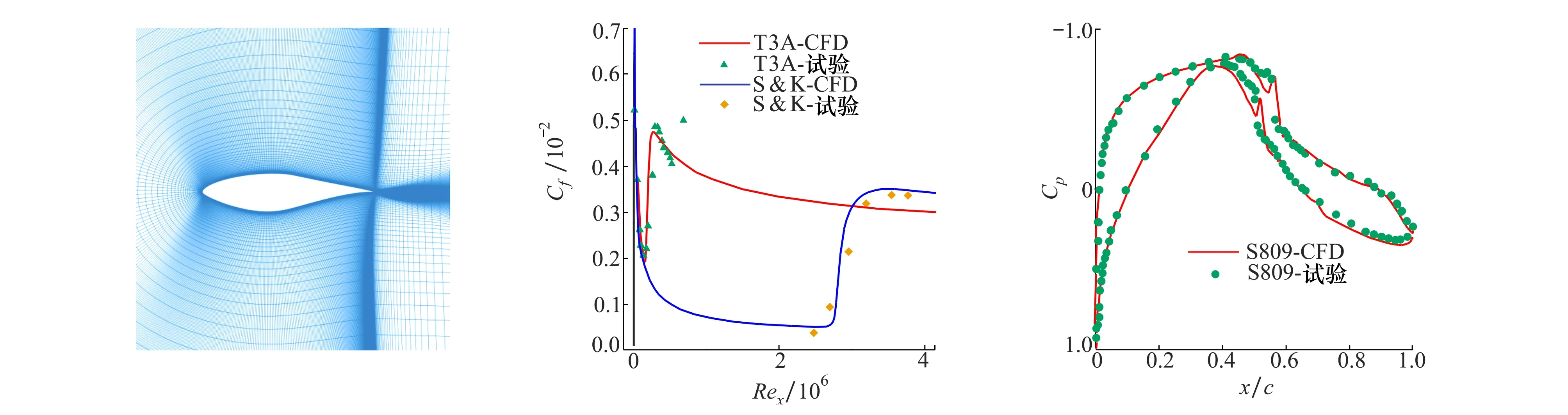
图1 S809翼型网格 图2 平板标模算例表面图3 S809翼型表面压力系数对比结果 摩阻因数对比结果

3 计算模型与网格

3.1 计算模型

计算模型采用HPW工作会议提供的旋翼标模算例-PSP旋翼,其桨叶平面及截面翼型形状如图4所示。此旋翼共包含4片桨叶,半径为1.689 m,参考弦长为0.138 m,桨叶实度σ为0.103 3,在0.95R处有30°的后掠角,桨叶转速为1 150 r/min,对应的桨尖马赫数为0.58,基于桨叶平均弦长和桨尖速度的雷诺数为1.87×106。

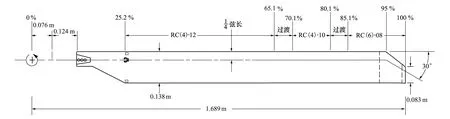
图4 PSP旋翼桨叶平面形状

该旋翼的风洞试验于2016年在NASA-LaRC旋翼测试中心[24]完成,由于试验论文中并未提及相应的风洞试验湍流度,在本文转捩计算中,湍流度设为0.7%。

3.2 计算网格

HPW工作组公开发布了PSP旋翼标模桨叶的几何文件和表面网格文件,本文利用上述表面网格文件生成了相应计算网格,包含对应于4片桨叶的贴体网格和笛卡尔背景网格。背景网格在桨叶附近进行加密处理。总网格点数为5.1×107,其中贴体网格点数为4.4×107。贴体网格中桨叶表面法向首层网格距离为8.9×10-7m。背景网格最密的网格尺度为1/10倍的桨叶弦长。远场网格距离旋转中心约为20倍的桨叶半径长度。图5给出了桨叶贴体网格的3个截面和最密背景网格的1个截面,以及相应的挖洞结果。

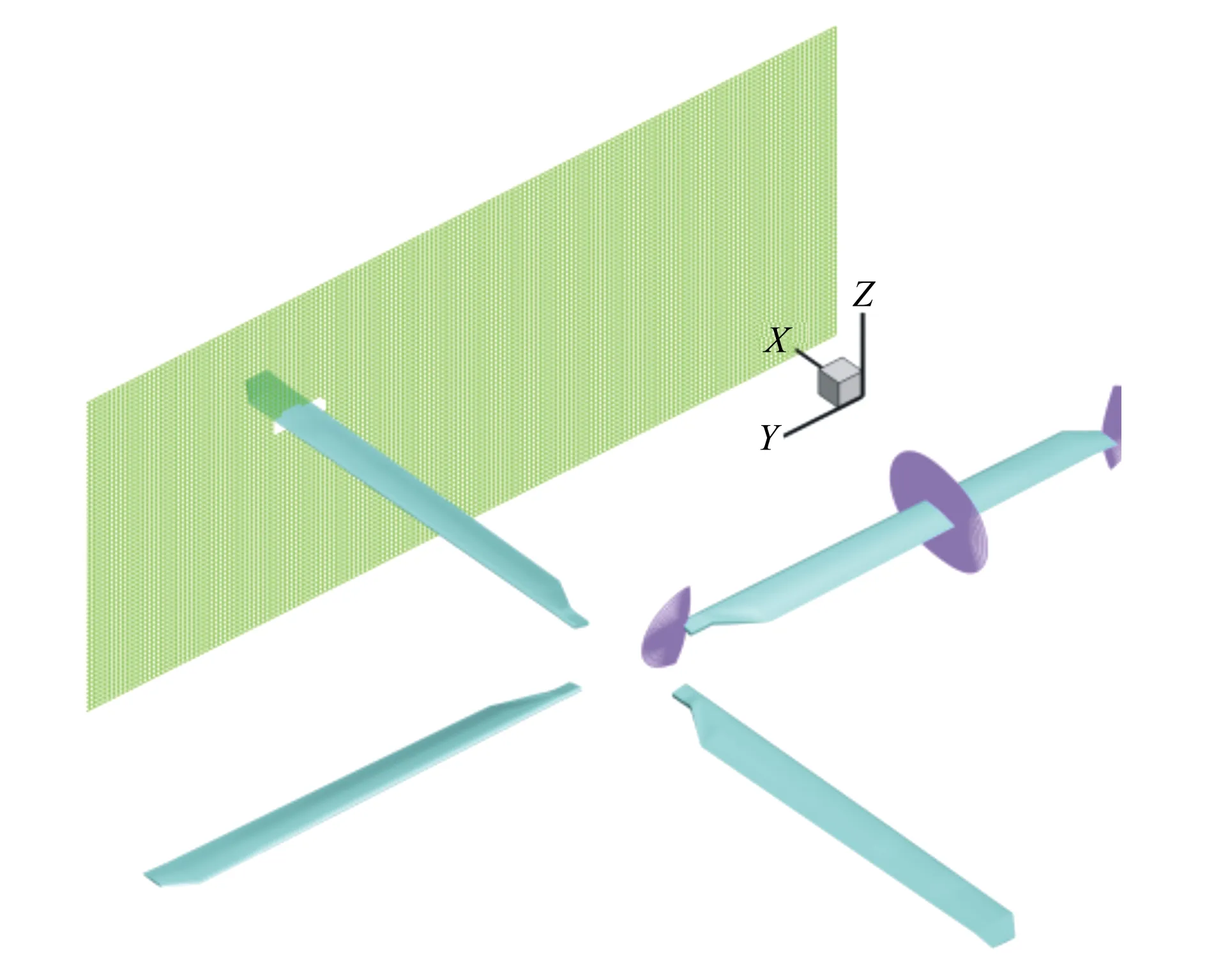
图5 PSP旋翼标模嵌套网格

4 计算结果与讨论

4.1 旋翼积分力

在悬停状态下,旋翼有2个最重要的气动力系数,即拉力系数CT和扭矩系数CQ。按照HPW工作组的统一定义,(5)式给出了这2个系数的计算公式。

(5)

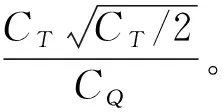
在本文计算中,重点对比同拉力系数下的扭矩系数和相应的悬停效率。所有的计算结果均为旋翼最后一个旋转周期内的平均值。表2和图6给出了悬停效率的计算结果与试验结果的对比,图中试验值的误差限取自文献[24]中给出的最小值。该结果验证了本文所采用的求解器对于旋翼悬停气动力系数计算的可靠性,转捩模拟结果和全湍模拟结果计算误差均在5%之内。

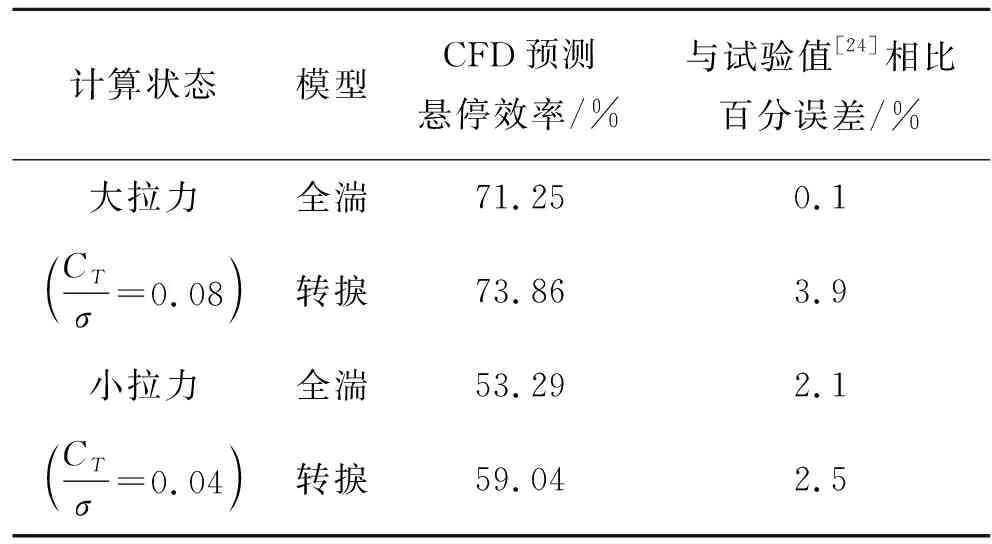
表2 CFD预测悬停效率及误差

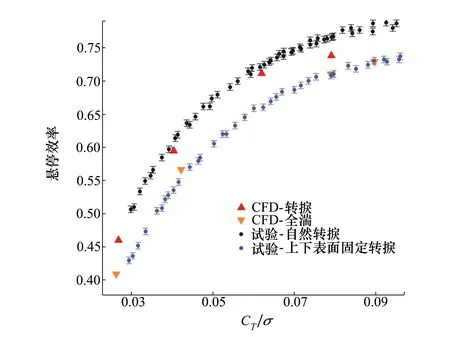
图6 CFD预测旋翼气动性能与试验值对比

对于悬停效率这一评价旋翼气动效率的重要参数而言,在低拉力状态下,转捩模拟得到明显优于全湍模拟的结果(约高10%),但是在大拉力状态下,这一优势逐渐缩小(约高4%)。

4.2 截面压力分布及桨叶载荷分布

(6)

式中:Ω为转速；r为当地半径；c为当地弦长。

4.2.1 截面压力分布

沿桨叶展向从30%R处开始至80%R处结束,截取了6组压力分布,对比结果如图7～8所示。其中图7为小拉力状态下结果,图8为大拉力状态下结果。

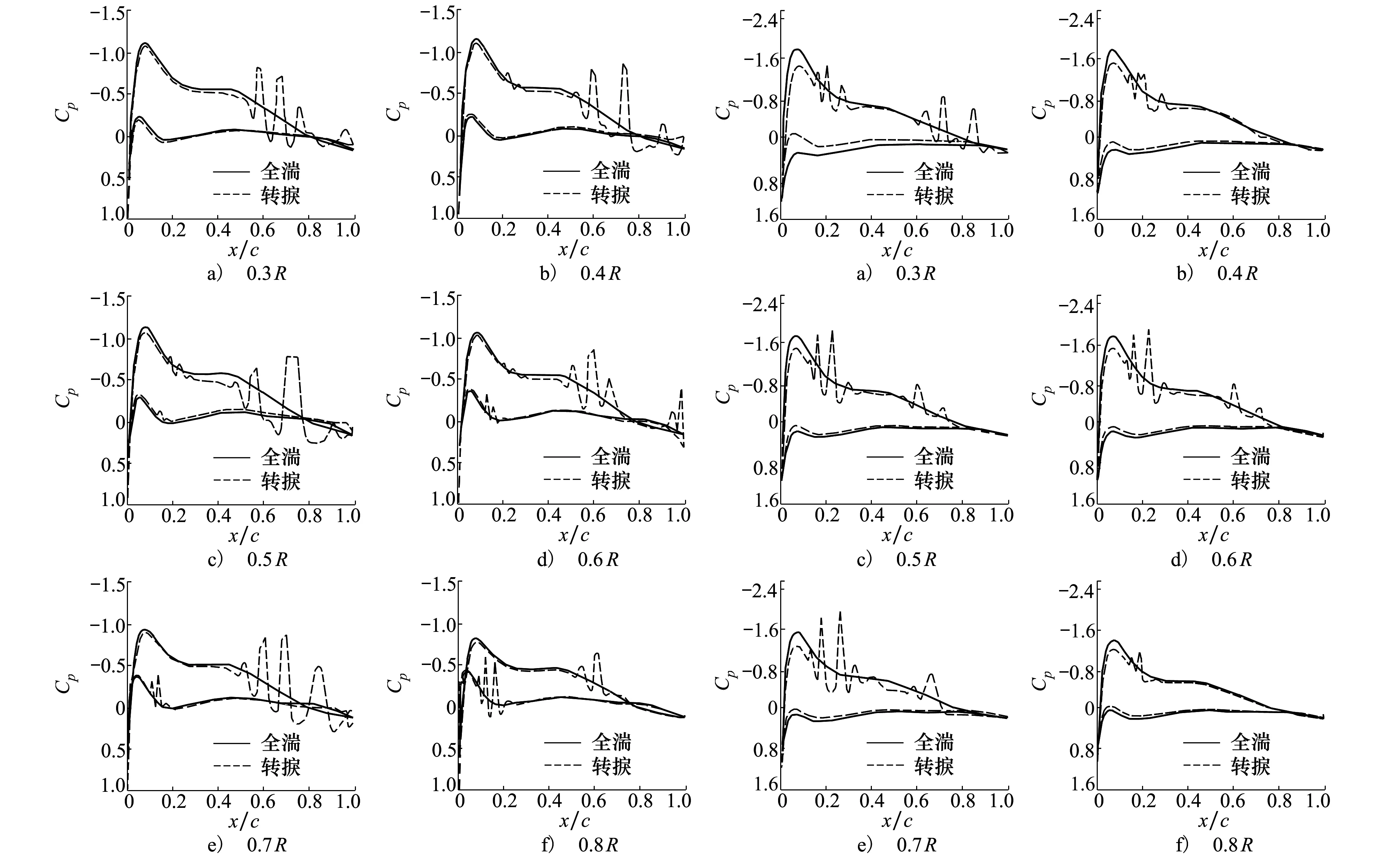
图7 小拉力状态桨叶截面压力分布对比 图8 大拉力状态桨叶截面压力分布对比

相比而言,全湍流模拟结果得到了比较平滑的桨叶表面压力分布,而由于计入了流动转捩过程,转捩模拟得到的表面压力分布在流动转捩区域附近出现了明显波动。在其余区域,两者压力分布相似且重合度高。

通过桨叶截面上下表面压力的波动可以判断出桨叶转捩发生的区域,经过对比与试验[24]中给出转捩位置保持一致。进一步证明了本文所采用的求解器在旋翼悬停自然转捩模拟上的可靠性。在小拉力状态下桨叶表面出现较大范围的层流流动,而随着旋翼拉力的增大,该层流范围逐步减小,这与4.1节中旋翼积分扭矩系数变化趋势保持一致。

4.2.2 桨叶载荷分布

图9给出了不同拉力状态下,全湍流以及转捩模型计算得到的桨叶载荷系数在桨叶展向上的分布,其中拉力系数分布呈现出合理的类椭圆形分布。

图9 桨叶载荷分布对比

虽然截面压力分布在转捩区域有明显的波动,但是对于沿桨叶展向的拉力系数,除了桨叶根部小拉力区域,2种模拟方法并没有表现出很大的不同。而对于沿桨叶展向扭矩系数来说,由于转捩模拟中部分区域存在明显的层流流动,在这部分区域转捩模型预测得到的扭矩系数要低于全湍模型预测的值。在大拉力状态下,由于表面层流范围的缩小,全湍模拟和转捩模拟得到的扭矩系数分布也趋于一致。

4.3 桨叶表面流线及旋翼尾迹流场形态

4.3.1 桨叶表面流线

图10～11分别显示出不同拉力状态下桨叶上、下表面的表面流线,可看出全湍状态下桨叶表面流场变化平缓,但是转捩模拟得到了明显不同的桨叶表面流线,其表面流线变化明显,在桨叶内侧上表面发生了明显的流动分离现象,这一现象在全湍模拟中并没有出现。表面流线的明显差异也进一步说明了4.2.1节中2种不同模拟方法得到的差异明显的桨叶截面压力分布。

图10 小拉力状态桨叶表面流线对比

图11 大拉力状态桨叶表面流线对比

4.3.2 尾迹流场

通过Q判据等值面,图12给出了不同拉力状态下旋翼桨盘下方的尾迹桨尖涡分布,利用涡量大小在对应的Q等值面上进行相应的染色。根据上述计算结果,转捩过程引发的桨叶表面分离对桨尖涡的影响较小,但是对于桨盘下方小于桨盘半径处的尾迹结构有比较明显的影响。同时,随着拉力的增大,桨尖涡的结构形式出现了一些变化,尾迹流场中开始出现围绕着桨尖涡的二次涡结构,这一现象在全湍和转捩模拟中均有所表现。

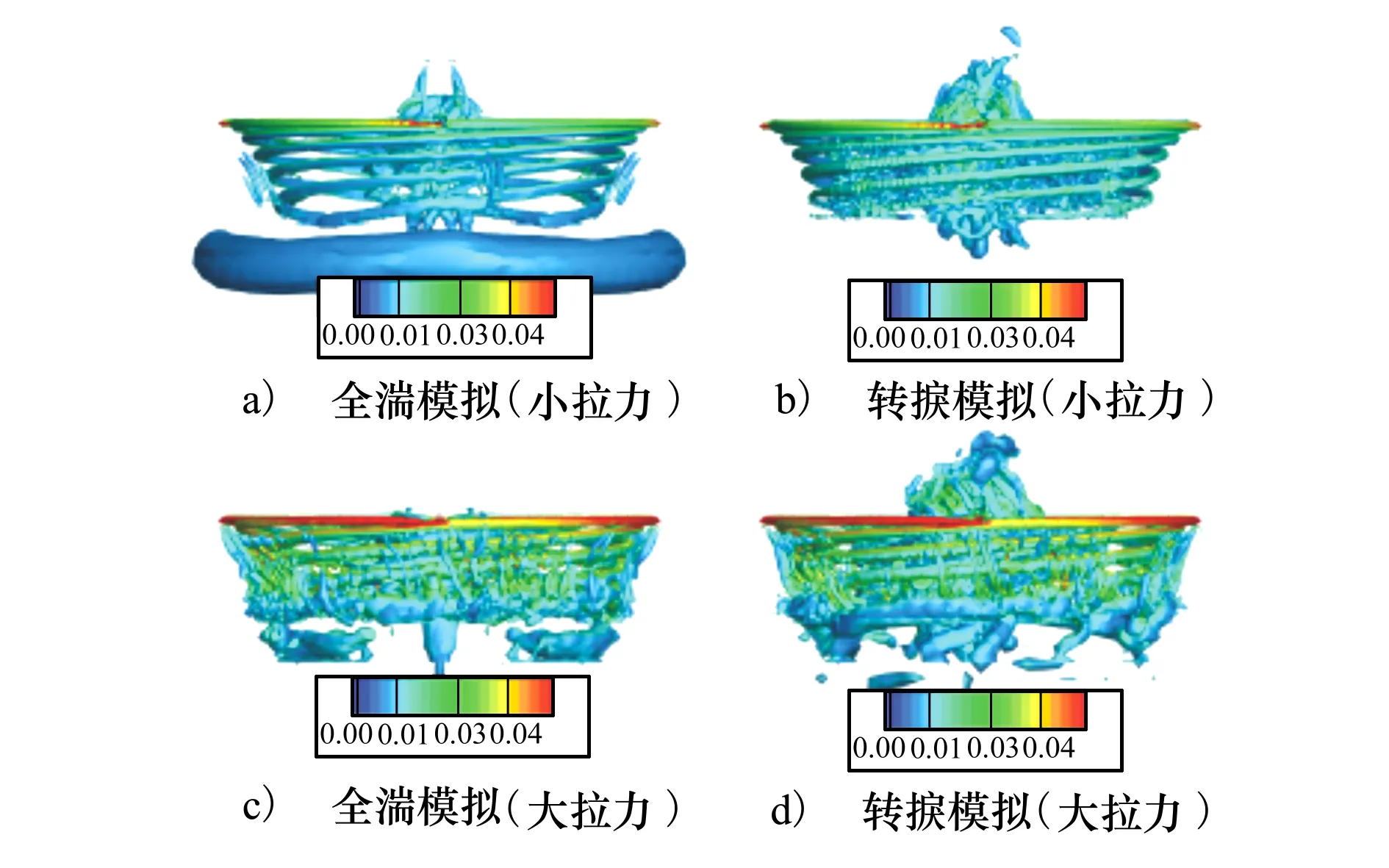
图12 旋翼尾迹流场对比

5 结 论

本文利用自研RANS求解器,对AIAA HPW工作组提供的PSP旋翼标模,在悬停状态下,分别进行了全湍流模拟和转捩模拟。

计算结果首先表明本文CFD模拟得到的旋翼拉力-悬停效率曲线与试验重合度高,计算误差在5%之内,并且转捩模拟中,CFD方法能正确模拟出桨叶表面流动的转捩位置。由此,证明了本文求解器在旋翼悬停流场模拟方面的可靠性。

其次,通过全湍与转捩模拟结果的对比发现,转捩过程对桨叶截面压力分布、沿桨叶展向扭矩分布以及桨叶表面流线均有显著影响,而对沿桨叶展向拉力分布影响较弱。转捩过程给桨叶截面压力分布带来了明显的波动以及桨叶表面流场的明显分离。相比于全湍结果,转捩模拟在层流区域得到了更低的扭矩系数,从而带来了悬停效率4%～10%的增量。

最后,对于旋翼桨盘下方桨尖涡,转捩过程没有明显影响,但是由于转捩过程带来的流动分离,对于内侧桨叶下方尾迹区域,转捩过程带来了明显的影响。