复杂纹理瓷砖表面缺陷检测算法研究

欧阳周, 张怀亮, 唐子暘, 彭玲, 俞胜

(1.中南大学 高性能复杂制造国家重点实验室, 湖南 长沙 410083; 2.中南大学 机电工程学院, 湖南 长沙 410083)

近年来，中国陶瓷砖产业转型升级和发展取得巨大的成果，截至2019年，我国形成比较大的陶瓷砖产业集群22个，全国陶瓷砖企业1 500多家，年产量82.2亿平方米，全年市场营收收入超3 877亿元(中瓷网数据)。但我国瓷砖依旧未摆脱瓷砖品质普遍偏低的困境，处于“大”而不“精”的现状。瓷砖生产领域的产品缺陷检测手段主要依赖于人工检测，在检测速度和检测准确率上因个体之间能力差异存在很大的不确定性。

在瓷砖视觉检测领域，意大利System公司[1]应用线阵相机结合PSD的方法实现了瓷砖平整度的检测；美国某检测公司[2]设计的检测分类系统实现了瓷砖色差、尺寸、平整度方面的检测；Hanzaei等[3]通过缺陷区域的几何特征分析，实现了对缺陷瓷砖的检测分类；国内的邹庆胜等[4]实现了单色瓷砖的色差、直角度、尺寸、针孔的多参数检测。但以上所提及的系统、方法的应用场景受限于瓷砖的色差、尺寸、平整度等参数的检测或是单色简单纹理瓷砖的缺陷检测。权小霞等[5]通过含缺陷瓷砖图与标准瓷砖图对比，提出了一种基于局部方差加权信息熵的检测算法，实现了缺陷检测；Treisman等[6]提出的特征融合理论使视觉显著性计算成为可能；Itti等[7]利用颜色、对比度、方向3个特征建立了最早的显著性检测模型；此后，Perazzi等[8]通过局部和全局特征的度量获得显著图，利用高维高斯滤波器依次对各个像素赋予相应的显著值；Casagrande等[9]提出了一种结合图像处理方法的瓷砖缺陷自动检测方法，发现将SFTA与DWT结合使用可显著提高总体精度。Mishra等[10]提出了一种基于人工神经网络(ANN)的技术，该技术利用瓷砖图像的变换域特性，通过系统学习模型的能力使其具有灵活性和动态可配置性。仿真结果也验证了该算法的优势之处。Zhang、孙丰东、Cheng等[11-13]都分别提出了多种不同的显著性检测模型。

为解决现有瓷砖缺陷检测方法准确率低和稳定性差等问题，本文引入基于视觉注意机制的显著性目标检测方法，并将其运用到瓷砖表面缺陷检测的研究，开展针对纹理瓷砖表面缺陷检测的研究，实现抗瓷砖表面纹理干扰检测，这对于瓷砖的自动化检测发展具有重要意义，也是实现复杂纹理瓷砖在线检测的关键一步。

1 图像的采集与预处理

根据瓷砖缺陷区域的成像特征,采用改进传统单尺度SSR光照校正算法和双边滤波处理进行预处理。传统的单尺度光照校正存在一定的局限性，因此图像预处理中必须先对其校正方式进行相应改进，以适应实际的检测需求。根据瓷砖缺陷区域的成像特征，改进传统单尺度SSR光照校正算法的下限取值方式，具体步骤如下：

1) 选取多幅表面存在缺陷的瓷砖图像作为数据样本，定位并提取相应的缺陷区域；

2) 提取各个缺陷区域对应的三通道数值，并计算其均值， 依据三通道数据与数值均值的分布关系，求取相应的权重；

3) 分别求取各通道的加权均值作为该通道的数值波动下限参数，替代原算法中寻找最小值操作；

4) 统计图像中有任一通道值小于对应通道下限的像素，记为待定像素(原图像与待定像素对应点不进行光照校正计算)；

5) 依据待定像素的坐标，对应生成二值图，其中与待定像素对应点置1，其余置0，作为后续疑似区域补充信息。

对于像素点通道值小于设定值的点，直接定义为疑似缺陷区域的像素点，采用步骤4)～5)进行处理。

双边滤波作为一种基于加权平均的非线性滤波器，既考量了像素的欧式距离，又考量了像素区域的辐射差异，可以有效地实现边缘保持、平滑去噪。经双边滤波后的图像和权重系数w(i,j,k,l)表达式为

改进方法与SSR算法结果对比如图1～2所示。

图1 SSR光照校正后图像结果

图2 改进单尺度算法以及双边滤波处理后图像结果

对比图1和图2，依次经过光照校正和双边滤波处理后的图像实现了保持边缘、降噪平滑的目的，同时使得图像具有更好的区域块聚集性，方便图像各类颜色像素统计，有利于后续缺陷检测的实现。

2 基于视觉注意机制的瓷砖缺陷检测

2.1 颜色空间的处理和瓷砖表面特征提取

视觉注意机制直接决定了检测模型对外部信息的辨别处理能力，关系复杂纹理瓷砖表面缺陷的显著性检测到最后模型检测结果的正确与否[14]。因此本文的研究主要采用基于数据驱动的自底向上的视觉注意机制显著性检测方法，如图3所示。

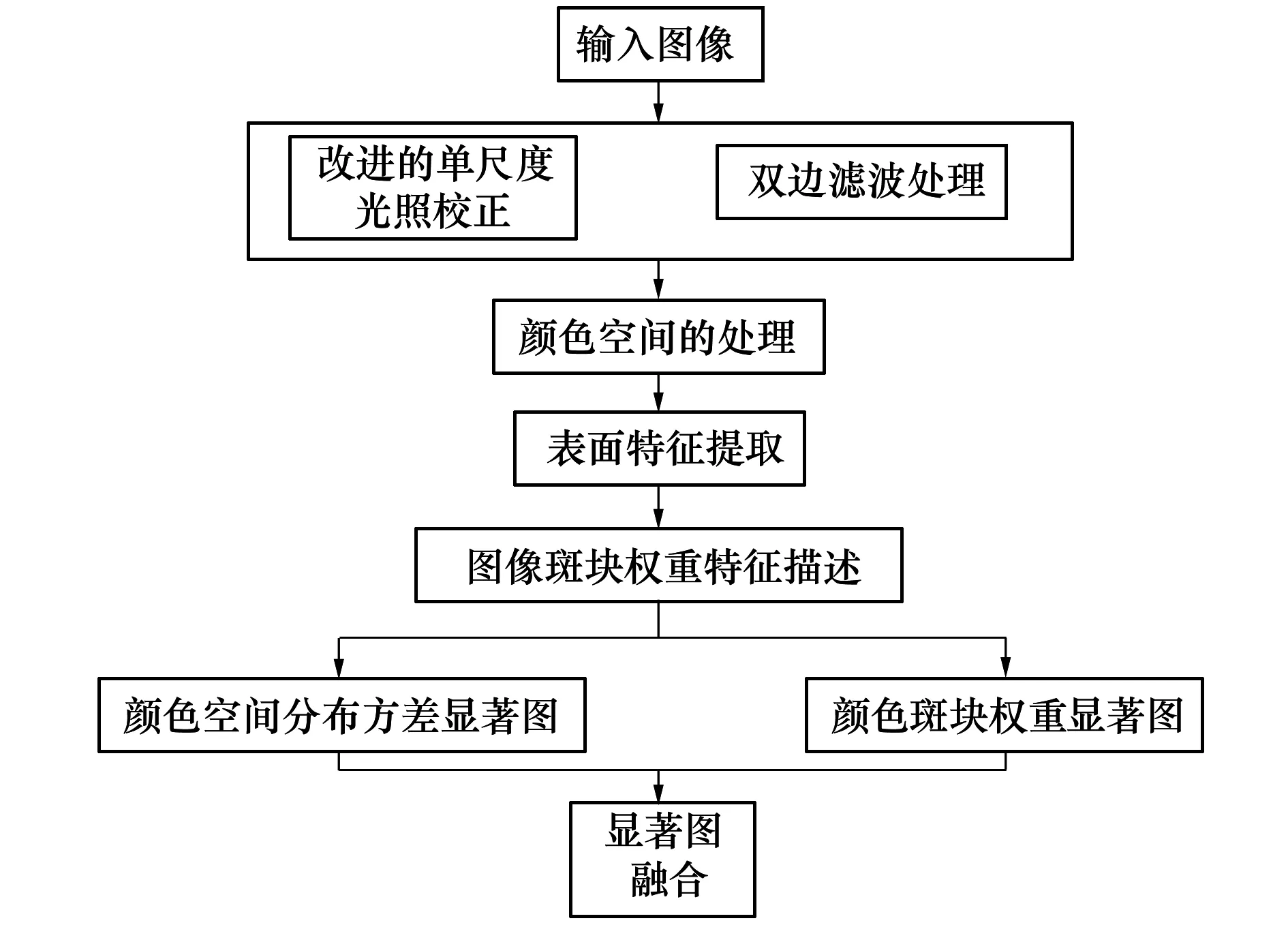
图3 基于视觉注意机制的瓷砖缺陷检测模型框图

颜色空间处理能将HSV(色调、饱和度和明度值)空间模型的三通道都压缩至5个量级，共描述125种颜色，在实际检测中单图像颜色种类可控制在50种以内。经过颜色空间处理之后，可得到图4所示的表面斑块破损的瓷砖图像。

图4 表面斑块破损瓷砖图像

根据视觉注意机制中对比性原理及高频抑制原理，结合“成像性”与“聚集性”，即瓷砖的表面缺陷成像颜色相对一致，空间分布相对聚集，且瓷砖的背景纹理成像颜色相对一致但空间分布相对分散。可以通过改进图像方差特征公式, 从求取图像灰度的不均匀性转而求取各类颜色像素的空间分布方差，其计算表达式为：

对图像的各类颜色进行统计，并依据各类颜色像素的频数进行降序排列，然后对各类颜色逐一进行颜色空间分布方差计算。选取具有代表性的9种颜色对应的分布方差计算值，分别为319.64,333.08,267.67,399.98,303.56,208.49,9.75,2.65和2.23，如图5所示。将图5a)～5g)所代表的颜色分布方差进行对比，图5a)～5g)所代表的颜色RGB值为(180,217,211),(152,152,83)和(99,105,87)，如图6所示。

图5 各类颜色的分布方差值

从图5a)～5e)可以看出，瓷砖修饰纹理分布较为分散，其分布方差值也较大，而图5g)为缺陷区域图像，分布较为集中，其分布方差值较小。从图5a)～5b)、5g)和图6可以看出，图5g)中的方差值明显低于其他纹理特征。而图5h)和5i)是颜色统计过程中的一些小类颜色杂质像素，后续需要对其进行有效剔除处理。依据公式计算出各类颜色的空间分布方差后，即可分配各类颜色对应的显著值，显著值的分配准则为：方差越小，显著值越大。

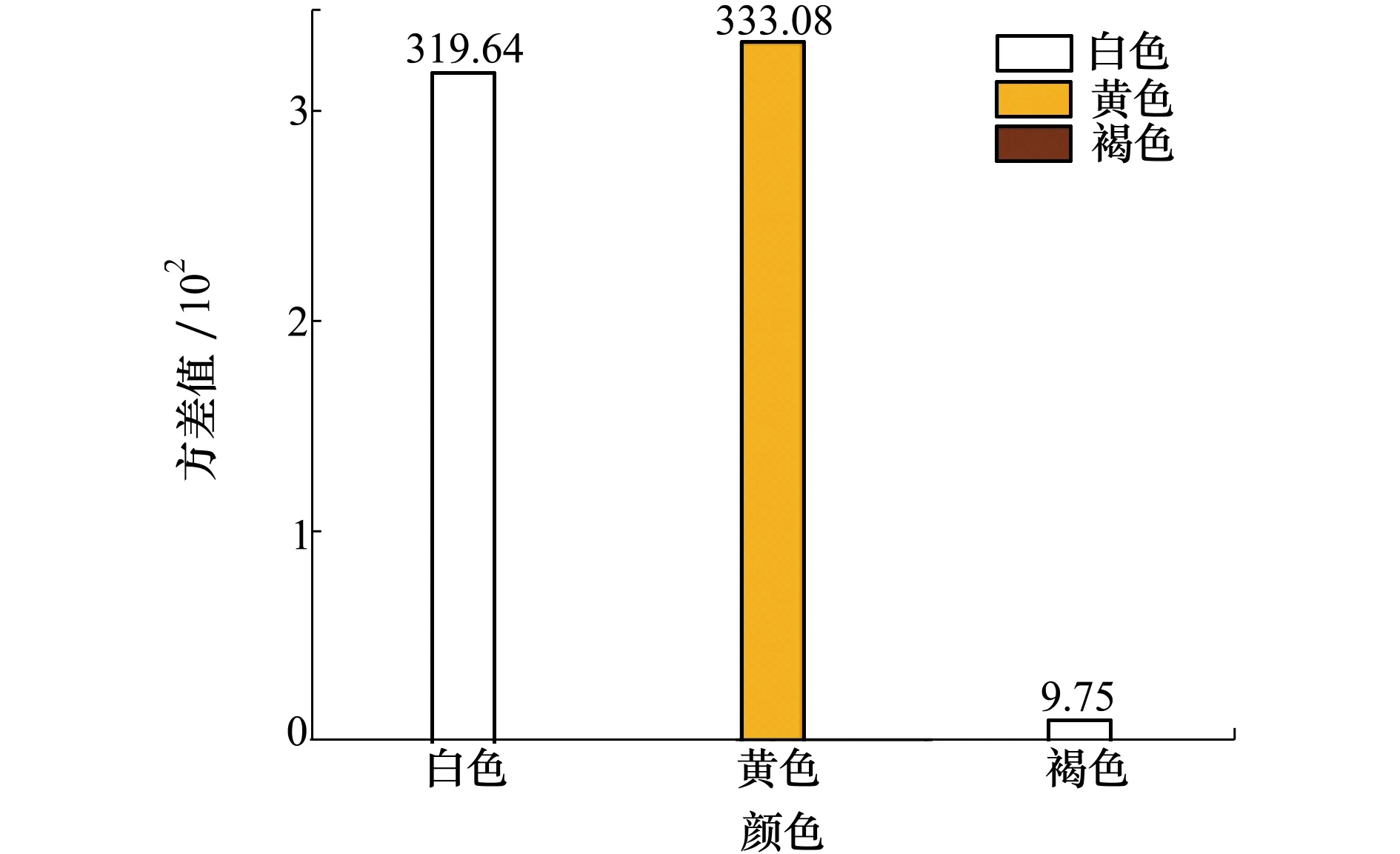
图6 3类颜色的分布方差值

依据显著性原理分配各类颜色的显著值后，对像素逐一进行显著性赋值，即可获得颜色空间分布方差显著图，如图7所示(瓷砖缺陷在图中用红色矩形标记)。

图7 各类颜色的空间分布方差显著性

从图7可以看出，颜色空间分布方差特征有效地实现了对瓷砖表面缺陷区域的检测，克服了表面纹理为背景信息的干扰。但是仍然存在着一些颜色种类的干扰，甚至其显著性值处于高位状态，需要进行进一步的图像处理。

2.2 图像斑块权重特征

在瓷砖表面特征提取之后，仍有可能出现图8所示的情况(瓷砖缺陷在图8a)中用矩形标记)。

其中图8b)中绿圈表示的是真实缺陷区域和非缺陷的干扰像素, 这两者会出现在同一种颜色分量分布图中的原因是瓷砖背景纹理有小块纹理颜色与缺陷区域颜色接近，二者在光照校正处理和颜色种类降级处理之后被划分成了同一颜色。为了进行缺陷区域的有效区分判断，在此引入斑块权重来描述不同级别的特征，斑块权重Uij表达式为

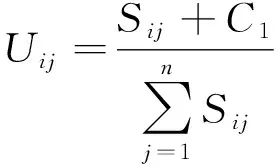
(5)

式中：Uij为第i种颜色的显著值；C1为增益因数；Sij代表的是第i种颜色第j块独立子区域的面积。

图8 缺陷检测对照

依据公式计算出各类颜色的斑块权重后，即可分配其对应的显著值。以图4为例，对各类颜色依据显著性准则计算其子区域的显著值，获得的各颜色斑块权重显著图，与图5对应的9种颜色对应的分布方差计算值图，如图9所示。

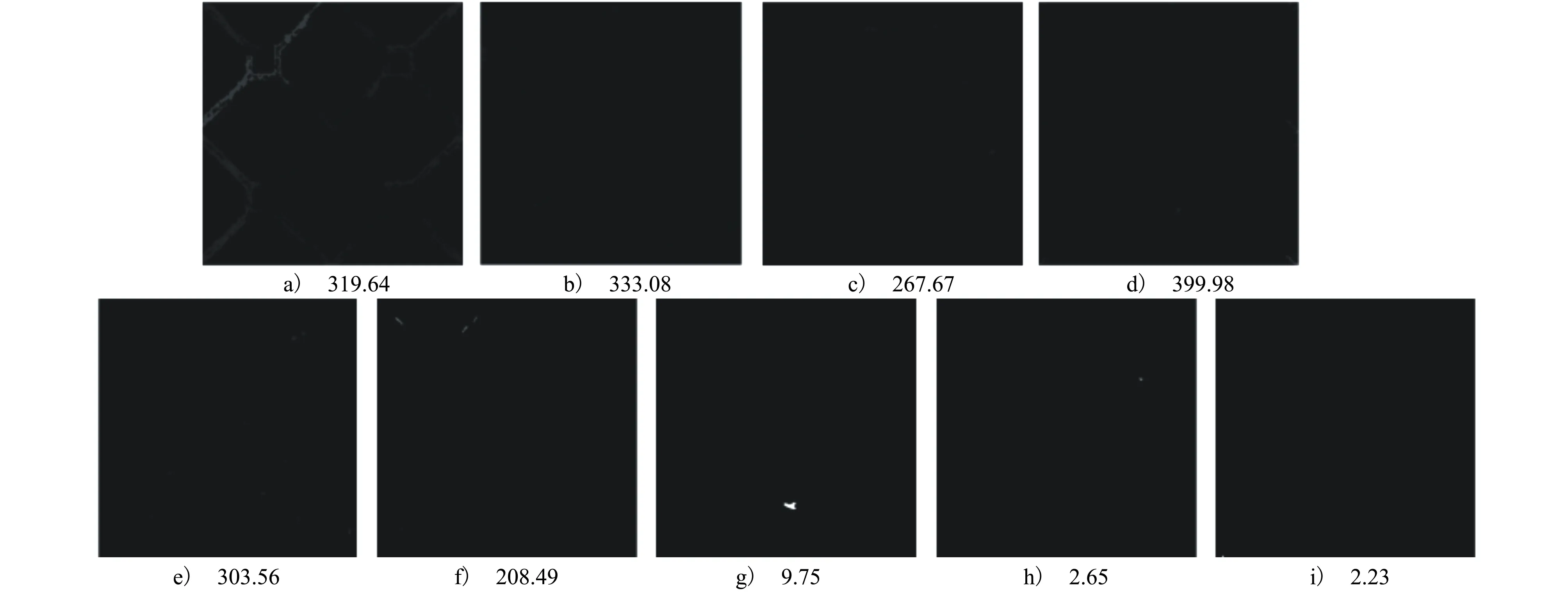
图9 各类颜色的斑块权重

图9先将图像的各类颜色进行统计，再依据各类颜色像素的频数进行降序排列成图9a)～9i)。由图可知：对于像素数量大、分布广泛的颜色种类，例如图9b)～9e)，其斑块权重的显著值均较小，使得整个显著图呈现“黑色”；图9a)和图9f)虽然仍存在一些纹理斑块，但其显著值处于低位状态，大比例的纹理像素的显著值都得到很好抑制；图9g)作为缺陷区域，保持了较好的高亮性，其显著值处于高位状态，符合检测的要求，而图9h)和图9i)作为小数量像素的干扰现象仍存在，需要进行图像的后处理进行剔除。通过对各类颜色的斑块权重图进行叠加，得到图像颜色斑块权重显著图如图10a)所示(瓷砖缺陷在图中用红色矩形标记)。对比图10a)和图9的9个图可以看出，颜色斑块权重特征也可以有效地实现对瓷砖表面缺陷区域的检测，可以有效克服纹理背景的干扰。

图10 瓷砖图像显著图

2.3 显著图融合

经过图像特征描述分析后，分别获得了颜色空间分布方差显著图和颜色斑块权重显著图。为了获得一张最具代表的显著图用以缺陷检测判别，采用指数函数形式，融合2个描述特征，最终融合的显著图SQ(x,y)具体表达式如(6)式所示。

SQ(x,y)=C2·Q(x,y)exp(B(x,y))

(6)

式中：C2为增益系数；B(x,y)是叠加后的各类颜色的斑块权重图。

依据表达式计算，有效地融合了颜色空间分布方差显著图和颜色斑块权重显著图，获得了新的瓷砖检测显著图，具体融合后的显著图如图10b)所示(瓷砖缺陷在图中用红色矩形标记)。从图10b)可以看出，相较于单独特征的显著图，融合后的显著图有效地保留了真实的缺陷区域，而其余纹理背景区域得到了更好的淡化抑制，使其显著值处于低位状态，使得检测更为准确。依据最大类间方差法对特征融合显著图进行二值化的阈值求解，并将其转化为二值图，如图10c)所示(瓷砖缺陷在图中用红色矩形标记)。

2.4 缺陷判定

在图像斑块权重显著图中，仍然存在一些由于小类颜色种类以及像素颜色压缩降级导致的一些不同颜色像素的错误合并，会出现一些“小而强”像素点。因此在获得融合的显著图后，需要对其进行剔除。这些奇异点往往所占像素数量较小，连通性差，因此根据连通性特点对其进行剔除。

本文采用八邻域模型，实现对二值显著图中连通域的寻找和标记，二值显著图经过连通域寻找和标记后，即实现了对图像中子块区域的划分和标序，即可按其标号依次进行各子块区域面积的计算，而面积的计算实质上就是具有相同标号子块区域的像素数目统计。通过分析子块区域大小实现取舍：若子块区域小于设定阈值，则像素值置0，剔除；反之，则置1，保留。经奇异点剔除操作后，获得的最终显著图如图11a)所示(瓷砖缺陷在图中用红色矩形标记)。采用最小外接矩形方法进行缺陷标记，如图11b)所示。(瓷砖缺陷在图中用红色矩形标记)。由图11可知，判定之后得到瓷砖缺陷图像与实际情况吻合。

图11 瓷砖缺陷检测结果

3 实验结果及分析

3.1 图像数据

为了验证本文提出的算法有效性，将本文的SOD算法与文献[9]中研究的基于分割的分形纹理分析算法(SFTA)和文献[10]中研究的人工神经网络算法(ANN)进行对比，将3种不同的瓷砖检测算法应用于图12所示的3种不同的复杂纹理瓷砖缺陷检测。实验采用3类不同纹理的瓷砖进行测试，每一类瓷砖有合格瓷砖64块与不合格瓷砖30块，瓷砖纹理如图12所示。

图12 实验瓷砖

3.2 评价指标

采用定量评估进行实验结果分析，涉及以下参数：

TP：瓷砖无缺陷，判为无缺陷；

FP：瓷砖有缺陷，判为无缺陷；

FN：瓷砖无缺陷，判为有缺陷；

TN：瓷砖有缺陷，判为有缺陷；

准确率(Accuracy)、精确率(Precision)、召回率(Recall)和综合率(F-Measure)的公式分别为：

3.3 实验结果与分析

依次对3类瓷砖的样本图像进行缺陷检测实验，检测结果的准确率、精确率如表1所示。取其中的综合检测率为对比对象，比较3种算法[9-10]的优劣如图13所示。

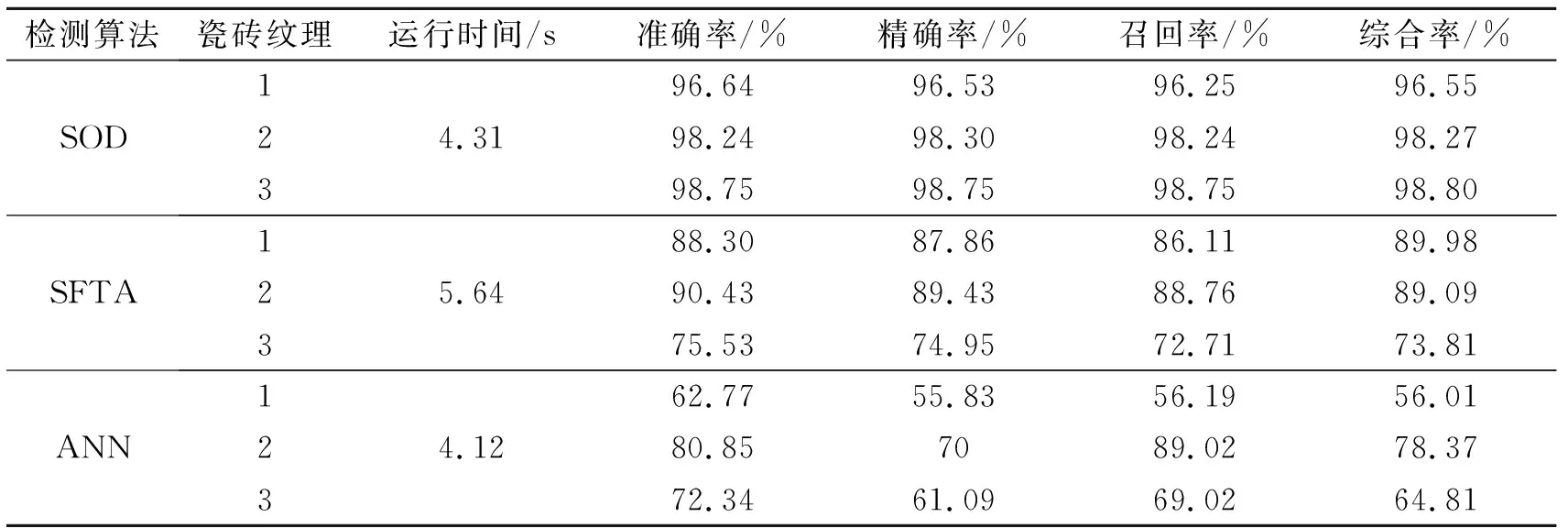
表1 指标结果

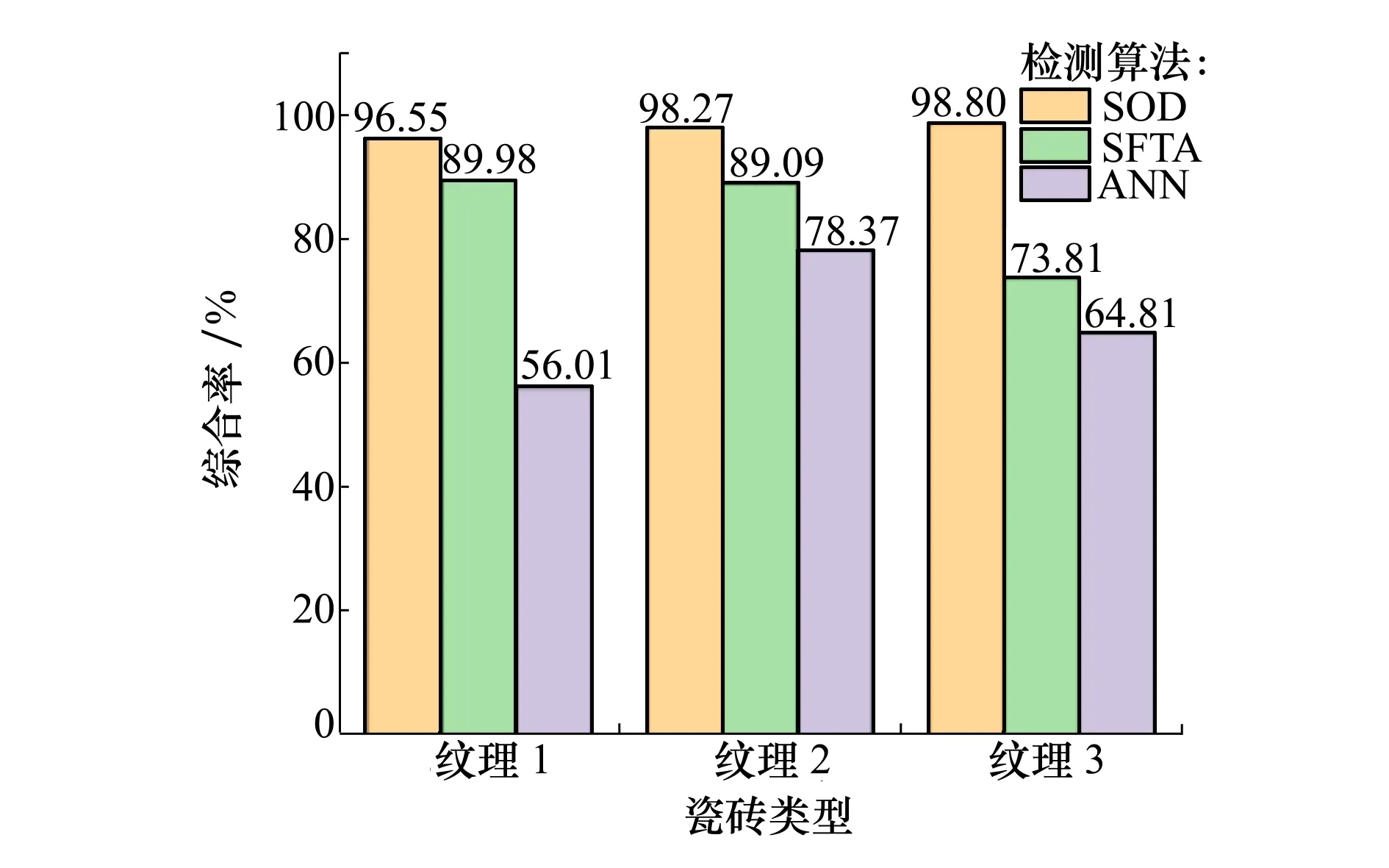
图13 评价结果

从上述结果可以看出，基于视觉注意机制的复杂纹理瓷砖表面缺陷检测算法，针对随机选取的3类复杂纹理瓷砖均具有良好的检测效果，检测效果评价指标均达到90%。本文提出的针对复杂纹理瓷砖表面缺陷检测的SOD算法，在3类复杂纹理瓷砖的检测效果良好，4项评价指标也均处于较高水平。分析各评价指标，其中综合率作为最重要指标，SOD算法模型的检测准确率均达到了96%以上，说明了SOD算法模型的稳定检测性能。相比较于其他算法，本文研究的SOD缺陷检测算法更适合于复杂纹理瓷砖表面的缺陷检测，也从侧面说明了SOD算法模型具有较低的误检、漏检率。而ANN算法适用于市面上大多数普通瓷砖的缺陷检测，对于本文研究的复杂纹理瓷砖检测效果在算法复杂度上有优势，但检测率欠佳。综上所述，本文提出的瓷砖缺陷检测算法有较好的检测性能，符合实际检测需求，具有一定的实际意义。

但检测结果仍存在一定的误差，主要由于一些小类颜色种类以及像素颜色压缩降级导致颜色接近像素的错误合并，形成一些具有大连通域的奇异点，超过了利用连通域筛选的阈值，造成误检。

4 结 论

1) 改进了单通道SSR光照校正算法的数值下限选取方式，图像实现了保持边缘、降噪平滑的目的，方便图像各类颜色像素统计，有利于后续的缺陷检测实现。

2) 提出了一种新的复杂纹理瓷砖表面缺陷检测算法，建立了基于视觉注意机制的瓷砖缺陷检测模型。通过压缩HSV颜色空间各通道的数量等级，实现像素颜色种类数目的降低，提高了瓷砖表面缺陷检测精确性和稳定性并降低了运算处理量。

3) 随机选取3类复杂纹理瓷砖进行实验，对比3种不同的检测算法。实验结果表明，本文提出的缺陷检测算法针对3类实验复杂纹理瓷砖均达到了96%以上的综合检测率，比SFTA缺陷检测算法和ANN缺陷检测算法拥有更高的检测率。证明了本文提出的针对复杂纹理瓷砖表面缺陷显著性检测模型的正确性以及检测算法的稳定性。