执行器跳变故障的失效卫星轨迹跟踪控制
路阳, 蔡彬, 乔道鹏, 付艳明, 张卯瑞
1.哈尔滨工业大学 控制理论与制导技术研究中心, 黑龙江 哈尔滨 150001;2.北京电子工程总体研究所, 北京 100854
在轨卫星在运行时,系统元部件不可避免地会出现故障情况,从而导致卫星失效。将在轨失效的卫星捕获后进行修复或者燃料加注等操作,可以提升其工作效率,这对卫星产业的可持续发展具有重要意义[1-2]。与失效卫星进行交会对接是实现上述在轨操作的关键性技术,对该问题的研究已经成为一个热点。目前,国内外学者对这一问题展开了一系列研究。文献[3]利用参量Lyapunov方程,设计了交会过程中执行器受限情况下的控制器,其目的是改变系统的增益以改善系统的动态性能。文献[4]针对卫星近距离段交会对接过程中的姿轨耦合控制问题,利用滑模自适应控制方法设计了一类六自由度姿轨一体化控制器。文献[5]考虑卫星在拦截任务过程中,系统所面临的参数不确定性和干扰情形,设计了使系统鲁棒稳定的控制器。文献[6]研究了防止碰撞约束下最小能量的连续推力交会对接。文献[7]研究了近地轨道电磁卫星编队飞行中的控制问题,提出了一种自适应控制律使得编队可以保持和重构。文献[8]考虑卫星沿椭圆轨道运行时的近距离交会轨迹安全问题。
当在轨运行卫星的执行部件发生故障时,可能会使得系统失稳,从而增加控制难度。本文以文献[9]中卫星轨迹跟踪控制的参数化方法为基础,提出了跳变控制输入的方法来解决这一问题。该方法基于Markov跳变系统,利用Markov跳变性质的输入,对执行器发生故障的卫星进行轨道控制。有关Markov跳变系统方面的研究,文献[10]研究了Takagi-Sugeno(T-S)模糊型跳变系统的保性能控制问题。文献[11]研究了带有乘性噪声和具有Markov跳变参数的随机离散周期系统的鲁棒控制问题。文献[12]研究了跳变系统的二次型稳定性问题,并且给出了其在RLC电子电路中的应用。文献[13]对含有有限能量干扰的Markov跳变系统进行了研究,给出了此类跳变系统的模型跟踪控制问题的一种有效解法。文献[14]研究了系统含随机扰动以及转移概率未知但是有界情况下离散跳变系统的H∞控制问题,以LMI的形式求解了状态反馈控制器。
Markov跳变系统具有随机特性并且易于建模,当卫星执行器发生跳变故障时可以用Markov跳变理论进行建模。在卫星的相对轨道控制中加入具有Markov跳变性质的控制输入,就可以在可控的情形下对卫星的相对轨道运动进行控制。
综上所述,本文提出了执行器跳变故障的失效卫星轨迹跟踪控制问题,并将所设计的控制器应用于卫星在轨交会任务中,给出了相应的仿真结果与分析。
1 问题描述
考虑在圆轨道运行的卫星,当其执行器发生跳变故障时,描述卫星近距离相对运动模型将变为如下形式

(1)
式中
矩阵中的ω是目标卫星的轨道角速度。d(t)∈L2[0,∞)是扰动信号,M(γ(t))是扰动矩阵。{γ(t),t≥0}表示与执行器故障模态相关的Markov随机过程,该随机过程在有限可数集S={1,2,…,N}中取值,S为故障可能出现的模态集合。故障模态的转移概率Λ为
Pr{γ(t+h)=j|γ(t)=i}=
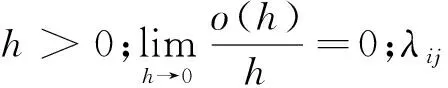
引入如下形式的矩阵来描述卫星执行器的故障情况
F(γ(t))=diag(fi1,fi2,fi3)
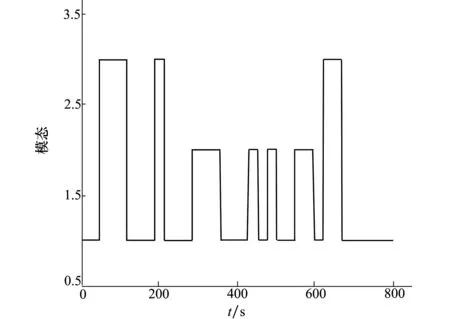
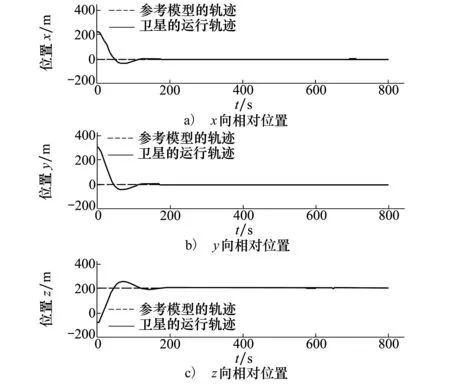
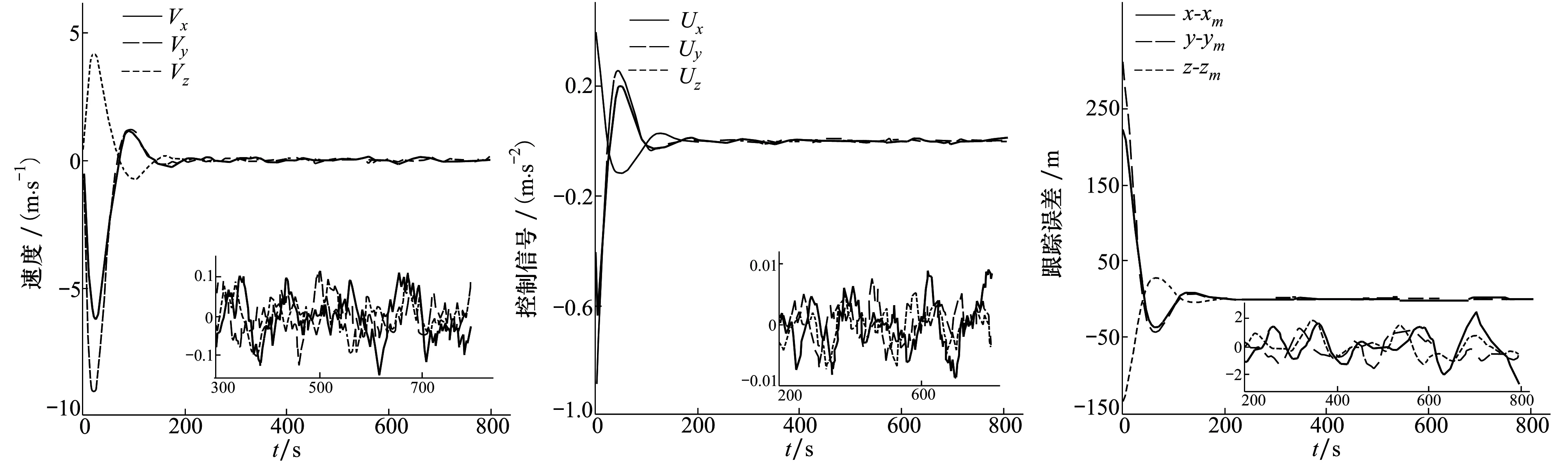
式中:0≤fil≤1,(l=1,2,3分别表示x,y,z方向);当执行器处于模态γ(t)=i时,定义fil=0表示l方向执行器完全失效;0 B(γ(t))=BF(γ(t)) 式中 考虑失效卫星系统(1),在状态反馈控制的作用下,其闭环系统为 (2) 当其故障模态处于γ(t)=i时,为了书写方便记 Ki是使得系统(2)随机稳定的状态反馈增益矩阵。 定义1考虑失效卫星系统(2),若对所有初始条件x(0)=x0和γ(0)=γ0∈S,有不等式 成立,则称系统(2)是随机稳定的。 定义2给定标量r>0,如果对任意非零干扰d∈L2[0,∞),卫星系统(2)是随机稳定的且在零初始条件下,干扰d到输出y的传递函数满足 (3) 成立,则称该系统是随机稳定的并且满足H∞性能指标r。 本文主要研究失效卫星近距离轨迹跟踪控制问题,其要求是闭环系统随机稳定且能够实现对给定信号的跟踪,因此,可将该问题归为一个模型参考跟踪控制问题。通常情况下,参考信号可由以下线性连续参考模型系统生成 (4) 式中:xm(t)∈R3×1和ym(t)∈R3×1分别是参考模型系统的状态向量和输出向量;R表示实空间;Am和Cm是给定的相应维数的系统矩阵。 面向失效卫星的相对轨道跟踪控制问题: 给定失效卫星系统(1)和参考模型(4),设计反馈加前馈形式的控制器 u(t)=Kix(t)+Kmixm(t) (5) 式中,Km(γ(t)=i)=Kmi是前馈补偿器的增益矩阵,使得 1) 卫星系统(2)是随机稳定的; 2) 输出向量y(t)在均方意义下跟踪上参考模型的输出ym(t),也就是对任意初值x(0),xm(0)和γ(0)使得如下不等式成立 文献[9]给出了执行器正常情形下的控制器存在条件,本文将该条件推广到了执行器发生跳变故障情形。以下是执行器发生跳变故障时的控制器存在条件。 推论1控制器有解的充要条件是:在失效卫星系统(2)是随机稳定的前提下,存在矩阵Gi∈R6×3和Hi∈R3×3(i=1,2,…,N)满足下面的矩阵方程组 (6) 则前馈补偿增益矩阵可表示为 Kmi=Hi-KiGi (7) 由控制器的形式(5)可知,需设计状态反馈控制律和前馈补偿器。下面对状态反馈控制律和前馈补偿器分别进行设计。 定理1在卫星系统(2)当中,如果存在一组依赖于故障模态i的矩阵Wi和对称正定矩阵Xi,i=1,2,…,N,满足如下线性不等式成立 (8) 式中: (9) 证明当系统(2)的干扰不为零时,为了得到卫星的H∞性能指标,定义变量Ξ (10) 选取依赖于故障模态i的Lyapunov函数Vi=xTPix,在零初始条件下,由Vi|t=0=0可得 成立。其中 (11) 进一步,考虑到卫星控制中存在输入上限的约束,为保证系统正常工作,定义约束条件 ‖u(t)‖2≤umax (12) 式中,umax是系统的最大控制输入,表示卫星的执行器能够提供的最大加速度。基于输入受限的失效卫星H∞状态反馈控制律由以下定理给出。 定理2卫星系统(2)是H∞随机稳定的并且同时满足(12)式的充分条件是存在一组依赖于故障模态i的对称正定矩阵Xi和一组矩阵Wi,满足如下LMI条件 (13) (14) (15) 式中,ρ为给定的正数。此时,相应的状态反馈控制律的增益矩阵可表示为 (16) 证明关于(15)式和控制器(16)式的证明,定理1已给出证明,这里不再赘述。参照文献[15]中的相关定理直接给出另外2组LMI条件(13)式和(14)式的证明。 对每一个模态i定义一个Lyapunov函数Vi(x(t))=xT(t)Pix(t),考虑输入约束条件(12),假设初始条件满足xT(0)Pix(0)≤ρ,ρ为一个给定正值。则对于t>0有 xT(t)Pix(t)≤xT(0)Pix(0)≤ρ (17) (18) 联合(17)和(18)式,由Schur补引理可以得到 (19) 同样根据Schur补引理,初始条件xT(0)Pix(0)≤ρ可以写为 (20) 在对干扰抑制过程中,总希望有最好的抑制效果,所以在状态反馈控制律的设计过程中,需要在满足定理2中LMI条件的情况下,尽量找到干扰抑制界r的最小值。关于r的求解由以下推论给出。 推论2卫星系统(2)是随机稳定的并且对干扰抑制界r的求解,可转化为如下优化问题: minr (21) 此时状态反馈控制器的增益矩阵可表示为(16)式的形式。 前馈补偿器的作用是满足对给定信号的跟踪。文献[16]通过对非齐次广义Sylvester矩阵方程组的求解,获得了前馈补偿器的参数化表达形式。这部分参照文献[16]当中对前馈补偿器的求解方法,类似地可以得到矩阵Gi和Hi(i=1,2,…,N)的一组参数化通解表达式为 (22) 式中,矩阵Zi∈R3×3是任意参数矩阵,代表参数化通解的自由度。具体求解过程以及(22)式中相关矩阵的定义可以参考文献[16],限于文章篇幅,不再赘述。 本文针对失效卫星所求解的模型参考跟踪控制核心问题就是设计控制器u(t)使其能保证系统是鲁棒H∞随机稳定的,并且能够满足对给定指令的跟踪。接下来给出失效卫星控制器求解的详细算法: 第1步 选取参考模型的参数矩阵Am,Cm以及干扰矩阵Mi; 第2步 求解状态反馈控制律。利用线性矩阵不等式(21),解出最小的干扰抑制界r,以及矩阵Xi和Wi; 第4步 求解前馈补偿器,利用(22)式求解矩阵Gi和Hi; 第5步 由(7)式计算前馈补偿器增益矩阵Kmi=Hi-KiGi。 本文考虑目标卫星运行在地球同步轨道,其轨道参数:轨道周期T=86 164 s,轨道角速度ω=7.292 1×10-5rad/s,半径R=4.224 1×107m。接下来考虑失效卫星的执行器发生跳变故障情形,假定执行器出现以下3种故障模态:①f11=f12=f13=1,表示卫星所有执行器工作正常;②f22=0.85,f21=f23=1,表示卫星在y方向上执行器部分失效,其他方向执行器正常工作;③f33=0.85,f31=f32=1,表示卫星在z方向上执行器部分失效,其他方向执行器正常工作。则跳变输入矩阵Bi可以表示为 转移概率矩阵为 将失效卫星系统中存在的扰动d模拟为白噪声干扰,干扰矩阵取为 接下来选取卫星系统的初始状态值为x(0)=[225 312 -143 0 0 0]T。假定卫星的执行器能提供的最大加速度为umax=3 m/s2。参考模型选取Am=03×3,Cm=I3×3。设置仿真时间800 s,仿真结果如下所示。 图1是卫星系统的执行器随着时间发生跳变故障的3种情形,卫星的执行器随着时间的变化,在3个模态之间进行切换,执行器出现故障的情形具有一定随机性。 图1 执行器的故障模态 图2 卫星相对距离 图2和图3为跟踪卫星和目标卫星的相对位置和相对速度曲线。由图2和图3可知,跟踪卫星和目标卫星相对距离和相对速度在大约前200 s内均大幅度减小。由于初始时刻两卫星间的位置存在偏差,因此卫星在前200 s内以较大的速度进行轨道机动,以消除偏差,随后以约0.1 m/s的速度进行微调,两卫星间相对位置也进一步减小。 图4为卫星所施加的控制信号,由于初始时刻两星相对位置存在较大偏差,因此前200 s内执行机构施加的控制信号较大,随后卫星约以0.01 m/s2的控制信号继续向目标低速缓慢接近。图4说明失效卫星系统(1)和控制器(5)所组成的闭环控制系统是随机稳定的。 图5为位置跟踪误差,由图可知,卫星系统存在白噪声干扰情形下,稳态跟踪误差大约为2 m。这验证了本文所设计的模型参考跟踪控制器的有效性。即本文所设计的控制器能够使得失效卫星完成对给定指令的跟踪。 图3 卫星相对速度 图4 控制信号 图5 跟踪误差 本文讨论执行器故障情形的失效卫星轨迹跟踪控制问题。建立了含有跳变参数的卫星相对运动数学模型,采用跳变系统随机稳定性的充要条件与模型参考跟踪控制思想给出了在随机切换控制下的模型参考跟踪控制器的存在条件,并利用LMI方法和矩阵方程理论提出了失效卫星控制器的设计算法。所设计的控制器中包含自由参数矩阵,可以通过该参数矩阵对控制器进行进一步优化。数值仿真结果表明在失效卫星系统存在白噪声干扰时,所设计的控制器能够快速、准确地完成对给定指令的跟踪。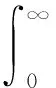
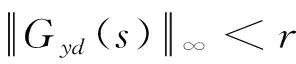

2 主要结果
2.1 模型参考跟踪控制器的存在条件
2.2 鲁棒H∞状态反馈控制律设计
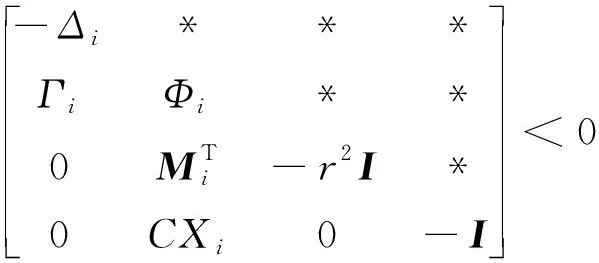
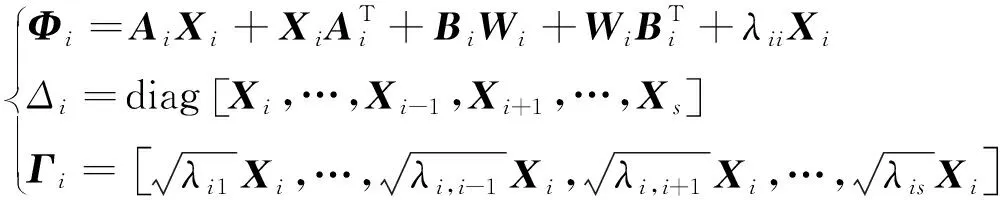
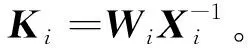
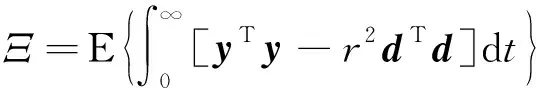
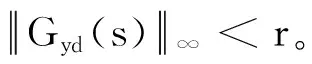

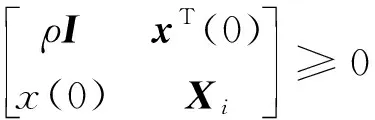
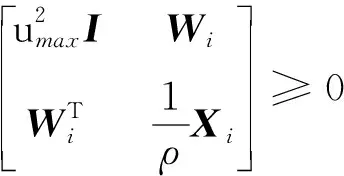
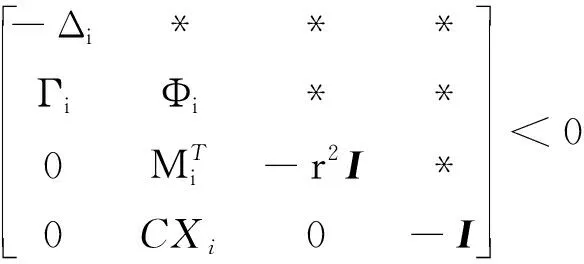

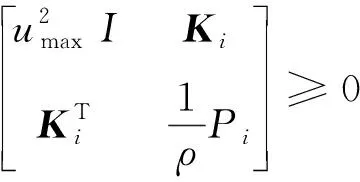
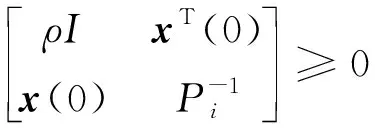
2.3 前馈补偿器的设计
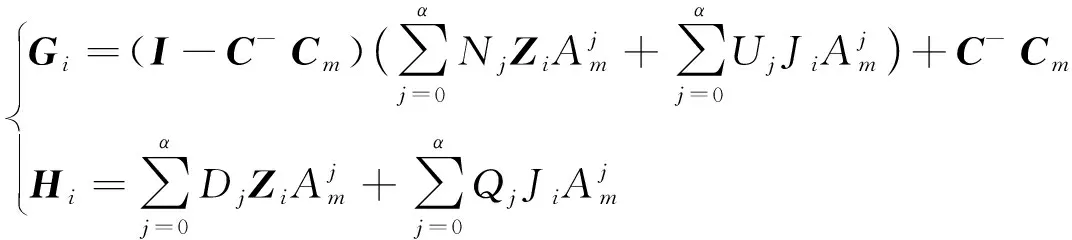
2.4 控制器求解算法
3 仿真校验

4 结 论

