基于改进Funnel控制的机械臂轨迹跟踪约束控制

张 蕾，周嘉欣，黄晨静，王晓华

(1.西安工程大学 电子信息学院，陕西 西安 710600；2.陕西省人工智能联合实验室 西安工程大学分部，陕西 西安 710600)

0 引 言

关节柔性机械臂由于其灵活、轻便、良好的人机交互特性，在医疗、管道检修、反恐侦察、航空航天等领域都发挥着重要的作用。不同于刚性机械臂，由于谐波减速器等元件引入的柔性特性，使得关节柔性机械臂的轨迹跟踪控制设计更为复杂，引起了学者们广泛的关注[1-2]。

关节柔性机械臂的轨迹跟踪控制方法有反馈线性化控制、奇异摄动控制、滑模控制、自适应控制等[3-4]。文献[5-6]分别提出了基于神经网络观测器以及扩张观测器的控制算法；为了获得更高的稳态跟踪精度，文献[7]基于自适应模糊控制算法提出鲁棒最优控制；文献[8]基于重力补偿算法对带有振动的关节柔性机械臂进行位置控制；进一步考虑到存在外部干扰的情况，文献[9]针对带有随机噪声的关节柔性机械臂进行基于事件触发的自适应神经网络位置控制；文献[10]基于干扰观测器结合PD设计控制器；文献[11]基于干扰观测器设计鲁棒最优控制算法；文献[12]采用自适应模糊控制增强系统遭受干扰下的鲁棒性。对于上述文献采用反步法设计控制律的过程中，存在对系统虚拟控制律的反复求导这一计算爆炸问题，已有文献采用动态面法[13-14]、命令滤波法[15-16]及跟踪微分器法[17]等方法应对。但上述控制方法在关节柔性机械臂的轨迹跟踪控制方面只考虑了提高稳态跟踪精度，没有考虑到瞬态预设性能。

预设性能概念由BECHLIOULIS等提出，采用转换函数将有约束的误差系统转换为无约束误差系统[18]。但在实际应用中，由于构造的转换函数具有偏微分项，可能会引起控制器奇异问题[19]。因此,ILCHMANN提出了Funnel控制方法[20]，基于时变的比例增益调节瞬态性能和稳态跟踪误差。文献[21]结合BP神经网络和非奇异终端滑模Funnel控制，保证电机系统的稳态和瞬态性能，但该算法只针对相对阶为一阶、二阶系统。为此，HAN等提出一种改进Funnel控制方法，拓宽了该算法的适用范围[22]。

关节柔性机械臂模型中力矩存在输入饱和问题，饱和非线性特性的存在会影响系统的控制性能、跟踪精度和超调量等。因此，对于饱和非线性特性的研究引起了众多学者的关注[23-25]。综上所述，在考虑到存在输入饱和这一非线性特性的基础上，如何设计控制算法同时保证稳态和瞬态性能是需要继续研究的问题。

本文基于改进的Funnel控制方法，结合最小参数学习法自适应RBF神经网络设计控制策略。采用时变瞬态性能约束函数设计改进的Funnel控制变量，定量调节初始误差值的设定范围和收敛速度，保证了最大超调量在合理范围内。改进的Funnel控制变量避免了控制器中存在微分不可导的情况。针对反步法存在的计算爆炸问题，采用RBF神经网络进行逼近。为了进一步降低神经网络的计算负荷，引入最小参数学习法进行神经网络的权值更新。通过理论证明，关节柔性机械臂控制系统中的所有变量是半全局一致最终有界的。

1 问题描述与算法基础

1.1 关节柔性机械臂数学模型

根据动力学建模所采用的拉格朗日-欧拉方法，考虑关节柔性机械臂连杆侧和电机侧的摩擦力以及电机作为执行机构时存在的输入饱和情况，可以得到单连杆关节柔性机械臂动力学模型[13]，即

(1)

式中：I表示连杆的转动惯量；M表示连杆的质量；g为重力加速度；L为连杆的长度；K为关节柔性系数；J为电机的转动惯量；B为电机侧摩擦系数；q、qm为连杆的位置和电机的位置；u(v)为考虑输入饱和情况下的执行机构-电机的输入力矩。

(2)

(3)

由于状态方程第二阶、第四阶表达式可化简为

(4)

故提出如下假设：

假设1p2和p4为未知常数，q2和q4为未知的连续函数；

假设2 存在yd为n阶可导、连续且有界的光滑函数。

本研究的控制目标是：为关节柔性机械臂动力学模型(1)设计一种轨迹跟踪约束控制算法，使得连杆位置q既可以跟踪既定的轨迹yd，跟踪误差收敛于0的邻域内，同时约束机械臂位置跟踪误差的瞬态性能收敛于给定的Funnel边界内。整个系统的状态变量是半全局一致最终有界的。

1.2 模型饱和特性的线性化

对电机存在饱和这一非线性特性进行线性化处理，采用一个光滑函数近似饱和函数，即

(5)

式中：sat(·)为饱和函数；v表示不考虑饱和的电机输入力矩；u(v)表示电机受到饱和非线性特性影响下的实际输入力矩；uM表示饱和非线性的上下限幅。

(6)

式中：g(v)为本文选择的光滑函数，用于逼近u(v)；s(v)为逼近以后的误差。u(v)和g(v)都为有界函数，g(v)是一个tanh函数，可得s(v)是有界函数，|s(v)|=|u(v)-g(v)|≤S。

1.3 改进的Funnel控制设计

常规的Funnel控制在误差为0时存在不可导点，不满足反步法的设计要求。本文设计改进的Funnel控制使得误差为0时也为可导点，进而满足反步法设计要求。定义函数：

(7)

式中:F1为误差收敛函数；δ0为误差初始值，δ∞为时间趋于无穷时稳态误差值，δ0≥δ∞>0；a0为收敛速度，a0越大误差收敛速度越快；ρ(t)为设计的误差控制增益。由式(7)可知:e1(t)靠近F1(t)则ρ(t)增大；反之则减小。e1(t)越靠近F1(t)则s1越大；反之则越小。F1、e1两者关系如图1所示。

图 1 Funnel控制的基础概念示意图Fig.1 Schematic diagram of the basic concept of Funnel control

从图1可以看出：选取一个误差为正的点e4，误差距离上方蓝色曲线越近，s1越大；选取误差为负的点eB，误差距离下方蓝色曲线越近，s1越大。根据这一原理设计第一阶改进Funnel变量s1。

假设3 误差收敛函数F1为n阶连续、可导且有界函数。

2 算法设计和稳定性分析

2.1 控制律设计

根据本文对于关节柔性机械臂的控制目标，定义跟踪误差：

(8)

式中：αi(i=1,2,3)为基于反步法下引入的虚拟控制函数。为保证每一阶误差子系统的稳定性，逐级考虑误差系统的镇定问题：采用前述改进的Funnel控制约束瞬态性能；采用基于最小参数学习法的自适应神经网络逼近未知函数和反步法步骤中的虚拟控制函数的导数。

步骤Ⅰ:

设计第一阶改进的Funnel变量

(9)

注2 所提出式(9)的s1避免了误差为零时不可导的情况，使得系统满足反步法设计要求。

对改进Funnel变量s1求导,可得

(10)

(11)

式中：常数k1>0。将式(11)代入V1,可得

(12)

注3e2保留在式(12)中，需要将其引入到下一阶误差子系统的镇定控制中。

步骤Ⅱ：

(13)

式中：λ2代表神经网络的逼近误差最大值。考虑到自适应神经网络逐个更新单个权值计算负荷较大，本文采用最小参数学习法进行权值的更新设计，即b2θ2=‖ω2‖2。

对一个神经网络,只需要更新一个数值θ2，即可加快计算时间。采用不等式对e2Q2进行放缩。

注4 常数b2的作用只是用于稳定性分析，不需要给出明确的数值计算结果。

为了镇定第二阶误差子系统，设计第二个虚拟控制律

(14)

对含有第二阶虚拟控制律的e2p2α2进行放缩。基于李雅普诺夫稳定性原理为自适应参数θ2设计自适应律,即

(15)

式中：a2和σ2为待设计的正常数。将式(14)、(15)代入式(13)中，可得

(16)

注5e3保留在式(16)中，需要将其引入到下一阶误差子系统的镇定控制中。

步骤Ⅲ：

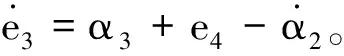
(17)

式中：λ3代表神经网络的逼近误差最大值。考虑到自适应神经网络逐个更新单个权值计算负荷较大，采用最小参数学习法更新设计权值，即θ3=‖ω3‖2。对一个神经网络只需要更新一个数值θ3，即可加快计算时间。采用不等式放缩e3Q3。

为了镇定第三阶误差子系统，设计第三个虚拟控制律：

(18)

对式(18)中含有第三阶虚拟控制律的e3α3进行放缩。基于李雅普诺夫稳定性原理为自适应参数θ3设计自适应律:

(19)

式中：a3和σ3为待设计的正常数。将式(18)、(19)代入式(17)中，可得

(20)

注6e4保留在式(20)中，需要将其引入到下一阶误差子系统的镇定控制中。

步骤Ⅳ：

最终设计

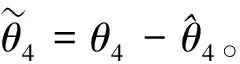
(21)

采用自适应RBF神经网络进行逼近，定义

式中λ4代表神经网络的逼近误差最大值。考虑到自适应神经网络逐个更新单个权值计算负荷较大，采用最小参数学习法更新设计权值，即b4lθ4=‖ω4‖2。对一个神经网络只需要更新一个数值θ4，即可以加快计算时间。采用不等式对e4Q4进行放缩。

注7 式(21)中，常数b4,l的作用只是用于稳定性分析，不需要给出明确的数值计算结果。

为了镇定整个误差系统，设计实际控制律:

(22)

对含有实际控制律的p4e4h(v)v进行放缩，对于存在输入饱和部分进行放缩处理。基于李雅普诺夫稳定性原理,为自适应参数θ4设计自适应律：

(23)

式中：a4和σ4为待设计正常数。将式(22)、(23)代入式(21)中，可得

(24)

2.2 稳定性分析

对于式(24)中自适应律部分，采用杨氏不等式进行放缩，有以下不等式成立：

(25)

整个误差系统的李雅普诺夫函数为

根据所设计的虚拟控制律式(11)、(14)、(18)和实际控制律式(22)及所设计的自适应律式(15)、(19)、(23)、(25)可以得到

(26)

式中：

ρ=min(2k1,2b2k2,2k3,2b4lk4,σ2,σ3,σ4)

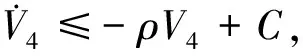
(27)

可以得到不等式

(28)

式(28)的收敛域为

(29)

注8 半全局意味着只能从部分初始状态收敛到有限范围内。关节柔性机械臂系统初始状态是有一定物理限制的，可满足半全局要求。关节柔性机械臂系统的初始状态为

V4中的各状态量是一致最终有界的，可以得到各阶子系统的跟踪误差ei(i=2,3,4)和自适应参数θi(i=2,3,4)是有界的，假设文中跟踪的轨迹yd也是有界的。因此,虚拟控制律式(11)、(14)、(18)和实际控制律式(22)也是有界的，可以得到式(8)中各状态变量xi也是有界的。由此,可以证明系统所有变量是半全局一致最终有界的[26]，并且跟踪误差e1收敛于所设计的Funnel边界函数内，可以保证轨迹跟踪过程中误差的瞬态性能和稳态性能。

3 仿真验证

为了验证设计算法的有效性，在相同的关节柔性机械臂轨迹跟踪任务下，分别与基于常规Funnel控制的自适应神经网络设计算法m2[22]、自适应反步RBF神经网络算法m3[27]及基于tan型障碍李雅普诺夫函数m4[28]进行轨迹跟踪性能对比。在保持控制器参数和跟踪轨迹条件一致的情况下，仿真示例1的仿真参数设定如下：

yd=0.5(sint+sin(0.5t)),a2=a3=a4=0.51

r2=r3=r4=5,σ2=0.2,σ3=σ4=0.1

(x1(0),x2(0),x3(0),x4(0))=

(0.1,0.1,0.2)

k1=5,k2=k3=7,k4=3

[-1,1]×[-5,5]×[-1,1]×[-1,1]×

[-1,1]×[-3,3]×[-1,1]×[-1,1]，

[-1,1]×[-5,5]×[-10,10]×[-1,1]×

[-1,1]×[-1,1]×[-1,1]×[-3,3]×

[-1,1]×[-1,1]×[-1,1]×[0,20]，

[-1,1]×[-5,5]×[-10,10]×[-20,20]×

[-1,1]×[-1,1]×[-1,1]×[-1,1]×

[-1,1]×[-3,3]×[-1,1]×[-1,1]×

[-1,1]×[-1,1]×[0,20]×[0,20]

关节柔性机械臂的系统模型参数满足实际物理意义。最终设计的参数给定如下：

仿真结果如图2所示。

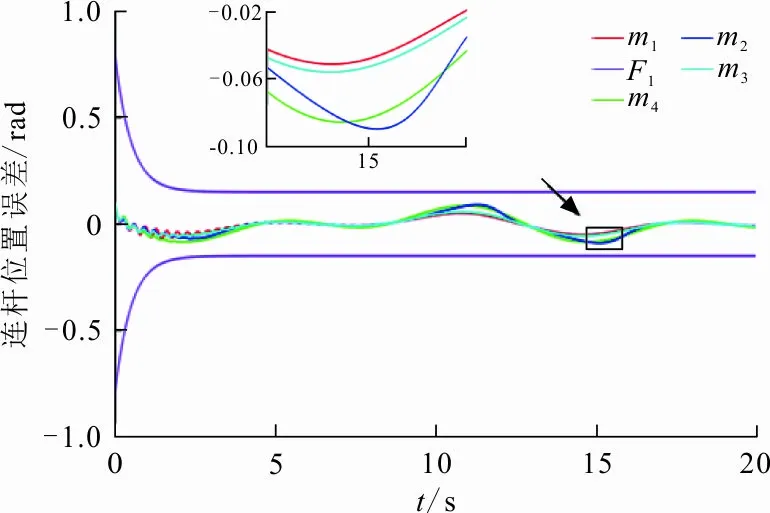
图 2 轨迹跟踪位置误差e1响应曲线

由图2可知：所提方法m1响应曲线有最小的超调量。暂态超调量和基于常规Funnel控制方法m2相比减小43.2%;和没有考虑预设性能函数的自适应神经网络反步法m3相比减小7.9%;和基于tan障碍李雅普诺夫函数的m4相比减少了41.1%。瞬态误差都约束在设计的F1约束性能函数中，没有超过边界。可见，所提算法设计的控制律可以使被控系统有更小的超调量。

图3分析所提方法m1的跟踪轨迹精度。从图3可以看出：和基于常规Funnel控制方法m2相比，m1的精度提高了3%；和没有考虑预设性能函数的自适应神经网络反步法m3相比，提高了0.5%；和基于tan障碍李雅普诺夫函数的m4相比，提高了4.2%。可见，所提算法的稳态精度也高于其他算法。

图4为连杆速度x2、电机位置x3及电机速度x4的响应曲线。

(a) 连杆速度x2

(b) 电机位置x3

(c) 电机速度x4图 4 x2、x3及x4的响应曲线Fig.4 Response curve of x2,x3 and x4

由图4可见，关节柔性机械臂的系统变量x2,物理意义为机械臂的速度,是有界的。由于跟踪的机械臂位置为周期性变化，速度为其导数，因此也是周期性变化的。从图4(a)可以看出：相较于没有考虑瞬态性能的方法m3，所提方法的速度变化更为平缓。在进入10 s以后，神经网络学习到足够的系统状态信息，速度也开始周期性稳定变化。关节柔性机械臂的系统变量x3，物理意义为电机的位置，是有界的。对于电机来说，电机的转动的角度即为电机的位置变化。由于跟踪的机械臂位置为周期性变化，而电机的转动角度和机械臂位置是由弹簧连接，因此电机角度也是周期性变化的。从图4(b)可以看出:相较于没有考虑瞬态性能的方法m3，所提方法的电机角度变化更为平缓。在进入10 s以后，神经网络学习到足够的系统状态信息，电机位置也开始周期性稳定变化。关节柔性机械臂的系统变量x4，物理意义为电机的速度，同样是有界的。由于电机位置为周期性变化，电机的速度为其导数，因此电机速度也是周期性变化的。从图4(c)可以看出：相较于没有考虑瞬态性能的方法m3，所提方法的电机速度变化更为平缓。在进入10 s以后，神经网络学习到足够的系统状态信息，电机速度也开始周期性稳定变化。由于轨迹误差减小，电机速度也随之减小到0上下波动。

仿真示例2:yd=sint，r2=r3=r4=15，k1=6,k2=7.3，k3=7,k4=5.5，其他设计参数和仿真示例1相同。

图5为轨迹跟踪误差e1的响应曲线。

图 5 轨迹跟踪位置误差e1响应曲线Fig.5 Response curve of tracking position error e1

由图5可知：跟踪轨迹为正弦信号时，所提算法的和其他算法相比较超调量更小。暂态超调量和基于常规Funnel控制的方法m2相比，减小31.7%；和没有考虑预设性能函数的自适应神经网络反步法m3相比，减小8.2%；和基于tan障碍李雅普诺夫函数的m4相比，减小了48.2%。瞬态误差都约束在设计的F1约束性能函数中，没有超过边界。

图6为连杆位置x1响应曲线。从图6可知：所提方法m1的跟踪轨迹的精度和基于常规Funnel控制的方法m2相比，提高了1.8%；和没有考虑预设性能函数的自适应神经网络反步法m3相比，提高了0.4%；和基于tan障碍李雅普诺夫函数的m4相比，提高了3.9%。

图 6 连杆位置x1响应曲线Fig.6 Response curve of link position x1

(a) 仿真示例1

(b) 仿真示例2图 7 神经网络自适应参数θFig.7 Neural network adaptive parameters θ

图7(a)为仿真示例1自适应神经网络的自适应参数，图7(b)为仿真示例2神经网络的自适应参数。Q2、Q3、Q4等3个神经网络的自适应参数也都是有界的。随着神经网络学习到足够的信息，输入向量周期性变化，权值也趋于稳定的周期性变化。

(a) 仿真示例1

(b) 仿真示例2图 8 输入饱和情况下力矩u响应曲线Fig.8 Response curve of torque u under input saturation condition

图8为考虑输入饱和情况下电机输入力矩u的响应曲线。所提方法m1中，v表示不考虑饱和的电机输入力矩，u(v)表示电机受到饱和非线性特性影响下的实际输入力矩。经过中值定理和输入饱和函数的处理，可以使得实际输入力矩为u。仿真示例1中输入力矩u受限于±9.5 N·m之间，见图8(a);仿真示例2中u受限于±20 N·m之间,见图8(b)。证明了输入饱和影响下所提算法的有效性。

4 结 语

针对同时存在输入饱和和输出约束的关节柔性机械臂系统的轨迹跟踪问题，提出了一种改进的Funnel控制方法。该方法在跟踪过程中对机械臂误差的瞬态性能可以定量地约束，同时简化了控制器设计。通过李雅普诺夫稳定性理论,证明了所提的方法可以保证闭环系统所有变量是半全局一致最终有界的，跟踪误差收敛于给定的Funnel边界内。相较于其他的暂态性能约束算法，本文所提算法具有更高的稳态跟踪精度和更小的超调量。在今后的工作中将会考虑有限时间控制下的机械臂轨迹跟踪控制。