基于地震观测数据的结构损伤水平表征参数研究

杨永强，杨耀鑫，杨 游，左占宣，公茂盛

（1.中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨 150080；2.地震灾害防治应急管理部重点实验室，黑龙江哈尔滨 150080；3.中国市政工程中南设计研究总院有限公司，湖北武汉 430010）

引言

根据地震发生后第一时间获得的数据判断结构损伤程度是实施应急救援行动关键依据，随着现代传感技术、信号采集与处理和信息融合技术的不断发展，利用传感器采集到的信息对结构的损伤进行识别的方法有了很大的进展。1995年阪神地震发生后，日本建筑研究所在日本主要城市的80栋典型建筑物上布设了密集强震动观测仪器；我国从20世纪70年代起，陆续在一些重要结构如大坝和核电厂等布设了地震反应观测台阵，并陆续在中国地震局办公楼、深圳地王大厦和上海中心等结构设立了地震反应观测台阵。因此如何利用我国现有并不断建设的强震与烈度速报台网、工程结构反应台阵等收集到的数据，在震后快速评估结构损伤是地震工程领域面临的重要挑战之一。而结构在地震作用下动态参数如加速度、变形反应水平以及结构自振频率变化等能提供结构的整体信息，结合合理的基于强震动观测数据的工程结构损伤评估技术，震后快速对结构损伤程度进行识别是可行的。

使用结构动力响应参数来识别结构损伤程度已有众多学者进行过研究，Cawley等［1］最先提出了通过测量结构自振频率的改变来评估结构损伤状态，实现了对二维平面结构损伤的检测；Lam等［2］基于损伤特征匹配技术，利用结构振型的变化识别出二层钢框架结构的损伤位置；Ren等［3］提出了一种基于结构自振频率和振型变化的损伤识别技术，将受损后的特征值方程与结构受损模态相乘并求解方程，成功将此方法应用于梁的损伤识别上；Farrar等［4］将基于振动特性变化的损伤识别描述为一种统计模式识别，并提出了系统性的步骤运用在柱的损伤识别上；刁延松等［5］提出了基于AR模型和因子分析的损伤识别方法，利用加速度响应识别出4层钢框架损伤发生的位置，实现了不利用有限元模型的情况下对结构进行实时监测；常军等［6］利用桥梁的曲率模态结合随机子空间方法，成功识别出桥梁的损伤程度。以上研究都证明了基于结构动力响应参数的损伤识别方法的可行性，但以上研究有以下2个不足之处：（1）大多数都只研究了单一参数与结构损伤之间的关系，并未对比不同参数与结构损伤之间相关性的强弱，且未考虑多个参数组合进行损伤预测；（2）大多数应用在简单的梁柱构件或者桁架结构，只能给出结构构件的损伤相对程度，无法具体量化整体结构损伤程度，因此这些方法是否适用于整体RC框架结构有待进一步验证。

针对现有研究的不足，文中根据9个数值算例的非线性时程分析所得结果，计算出最大层间位移角、结构自振频率相对改变量和结构顶层加速度放大系数相关参数，并计算出结构整体的损伤指数以具体量化结构损失程度。采用数值拟合的方法研究了以上参数与结构损伤指数的相关性，并给出了它们拟合公式和拟合曲线。在此基础上针对位移角数据获取困难的问题，文中给出了一个组合结构体系参数，使用此组合参数在震后可以仅利用收集的结构加速度数据对整体结构进行快速地损伤评估，并且该组合结构体系参数与结构损伤指数的相关性优于组合前的单参数。

1 基础数据

1.1 结构损伤指数与加权方法

结构损伤指数通过与结构损伤相关的参数计算得来，如变形、能量、强度或刚度退化等。用D来表示损伤指数，D为一个无量纲参数，D=0即结构未损伤，D≥1表示结构已完全破坏或倒塌，因此可以根据结构损伤指数的大小来判断结构或构件的损伤程度。

由于使用单一参数对结构整体进行损伤评估会导致结果出现较大地误差［7］，因此国内外学者根据历次地震震后资料和实验模拟提出了许多损伤模型，杨游等［8］对不同损伤模型进行了验证及对比，表明Park-Ang模型对结构损伤的评估较为合理。因此文中选取Park等［9］提出的基于构件变形和耗能线性组合的损伤模型计算构件损伤指数，利用改进的杜修力加权方法加权得到结构总体损伤指数。

1.2 结构有限元模型

参考《混凝土结构设计规范》［10］设计了9个不同层数和设防烈度的RC框架结构，结构的立面图如图1所示，各层层高均为3.3 m，梁、柱的混凝土强度为C30，截面配筋的强度为HRB400，箍筋为HPB300，具体结构信息和配筋如表1所示，其场地类别为二类场地，设计地震分组为第2组。

图1 框架模型立面图Fig.1 Elevations of frame structures（unit：mm）

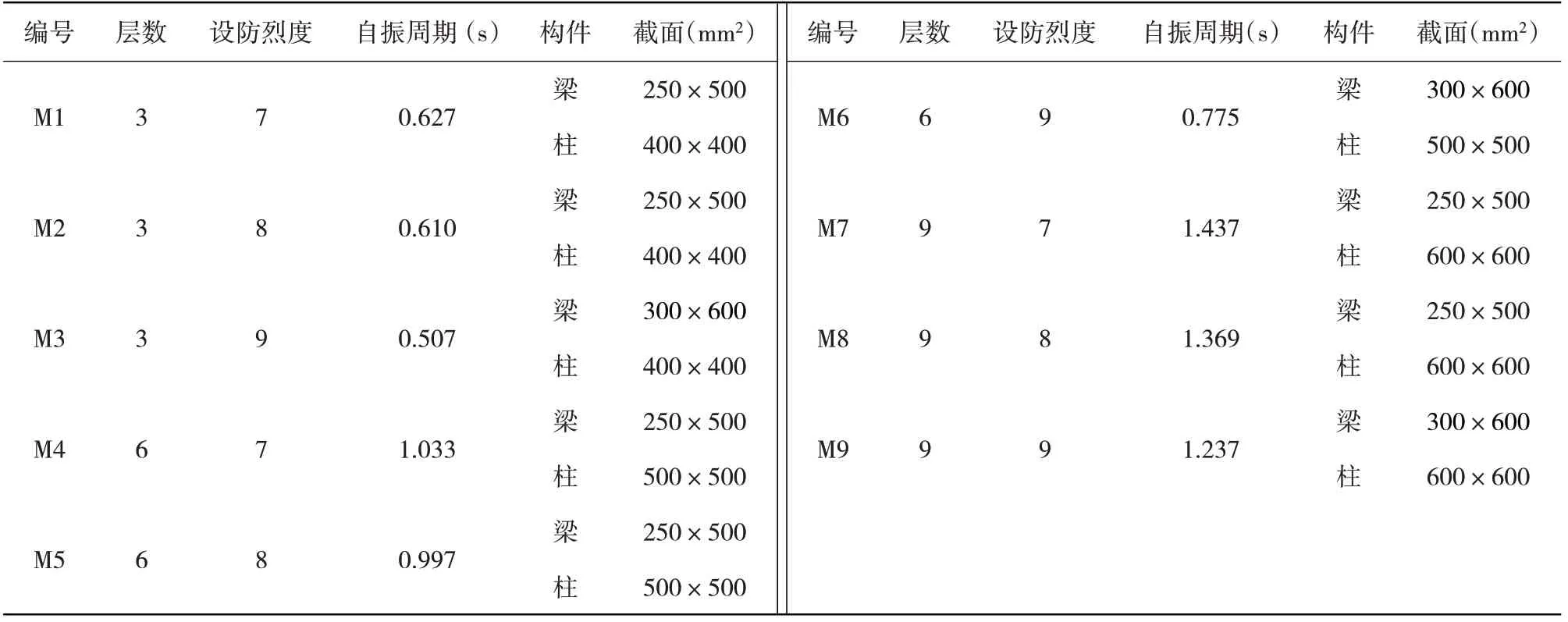
表1 有限元模型设计参数Table 1 Design information of finite element model

使用OpenSees［11］对9个结构的一榀框架建模，其中梁柱单元选用非线性梁柱单元nolinearBeamColumn单元，以在分析中考虑结构的P-Delta效应。柱、梁混凝土强度等级C30，混凝土的本构模型选用Concrete01材料，此材料是以单轴受压本构模型为骨架曲线，且不考虑混凝土的抗拉强度。混凝土的峰值抗压强度取20.1 MPa，峰值压应变为0.001 64。钢筋的本构模型选用Steel02材料，因其能较好地反映钢筋的单轴各向同性的特征且考虑了Bauschinger效应。钢筋的屈服强度取400 MPa，初始弹性模量取206 000 N/mm2，应变强化率取18。梁、柱构件的箍筋约束核心区混凝土的本构模型采用Mander箍筋约束混凝土的应力-应变关系模型［12］，用以计算约束后混凝土的峰值点和极限点处的应力和应变值，定义极限强度为4.02 MPa，极限应变为0.003 8。

1.3 有限元分析及数据的生成

基于郭锋等［13］提出的方法，从PEER NGA-west2地震动数据库挑选出对应于我国规范Ⅱ类场地条件地震动，并与《建筑抗震设计规范》［14］中的强震记录选取方法进行二次筛选，选出100条符合条件的水平地震动。由于天然地震动中，能使结构造成严重破坏甚至倒塌的比例较低，大部分数据集中在结构无损伤和轻微损伤工况，不利于后续相关性的研究。因此调整地震动的PGA以使结构的破坏状况相对均匀分布在无损伤至倒塌工况，此方法已经得到广泛地认可［15］。利用OpenSees［11］有限元软件，输入调幅后的地震动，对上述9个框架结构进行非线性时程分析。并根据有限元计算所得的动力参数，采用1.1节方法计算出不同工况下的结构损伤指数。

2 结构损伤指数与单参数的关系

2.1 结构损伤指数与最大层间位移角的线性回归

最大层间位移角通常被认为是判断钢筋混凝土结构在震后损伤程度的可靠指标，因为结构在地震作用下进入弹塑性状态后，位移量的改变速度远大于力的增长速度，使用基于位移的参数来识别结构的损伤程度是合理的［16］，最大层间位移角已经在许多研究中被用于评估结构的非弹性响应［17-19］，是目前用来判断框架结构损伤程度应用最广泛的指标。文中根据对9个结构有限元分析的结果发现结构损伤指数与最大层间位移角近似线性相关，因此提出拟合公式分别对9个结构的结构损伤指数和最大层间位移角进行线性拟合：

式中：D为结构损伤指数；θ为最大层间位移角；k1，k2为待定系数。计算得拟合系数见表2，拟合直线见图2。

表2 结构损伤指数与结构最大层间位移角的拟合Table 2 The fitting of structural damage index and the maximum inter-story drift

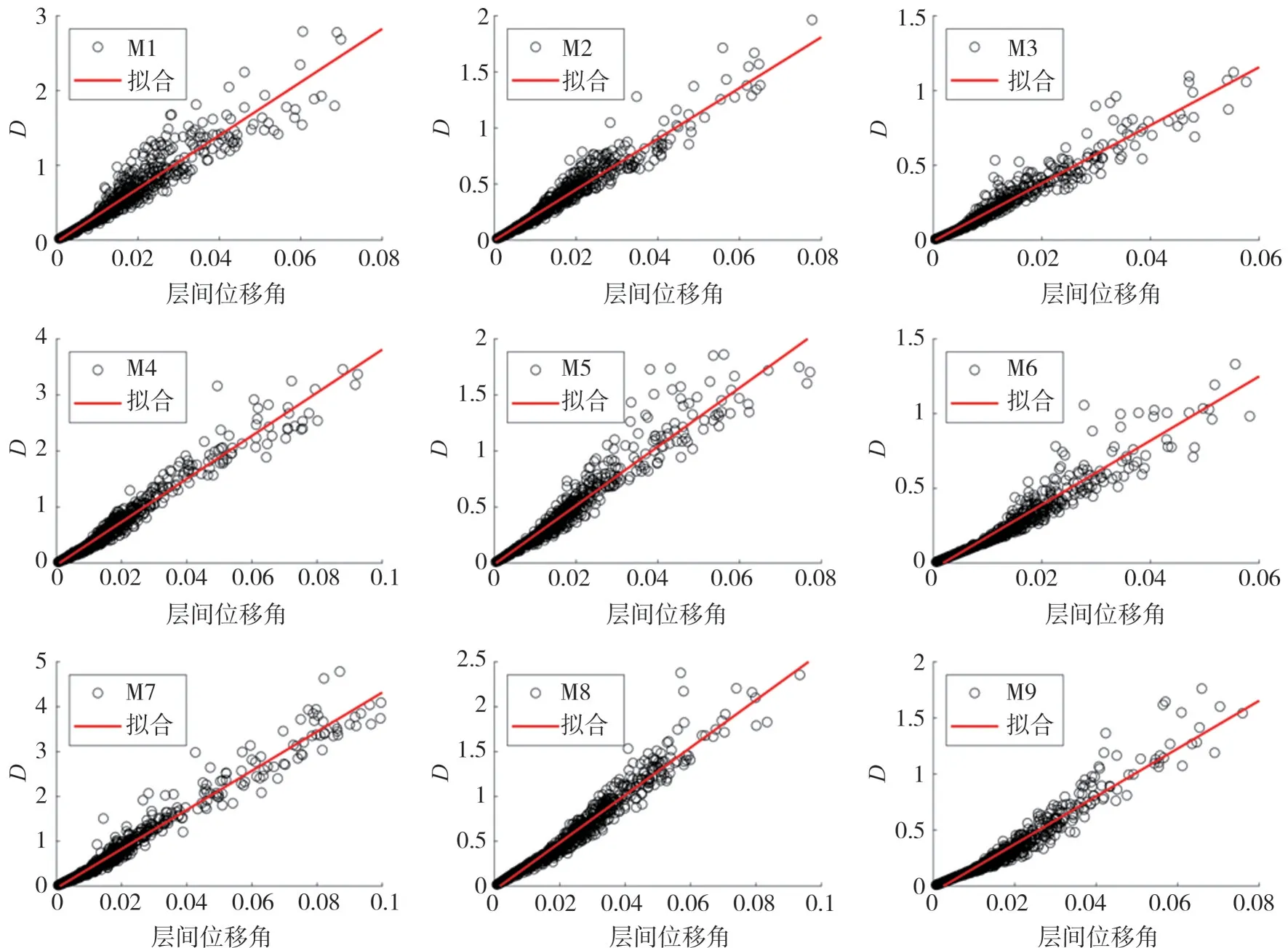
图2 结构损伤指数与最大层间位移角的拟合图Fig.2 Fitting diagram of structural damage index and the maximum interlayer displacement angle

文中采用Pearson相关系数r对拟合效果进行评价，Pearson相关系数变化范围为[ -1,1]，r为正数时表示正相关，r为负数时表示负相关，汪东华［20］将Pearson相关系数划分为极弱或不相关、低度相关、中度相关和高度相关4类，具体评价标准见表3。

表3 相关系数的分类Table 3 Classification of correlation coefficients

从表2和图2可以得出以下结论：（1）损伤指数和结构的最大层间位移角之间关系为正相关，并且9个结构得出的相关系数都表明结构损伤指数和最大层间位移角的相关性为高度相关；（2）从图2可以看出离散点都分布在拟合直线附近，证明了最大层间位移角是识别结构损伤的良好指标。

2.2 结构损伤指数与结构频率相对改变量的回归

由2.1节分析可知结构最大层间位移角与结构损伤指数相关性较大，但在实际对结构监测过程中，获得准确的结构层间位移数据比较困难，强震监测仪器获取的加速度数据在实际工程中容易获得且更为可靠［16］。结构损伤后一般情况下质量和刚度都会发生改变，自振频率作为反映结构自身性质的敏感性指标，被广泛地用于各种结构的健康监测。根据Salawu等［21］对使用频率变化进行损伤识别的总结，频率变化能较好地对反映结构整体损伤情况，因此考虑通过地震前后结构第一振型频率变化来识别损伤。文中采用公茂盛等［22］提出的从结构顶层加速度数据识别结构自振频率的方法，计算出结构震前后结构第一振型频率变化，此方法经过验证表明识别出结构的自振频率与实验获得的自振频率相比误差很小，结果可靠。频率相对改变量如式（2）所示，为归一化的频率参数，本节分析结构损伤指数与频率相对改变量的关系。

式中：Δf为频率相对改变量；f u为地震作用前的结构自振频率；f d为地震作用后的结构自振频率。

参考公茂盛［22］对结构损伤指数和结构体系参数的研究，提出一个三次多项式来拟合结构损伤指数和频率相对改变量之间的关系：

式中，k1、k2、k3、k4为待定系数；其余同式（1）、式（2）。

计算出的M1-M9的待定系数和相关系数见表4，拟合曲线见图3.

从表4和图3中可以得出以下结论：（1）总体上看结构损伤指数与结构第一振型频率相对改变量成正相关，相关系数中位值为0.60，基本可以认为二者中度相关。但在结构M3和M7上，离散点较多，相关性仅为低度相关；（2）从图3可以看出频率相对改变量在0～0.3之间时，点大多都在拟合曲线附近，但在其从0.3增加到0.5的过程中，离散点较多，拟合效果较差。综上不建议单独使用结构自振频率相对改变量对结构损伤指数进行判断，否则会导致较大的误差。

图3 结构损伤指数与频率相对改变量的拟合图Fig.3 Fitting diagram of structural damage index and relative frequency change

表4 结构损伤指数与频率相对改变量的拟合Table 4 The fitting of structural damage index and relative frequency change

2.3 结构损伤指数与顶层加速度放大系数的回归

式中，S为结构顶层加速度放大系数，其余同式（3）。计算得拟合系数见表5，拟合曲线见图4。

图4 结构损伤指数与顶层加速度放大系数的拟合图Fig.4 Fitting diagram of structural damage index and acceleration amplification coefficient of the top floor

表5 结构损伤指数与顶层加速度放大系数的拟合Table 5 The fitting of structural damage index and acceleration amplification coefficient of the top floor

从表5和图4中可以得出结论：（1）总体上看结构损伤指数与顶层加速度放大系数为负相关，相关系数的中位值为-0.76，因此相关性为中度相关；（2）顶层加速度放大系数在0到4之间存在较多离散点，但总体上看数据点基本分布在拟合曲线的周围，且在结构损伤指数小于1时拟合效果良好。

3 组合结构体系参数

由以上分析可知，结构损伤指数和最大层间位移角的相关性为高度相关，而与频率相对改变量和顶层加速度放大系数都为中度相关，且存在较多与拟合曲线偏离的离散点，因此单独用频率相对改变量或者顶层加速度放大系数去识别结构损伤指数效果并不理想。但是在实际监测中，如果使用布置大量位移计的方法来获得最大层间位移角数据，需要耗费大量的金钱和人力［24］，且不能方便地重复使用［25］；如使用加速度数据积分来推导位移数据，受到传感器噪声和边界条件的限制，结果并不精确［26］。而使用加速度传感器获得的加速度数据更易获得且更准确［27］，此外随着智能手机的普及，公众收集到的加速度数据在震后损伤识别中也能发挥更加积极的作用［28］。值得一提的是，文中的频率相对改变量和顶层加速度放大系数都为使用顶层加速度数据推导而来，因此在实际工程比最大层间位移角更易获得。

基于此原因文中提出组合结构参数x，x由频率相对改变量和顶层加速度放大系数组成，尝试使组合结构体系参数x与结构损伤指数的相关性比单参数更好。通过相关性分析及多次试算，提出如下的组合结构体系参数：

式中：x为组合结构参数；Δf为结构自振频率相对改变量；S为结构顶层加速度放大系数；k1、k2、k3为待定系数。

同样采用三次多项式拟合结构损伤指数和组合结构参数x之间的关系，拟合公式如下：

式中：D为结构损伤指数；x为组合结构体系参数；a1、a2、a3、a4为待定系数。组合公式待定系数、拟合公式待定系数及相关性系数见表6，拟合曲线见图5。

图5 结构损伤指数与组合参数的拟合曲线Fig.5 Fitting diagram of structural damage index and combination parameters

表6 结构损伤指数与组合参数的拟合Table 6 The fitting of structural damage index and combination parameters

同时为了更好地比较组合结构参数和单独参数的拟合效果，引入均方误差函数MSE（mean squared error，MSE）：MSE=。式中，N为样本总量，y i为拟合值，x i为真实值，‖·‖为2-范数，即为预测值与真实值之间的距离。组合结构体系参数的相关系数和单参数的对比见表7，均方误差的对比见表8。

表7 不同参数的相关系数对比Table 7 Comparison of correlation coefficients of different parameters

表8 不同参数的均方误差函数对比Table 8 Comparison of mean squared error of different parameters

从表6、表7、表8和图5可以得出以下结论：

（1）结构损伤指数与组合结构体系参数成正相关，9个结构相关系数的中位数为0.80，可以认为组合结构参数与结构损伤指数高度相关；

（2）从表7和表8可以看出，提出的组合结构参数与结构损伤指数的相关性在9个结构上都要优于单参数，9个结构单独的均方差和平均均方差也小于单参数。说明相比频率相对改变量和顶层加速度放大系数，组合结构参数与结构损伤指数的相关性更好，拟合值的方差更小；

（3）从图5点的分布可以看出在结构损伤指数在［0，1］时相关性较强，在此范围内除了极少部分离散点外大部分点都靠近在拟合曲线上。在破坏程度更大时，即结构损伤指数大于1时，点的离散程度显著增加，说明式（6）的拟合精度下降，然而此时结构的破坏程度已处于倒塌状态，在这种情况下识别的结构损伤指数的精度不重要［18］，能判断出结构处于倒塌状态已经能满足震后损伤快速评估的要求。

4 结论

文中设计了9个钢筋混凝土框架结构，并分析了结构在地震作用后的损伤指数与结构在地震作用下动力响应参数之间的相关性，对结构损伤指数与结构最大层间位移角、频率相对改变量和结构顶层加速度放大系数的关系进行了回归分析。由于目前在地震作用下准确地获得结构的位移数据需要布置大量的位移传感器，且维护困难需要耗费大量的人力及物力，使用最大层间位移角来识别结构的损伤程度在某些情况下具有局限性。因此基于结构频率相对改变量和结构顶层加速度放大系数提出了一个组合结构体系参数，建立了一个组合结构体系参数与结构损伤水平的关联模型。文中主要得出以下结论：

（1）结构损伤指数与最大层间位移角高度正相关，最大层间位移角是识别结构损伤的良好指标，如果在震后能获得准确的最大层间位移角数据即可较好地用于预测结构震后损伤程度。

（2）结构自振频率相对改变量与结构损伤指数正相关，结构顶层加速度放大系数与结构损伤指数负相关，通过相关性分析，可以认为二者都为中度相关，因此不建议单独使用结构自振频率相对改变量或者结构顶层加速度放大系数对结构整体损伤程度进行识别。

（3）文中提出了一种基于频率相对改变量和顶层加速度放大系数的组合结构体系参数，与结构损伤指数高度相关，相关性和误差均优于组合前的单参数。且计算所需要的加速度数据在实际工程中易于获得，可用于在震后对平面布局规则的非高层框架结构损伤进行快速评估。

文中以RC框架结构研究对象，探讨了结构损伤指数与最大层间位移角、自振频率相对改变量和顶层加速度放大系数之间的相关性，并以结构自振频率相对改变量与顶层加速度放大系数来建立组合结构参数，未来可针对多种结构类别及更多的结构动力参数，进行更全面地研究。