考虑行波效应的高聚物注浆修复埋地排水管道地震反应分析

徐建国，陈志豪，王 壬，徐一鸣

（1.郑州大学水利科学与工程学院，河南郑州 450000；2.中水东北勘测设计研究有限责任公司，吉林长春 130000；3.机械工业第六设计研究院有限公司，河南郑州 450000）

引言

高聚物注浆修复技术通过向管道结构脱空渗漏处注射高聚物注浆材料来达到填充脱空、封堵渗漏和抬升沉降管道的目的，作为一种微创高效的地下管道非开挖修复技术，目前该技术已成功应用于多种地下管道修复工程项目中［1-3］。对于高聚物修复管道的地震响应也有学者进行了相关研究［4-6］，但上述研究采用的地震输入均为一致激励。对于小跨度结构来说，不考虑地震动的空间变化是合理的，然而研究表明，对于管道等大跨度结构采用一致激励的地震输入不符合实际情况，可能会导致抗震设计的不合理［7-8］。因此对于高聚物注浆修复地下排水管道进行非一致激励地震响应分析是十分必要的。

地震动的差异性包括时间和空间上的差异，主要有行波效应，局部场地效应和部分相干效应等，以行波效应为主［9］。因此文中将主要考虑行波效应下高聚物修复管道的动力响应，依据弹性地基梁理论建立考虑行波效应的高聚物修复管道振动方程，地震输入采用人工生成的随机地震波，进而分析不同视波速对于行波效应的影响。

1 行波效应下高聚物修复管道振动方程求解

对于高聚物修复管道在行波效应下的动力响应问题，文中将地下管道假定为弹性地基上的无限长均质长梁，结合作者之前提出的管-土-高聚物相互作用分析模型［10］，忽略管道内部阻尼，得到高聚物修复管道地震响应计算模型。如图1所示。

图1 高聚物修复管道地震响应计算模型Fig.1 Seismic response calculation model of polymer repair pipeline

1.1 管道纵向振动反应方程求解

地下连续管线通常很长，当实际计算时，可取其中一段管段来计算，当计算管段长度取得足够大时，边界条件对计算管段中间部分的影响就很小，可将计算管段看作自由边界，当管道产生纵向振动时，其计算模型和边界条件如图2所示。

图2 管道纵向振动计算模型和边界条件Fig.2 Pipeline longitudinal vibration calculation model and boundary conditions

假设地下管道周围介质沿管轴线方向分布均匀，则管道纵向振动方程如式（1）所示：

式中：m为管道质量；c为周围介质阻尼系数；k为周围介质纵向刚度；EA为管道的轴向刚度；u(x,t)为管道纵向位移；u g(x,t)为纵向地面位移。

对式（1）振动方程进行求解时，采用拟静力位移法［11］来考虑行波效应的影响，将式（1）中的管道纵向位移u(x,t)进行分解，如式（2）所示，分别是由地面运动引起的拟静力位移u s(x,t)和由结构惯性和阻尼引起的动态位移ud(x,t)。

去掉式（1）中的动态项，得到拟静态位移常微分方程如式（3）所示：

式（3）所对应的齐次方程的通解为：

将场地位移和管道位移在区间（0，l）上展开为余弦级数，从而可得式（3）的特解为：

将式（4）和式（5）相加并代入边界条件可得微分方程的解为：

然后将式（1）中的动态项提出，可得：

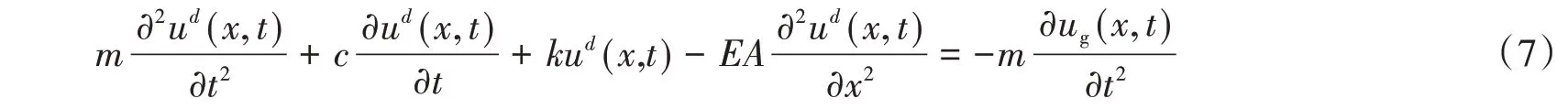
对于动态位移可以采用振型叠加法［12］求解，首先在式（7）中去掉阻尼项和非齐次项，利用分离变量法，代入边界条件，可得自振频率和振型如下：

然后令

将上式代入方程（7）中，可得：

利用振型叠加法对式（11）解耦：

两端同时在区间（0，l）上积分，根据振型正交性，可得：

计算时可取前N个振型，求出对应的qn(t)后根据式（10）可近似求出动态位移如式（14）所示：

最后将拟静态位移和动态位移相加，即可得到行波效应下管道纵向振动方程的位移解，由位移可进一步得到管道的应变及内力。

1.2 管道横向振动反应方程求解

管道横向振动计算模型和边界条件如图3所示，横向振动方程为：

图3 管道横向振动计算模型和边界条件Fig.3 Pipeline lateral vibration calculation model and boundary conditions

虽然纵向振动和横向振动的运动方程和边界条件均不同，但求解思路相同，因此这里就不再赘述，按上述纵向振动中的替换为，即可得到横向振动拟静力位移为：

相应的其求解q n(t)的微分方程为：

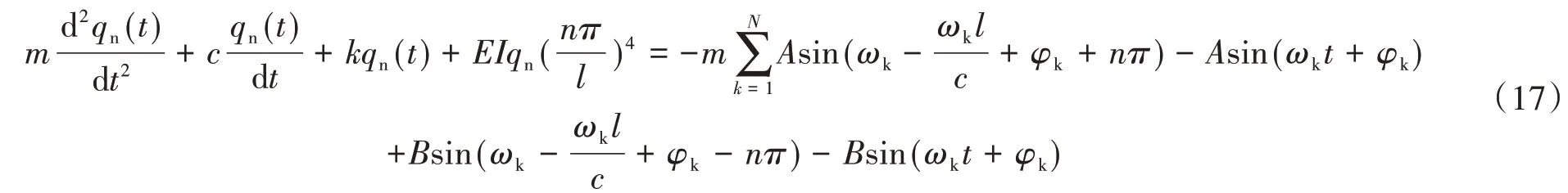
2 人工随机地震波生成

地震输入采用人工生成的随机地震波，其生成方法以平稳地震动过程的Clough-Penzien功率谱［13］为基础，引入非平稳地震动加速度过程的广义演变功率谱模型和相关参数，广义演变功率谱模型充分考虑了地震动的持续时间、地震动峰值加速度、场地土圆频率和阻尼比的时变特性，该功率谱密度函数表达式为：

式中：A(t)称为强制调制系数；c为加速度峰值对应的时刻；d为调制系数形状控制指数；S0(t)为表示地震动强度的谱参数；aˉmax为平均峰值加速度；γ为等效峰值因子。ωg(t),ξg(t)分别表示场地土自振圆频率和阻尼比；ωj(t),ξj(t)分别为过滤参数、场地参数和过滤参数均为时间的线性函数。

对于零均值非平稳地震动加速度时程a(t)，若其演变功率谱密度函数为Sa(ω,t)，则非平稳地震加速度时程可模拟为：

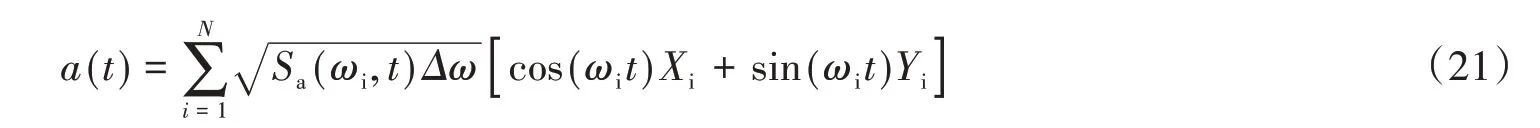
利用MATLAB编制计算程序，同时对幅值谱按照式（22）进行反复迭代修正，即可使得计算反应谱Sa(ω,ζ)向设计反应谱STa(ω,ζ)逼近，从而满足对地震动加速度时程的模拟。

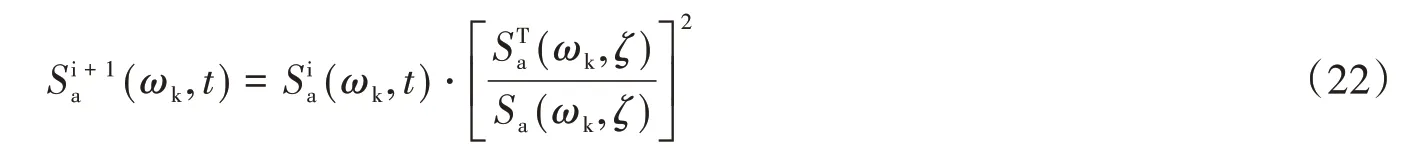
文中采用的广义演变功率谱密度函数Sa(ω,t)，可由水工设计标准反应谱确定，相关参数可根据SL 203-97《水工建筑物抗震设计规范》［14］确定。然后依据上述过程生成的人工地震波如图4所示。

图4 采用MATLAB生成的人工地震波Fig.4 Artificial seismic waves generated by MATLAB

3 计算结果分析

依据上述求解过程，采用MATLAB编制了计算程序，对算例进行了计算和分析。算例选取计算管道长度为1 000 m，沿管轴线方向200、500、800 m处分别选取3个测点，分析管道在正常、脱空和修复状况下的变形。脱空假设发生在整个管道底部（占整个管道约1/8圆环区域），沿管轴线方向贯穿整个管道底部。

人工随机地震波设计标准谱根据SL 203-97《水工建筑物抗震设计规范》［14］确定，加载方向分为纵向和横向2个方向。地震波在软土层中的传播速度一般为50～250 m/s，随土层深度的增加而增加［15］。因此文中地震波采用100、200、500 m/s这3种波速来分析。

对于振动方程中管道周围介质刚度在正常、脱空和修复3种工况下的取值，可根据之前研究成果［10］中的公式计算，具体数据可见表1，由于篇幅原因，详细求解过程就不再赘述。阻尼则采用粘滞阻尼，文中所取阻尼比取为0.05。

表1 正常、脱空和修复3种工况下计算刚度取值Table 1 Calculated stiffness values under three working conditions：normal，void and repaired

3.1 管道纵向振动计算结果分析

图5为正常、脱空和修复3种工况下，不同地震波速时，3个对应观测点处的纵向振动位移最大值的对比。由图5（b）可以看出，在相同地震波作用下，不同位置处的管道位移最大值相差不大。在脱空条件下波速500 m/s时，500 m测点处的位移最大值为21.012 mm，与200 m测点处的14.461 mm和800 m测点处的15.338 mm相比，差值分别为6.551 mm和5.674 mm，此时差值最大，其余工况差值均在1～4 mm之间。

对于同一测点，当地震波波速不同时，其纵向振动位移最大值均随波速的增加而增大。由图5（a）可以看出正常条件下测点200 m处，随着地震波波速的增大，管道位移最大值分别为2.030 mm，5.240 mm和10.139 mm，波速200 m/s和波速500 m/s的位移最大值与波速100 m/s时相比，分别增大了2.58倍和4.99倍。同样的由图5（c）可以看出，修复后测点200 m处位移最大值分别为2.548，6.733、11.634 mm，与波速100 m/s时相比分别增大了2.64倍和4.56倍。

由图5可以看出，相对于管道正常埋置条件，针对管道脱空情况下，管道的位移最大值会明显增大。如500 m测点处，与正常条件相比，波速100、200、500 m/s时脱空管道的位移最大值分别增加了3.374、5.226、9.156 mm。修复后管道的位移最大值与正常状态相比，差值较小，在500 m测点处，高聚物修复后管道的位移最大值分别为2.442，5.856、14.793 mm，与相同波速时正常条件下的位移最大值相比，误差分别为20%、21%和13%，误差较小。从上述分析也可以看出，脱空对管道有较大的影响，会使管道地震反应明显增大，经高聚物修复后，管道位移最大值会显著减小变形接近正常埋置管道的纵向位移变形，体现出高聚物注浆对管道脱空的修复效果。

图5 不同波速下管道纵向振动位移最大值Fig.5 The maximum pipe longitudinal vibration displacement under different wave speeds

图6为不同位置处管道的纵向振动位移时程曲线对比。由图6可以看出，同一地震作用下，管道在正常、脱空和修复条件下不同位置处的位移时程曲线变化趋势基本相同，同时管道各测点的反应有明显的相位特性。从图6（a）中可以看出，波速为100 m/s时，测点800 m处的位移时程曲线相对于200 m处有明显的滞后，滞后时间约等于地震波在两者之间的传播时间。波速为200 m/s时，从图6（b）中也可以看出这种滞后现象，图6（c）中由于波速较快，这种滞后现象不明显，这与文献［16］得到的结果基本一致。从图6可以看出，同一地震波波速下，不同位置管道的峰值略有不同，这是因为实际计算采用的管道长度取为定值，相较于理论假设的无限长管道，无法完全消除边界效应的影响。

图6 不同位置处管道的纵向振动位移时程曲线Fig.6 Longitudinal vibration displacement time history curves of pipeline at different positions

图7为同一位置处不同波速条件下管道的纵向振动位移时程曲线对比。从图7可以看出，管道在正常、脱空和修复情况下，同一位置处的位移时程曲线在不同波速条件下波形基本相同，位移幅值随地震波速的增大而增大。图7（a）为正常情况下200 m处的位移时程曲线，位移最大值随波速增大而增加了392%和56%，图7（b）中脱空情况下500 m处位移最大值增加了307%和111%，图7（c）为修复后800 m处的位移时程曲线，相对于100 m/s的2.752 mm和200 m/s的7.789 mm，增加了281%和34%。由此可见，考虑行波效应后，地震波波速对于管道的变形有着较大的影响。

图7 不同波速条件下管道的纵向振动位移时程曲线Fig.7 Longitudinal vibration displacement time history curves of pipeline under different wave speed conditions

图8为同一位置处正常、脱空和修复3种条件下管道的纵向振动位移时程曲线对比。从8可以看出，在不同位置和不同波速条件下，脱空管道的位移幅值相比正常情况均会明显增大，而修复后管道的位移值会恢复到正常水平。图8（a）为波速100 m/s时，800 m测点处的正常、脱空和修复位移时程曲线对比，可以看出，脱空后管道的位移值会整体增大，其最大值出现在36.7 s时为5.164 mm，此时正常情况位移为1.993 mm，修复后为2.494 mm，与正常情况相比，脱空管道位移增大了159%，修复后管道位移仅增大了25%。如图8（b）所示，当波速为200 m/s时，500 m测点处脱空管道位移最大值出现在31.1s时为6.975 mm，与正常情况（位移最大值为3.133 mm）相比，脱空管道位移增大了123%，修复后管道（位移最大值为4.352 mm）位移增大了38%。同样的图8（c）中，脱空管道位移在15.6 s时最大，为7.432 mm，此时与正常情况（位移最大值为4.045 mm）相比，脱空管道位移增大了83%，修复后管道（位移最大值为4.352 mm）位移增大了7%。由此说明底部脱空对于管道的变形会有很大的影响，脱空条件下管道整体的变形会增大，而高聚物注浆后管道的变形较正常埋置情况相比仅增加20%左右，使管道变形接近恢复到正常水平。

3.2 管道横向振动计算结果分析

图9为正常、脱空和修复3种工况下，不同地震波速时，3个测点处的横向振动位移最大值的对比。通过与图5对于可以看出，在横向振动条件下，3个测点处的位移最大值变化规律与纵向振动基本相同。在相同地震波作用下，由图9（b）所示，在修复条件下波速500 m/s时，500 m测点处的位移最大值为37.462 mm，与200 m测点处的27.61 8 mm和800 m测点处的26.423 mm相比，差值分别为9.834 mm和11.039 mm，此时差值最大，其余工况差值均在1～7 mm之间，不同位置处的管道位移最大值相差不大。对于同一测点，当地震波波速不同时，其纵向振动位移最大值均随波速的增加而增大。脱空对管道有较大的影响，会使管道位移最大值出现明显的增大，经高聚物修复后，管道的位移最大值会显著减小，与正常状况相比，误差也较小，变形接近正常使用时的变形。

图9 不同波速下管道横向振动位移最大值Fig.9 The maximum pipe lateral vibration displacement under different wave speeds

图10为不同位置处管道的横向振动位移时程曲线对比。由图10可以看出，同一地震作用下，管道在正常、脱空和修复条件下不同位置处的横向振动位移时程曲线变化趋势也基本相同，同时管道各测点的反应与纵向振动有同样的相位特性。从图10（a）中可以看出，波速为100 m/s时，这种滞后现象最明显，图10（c）中，波速为500 m/s时，不同位置处波形大致重叠，由此可见随波速的增大，滞后现象愈发不明显。

图10 不同位置处管道的横向振动位移时程曲线Fig.10 Lateral vibration displacement time history curves of pipeline at different positions

图11为同一位置处不同波速条件下管道的横向振动位移时程曲线对比。从图中可以看出，管道横向振动位移幅值随地震波速的增大而增大。图11（c）为修复后800 m处的位移时程曲线，当波速为500 m/s时，地震位移峰值最大，此时位移最大值为26.423 mm，相对于100 m/s的4.907 mm和200 m/s的11.403 mm，分别增加了438%和131%。同样的，图11（a）为正常情况下200 m处的位移时程曲线，位移最大值增加了257%和166%，图11（b）中脱空情况下500 m处位移最大值增加了717%和166%。由此可见，考虑行波效应后，地震波速对于管道的横向变形有着较大的影响。

图11 不同波速条件下管道的横向振动位移时程曲线Fig.11 Lateral vibration displacement time history curves of pipeline under different wave speed conditions

图12为同一位置处正常、脱空和修复3种条件下管道的横向振动位移时程曲线对比。从图12可以看出，在不同位置和不同波速条件下，脱空管道的位移幅值相比正常情况均会明显增大，而修复后管道的位移值会恢复到正常水平。图12（a）为波速100 m/s时，800 m测点处的正常、脱空和修复位移时程曲线对比，可以看出，脱空后管道的位移值会整体增大，其最大值出现在36.7 s时为12.541 mm，此时正常情况位移为3.993 mm，修复后为4.913 mm，与正常情况相比，脱空管道位移增大了214%，修复后管道位移增大了23%。如图12（b）所示，当波速为200 m/s时，500 m测点处脱空管道位移最大值出现在28.8 s时为42.557 mm，此时与正常情况（位移最大值为14.506 mm）相比，脱空管道位移增大了193%，修复后管道（位移最大值为11.805 mm）位移增加大了18%。同样的图12（c）中，脱空管道位移在24.8 s时最大，为72.459 mm，此时与正常情况（位移最大值为18.013 mm）相比，脱空管道位移增大了302%，修复后管道（位移最大值为24.352 mm）位移增大了35%。说明底部脱空对于管道的变形会有很大的影响，脱空条件下管道整体的变形会增大，而高聚物注浆可使管道变形基本恢复到正常水平。

图12 正常、脱空和修复3种条件下管道的横向振动位移时程曲线Fig.12 Lateral vibration displacement time history curves of pipeline under three conditions：normal，void and repaired

4 结论

文中将地下管道假定为弹性地基上的无限长均质长梁，结合提出的管-土-高聚物相互作用分析模型，忽略管道内部阻尼，建立了高聚物修复管道地震响应计算模型，同时利用振型叠加法进行了管道纵向和横向振动方程的求解，最后依据上述求解过程，输入人工随机地震波，开展了行波效应下管道高聚物修复地震响应分析。得到的结论如下：

（1）在相同地震波作用下，管道在正常、脱空和修复条件下不同位置处的位移时程曲线变化趋势基本相同，不同位置处的管道正向位移最大值和负向位移最大值相差不大。同时管道各测点的反应有明显的相位特性，距离较远测点的波形有明显的滞后现象，但随波速的增大，滞后现象愈发不明显。

（2）管道在正常、脱空和修复情况下，同一位置处的位移时程曲线在不同波速条件下波形基本相同，位移幅值随地震波波速的增大而增大。考虑行波效应后，地震波波速对于管道的变形有着较大的影响。

（3）在不同位置和不同波速条件下，脱空管道的位移幅值相比正常情况均会明显增大，而修复后管道的最大位移值基本恢复到正常水平。脱空后管道位移峰值会比正常情况下增加100%～300%，而高聚物注浆后管道的变形与正常情况相比仅增大约20%左右。可以认为底部脱空对于管道的变形会有很大的影响，而在高聚物注浆修复后可使管道变形恢复到接近正常水平。