内凹六边形蜂窝力学性能研究

曾毅翀 曹中豪

（南昌航空大学 航空制造工程学院，江西 南昌 330063）

蜂窝是典型的多孔材料，具有平面内的二维单元阵列和平面外的平行堆叠，具有周期性拓扑分布的特征。蜂窝结构比其基体材料具有更高的孔隙率和更低的质量密度，因此具有很高的比吸能、比刚度、比强度等特性。重复单胞的拓扑结构可以显著影响这些超轻材料的机械性能。因此，可以通过合理设计单胞结构使蜂窝具有前所未有的特性，如负泊松比、压缩扭转和负刚度等。这些违反直觉的性能都源于它们的微观结构特征，而不是它们的基体材料。由于其在断裂韧性、抗冲击性、散热、减振和降噪等方面的优异性能，蜂窝材料已广泛应用于建筑、汽车、船舶、航空航天、轨道交通、电子通信、生物医疗等领域[1]。

过去的几十年，针对蜂窝材料在拉伸、压缩、剪切和疲劳载荷作用下的基本力学响应已经开展了大量的研究，蜂窝结构的力学响应可分为弹性和塑性响应、静态和动态响应、面内和面外响应等。其中，负泊松比蜂窝结构是研究的热点。与传统的六边形蜂窝相比，内凹六边形蜂窝的优势在于增强了许多物理性能，例如能量吸收能力、面内断裂韧性以及在面外下形成向合曲率的能力[2]。

本文主要通过有限元数值仿真分析不同参数对内凹六边形蜂窝力学性能的影响，以获得优异的力学性能。

1 理论分析

根据Evans[3]和Masters[4]等人研究提出的六边形蜂窝结构平面内特性的解析表达式。在大多数情况下，这些表达式是基于将蜂窝胞壁符合欧拉—伯努利梁理论。

设想蜂窝在平面中加载时通过蜂窝胞壁的弯曲和拉伸以及通过在蜂窝胞壁连接处铰接而变形。因此需要考虑弯曲、拉伸、铰接三种机制结合在一起，Masters[4]等人提出了三个有关的常数Kf（弯曲常数），Ks（拉伸常数），Kh（铰接常数）。假设图1 中横斜胞壁长度分别为l 和h、厚度t 和深度b 的蜂窝的常规参数，而且组成蜂窝材料的弹性常数是已知的，包括泊松比vs、杨氏模量Es、剪切模量Gs。

图1 常规六边形蜂窝（a）和内凹六边形蜂窝（b）

通过图2、图3 来展示不同的参数（h/l、θ）对于蜂窝的泊松比（vxy、vyx）和弹性模量（Ex、Ey）的影响，进而通过调整参数可以达到改善蜂窝的性能。

在 图 2 中 已 知 定 值 b=4mm、t=2mm、s=0.3、Es=210GPa，变量h∊（2，60）,l∊（2，50）,取四个不同的角度θ（-30°、-20°、20°、30°），研究蜂窝的泊松比（vxy、vyx）和弹性模量（Ex、Ey）关于h/l 的函数关系。

由图2 可知，蜂窝的泊松比随h/l 的增加而增加，当h/l 相同时，角度θ 的绝对值越大，泊松比也越大；蜂窝的弹性模量随h/l 的增加而减小，h/l 越大，弹性模量越趋近于0，h/l 越接近于1，弹性模量越大。

图2 蜂窝的泊松比和弹性模量关于h/l 的分布曲线

在图3 中已知定值b=4mm、h=30mm、t=2mm、s=0.3、Es=210GPa，变量θ∊（-60°，60°）, 取三个不同的l（10、20、30），研究蜂窝的泊松比（vxy、vyx）和弹性模量（Ex、Ey）关于θ 的函数关系。

图3 蜂窝的泊松比和弹性模量关于θ 的分布曲线

由图3 可知，蜂窝的泊松比vxy和弹性模量Ex都随θ 绝对值的增加而增加；泊松比vyx随θ 的增加而先增加后减小，趋近于0；弹性模量Ey关于θ=0°类似于正态分布，角度越接近0°，弹性模量越大。

A阴性空白对照——25 μl去离子水+25 μl底物（37 ℃孵育 10 min）+50 μl去离子水（37 ℃下孵育60 min）+100 μl醋酸-醋酸钠缓冲溶液。

2 模型仿真与分析

根据上面的理论分析，可以选取合适的蜂窝几何参数进行参数化建模、有限元分析，进而完成蜂窝结构力学性能分析。

2.1 几何参数对单胞结构的影响

2.1.1 长度h 对单胞结构的影响

以长度h 为变量，其余几何参数为不变量，研究长度h 对单胞结构力学性能的影响。

b=6mm,t=3mm,l=10mm,θ=60°,h=20,30,40,50mm。

由图4 图5 可知，随着h 增加，泊松比vxy的绝对值增加，弹性模量Ex增加，泊松比vyx的绝对值减少，弹性模量Ey减少。在合理误差范围内，理论值和仿真值趋于吻合。

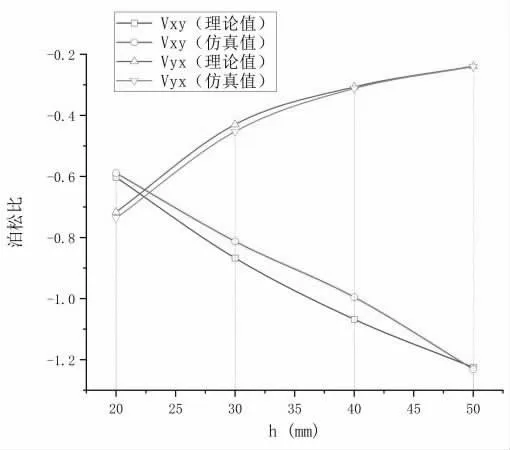
图4 泊松比随h 的变化图

图5 弹性模量随h 的变化图

2.1.2 长度l 对单胞结构的影响

以长度l 为变量，其余几何参数为不变量，研究长度l 对单胞结构力学性能的影响。b=6mm,t=3mm,h=50mm,θ=60°,l=10,20,30, 40mm。

图6 泊松比随l 的变化图

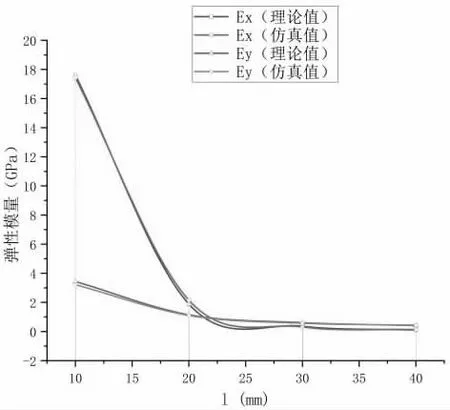
图7 弹性模量随l 的变化图

2.1.3 角度θ 对单胞结构的影响

以角度θ 为变量，其余几何参数为不变量，研究角度θ 对单胞结构力学性能的影响。

b=6mm,t=3mm,h=50mm,l=20mm,θ=50°,60°,70°,80°。

由图8 图9 可知，随着θ 增加，泊松比vxy的绝对值减少，弹性模量Ex减少，泊松比vyx的绝对值增加，弹性模量Ey增加。在合理误差范围内，理论值和仿真值趋于吻合。

图8 泊松比随的变化图

图9 弹性模量随的变化

2.2 蜂窝结构的有限元分析

为了有限元仿真结果可以与实验结果对比，故采用ZIED K[5]等人所提供的尺寸参数，b=8mm、t=2.86mm、h=42mm、l=42mm、θ=67°、vs=0.3、Es=210GPa。

在有限元软件ANSYS APDL 中建立参数化模型，采用梁单元Beam188,并进行静力学仿真，提取结构的位移变化量，并计算出泊松比和弹性模量。仿真效果见图10，其力学性能结果见表1 所示。

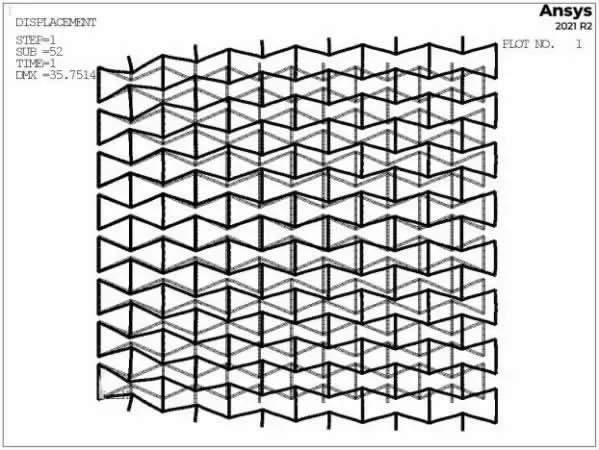
图10 仿真变形效果图

表1 内凹六边形蜂窝力学性能结果

由表1 可知，本论文的有限元分析结果比论文[5]中的实验结果略高一些，在合理误差范围内比较吻合，验证了理论公式的正确性。产生误差的原因是有限元分析时，采用的梁单元在蜂窝的横胞壁和斜胞壁交接处有重合现象，导致结果偏大，此外，在有限元后处理中的取值存在一定的误差，也会导致结果偏大。

3 结论

通过理论值和有限元仿真值得对比分析，可以看出X 方向的等效弹性模量Ex受长度h、l 的影响较大，Y 方向的等效弹性模量Ey受长度h、角度θ 的影响较大，泊松比受这三种的几何参数的影响都较大。这些规律可为负泊松比超材料设计提供一定的参考依据。