3D打印TPMS多孔材料力学性能数值仿真
李心远,宋卫东,陈 键
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
多孔材料以其优异的吸能效率、热传导性能等物理特性吸引了大量的科学家对其进行深入的研究[1-4]。多孔材料可分为天然多孔材料和人造多孔材料,而人造多孔材料通常又可分为蜂窝材料和泡沫材料。其中,泡沫多孔材料可以分为闭孔型和开孔型两种;按材质的不同还可以分为多孔金属、多孔陶瓷、多孔塑料等。多孔金属材料不仅保留有比强度高、热导率低等优势,还具有优良的机械加工性能、导电性、延展性等特点。对于传统多孔材料,通常采用3D打印技术加工成型但效率较低,研究人员为此提出了“三周期极小化曲面”(TPMS)拓扑法[5]。通过这种方法拓扑而成的结构拥有许多优势,如良好的热导电性,完美的孔隙互连,高表面积与体积比,孔隙结构易控性,高强度和刚度等。
国外的研究者利用TPMS原理在多孔材料结构设计方面进行了一系列的研究,并取得了不少的成果。KAPFER et al[6]利用三周期极小化曲面法设计了两种支架结构,并证实了在相同的相对体积下,片状结构比网格状结构拥有更大的体积模量和杨氏模量。YOO et al[5,7]则对TPMS拓扑结构在组织结构方面进行应用研究,发现将距离场的概念与TPMS原理相结合,可以更便捷地设计出微观结构更复杂、外表面质量更高的单胞模型,其应力应变曲线拥有更长的平台段,弹性模量和峰值应力都普遍高于其他结构,表明其在承载及吸能等方面有更好的能力。KADKHODAPOUR et al[8]为了研究TPMS多孔结构的内部构型对变形模式的影响,设计了两种不同相对体积的结构进行了实验和数值仿真,结果证实不均匀的质量分布会导致应力集中现象的出现,进而导致与传统多孔材料不同的应力应变曲线。ORAIB et al[9-11]设计了多重TPMS拓扑结构,通过准静态压缩实验对其力学响应进行了研究,结果表明壳型TPMS结构的变形模式以拉伸为主导,骨骼状的TPMS结构则为弯曲主导型,并且壳-菱型复合结构的刚度与其相对体积大小的相关性很小。综上所述,基于TPMS法生成的壳型结构表现出更优越的力学性能,在相对体积较小的情况下,几何结构对材料的力学性能有较大的影响。
本文采用LS-DYNA有限元软件,探究了在不同冲击速度下,不同相对体积的螺旋二十四面体单胞及2个×2个×2个八胞体模型的承载力及能量吸收能力,为该结构的吸能性能提供理论支撑。
1 数值模拟
1.1 实体模型生成
三周期极小化曲面螺旋二十四面体如图1所示,该拓扑结构的数学表达式为:
sinxcosy+sinycosz+sinzcosx=c.

图1 螺旋二十四面体结构模型[11] Fig.1 Gyroid TPMS architecture[11]
利用Wolfram Mathematica软件,以TPMS的基本公式为基础编写程序,并生成“.stl”格式的模型文件。随后将文件导入前处理软件Hypermesh中,单胞模型的大小通过比例放大将外边框边长设置为10 mm×10 mm×10 mm,八胞体模型(2个×2个×2个)边长为20 mm×20 mm×20 mm.再利用其2D面板下携带的Shrink Wrap功能,对导入的单胞结构进行自动的网格划分。图2所示为相对体积为10%,30%,50%的单胞以及相对体积为10%,30%,50%的八胞体的有限元模型。

图2 不同相对体积下单胞结构与八胞体的有限元模型 Fig.2 Finite element model of unit cell and eight cells with different relative volume percentages
1.2 计算参数与接触设置
与铝合金相比,钛合金具有更高的弹性模量和断裂强度,采用钛合金作为多孔结构的基体材料可以更大地提升结构的抗压缩承载能力以及能量吸收能力。材料模型选用传统的PLASTIC_KINEMATIC模型,部分相关参数如表1所示。
利用ANSYS/LS-DYNA对上述模型进行了数值仿真研究,探究不同相对密度单胞及不同压缩速率对结构承载及吸能性能的影响,计算模型如图3所示。在K文件中通过RIGIDWALL_GEOMETRIC_FLAT_MOTION定义上刚性墙施加单轴压缩载荷,上刚性墙的加载速度v=5,30,50 m/s,对单胞进行恒速压缩,通过ε=v/h(h为压缩方向上单胞的高度)可得出单胞的整体应变率分别为500/s,3 000/s和5 000/s.为保证整体应变率对应相同,对八胞体分别采用10,60,100 m/s的速度进行压缩。利用RIGIDWALL_GEOMETRIC_FLAT定义下刚性墙且保持静止。多孔材料接触参数采用*CONTACT_SURFACE_TO_SURFACE.
2 计算结果与讨论
2.1 力-位移曲线
图4所示为相对体积分别为10%,30%,50%单胞和八胞体受到不同恒速压缩的力-位移曲线。

表1 单元材料模型Table 1 Material models for elements

图3 完整的计算模型 Fig.3 Entire simulation model
不同相对体积单胞及八胞体在等速度下的力-位移曲线如图5所示。从图中可以看出,不同相对体积多孔结构的峰值力的明显不同,相对体积较大的结构峰值力更高,平台段更为平缓。
为了对比相对体积和冲击速度对结构承载能力的影响,引入坍塌力Fc与平台力Fp来衡量结构的力学性能,其中坍塌力表示曲线弹性段的初始峰值力。由于不同结构相对体积即实体材料所占体积并不相同,将坍塌力和平台力比体积化,分别得出比坍塌力Fcv和比平台力Fpv,计算公式如下所示:

图4 等相对体积不同速度下单胞与八胞体模型的力-位移曲线 Fig.4 Force-distance curve of structure with different velocity and uniform of relative volume percentages

图5 等速度、不同相对体积下的单胞与八胞体模型的力-位移曲线 Fig.5 Force-distance curve of structure with different and uniform velocity of unit cell and eight cells
(1)
(2)
(3)



图单胞的应力-应变、变形效率-应变曲线 Fig.6 Stress/deformation efficiency-strain curve
密实段位移可根据图中所得的密实应变通过公式hd=h0×εd求得,其中h0为试件在加载方向的高度。模拟所得力-位移曲线中各种工况下结构的坍塌力和平台力大小如表2所示。

表2 各种工况条件下结构的坍塌力Fc和平台力FpTable 2 Collapse force Fc and plateau force Fp of cells in different conditions
由表2中数据可以看出,随着相对体积的增大,单胞的坍塌力越大,代表其承载能力越强。这是由于相对体积越大,单胞中实体材料占比越多,结构中实体部分表面厚度越厚,导致其承载能力增强。在相同的相对体积下,八胞体的坍塌力明显高于单胞的坍塌力,原因如下:八胞体相较于单胞,实体材料相互连接行程更长,导致其在受到压力时结构具有更长的吸能行程,可以将压力快速地均匀分布在结构的实体材料上,减小局部所承载的压力值,因此八胞体拥有更为出色的承载能力。
通过对比相同相对体积单胞的计算结果可以发现,高冲击速率下结构的坍塌力更高。借鉴应力增强因子aDIF的概念(动态坍塌强度与静态坍塌强度的比值),由于3种单胞尺寸均为10 mm×10 mm×10 mm,故此处可用坍塌力代替坍塌强度。5 000/s应变率相比于500/s应变率,相对体积为10%,30%,50%单胞的aDIF分别为1.52,1.28,1.24,说明该结构表现出一定的应变率敏感性,并且相对体积越小,应变率敏感性越明显。
相对体积与冲击速率对平台力与坍塌力的影响基本一致。另外可以看出,对于相对体积为30%和50%的单胞,其平台力大于坍塌力;这是由于力-位移曲线中平台段较初始峰值力没有大幅下降,并且出现了较为明显的平台硬化现象。
表3所示为各种工况下模型结构的比坍塌力和比平台力对比图。从计算结果可以看出,对于单胞结构,比坍塌力和比平台力均随着相对体积的增加和冲击速率的提高有较为明显的提升。在5 m/s的冲击速率下,相对体积30%的单胞的比坍塌力和比平台力相较于相对体积10%的单胞分别提高1.56和1.11,而相对体积50%的单胞相较于相对体积30%的单胞提升仅有0.34和0.43;同时,在50 m/s冲击速率下,相对体积30%的单胞的比坍塌力和比平台力相较于相对体积10%的单胞分别提高1.33和0.81,而相对体积50%的单胞相较于相对体积30%的单胞提升仅有0.37和0.40.这些数据说明,虽然相对体积越大,单胞的承载能力越强,但当相对体积越大,其对单胞承载能力的提升越不明显,因此在实际应用中,应综合考虑材料成本与承载要求需要,合理选择单胞的相对体积,不可盲目增大相对体积以达到更强的承载效果。此外对于八胞体,其比平台力及比坍塌力均小于单胞,但是在较大相对体积下的比坍塌力及比平台力均有一定的上升。
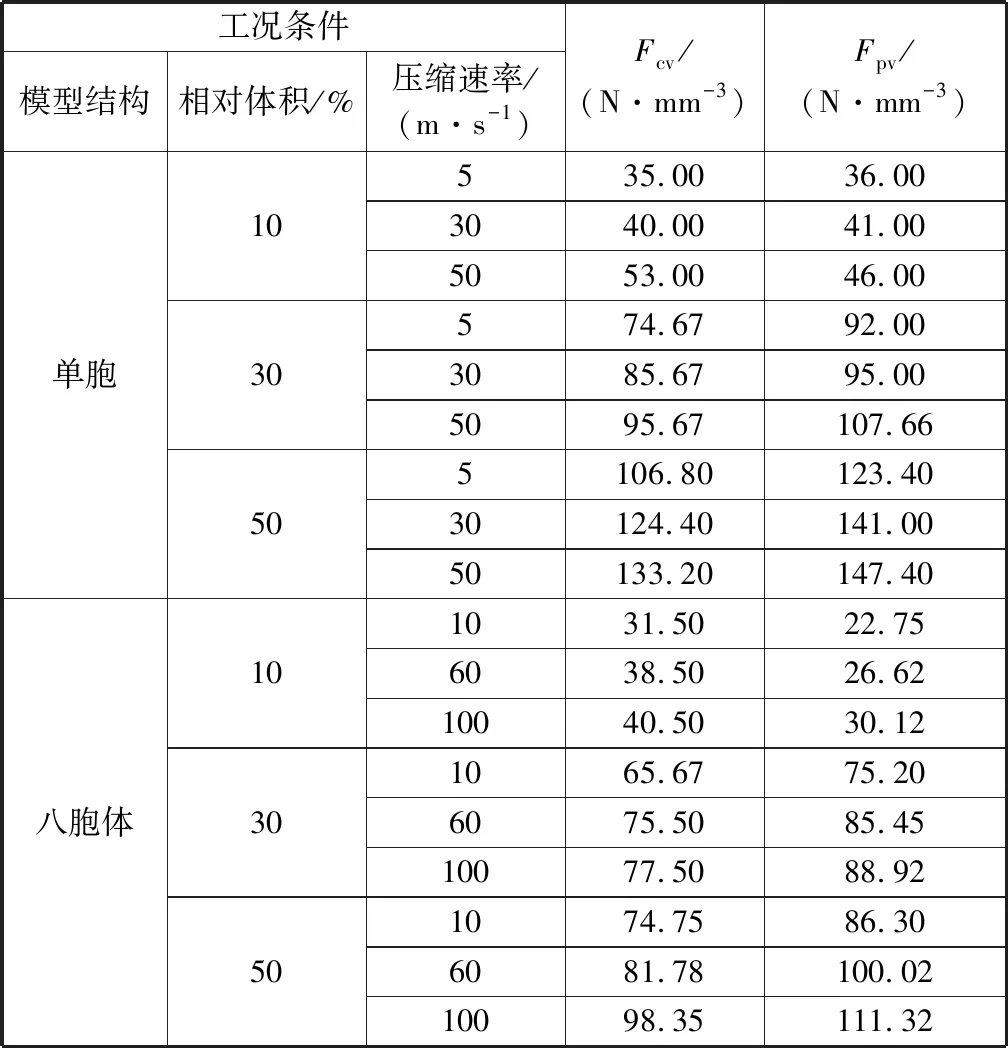
表3 各工况条件下模型结构的比坍塌力Fcv和比平台力FpvTable 3 Specific collapse force Fcv and specific plateau force Fpv with different conditions
2.2 能量吸收
体积比吸能是指单位体积材料吸收的能量大小,可使用下述公式进行计算:
式中:E为吸收的总能量,J;hd为力-位移曲线中密实段起点处对应的行程;F为冲击力;Vs为实体部分体积。通过计算,上述工况下各结构的体积比吸能如表4所示。

表4 各工况条件下模型结构的体积比吸能wSEATable 4 Volume specific energy absorption wSEA with different conditions

2.3 应力分布
图7为相对体积10%的单胞受到5 m/s时冲击的应力云图的俯视图(图9(a),9(c),9(e))与侧视图(图9(b),9(d),9(e).从图中可以看出,在压缩过程中,该结构通过张开其顶部与底部的曲面将应力均匀分布于实体部分。从机械的角度分析,螺旋型结构由于其本身的特性拥有极为光滑的表面,胞体之间由连续且光滑的表面过渡和连接。这导致其不同于传统的支撑型结构,后者由于模型边缘和棱角的存在会导致应力集中现象的产生,容易在局部发生大变形以致结构过早失效。螺旋二十四面体单胞在整个冲击压缩的过程中,其边缘曲面结构不对称的特点容易导致结构发生弯曲变形,导致在压缩过程中整体结构有扭转的趋势,通过整体的压缩以及结构的扭转将能量吸收。并且由于该结构由曲面构成,在固定的单胞体积内曲面增加了结构实体部分应力分布的面积,也使得压力可以较为均匀地分布于结构表面,使得局部应力最小。因此,螺旋体相比于其它结构拥有更好的吸能与承载性能。

图单胞的应力云图 Fig.7 Stress nephogram of m/s unit cell
由图8所示的八胞体受到冲击载荷下应力分布云图可以看出,连续且光滑的结构设计可以快速地将应力均匀分布在结构表面。在受到100 m/s高速冲击载荷下,靠近冲击端与承载端的单胞首先发生屈曲;当两端单胞孔隙压缩到一定程度时,曲面相互接触,结构内部相邻两层单胞开始发生明显变形,曲面屈曲吸能。从整体上看,当螺旋二十四面体单胞的拓扑结构受到100 m/s高速动态压缩载荷后,连续曲面可将应力迅速分布到结构内部,整体发生从两端向中心的逐层破坏,结构内部孔隙充分发挥减震抗冲击性能,曲面受力均匀,具有良好的吸能承载能力。

图八胞体的应力云图侧视图 Fig.8 Stress nephogram side view of v=100 m/s eight cells
3 结论
轻质多孔材料由于其自身的高比强度、高吸能效率等特性具有广泛的工程应用前景。本文通过数值仿真计算了不同相对体积下,多孔结构在低、中、高速压缩载荷下的力学响应及吸能特性,研究了冲击速度、相对体积以及胞体数量对结构在静动态加载下变形机理和吸能效率等方面的影响。主要结论归纳如下:
1) 随着相对体积的增大,单胞的坍塌力和平台力明显增大;但相对体积越大,其对单胞承载能力的提升越不明显。相对体积为30%和50%的单胞力-位移曲线平台段硬化现象明显,平台力大于坍塌力。
2) 该结构具有一定的应变率敏感性,高冲击速率下结构的坍塌力和平台力明显提高,比坍塌力和比平台力均随着冲击速率的提高有较为明显的提升。
3) 相对体积和冲击速率对单胞及其八胞体的体积比吸能有明显的影响。对于相同的冲击速度,单胞的体积比吸能均随着相对体积的增大有较为明显的上升,对于相同的相对体积,结构所受冲击速率越大,其吸能总量及吸能效率越大。
4) 通过TPMS法设计的多孔结构曲面能够将应力均匀分布到实体材料上,使其在整个冲击压缩过程中没有明显的应力集中现象发生。受到高速冲击时,靠近冲击端和承载端的曲面通过弯曲变形将能量吸收,结构内部孔隙同样起到优秀的缓冲吸能的作用。

