核汽轮机DEH 系统动态特性仿真及扰动因素研究
林 安,陈国兵,张 磊
(海军工程大学动力工程学院,湖北武汉 430032)
核汽轮机是许多海洋平台、大型船舶的重要推进装置,随着核动力汽轮发电机组的容量不断增大,对机组的鲁棒性和负荷适应性要求越来越高[1-4],核汽轮机调节控制系统已由机械液压调节系统、模拟式电液调节系统发展到如今广泛应用的DEH(Digital Electric Hydraulic)系统。DEH 系统是复杂的非线性系统,非线性因素、外界扰动和结构参数的变化都会严重影响系统的动态性能[5-7],很多学者在此方面开展了大量研究[8-13]。当前的汽轮机及其DEH 系统模型难以精确地反映外界扰动、DEH 结构参数变化对系统的动态特性影响规律。因此,该文以核汽轮机DEH 系统为对象,开展汽轮机与调节系统的耦合建模仿真研究,并实现扰动工况下汽轮机动态运行特性及影响因素分析,为核汽轮机及其DEH 系统运行优化提供技术支撑。
1 核汽轮机DEH系统模块化建模
核汽轮机DEH 系统框图如图1 所示,DEH 系统主要由转速控制器、伺服放大器、电液转换器、滑阀油动机与汽轮机转子等组成。转速给定值作为给定信号,转子输出转速作为反馈信号,以给定信号与反馈信号的偏差作为PID 控制器的输入信号,经伺服放大器输出为电流信号,油动机输出的阀位信号作为反馈信号,以电流信号与阀位反馈信号的偏差作为电液转换器的输入信号,输出油动机滑阀位移信号,通过调节油动机阀位调整高压主汽阀的阀门开度,从而改变蒸汽进汽量来调节转子转速。当测速器输出的转速反馈信号与给定信号相同时,偏差信号输出为零,此时转子转速达到目标转速。
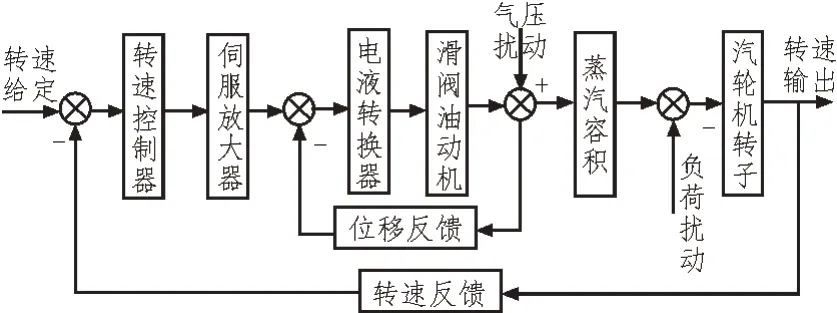
图1 DEH系统框图
将图1 中DEH 系统进行模块化建模,建模考虑以下条件:①针对小偏差进行线性化处理;②运动部件的质量不计;③液态摩擦力不计。建立各主要环节的传递函数数学模型。

根据各环节的数学模型、传递关系和反馈理论,耦合后得到DEH 系统数学模型。
2 PID参数整定
以某型单缸汽轮发电机组为参考对象,该汽轮机组DEH 系统相关参数如表1 所示。利用劳斯稳定性判据,得到稳定响应下的PID 控制器参数的取值范围。结合Matlab∕Simulink 的临界比例度法和衰减曲线法完成PID 参数整定。

表1 系统参数值
2.1 利用劳斯判据,得到参数范围
调节系统的闭环传递函数为:

根据劳斯判据,系统稳定的充分必要条件是:特征方程的全部系数都是正数,并且劳斯数表的第一列元素都是正数[14]。得出参数的范围如下:
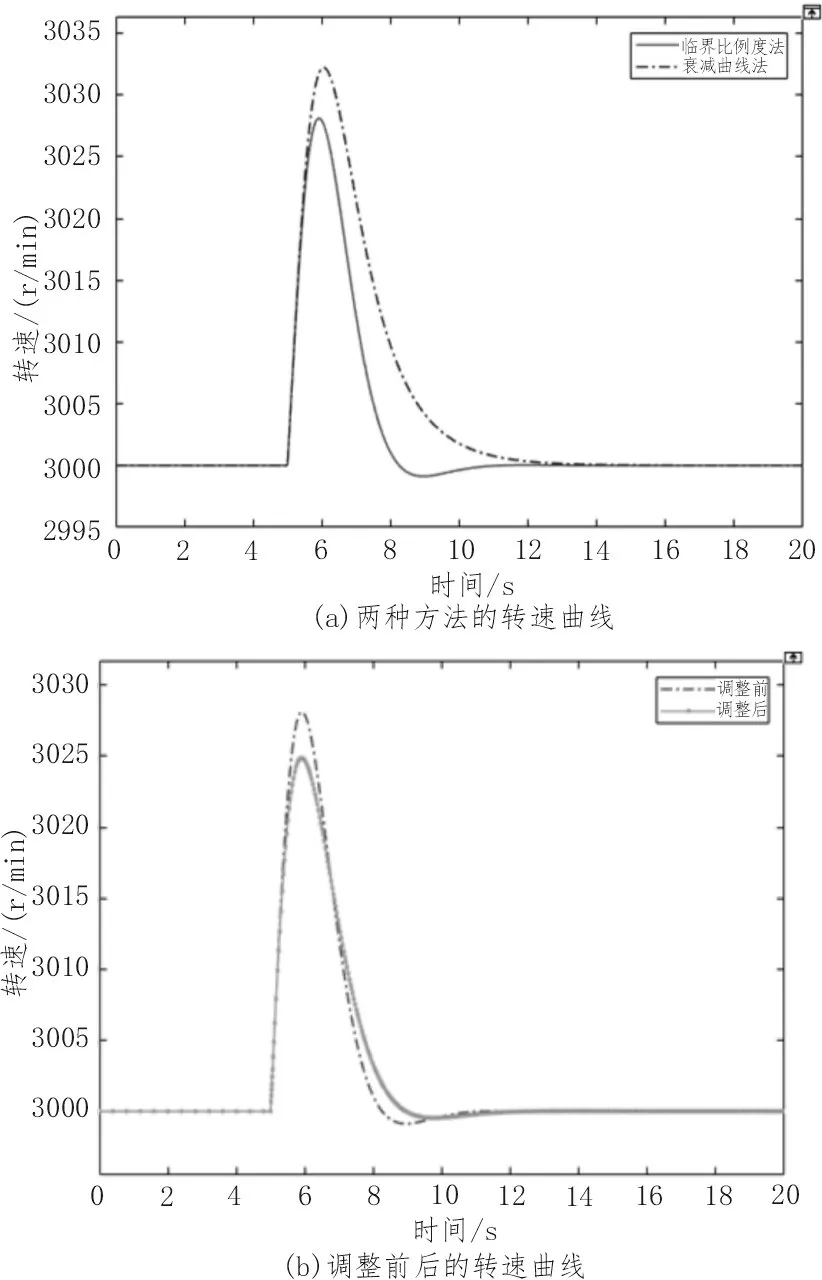
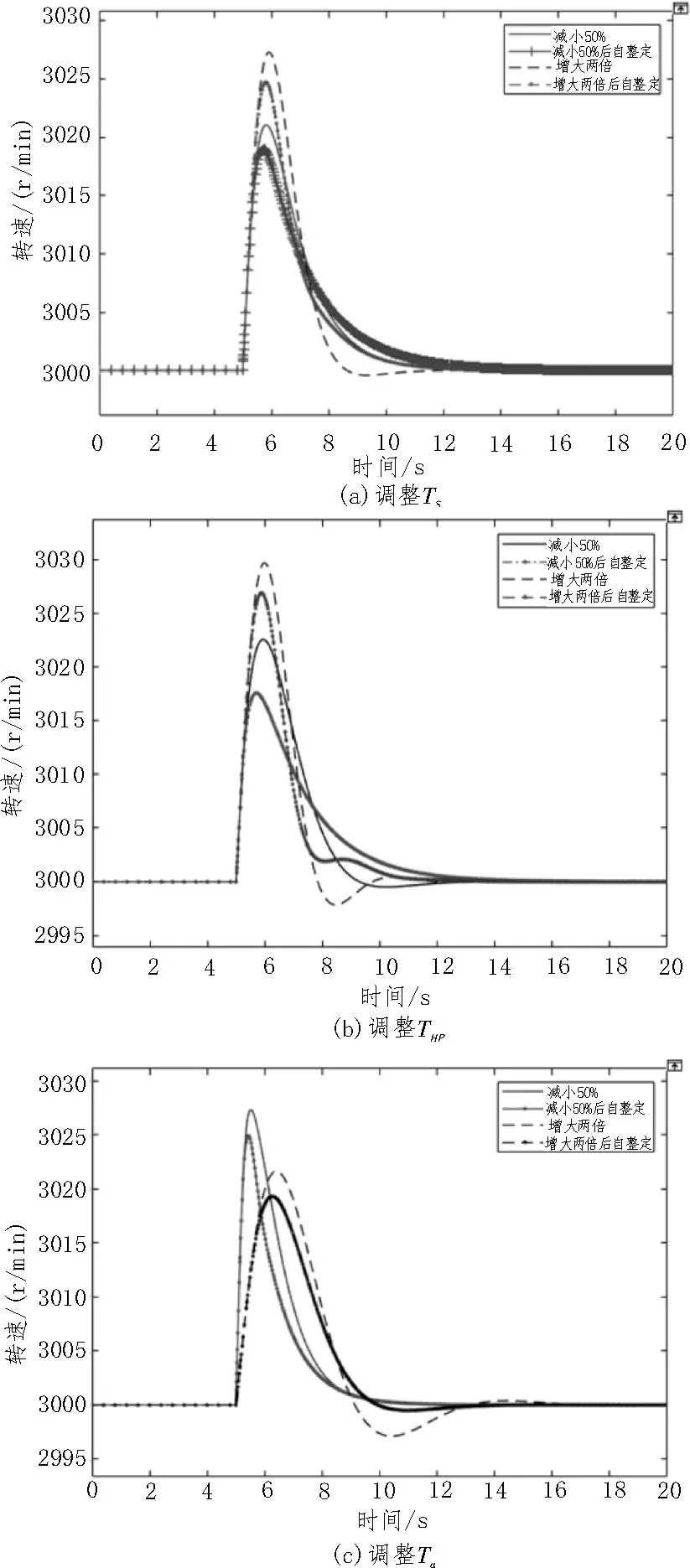
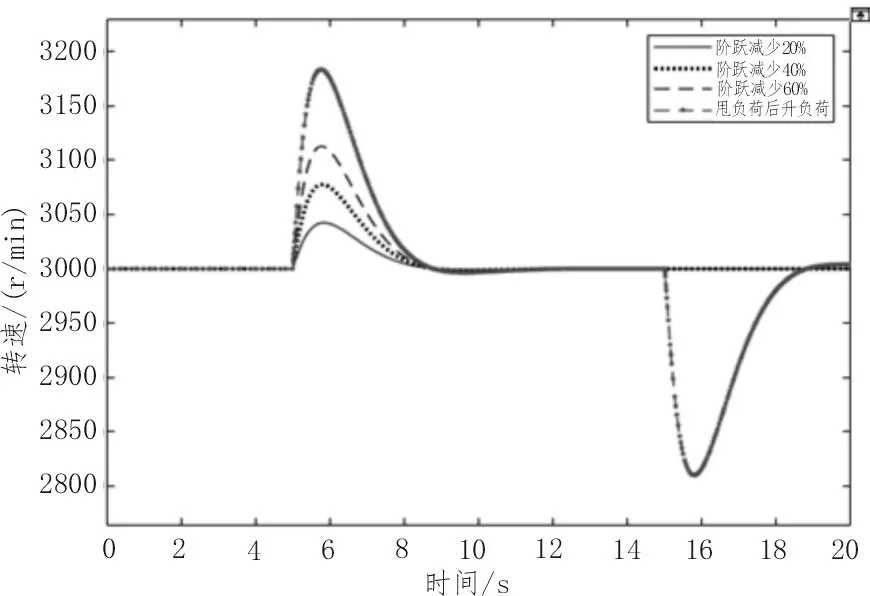
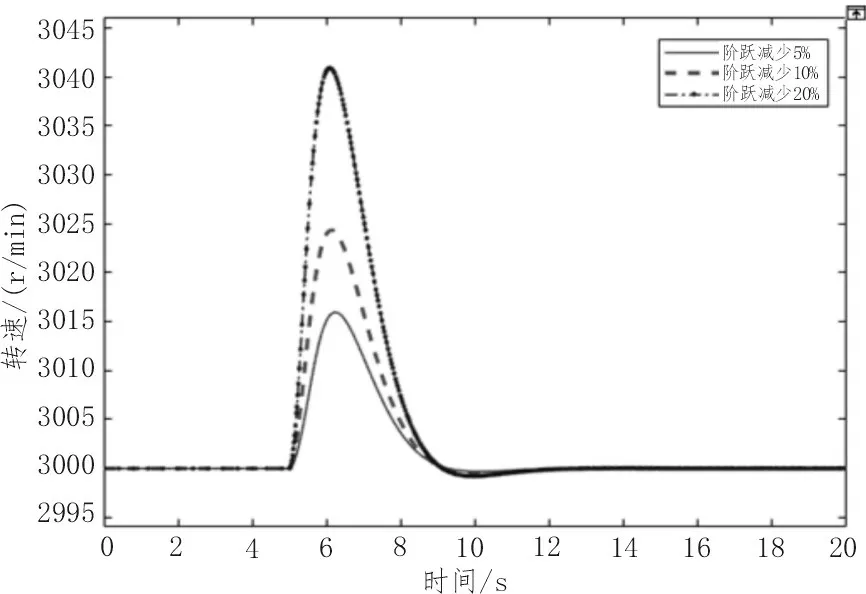
0 不考虑PID 控制器的函数,将表1 中参数代入公式(1),可得到系统的开环传递函数为: 临界比例度法获取系统的等幅振荡曲线,从而求得临界增益Ku和临界振荡周期Tu [15]。在Simulink 环境实现步骤如下:设置PID 参数的名称及配置仿真参数;根据上述求得Kp的范围,完成PID 参数的初始化,采取折半取中的方法寻找临界增益,直至出现等幅振荡,从等幅振荡曲线中近似地测量出临界振荡周期。依照此方法可得Ku=1.85、Tu=1.618,根据临界比例度法经验公式Kp=0.6Ku、Ti=0.5Tu、Td=0.125Tu,得到参数的取值如下: 衰减曲线法按照“先P 后I 再D”的调整步骤,设置比例放大系数,积分时间设为足够大,微分时间设为零[16]。不断调整参数至调节系统稳定,然后逐步减小比例度,观察调节过程的曲线波动情况,直到出现4∶1 的衰减过程后停止,记录δs和Ts。依照此方法得到δs=1.244、Ts=1.597。根据衰减曲线法的经验公式Kp=0.8δs、Ti=0.3Ts、Td=0.1Ts,求得参数的取值如下: 以该文建立的模块化数学模型为基础,采用Simulink 中的死区和限幅模块来代替系统中死区、限幅和摩擦等非线性因素的影响,构建DEH 系统的动态仿真模型,开展两组不同PID 参数的甩负荷仿真研究。其中汽轮机额定转速为3 000 r∕min,仿真时间为20 s。 将表1 参数代入DEH 系统数学模型中,将临界比例度法和衰减曲线法得到的PID 参数分别代入PID 控制器中进行动态仿真,分析汽轮机突然甩负荷时的动态响应特性,如图2 所示。 由图2(a)可得,结合Simulink 的临界比例度法与衰减曲线法相比,甩负荷后转速动态超调相对较小,约为6.7%;转速调整时间更小,约为7 s;系统稳定性更好,整定效果更显著,整定精度高。因此该文对PID 参数的自整定采用结合Simulink 的临界比例度法。 根据经验对PID 控制器参数再进行微调整,可得到PID 控制器参数如下: 将新参数代入PID 控制器中,按照上述步骤可得如图2(b)所示的微调整前后汽轮机甩负荷转速曲线。由图2(b)可得,微调后动态超调略有下降,约为5.8%;转速响应迅速,调整时间略小于7 s,比纯液压调节的动态超调和调整时间都小,该系统动态响应良好,稳定性较高。 图2 甩负荷后转速输出曲线 影响调节系统动态特性的主要因素有油动机时间常数、中间容积时间常数和转子时间常数。为了研究这些参数变化对系统动态响应的影响规律,DEH 系统方案保持不变,将Ts、THP、Ta减小50%或增大2 倍,同时利用上述结合Simulink 的临界比例度法和经验法完成PID 参数的自整定,仿真得到参数调整后的转速输出曲线如图3 所示。 由图3 可得,当DEH 系统结构参数变化时,应用PID 参数自整定的方法,可以分别求取各参数变化后所对应的PID 参数值,这些参数对于系统的整定效果较原有参数更显著,有利于减少系统的动态超调和调整时间,减小系统的振荡,增强系统的稳定性和响应速度。此外,系统的动态超调和调整时间与Ts和THP的大小成正比,Ts和THP越小,动态超调与调整时间越小,系统稳定性越好;Ta越小,调整时间相对略短;但Ta越大,动态超调越小,振荡幅度相对更小,系统稳定性增强。总的来说,Ta的变化对动态特性的影响较Ts和THP更显著,汽轮机转子在维持系统稳定性方面至关重要。在实际运行中,为了防止Ts和THP过大、Ta减小而导致系统动态响应较差,可以通过减小活塞面积、增加油口宽度、增大油压来减少Ts;减少蒸汽室容积,减小THP;增加转子的质量和半径,增加额定转速来增大Ta等改善系统的动态响应特性,增强系统的稳定性。 图3 各参数调整后的转速输出曲线 实际运行中,机组经常会受到扰动的影响,主要为系统的内扰蒸汽压力扰动和外扰负荷的变化。了解扰动对汽轮机运行影响的规律,有助于实现汽轮机的优化运行。 核汽轮机长期以额定或接近额定功率运行,当机组负荷突然减少时,汽轮机转速会快速上升,造成设备振动加剧,当振动过大时易引起共振导致设备损坏。将负荷扰动模块的参数Final value 分别设置为0.2、0.4、0.6,压力扰动模块的参数Final value 设置为0,其余模块参数不变,用以表示负荷阶跃减少20%、40%、60%。同理,其他不变,将负荷扰动模块的参数Phase delay 设置为5,Period 设置为20,Pulse Width 设置为50,表示汽轮机5 s 后甩负荷,15 s 后升负荷,仿真后得到负荷阶跃变化的转速输出曲线如图4 所示。 图4 负荷阶跃变化的转速输出曲线 由图4 可得,当负荷阶跃减小时,进汽阀门开度将减小,此时汽轮机容积中残余大量蒸汽,导致汽轮机内部气压增大,转子转速迅速增加,且负荷阶跃减少越多,转速上升幅度越大,甩负荷转速上升最快,动态响应约为6%;同理可得,当负荷快速上升时,转速迅速下降,且不论升减负荷转速都能在7 s 内稳定下来;总的来说,系统抗扰动能力较强,稳定性好。在实际运行时,当汽轮机减负荷时,为了减小对设备造成的危害,提升运行的经济性和安全性,应该减小调节阀门开度,这将对调节阀门的气密性要求较高,需要装备精度较高的阀门,使汽轮机的蒸汽减少量跟上负荷减少的阶跃量,以此抵消负荷阶跃减少所造成的机组运行时的不利影响。 汽轮机在运行过程中当汽压降低到一定程度时,会导致叶片变形、喷嘴堵塞和汽轮机功率达不到额定功率等危害。将压力扰动模块的参数Final value 设置为-0.05、-0.1、-0.2,负荷扰动模块的参数Final value 设置为0,其余模块参数不变,用来表示蒸汽压力阶跃减少5%、10%、20%,仿真后得到如汽压扰动变化的转速输出曲线如图5 所示。 由图5 可得,当蒸汽压力突然降低时,汽轮机负载会随之减小,转速由于负载减小会快速上升,且汽压扰动越小,转速上升越快,动态超调越大,但转速都在7 s 内稳定为额定转速,总的来说系统抗扰动能力较强,稳定性好。在实际运行时,导致蒸汽压力降低的因素主要有蒸发室来汽压力降低,主蒸汽管道泄漏和自动主汽门门芯脱落等,可以通过增加蒸发器燃料供应、增大调节汽阀开度和降低汽轮机的负荷等方式来增加蒸汽的流量,避免蒸汽压力过低而对设备造成的损害,保证汽轮机平稳安全运行。 图5 汽压扰动变化的转速输出曲线 1)建立的核汽轮机DEH 系统模块化数学仿真模型添加了限幅和死区等非线性模块和负荷与汽压扰动模块,仿真后动态超调较小,响应速度较快,稳定性能较好,精度较高;结合Simulink 的临界比例度法较衰减曲线法具有更加直观、易于实现、响应精度更高和控制效果更好的优点。 2)Ta的变化对动态特性的影响较Ts和THP更显著,减小Ts和THP、增大Ta可以改善系统的动态响应特性,增强系统的稳定性;扰动的变化对系统的转速调整时间几乎无影响,但系统的动态超调会随着扰动的增大而变大,稳定性会变差。这些研究为核汽轮机DEH 系统参数优化和运行优化提供了参考依据。2.2 临界比例度法
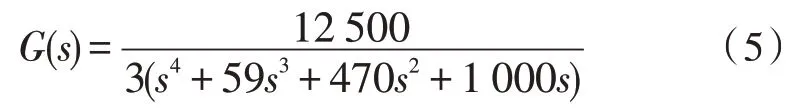
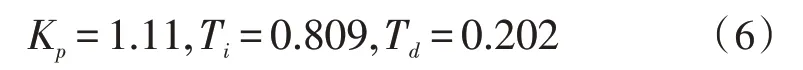
2.3 衰减曲线法
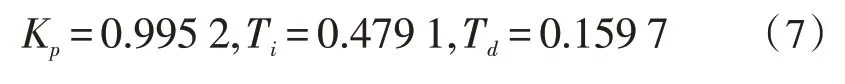
3 DEH系统动态仿真分析
3.1 两组PID参数对系统动态特性的影响
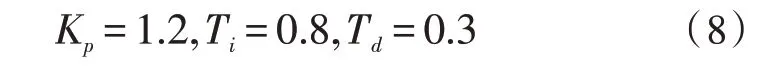
3.2 DEH系统参数变化动态特性分析
3.3 外界扰动特性分析
4 结论

