城市轨道交通车辆网络节点重要性分配优化算法研究

李宏菱

（西安铁路职业技术学院，陕西西安 710026）

城市轨道交通系统是一个开放的动态复杂网 络，其复杂的拓扑结构也是轨道交通系统运行的基础[1-2]。迄今为止，复杂网络理论已广泛应用于诸多领域，包括公共交通领域，如铁路、公交、轨道交通、城市道路等[3-4]。研究表明，复杂网络是分析城市轨道交通网络拓扑性质的有效工具。其基本思想是首先对未加权或已加权的轨道交通网络进行建模，然后通过不同的拓扑指标或一些已提出的指标来探索网络的复杂性，如程度中心度(DC)、中间中心度(BC)、接近中心度(CC)、特征向量中心度(EC)、平均最短路径长度(APL)、页面排名(PR)、K 系数中心度(KS)等[5-8]。对于城市轨道交通网络发展中的不同站点，节点重要性演化受拓扑结构和客流变化的影响也不同，因此需要结合实际情况进行具体分析[9-12]。

该文在轨道交通网络演化过程中，建立了6 个未加权和已加权的复杂网络模型。在此基础上，提出了变异系数法和理想解法相结合的多属性决策方法，同时结合实例对于不同的站点，定量和定性地讨论了节点重要度变化因素之间的相关性，并且深入地分析了演化机制。

1 节点重要性评估

在复杂网络中，识别最具影响力的节点是理解和控制传播过程中的重点[13-14]，因此城市轨道交通网络迫切需要节点重要性评估。算法所得出的结果可用于评估车站存在的风险以及未来的预测和预警[15]，从而有利于提高网络的弹性和安全性。目前，大多数关于节点重要性评估的研究均是基于对复杂网络拓扑指标的分析，代表性的研究成果如表1 所示。

表1 中研究网络节点的重要性基本上是从连通性重要性和抗毁性重要性两个角度来评估，分别基于中心性度量和级联失效来获得，对节点重要性演化的研究仍不够深入。单一属性测量方法存在较多缺点，大多数研究广泛使用的索引重要度是DC、BC、CC和EC。局部指标较为简单，如DC可利用有限的信息，但不能有效地确定重要节点。全局指标如CC和BC能够利用整个网络结构的信息，更优地识别有影响的重要节点，但也存在一定的缺点和限制。

表1 节点重要性的最新代表性研究成果

2 节点重要性优化算法

Ferber 等人[16]通过在不同的空间，即L 空间、B 空间、P 空间和C 空间中用备选网络配置来表示系统，其中L 空间强调节点相邻功能。在L 空间中公交系统的每个站点均为一个节点，若任意两个节点是一条或多条公交线路上的连续站点，则两节点间存在链路。城市轨道交通系统可转换成未加权网络G=(V,E)，其中节点集V={vi,i=1,2,…,N}和边集E={eij,i,j=1,2,…,N,i≠j}，eij=(vi,vj)代表由两个相邻节点(i,j)组成的连接。由此，形成了一个相关的邻接矩阵A=[aij]。若节点和节点是相邻的，则aij=1，否则aij=0。本质上轨道交通基本物理结构是其日常客流运输的骨架。基于未加权网络和横断面客流，可建立有向加权网络模型Gw=(V,E),W，其中设定的权重W={wij,i,j=1,2,…,N,i≠j}，wij表示在某个时间段内相邻站点i和j之间旅行的乘客数量。

假设一个如图1 所示的网络，由3 条线和7 个节点组成，XNm=[xij],j=1,2,…,m，节点C是三线换乘站。

图1(a)表示无向和未加权图G=(V,E)，所有边均相等。实际的轨道交通系统中每个车站均存在站内和站外客流的差异，因此其将客流权重分配到每一侧的不同方向，如图1(b)所示，从而得到有向加权的轨道交通网络Gw=(V,E,W) 。为挖掘节点重要性随网络发展的演化机制，需进行不同拓扑结构的复杂网络建模。

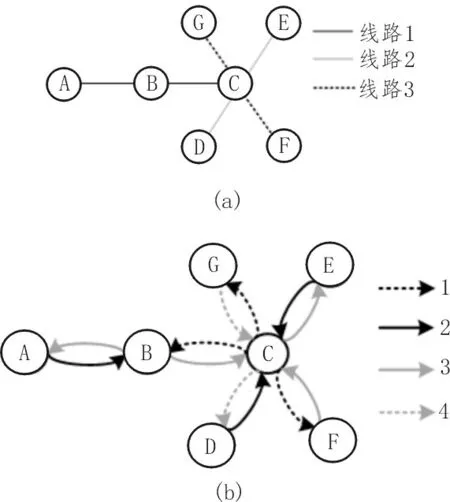
图1 三线七节点轨道交通网络示意图

3 数值分析与讨论

3.1 数据描述

以某地区的地铁为例，将上述方法应用于城市轨道交通节点重要性演化研究。该地区2016 年开通了3 条新地铁线，地铁日客流曲线在开通新线后有明显的增加。其客流包括进站、出站和换乘客流。数据由PostgreSQL 进行清理和去噪，数据集的时间范围为6:00 到24:00。开通新线意味着网络结构改变，客流重新分配。从图2 可看出，时间跨度可以根据新线路分为3 个时期，网络节点的数量分别为118、132 和166。为了深入研究网络演化过程中节点重要性的变化过程，该文从3 个跨度中选择了3 个时期进行网络建模。考虑到日常通勤，工作日的总客流量通常大于周末，所以以3 个时期的3 个周一为例进行数值分析，其分别是2016∕4∕11（时期I）、2016∕8∕8（时期II）和2016∕12∕5（时期III）。

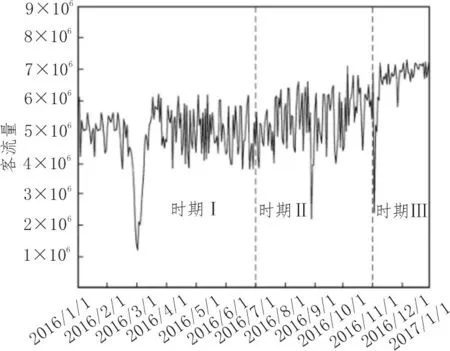
图2 某一线城市2016年日客流量曲线

3.2 网络演化中的节点中心性分析

首先，从上到下对站点进行编码，尤其是中转站需要用较小的线路编码。分别对166 个III 期站、132个II 期站和118 个I 期站完成编码后，基于3 个时期未加权和已加权的SZM 网络，采用第2 节所述的方法得到节点中心度。

节点的度可以描述其连通性，在未加权的SZM网络中，所有节点度的最小值为2。3 个时期节点度的频率分布直方图如图3 所示。其中度值为4，在3 个时期分别占82.20%、81.82%和76.51%，比例最大。这表明SZM 网络的无标度性和异质性特征更加明显，即少数中枢节点在网络运行中起主导作用。此外，上述分析结果揭示了SZM 网络的异质性。

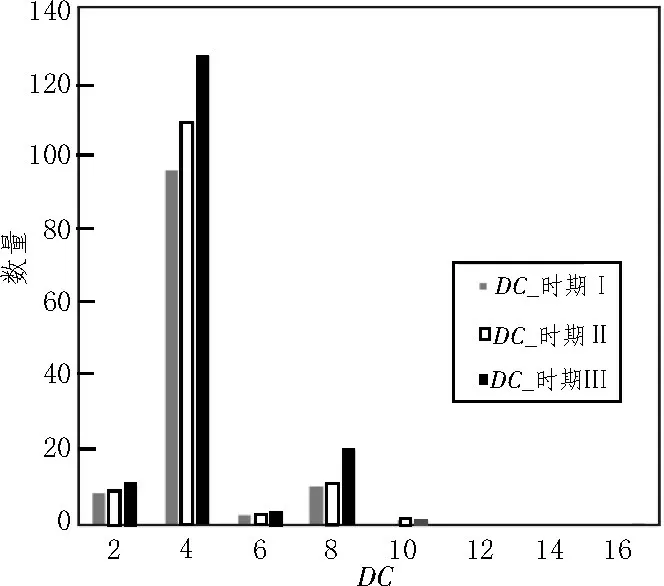
图3 3个时期内度的频率分布直方图

随着新线路的开通，SZM 物理网络平均贴近度的中心度从0.077 提高到0.092，表明节点间的贴近度增强。从图4 中所有节点的概率分布图来看，未加权网络中CC的趋势倾向于标准正态分布。而CCw的概率直方图随着时间的增加有从正态分布变为线性分布的趋势，说明加权网络中，各节点对其邻居的影响程度在客流的权重下趋于平衡。

图4 CC和CCw在3个时期内的概率分布

对于每个时期中的所有节点，一些具有较高BC的节点通常是中转站，中转站对物理网络的控制比普通中转站更强。其成为新线条的重要支点，并且通过这些节点的最短路径是最多的。从图5 中可看出，对于BC和BCw，3 个时期概率分布图的总体趋势均呈现出右长尾的正态分布。这是因为网络中有几个节点具有较高BC和BCw。简而言之，加权介数中心度更适合描述网络中节点的负载强度。

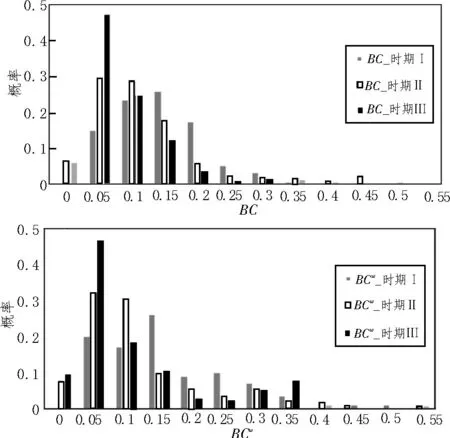
图5 BC和BCw在3个时期内的概率分布

3.3 节点重要性演化分析

动态网络中的节点重要性可基于拓扑指数测量和WTOPSIS 算法来识别。考虑到网络建模中的不同情况，节点重要性的评估指标在未加权的SZM 网络中主要包括DC、CC和BC，在加权的SZM 网络中主要包括DCw、CCw和BCw。

上文中的变异系数法用于获取指数权重Wj，结果如表2 所示。每个指标的权重值表示其在节点重要度评估中所占的比例。在这些指标中，BC权重在未加权的SZM 网络中最低，而CCw权重在加权的SZM 网络中所占的比例最小。获得权重指数Wj后，第二步是将其应用到WTOPSIS 算法中，从而可获得与理想解的相对接近值C，最终可以得到节点不同情况下的重要性排名结果。

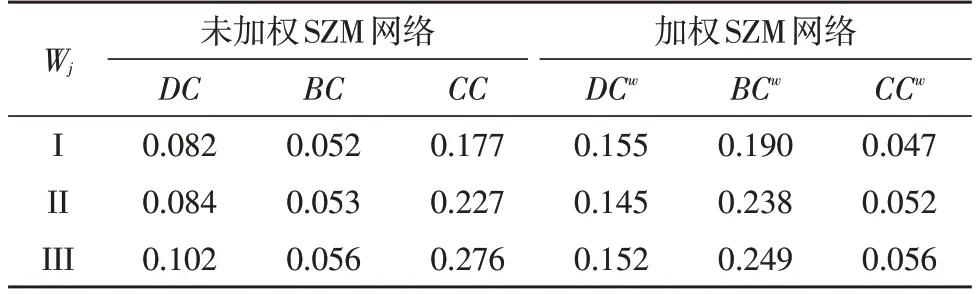
表2 不同SZM网络情况下的Wj指数权重

随着网络演进，CGM 在I 期为标准站，II 期为双线换乘站，III 期为四线换乘站，如图6 所示。其3 期排名结果分别为RankC={1 5,6,1}、={8 ,6,6}和={9 ,9,4}。相关分析表明，P值为0.022，双尾检验显著。同样对于始终客流最多的LJ 站，其拓扑结构始终是相同的。采用上述方法，若相关性分析中的显著性检验不被接受，则在这种情况下无法确定哪个因素更容易受到其加权重要性的影响。但对于XMH 站始终是一个标准站，其排名结果是RankC={1 0,7,8}、={4 ,3,3} 和={8 3,87,107}。相关性分析表明，其加权节点重要性比拓扑结构更容易受客流影响，这与CGM 相反。

图6 CGM、LJ、XMH站在3个时期的拓扑结构

简而言之，在复杂的轨道交通网络中，节点重要性演化受到拓扑复杂性、客流动态、时空特性、轨道交通城市规划等社会或政治因素的影响。对于某个车站，其不能仅根据拓扑结构或客流量来直接确定其是否重要，则需要考虑较多因素来进行全面的定性和定量评估。

4 结束语

该研究将未加权和已加权的复杂网络模型化于轨道交通网络演化中，测量出网络中每个节点的局部和全局中心度，其中包括DC、CC、BC、DCw、CCw、BCw，并提出采用WTOPSIS 算法对节点的重要性进行排序。此外，定量计算了拓扑重要性排序集、加权重要性排序集和客流量排序集之间的交集度和相关性，以评价排序结果的相似性，并在此基础上深入地讨论了影响节点重要性演化的因素。通过实例研究表明，该算法在节点重要性排序方面的性能优于现有的单属性算法。对于网络开发中的不同站点，节点重要性演化主要受拓扑结构和客流变化的影响，但程度有所不同，即对于轨道交通中的部分站点，其节点重要性的变化比客流更容易受到拓扑结构的影响，而对于其他站点则相反，这需要结合实际情况进行具体分析。该文为城市轨道交通网络发展中节点重要性的演化机制研究提供了参考，结果对城市轨道交通的网络化运营提供了理论支撑。