飞轮用永磁悬浮轴承的磁路设计及磁力解析模型
高峻泽,柳亦兵,周传迪,何海婷,武 鑫
(华北电力大学,北京 102206)
飞轮储能具有响应速度快、寿命长等特点,非常适合电力系统快速负荷调节,可以为保障新型电力系统安全稳定性发挥重要作用。磁悬浮轴承技术是高速、重载飞轮的关键技术之一[1]。磁悬浮轴承是一种利用磁场力将被支承件平稳悬浮于某一特定空间的高性能轴承,包括永磁轴承(permanent magnetic bearings,PMB)[2]、电 磁 轴 承(active magnetic bearings,AMB)[3]、超导磁轴承(superconducting magnetic bearings,SMB)[4]以及各种混合磁轴承(hybrid magnetic bearings,HMB)[5]等。永磁轴承具有成本低、体积小、无功耗等独有优势,吸引了大量学者的研究。但是由Earnshaw 定律可知[6],仅靠永磁轴承不能实现物体所有自由度的稳定悬浮,因此常常与其他磁轴承或机械轴承组合构成各式各样的混合磁悬浮轴承广泛应用于飞轮储能系统中。文献[7]设计了一款轴向由永磁轴承+陶瓷球轴承卸载的立式飞轮转子,整个飞轮转子重105 kg,飞轮转子工作在10 Pa、20000 r/min时的总能量转换效率约为78%,轴承损耗约为12%[8]。文献[9]设计的飞轮转子轴向采用永磁轴承+锥形螺旋槽轴承卸载,额定储能量为500 W·h,在12000~36000 r/min转速范围内的充放电循环效率为41%,空损与轴承损耗之和不足10%。文献[10]在相同的真空环境下进行了采用电磁轴承和永磁+电磁混合轴承卸载时放大器所需输入功率的对比实验,结果表明永磁+电磁混合轴承只需要3.59 W 的放大器输入功率,而电磁轴承需要29.6 W。虽然超导磁轴承具有无源自稳定、无需控制和低能耗的优点,吸引了大量学者的研究,但其悬浮力较小、刚度较AMB 和PMB小1~2 个数量级以及会因超导体磁通蠕变产生悬浮力弛豫现象引发系统稳定性,很难满足工程实际应用[8]。储能飞轮作为机电一体化的高速旋转机械,其上每个旋转部件都承受着极大离心载荷的作用,然而现有永磁轴承多采用动、静磁环结构,固联于转子上的动磁环部分随转子一起高速旋转,动磁环必然遇到强度不够的突出问题[11]。
近年来,随着稀土永磁材料性能的不断提升,国内外学者针对不同结构的永磁轴承进行了承载能力和静刚度的大量研究,研究方法主要有等效磁荷法[12]、分子电流法[13]、矢量磁位法[14]、虚位移法[15]和有限元法[16]等。文献[17-21]对双环、多环和Halbach阵列结构的永磁轴承进行了磁力解析模型的研究。
在已知磁路结构形式的前提下,采用有限元法设计磁路需要通过试凑来选取满足设计要求的尺寸参数,耗时较长,而且往往不能得到可充分发挥磁能的合适的磁路参数。因此,本文针对单环吸力型永磁轴承结构,以获取合理磁路参数为目标,通过磁路设计与计算,建立了适用于高转速、大承载飞轮转子的永磁轴承的承载特性解析模型,最后利用ANSOFT Maxwell有限元分析软件对模型合理性进行了验证。
1 飞轮储能结构及永磁轴承工作原理
1.1 飞轮储能结构
考虑一种如图1 所示飞轮储能转子基本结构,其双向电机转子布置在飞轮转子上方,转子径向由上下端电磁轴承支撑,轴向由电磁+永磁轴承共同支撑,保持飞轮转子稳定悬浮,其中吸力式轴向永磁轴承承担飞轮转子重量的主要部分,采用单环结构;轴向电磁轴承承担飞轮转子重量的其余部分以及抵御外界干扰力。

图1 飞轮储能系统结构(永磁轴承与壳体固联)Fig.1 Flywheel energy storage system structure(permanent magnet bearing is fixedly connected with shell)
1.2 轴向永磁轴承结构及工作原理
单环吸力型轴向永磁轴承根据永磁环与磁轭的位置关系有3种不同结构(图2),本文以图2(a)永磁环外置式结构为例,说明永磁轴承的工作原理以及承载力和静刚度解析模型的建立。

图2 单环轴向永磁轴承3种不同结构Fig.2 Three different structures of single ring axial permanent magnet bearings
图2中(a)永磁环外置式结构形式的轴向永磁轴承系统工作原理及具体结构尺寸如图3所示。图中竖线阴影部分为轴向磁化的环状永磁体,用来产生磁通,磁轭和转子均为软磁材料。磁路经过永磁体、磁轭、气隙1、转子、气隙2 形成闭合主磁通回路,轴向承载力由主气隙磁通(气隙1 和气隙2)产生。

图3 单环吸力型轴向永磁轴承Fig.3 Single-ring suction axial permanent magnet bearing
2 永磁轴承磁路分析及解析模型建立
2.1 磁路分析及结构参数的确定
由基尔霍夫第一定律(即磁通连续原理),有

式中,Lg为轴向间隙。
另外,由结构几何关系有

其他结构参数确定为

至此,轴向永磁轴承所有结构参数均已确定。
2.2 考虑边缘效应的等效磁路模型
根据轴向永磁轴承结构,建立等效磁路模型,在此之前做出如下合理的假设:
(1)磁轭上表面完全用磁绝缘材料覆盖,不考虑磁轭上方的漏磁;
(2)将磁轭作为良性导磁材料,即其磁导率比空气大得多,忽略其磁阻;
(3)由于工作气隙较小,近似认为气隙处磁场均匀。
磁场分割法的实质是用理想化了的磁力线将整个极间气隙磁场分割为若干个具有规则形状的磁通管,求出它们的磁导后,再根据其串并联关系得到整个气隙的磁导。这种方法适应性强,可以满足磁极形状复杂或者虽不复杂但必须考虑边缘扩散效应时的磁场分析。只要根据磁力线规律正确分割磁场,并选择合适的计算公式,计算结果的准确度一般可以满足工程计算要求[23]。
假设转子产生轴向位移z,则根据磁场分布情况,利用磁场分割法将气隙磁场及边缘扩散磁通划分为以下7个磁通管(图4):

图4 磁场区域分割Fig.4 Magnetic field region segmentation
(1)磁通管1——磁轭正下方的圆筒状磁通管;
(2)磁通管2——环形永磁体正下方的圆筒状磁通管;
(3)磁通管3——磁轭内侧与转子轴肩外侧之间的圆筒状磁通管;
(4)磁通管4——环形永磁体内侧的漏磁磁通管,视为半径为h1的1/4圆截面旋转体;
(5)磁通管5——环形永磁体外侧的漏磁磁通管,视为半弓形截面旋转体;
(6)磁通管6——磁轭外侧扩散磁通管的第Ⅰ部分,视为半径为h3的1/4圆截面旋转体;
(7)磁通管7——磁轭外侧扩散磁通管的第Ⅱ部分,视为1/4 圆截面与半弓形截面旋转体之差,可近似视为1/4圆环截面旋转体。
各部分磁导分别记为G1~G7,具体表达式为

根据各部分磁导之间的串并联关系,建立对应的磁路模型,如图5(a)所示。
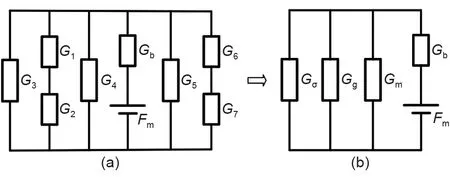
图5 (a)等效磁路模型及(b)简化模型Fig.5 (a)Equivalent magnetic circuit model and(b)simplified model
图中,Fm、Gb分别代表永磁体的总磁动势和内阻磁导;Gg代表气隙总磁导;Gm代表永磁体内、外侧漏磁总磁导;Gσ代表磁轭内、外侧散磁总磁导。
根据磁导串并联关系,合并同类型磁导,将磁路模型进行简化,简化后模型如图5(b)所示。
气隙总磁导Gg、漏磁总磁导Gσ以及散磁总磁导Gm分别为

2.3 磁路的总磁通


图6 NdFeB永磁体退磁曲线及磁路工作负载曲线Fig.6 Demagnetization curve and magnetic circuit working load curve of NdFeB

式中,Br、Hc、Lm、Sm均为已知参量,漏磁系数σ和总磁导G可通过2.2小节磁路分析求得。
2.4 轴向承载力和刚度解析模型
根据电磁场理论,气隙磁场能表达式为

以上轴向永磁轴承的磁路设计及承载力和静刚度模型的建立可以描述为图7所示的流程。

图7 轴向永磁轴承设计流程Fig.7 Design flow of axial permanent magnet bearing
3 解析计算示例
按照图7所示的磁路设计流程,进行一种永磁轴承磁路设计。设转子和永磁轴承取表1 所列材料,当轴向间隙为1 mm时,轴向永磁轴承需承担800 N的转子重量,通过计算得出系统的结构参数列于表2。

表1 转子和永磁轴承材料Table 1 Rotor and permanent magnet bearing materials
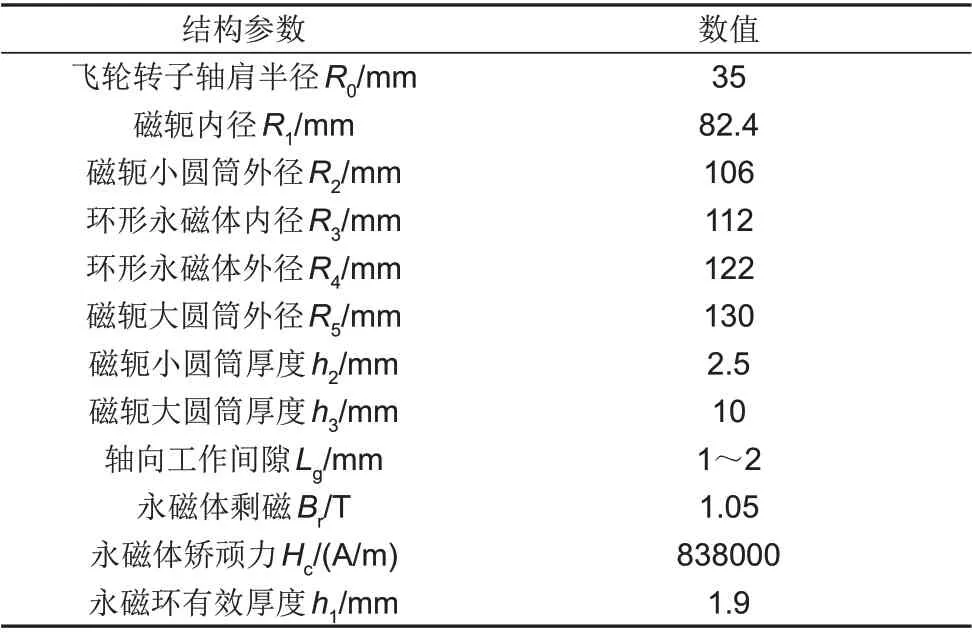
表2 永磁轴承结构参数Table 2 Structural parameters of permanent magnet bearings
根据图7磁路设计流程,计算得到永磁轴承轴向承载力和轴向静刚度随轴向间隙变化的曲线,如图8所示。可以看出,随轴向间隙的增大,轴向承载力逐渐减小,而轴向静刚度逐渐增大。
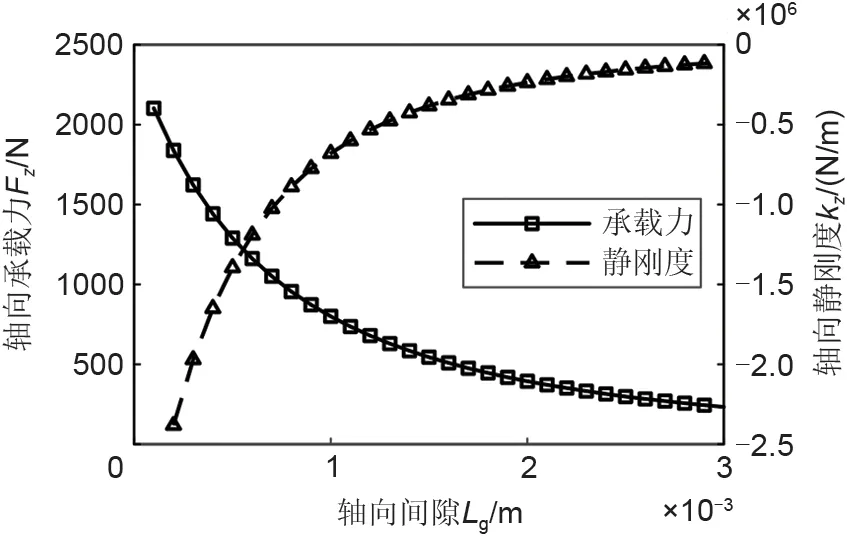
图8 轴向承载力与静刚度随轴向间隙变化的曲线Fig.8 Curve of axial bearing capacity and static stiffness changing with axial clearance
4 结果验证
目前,主要采用试验法和有限元法对永磁磁场进行验证[19],而具有验证便捷、成本低廉、精度较高等优点的有限元法已被广泛应用于永磁轴承磁路设计的验证计算中[24-25]。因此本文采用有限元方法对上述磁路设计结果进行验证。
由于飞轮转子及永磁轴承均为旋转轴对称结构,在只讨论轴向承载特性的前提下,可以采用简化的二维模型进行有限元分析。建立x-z二维坐标系,x、z分别代表径向和轴向,根据表2 结构参数建立单环吸力型轴向永磁轴承有限元模型,按照表1定义各部件材料,将求解域设为真空。计算得到轴向间隙Lg=1 mm时的磁力线分布和磁感应强度分布云图分别如图9 和图10 所示,通过解析模型(图4)与有限元计算得到的磁力线分布对比,可以看出,除了忽略掉的磁轭上方位置处少许漏磁外,其余部分的磁场分布基本一致;另外,从磁感应强度云图上可以看出,漏磁对整体磁场影响较小,可忽略不计。因此认为解析模型中对磁场区域的分割是比较合理的。
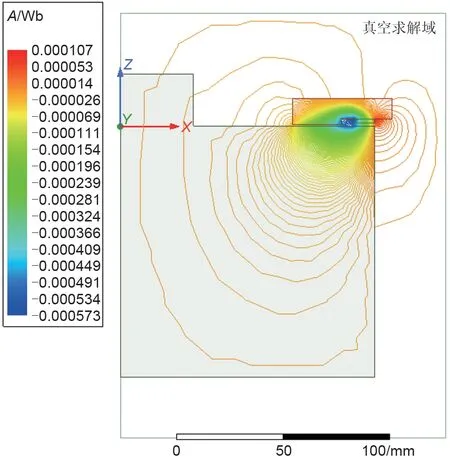
图9 Lg=1 mm时的磁力线分布Fig.9 Magnetic line distribution(Lg=1 mm)

图10 Lg=1 mm时的磁感应强度云图Fig.10 Magnetic induction intensity nephogram(Lg=1 mm)
根据所建立的有限元模型,计算得到永磁轴承的轴向承载力和静刚度(由于轴向静刚度为负刚度,此处只取其数值绘图)如图11 所示。图中同时给出解析模型的计算结果以及两种计算的相对误差。可以看出,轴向间隙在0~3 mm 范围内,仿真结果与解析结果的轴向承载力吻合良好,最大相对误差为8.7%;轴向静刚度趋势相符,相对误差稳定在10%左右,验证了解析模型的合理性。下面分析在不同的轴向间隙范围内,仿真结果与解析结果的主要特点和误差来源。

图11 轴向承载力和静刚度随轴向间隙变化的曲线Fig.11 Curve of axial bearing capacity and static stiffness changing with axial clearance
(1)在工作间隙(1~2 mm)范围内,轴向承载力的解析结果和仿真结果吻合非常良好,最小相对误差为0.58%,最大相对误差为2.5%;轴向静刚度的两种计算结果趋势相符,满足设计要求。
(2)在较小间隙(0~1 mm)范围内,轴向承载力和轴向静刚度的解析结果在数值上均小于仿真结果,主要原因是在对磁场区域分割时(图4),忽略了磁轭外环侧面的远端磁力线(磁通管6和7之外),使得磁轭外侧磁极气隙磁导[式(40)]的计算结果偏大,进而造成气隙磁场能[式(49)]的计算结果偏小,最终导致轴向承载力以及轴向静刚度的解析计算结果在数值上偏小。
(3)在较大间隙(2~3 mm)范围内,轴向承载力的解析结果大于仿真结果,而轴向静刚度的解析结果在数值上小于仿真结果,主要原因是在建立解析模型时,忽略了磁轭上表面的漏磁以及假设气隙1、气隙2 磁场均匀分布使得漏磁导[式(36)]的计算结果偏小,引起总磁导[式(38)]的计算结果偏大,导致气隙磁通[式(47)]的计算结果偏大,最终表现为轴向承载力以及轴向静刚度的解析计算结果在数值上偏大。
5 结 论
针对立式飞轮转子的3 种不同结构形式的单环吸力型轴向永磁轴承布置方案,以其中永磁体外置式结构为例建立了轴向承载力和轴向静刚度的解析模型,基于传统磁路设计方法进行了磁路设计计算,并通过有限元分析进行了验证,得出以下结论:
(1)随着轴向间隙的增大,轴向永磁轴承的轴向承载力逐渐减小,而它的轴向静刚度逐渐增大,且二者变化速率均逐渐趋于平缓。
(2)建立的解析模型与有限元模型计算结果较为吻合,在设定的工作间隙范围内,相对误差最大不超过2.5%,可以获得较好的计算精度。
(3)提出的磁路设计方案以及承载特性计算模型可以为立式飞轮转子永磁轴承结构的初步设计和参数确定提供一种简洁快速的计算工具。

