用RMI原理与仿射变换解决椭圆问题

陈 倩

(江苏省扬州大学数学科学学院，225002)

一、RMI原理简介

RMI原理是我国数学家徐利治教授提出的一种处理问题的普遍方法或准则,即关系(Relation)、映射(Mapping)、反演(Inversion)原则.具体表述为:它通过某种映射φ,将一个较为复杂的系统S(原象系统)映射为一个新的简单的系统S*(映射系统),在新系统S*中处理好对应关系并得到问题的解x*,再通过逆映射φ-1反演到原问题的解x.

二、RMI原理在椭圆问题中的映射途径分析

就椭圆问题而言,可以利用RMI原理将椭圆问题映射为圆的问题进行讨论,进而借助圆中良好的几何性质解题,达到化繁为简、事半功倍的效果.

(4)共线三点在变换前后保持共线关系不变,且共线的线段长度之比不变.

总之,在RMI原理下利用仿射变换解决椭圆问题,其一般模式如图1所示.

图1

三、应用举例

(1)求C的方程,并说明C是什么曲线;

(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.

(i)证明:∆PQG是直角三角形;

(ii)略.

评注本题第(2)问通过仿射变换φ1,将椭圆的内接三角形问题转化到辅助圆中,借助象点P′,Q′关于原点对称及P′Q′为圆的直径,根据直径所对的圆周角为直角,利用斜率轻松获得kP′Q′kP′G′=-2(定值),最后由仿射变换关于斜率的结论反馈到椭圆中,使问题顺利获证.

例2(2008年全国高考题)设椭圆中心在坐标原点O,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于点E,F两点.

(2)求四边形AEBF面积的最大值.

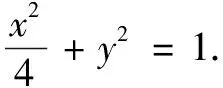
评注本题通过仿射变换φ2,将椭圆的内接三角形问题转化到辅助圆中，根据相交弦定理及定比分点公式得到象点D′的坐标和对应的斜率kOD′,根据三角函数的有界性对像四边形A′E′B′F′的面积进行估值,最后由仿射变换关于斜率和面积的结论反馈到椭圆中,避免了椭圆中繁琐的计算,发挥了平面几何知识与三角函数知识应有的作用,方便了解题.

(1)求椭圆C的方程;

(2)设P是椭圆C上的一动点,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:|AN||BM|为定值.

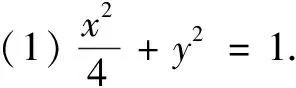
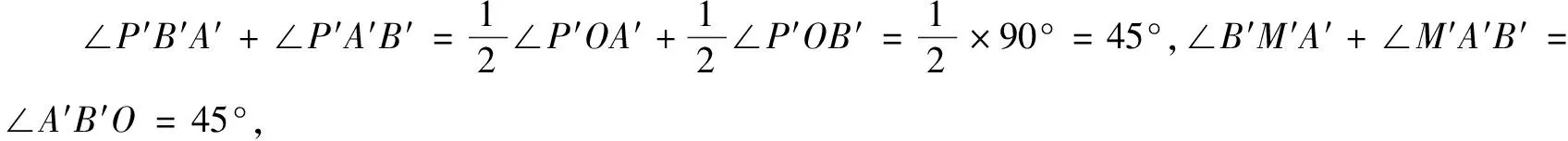
当点P位于第二、三、四象限时,同理可得|A′N′||B′M′|=|A′B′|2=8(定值).

由|A′N′||B′M′|=8,结合仿射变换中关于弦长的结论,得|AN|·2|BM|=8,即|AN||BM|=4为定值.

评注本题通过仿射变换φ3,将椭圆的内接三角形问题转化到辅助圆中,利用圆周角与圆心角的关系及相似三角形的知识得到|A′N′||B′M′|为定值8.显示了平面几何知识强大的威力,为后续利用仿射变换的性质反馈到椭圆中使问题获解做好了铺垫；表明了使用RMI原理解题可以沟通不同知识模块之间的内在联系,有效提高解题的灵活性.

四、感悟与总结

与椭圆相关的问题一直是近年来高考试题中的热点问题,通过上面几个例题,我们可以体会到将RMI原理与仿射变换结合起来对于解决椭圆问题的妙处,利用RMI原理和仿射变换将椭圆问题转化为圆的问题,结合圆的优美性质求解相应的问题,这不仅大大地降低了运算量,也在一定程度上拓宽了研究问题的视野,由此可见数学思想与解题技巧的重要性.