实施降幂策略 优化问题化归

姚星桃

(江苏省扬州市职业大学数学科学学院,225000)

化归是一种数学思想方法,是一种思维方式,在学习心理学意义下,化归又是一种学习活动.姬梁飞在文[1]中指出:化归是由目标、对象、性质、特征、方法等要素构成,联系、变维、映射及类化是化归的四大特征,其中“降维”是化归的核心[1]. 这里“降维”就是将复杂问题转为为简单问题的方法,如三角函数中的降幂、解方程中的消元、空间几何问题平面化,利用同解变形化三角方程、指数方程和对数方程为简单方程等.特殊地,将高次的问题化归为较低次的类似问题来研究称为降幂.降幂在解题中有着广泛的应用.本文探讨一些降幂方法,研究其在化归解题中的作用.

一、巧用降幂方法

降幂是化归解题过程中的核心,灵活运用这种降幂的方法解题,则能收到满意的效果.

1.使用公式降幂

分析直接利用降幂公式,结合诱导公式加以转化,就能顺利解题.

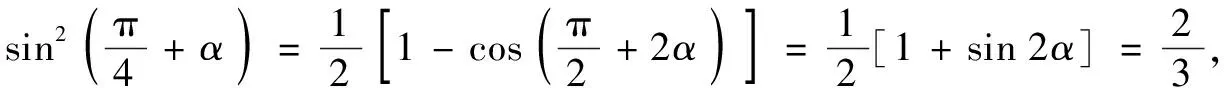
变式1(1995年全国高考题)求sin220°+cos250°+sin 20°cos 50°的值.

分析本题虽然可以采用构造法、几何法等方法求解,但都相对复杂,而利用降幂公式和积化和差公式可迎刃而解.

分析从条件和结论之间的差异看,本题可通过平方关系及降幂公式将其降幂且倍角,得到解题的目的.

2.用变量代换降幂

化归起始于联系,这种联系存在于数学对象内部或不同数学对象之间,在一定条件下可以相互转化.化归的实现必须将研究问题予以分解、重组及类化,要具有丰富的联想,善于发掘事物内外的联系,寻找与其相关的元素或曾经解决过的类似问题.

例2关于x的方程x4+ax3+ax2+ax+1=0有实根,则实数a的取值范围是______.

评注本题在求解过程中,有意识地建立引参代换是一种整体转化的思想,也是实现降幂的关键.由题目中已知条件的结构来确定变量代换的形式是需要在解题过程中灵活处理的.下面的问题原式不易化简,而解方程后代入求解又不可取,可运用逐步代换进行降幂化简,使求值能轻松获解.

3.选择主元降幂

所谓主元法,是在解决多元问题时,以其中一个变元为“主元”,而将其他变元视为常量的解题策略.

2）从学习内容来看，具有开放性、整合性。主题学习有异于传统的以教材为中心的学习，学习内容可根据实际情况灵活选择，涉及多学科、多领域，不必按照传统的课本教材。

例5已知-1≤m≤1,函数f(x)=x2+(m-4)x+4-2m的值恒大于零,求x的取值范围.

分析若视m为主元,则x2+(m-4)x+4-2m是关于m的一次函数.由一次函数的单调性可快捷地确定x的取值范围.

解以m为主元,则原函数可改写为关于m的一次函数g(m)=(x-2)m+x2-4x+4.依题意,要g(m)在-1≤m≤1时恒大于零,只需g(-1)>0,g(1)>0.

由g(-1)=x2-5x+6>0,解得x<2或x>3;由g(1)=x2-3x+2>0,解得x<1或x>2.

综上,所求x的取值范围是(-∞,1)∪(3,+∞).

二、运用降幂思维

化归思想的应用归根结底是体现解决问题过程中所拥有的一种数学思维意识,自觉地应用联系、运动、发展的眼光观察问题、分析问题,利用事物运动规律对复杂抽象问题向简单方向予以转化,这就是降维思维,它能引导解题的方向和策略的选择.

例6若正数a,b,c同时为一个等差数列和一个等比数列的第m,n,k项,求证:(b-c)lga+(c-a)lgb+(a-b)lgc=0.

分析若等比数列的公比q=1,则a=b=c,则结论显然成立.

下面的证明过程中假设q≠1.设题中的等差数列为{bn},bm=a,bn=b,bk=c,由等差数列的性质,可得

(m-n)d=bm-bn=a-b,

①

(n-k)d=bn-bk=b-c,

②

(k-m)d=bk-bm=c-a.

③

设题中的等比数列为{an},am=a,an=b,ak=c,由等比数列的性质,可得

④

⑤

⑥

接下来就是通过计算来证明结论的正确性,但这一步却是大多数学生理不出头绪、容易算错的一步.为了解决这类问题,仔细观察①～⑥ 几个等式,并联系待证结论,需要把④ ⑤ ⑥ 中幂指数 “降”下来,转化到①～③ 式.不难发现,取对数转化是最佳选择,事半功倍.于是把上述指数式化为对数式,得

由此结合①～③ 式,可得

将此三式相加,就可以得到要证明的等式.

评注本题中出现了带参数的幂的运算,证明时采取了把指数式④ ⑤ ⑥ 化为对数式的方法,有效简化了计算.这里降幂意识是取对数转化，迅速化解了计算遇到的困难.英国数学家纳皮尔通过化归法解决了数学领域的运算问题,将复杂的乘方开方运算问题转换为简单的加减与倍积问题,实现了计算方法的一次革命[2].这种思维方式被经常地应用到问题解决中.

2.最值问题借力降幂不等式策略

例7已知x,y,z>0,且x+y+z=1,求P=x2+3y2+z3的最小值.

分析这类题可用拉格朗日乘数法求解,但此解法在大学数学中才介绍.如果用初等的方法求解,由于求最值的表达式三个被加项的系数不同,次数也不等,使基本不等式用不上,给求解带来困难.对x2,3y2,z3三项,灵活选择t,则可使问题获得简捷明快的解决.

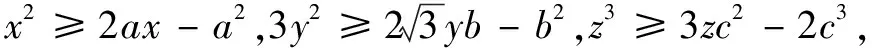
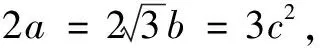
评注降幂放缩法在在讨论含指数式的不等式中具有高效快速特点.

史宁中教授认为,模式是认识、表达、解决一类数学问题的程式化了的方法[3].化归是数学活动中普遍应用的一个基本思想方法,有利于发展学生数学学科核心素养.无论是从空间到平面、从数字到图形、从曲线到直线、从无限到有限、从特殊到一般、从杂乱到有序、从抽象到具体、从现象到模型,“降维”是实施化归的核心,对探究数学对象之间的关联、优化问题解决尤其重要,需要高度关注.